低雷诺数下凹坑结构对翼型层流分离影响的数值研究

焦雪文，张立茹，2，3，牛佳佳，汪建文，2，3

（1.内蒙古工业大学 能源与动力工程学院，内蒙古 呼和浩特 010051；2.风能太阳能利用技术教育部重点实验室（内蒙古工业大学），内蒙古 呼和浩特 010051；3.内蒙古自治区风能太阳能利用机理及优化重点实验室（内蒙古工业大学），内蒙古 呼和浩特 010051）

0 引言

小型风力机工作在雷诺数Re较低的工况下，低Re下的翼型绕流流场十分复杂，翼型表面流体会经历分离、转捩、再附着等非定常过程。由于Re较低，翼型表面大部分区域为层流状态，包含的能量较少，不足以抵抗较大的阻力。在逆压梯度和摩擦阻力的双重作用下，翼型表面流体的流速逐渐减小到零，之后流体开始离开翼型表面，形成开式分离区域或闭式分离泡[1]。分离现象不仅影响翼型的气动性能，还会引起振动，造成叶片的损坏。因此，从改善翼型气动性能和提高叶片结构安全的角度来看，对低Re下出现的层流分离现象进行研究并有效地控制具有重要的意义。

关于低Re下翼型的气动性能，学者已进行了大量研究。研究方法主要有风洞PIV实验和数值计算。在低Re工况下，翼型的气动性能对攻角、Re、湍流强度等因素均特别敏感。湍流强度的增加将会使分离延迟并提前触发转捩和随后的再附着，缩短层流分离区域[2]。分离点处层流分离泡的厚度很薄，因此对实验设备分辨率的要求非常高，PIV空间分辨率和采样频率的不足会造成不同实验结果之间分离泡结构的差异[3]。所以不同风洞的湍流强度和设备分辨率及采样频率等因素，均会对实验结果产生影响。随着计算机技术的发展，数值计算的能力显著提高，一些学者采用大涡模拟（LES）方法对低Re工况下翼型的气动特性进行了研究，捕捉到了长分离泡结构，验证了LES可以很好地处理低Re工况中出现的层流分离及转捩现象[4]，LES也能够预测低Re工况下翼型的层流分离、转捩和再附着发生的位置[5]。

在低Re工况下，层流分离泡使翼型等效弯度减小、翼型压差阻力大幅度增加，造成升力系数的骤降[6]。为改善翼型气动性能，就必须对流动分离现象进行控制，降低层流分离泡带来的影响。目前，控制方法主要有增加激励器或抽吸装置等设备，以及布置沟槽及脊状等表面微结构、涡流发生器、凹凸前缘、结节等耦合仿生结构等[7]。增加设备将增加风力机的安装难度并提高风力机的运行成本，所以被动控制得到了广泛的运用。凹坑结构最早应用于高尔夫球表面，以减小流体分离和尾流效应，使高尔夫球飞行距离延长。如今，凹坑结构已经应用于强化换热[8]、平板减阻[9]等方面，并取得了良好效果。在NACA-16012翼型的水洞实验中发现，在一定深径比h/d下，凹坑结构有较好的减阻效果[10]。数值研究中，在等Re、凹坑结构参数固定不变的情况下，NACA 642-014A翼型中后部布置凹坑结构可以减小边界层的分离，但是导致了叶片气动性能的下降[11]。

在低Re工况下，凹坑结构对翼型层流分离有何影响，不同h/d的作用效果是否相同，又将如何影响翼型的气动性能等问题还尚未明确。鉴于前文所述，在低Re工况下通过实验的方法研究翼型的气动性能存在一定的困难。因此，本文采用LES的方法，对光滑翼型与布置了不同h/d凹坑结构的翼型，在Re为5×104（基于弦长）时的非定常流场进行数值研究。分析低Re下翼型表面的层流分离现象和凹坑结构及不同h/d对层流分离的作用效果，进而从压力系数、摩擦阻力系数等气动参数角度研究凹坑结构及不同h/d对翼型气动性能的影响。

1 模型及网格划分

1.1 翼型模型

本文计算翼型弦长c为0.095 7 m，展长为0.5c的NACA4415光滑翼型及在光滑翼型布置了不同h/d凹坑结构的翼型。三排凹坑结构的展向间距为0.01 m，流向间距为0.005 m。图1所示为光滑翼型及凹坑结构翼型的模型。

图1 光滑翼型及凹坑结构翼型模型Fig.1 Smooth airfoil and dimples structure airfoil model

1.2 计算域边界条件与网格划分

图2 计算域、光滑翼型与凹坑结构翼型网格Fig.2 Computational domain，smooth airfoil and dimples structure airfoil grid

计算域为长方体，距离翼型前缘上游为10c的壁面与距离翼型上、下表面为5c的壁面为计算域的入口，设置为速度入口边界条件，主流速度为8 m/s。本 文 以 攻 角AOA为4°，Re为5×104为 例，研究低Re、小AOA工况下翼型表面的流动现象。出口为压力出口，位于翼型前缘下游10c的位置。沿翼型展向的两个壁面设置为对称边界条件，壁面的距离为0.5c，翼型表面为无滑移壁面。利用ICEM模块对整个计算域进行网格划分，光滑翼型模型的网格总数为198万，凹坑结构翼型的网格总数为200万。第一层网格高度满足y+≤1，法向增长率为1.05。计算域、光滑翼型和凹坑结构翼型网格如图2所示。

2 数值计算方法

2.1 LES控制方程

大涡模拟的控制方程[12]为

Smagorinsky-Lilly亚格子模型为

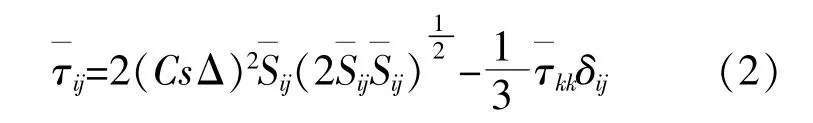
2.2 数值计算方法

本文忽略流体压缩性。由于非稳态计算与流场的初始值密切相关，在计算中首先采用k-ω SST模型对翼型绕流的稳态流场进行计算，收敛后开启非稳态计算。亚格子模型选用Smagorinsky-Lilly，速度、压力均采用二阶精度。

3 数值验证

为验证数值计算的可靠性，采用LES方法对AOA为0°，Re为5×104的NACA4415光 滑 翼 型进行非稳态计算，将时均压力系数计算结果与profili在同工况下的压力系数结果对比（图3）。由图3可知，两种压力系数分布出现平台的位置相同，发生在x/c为0.40附近，且与文献[13]所得结果一致。表明本文采用的计算方法可以准确地捕捉到翼型表面发生流动分离的位置。数值计算结果与profili所得结果吻合度较好，所以本文的数值计算结果是可信的。

图3 0°攻角下翼型表面时均压力系数对比Fig.3 Comparison of time-averaged pressure coefficient of airfoil surface at 0 ° angle of attack

4 结果分析

4.1 低Re下光滑翼型层流分离现象

选取AOA为4°，Re为5×104的光滑翼型的时均流线图，分析低Re工况下光滑翼型表面形成的分离泡及流动分离发生的位置，光滑翼型时均流线如图4所示。由图4可知：光滑翼型在上表面x为0.04 m处，即x/c约为0.40的位置，边界层开始卷起发生分离，形成后缘层流分离泡，此位置为光滑翼型层流分离点；层流分离发生后一直保持分离状态，到翼型尾缘未发生再附现象，形成了典型的开式分离泡。

图4 光滑翼型时均流线图Fig.4 Smooth airfoil time-averaged streamline

为探究凹坑结构及不同h/d对翼型表面流体流动的影响，将凹坑结构布置于层流分离点的附近。因此，本文将h/d分别为0.10，0.15，0.25的凹坑结构，布置在0.3c～0.4c的位置。

4.2 凹坑结构对层流分离现象的影响

凹坑结构翼型的时均流线图如图5所示。对比图4可知：凹坑结构翼型表面的分离流更加贴近壁面；h/d为0.10的凹坑结构翼型在x/c为0.40～0.70处形成了分离泡；h/d为0.15，0.25的凹坑结构翼型并未出现明显的涡结构，但在尾缘附近存在回流；凹坑结构翼型均没有出现大尺度分离泡。因此，凹坑结构的存在有效地抑制了层流流动分离，减小了分离的强度和厚度。

图5 不同h/d的凹坑结构翼型时均流线Fig.5 Time-average flow line of pit structure airfoil with different depth to diameter ratio

图6为光滑翼型与凹坑结构翼型的展向瞬时涡量云图。由图6可知：在前缘光滑翼型表面流体紧贴翼型表面流动，是稳定的条带状流动，但在中后部开始卷起形成涡，并随着向下游发展逐渐离开翼型表面；由于凹坑结构抑制了层流分离现象，因此，凹坑结构翼型在尾缘附近的涡旋明显减少，分离流更加平稳且贴近壁面流动。

图6 展向瞬时涡量云图Fig.6 Instantaneous spanwise vorticity contour

为深入分析凹坑结构及h/d对翼型表面流体流动状态的影响，绘出了光滑翼型及凹坑结构翼型表面在各弦向位置处的法向时均速度分布的对比曲线（图7）。由图7可知：凹坑结构对翼型前缘的速度分布几乎没有影响（x/c为0.15）；在布置有凹坑结构的弦向位置 （x/c分别为0.30，0.35和0.40）处，由于在凹坑结构内部形成了顺时针的涡结构，与主流方向相反，导致速度梯度为负；当x/c为0.40时，光滑翼型近壁面速度Ux/U＜0，表明翼型表面流体不能继续克服逆压梯度，表面的流速与主流方向相反，表面流体发生回流，出现“拐点”；光滑翼型在之后的弦向位置，近壁面速度Ux/U＜0，均存在回流现象，表明分离的流体未再附着于翼型；不同h/d的凹坑结构翼型在x/c为0.45之后的弦向位置也存在回流，但与光滑翼型相比，回流强度及分离厚度均减小；当x/c大于0.55时，不同h/d的凹坑结构翼型比光滑翼型近壁面速度Ux/U的比值更大，表示流体流速更大、包含的能量更多，可以削弱甚至抑制翼型尾缘发生分离；在翼型尾缘附近的弦向位置，h/d为0.25处的凹坑结构翼型近壁面速度最大，能够抵御更大的逆压梯度。

图7 时均速度分布Fig.7 Time average velocity distribution

4.3 凹坑结构对翼型气动性能的影响

由上文分析可知，凹坑结构及不同h/d会对流动分离产生不同的影响，对翼型的气动性能也会产生不同的影响。因此，本节从时均压力系数Cp、摩擦阻力系数Cf及统计周期内的升、阻力系数的角度进行分析。

图8为翼型的Cp，Cf分布曲线。Cp和Cf能够反映翼型表面发生流动分离、转捩及再附着的位置。在顺压梯度的作用下，翼型前缘流体流速先增加，随后在逆压梯度和摩擦阻力的双重作用下流速逐渐减小到零。由于层流动量较低，不足以抵抗更大的阻力，流体开始离开翼型表面发生分离。边界层发生分离后，流体不再减速增压，因此可以看到“压力平台”的出现。从图8（a）可以看出，光滑翼型在x/c为0.40时开始出现“压力平台”，但之后分离流并未再附着，所以Cp变化平缓。而不同h/d的凹坑结构翼型并没有明显的“平台”出现，表明出现分离的区域减少。

一般认为Cf为零的位置为翼型表面流体发生分离和再附着的位置，Cf突然增大的位置为流体由层流向湍流过渡，即转捩位置[14]。由图8（b）可知：当x/c为0.40时，光滑翼型表面的摩擦阻力系数曲线与Cf=0的直线相交，表明层流分离发生在x/c为0.40附近；当x/c为0.60时，Cf增大，分离的流体可能在空中发生转捩；在x/c为0.40的位置之后，光滑翼型便一直处于分离状态；不同h/d的凹坑结构翼型在x/c为0.45附近的位置存在分离，而在尾缘的Cf高于光滑翼型，且部分位置Cf曲线位于Cf=0的直线的上方，表明凹坑结构翼型在尾缘的分离区域减小，分离强度降低。基于边界层理论，转捩后的湍流与外部主流剧烈掺混，将裹挟主流更多的能量并与低能流体进行交换，当表面低能流体的能量增加到能够抵御逆压梯度和摩擦阻力时，分离的流体将会再附着于翼型表面，否则将一直处于分离状态。在本文计算工况下，在光滑翼型发生转捩之后，其壁面Cf一直位于y=0直线的下方，表明转捩后的流体没有发生再附着，一直处于分离状态。不同h/d的凹坑结构翼型在布置凹坑结构的起始位置（0.3c～0.4c）便与Cf=0的直线相交，但并不是发生了流动分离，而是在凹坑结构内部形成了顺时针方向的漩涡，导致速度梯度为负而表现出摩擦阻力系数小于零。

图9 升、阻力系数随时间变化曲线Fig.9 Change curves of CL and Cd coefficient with time

图9为光滑翼型及不同h/d下的凹坑结构翼型在采样时间内的升力系数CL和阻力系数Cd随时间的变化曲线。由图9可知，光滑翼型的平均CL明显低于凹坑结构翼型，而平均Cd却较高。表明在本文所计算工况下，凹坑结构具有增升减阻、改善翼型气动性能的作用。统计了在光滑翼型5个CL变化周期内升、阻力的数据，进行时间平均。结果表明：当凹坑结构的h/d为0.25时，平均CL增加了11.16%，Cd降低了19.89%，升阻比最大CL/Cd为18.23；光滑翼型的CL和Cd除了出现小波动外，还出现了周期性的大波动，而凹坑结构翼型的波动则较小，这是因为凹坑结构的存在抑制了层流分离，翼型尾缘的脱落涡明显减少，所以无剧烈波动的特点。

5 结论

本文首先对低Re下光滑的NACA4415翼型的层流分离现象进行了研究，然后采用在光滑翼型表面布置凹坑结构的被动控制方法，分析了凹坑结构在低Re工况下对层流分离现象的影响及不同h/d对其的控制效果，得到以下结论。

①光滑翼型在x/c为0.40附近开始形成层流分离，布置了凹坑结构使分离流更加贴近翼型表面，减小了分离的强度和厚度，且凹坑结构翼型尾缘附近的分离涡明显减少，与光滑翼型相比，凹坑结构翼型的近壁面速度增大，对层流分离起到了很好的抑制作用。随着h/d的增加，近壁面速度也在增加，因此能够抵御更大的逆压梯度。

②在低Re下，凹坑结构具有增升减阻、改善翼型气动性能的作用。布置有凹坑结构的翼型的升、阻力系数无剧烈波动，当h/d为0.25时，平均CL增加了11.16%，Cd降低了19.89%，平均升、阻力系数比值达到最大值18.23。