交变温度场对光伏组件性能的影响研究

孟 炎，高德东，铁成梁，叶 军，王 珊

（1.青海大学 机械工程学院，青海 西宁 810016；2.青海大学 发展规划处，青海 西宁 810016）

0 引言

光伏组件作为光伏电站的核心部件，其效率、功率衰减性和可靠性直接影响光伏电站的投资回报及整个光伏行业的发展前景[1]。光伏组件的发电能力受环境因素影响很大，不同使用条件下组件展现不同的性能[2]。就青海省而言，辐照度强、日照时间长和广阔的土地资源为当地光伏产业的发展提供了优越的地理条件，其中柴达木盆地年日照时数为3 200～3 600 h，年总辐射量可达7 000～8 000 MJ/m2，为 全 国 第 二 高 值 区[3]。但 高 海拔地区空气稀薄，地面接收辐射多、保温性差，导致当地环境温度波动幅度大。对于由众多光伏组件组成的大型光伏电站，所处环境温度的波动易导致光伏阵列出现温度失衡，直接影响电站的运行，在一定程度上对电网的稳定性也会产生不利的 影 响[4]，[5]。

为提高电站的运维水平，学者们已就温度对光伏组件性能的影响做了大量研究。Qais Mohammed Aish研究发现，单晶硅、多晶硅与硒化铜铟镓分别在25℃，35℃和45℃时，电量下降程度 依 次 为0.54%/℃，0.49%/℃和0.38%/℃[6]。Emad Talib Hahsim依据巴格达市的气候条件，研究了温度对单晶硅、多晶硅、非晶硅与铜锢镓硒几种太阳能电池性能参数的影响，结果表明：单晶硅、多晶硅、非晶硅与铜锢镓硒短路电流的增幅分别为0.3 mA/℃，4.4 mA/℃与0.9 mA/℃；非 晶 硅 最 适于高温运行，但转换效率最低[7]。Dubey S提出光伏组件的光电效率、输出功率与工作温度呈线性关系，对温度敏感度较低的光伏组件更适合高温环境作业，而对温度响应更强的光伏模块则应作业于低温环境[8]。王琪和王露均基于Matlab工具进行了光伏发电系统的构建，前者确定了光伏发电系统在环境温度为50℃时的输出特性优于25℃；后者提出当光伏组件工作温度与环境温度相差超过75℃时，光伏组件的光电转换效率开始下降[9]，[10]。张雪莉依托某100 kW光伏电站的历史运行数据，基于统计学方法，对环境温度大于10℃的光伏组件输出特性进行了定性、定量分析，得出日均温度越高，发电功率越多的结论[11]。

以上学者对不同环境温度下的光伏组件特性进行了分析，但目前关于高海拔地区交变温度对光伏组件性能影响的研究较少。本文通过分析电站环境温度特点及光伏组件与外界的换热方式，利用Solidworks建立光伏组件的几何模型，并根据换热方式加载模型热源与边界，考虑光伏组件与外界的动态换热，采用Ansys Workbench中的瞬态热分析环境温度对光伏组件输出特性的影响[12]。

1 光伏组件运行环境

1.1 环境温度特征

海西地处青藏高原北部、青海省西部，平均海拔3 000 m，为典型高原大陆性气候；四季不分明，太阳辐射强，昼夜温差大，常年干旱、多风、少雨，年均气温为5.5℃[13]。文中以每季度典型月（1月-春、4月-夏、7月-秋、10月-冬）的 第15日 全 天 为时间点，进行电站周围环境温度的气象数据监测。24 h内的气温随时间变化曲线如图1所示。

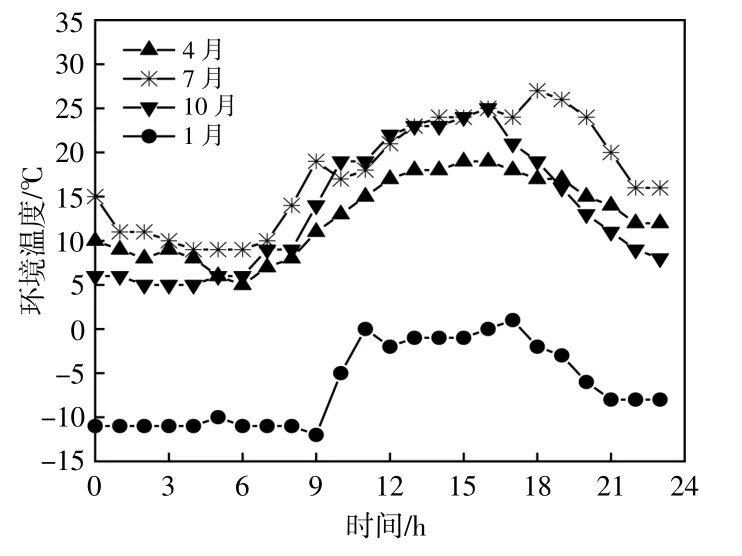
图1 环境温度随时间变化曲线Fig.1 Ambient temperature curve with time

由 图1可 知：11：00-18：00温 度 普 遍 较 高，而夜间温度低，日间最高温和夜间最低温相差15～20℃；从季节分布上，夏季气温最高，春秋季次之，冬季气温最低，多为0℃或以下。设置[-15℃，30℃]为本文交变温度的区间，温度梯度为15℃。此外，由图1还可以看出，8：00-12：00的温度增幅最明显。因此，文中模拟温度突变和温度渐变两种作业环境。突变环境下，环境温度依次设置为-15℃，0℃，15℃，30℃，间 隔1 h；渐 变 环 境 的 间隔时间也为1 h，不同的是温度渐变中，光伏组件经历-15℃温度1 h后，需置于标准参考温度25℃中1 h，再置于0℃环境中，依次进行。

1.2 热模型

基于硅材料的光伏组件在与外界环境进行热量交换时，其截面的能量分布如图2所示[14]。

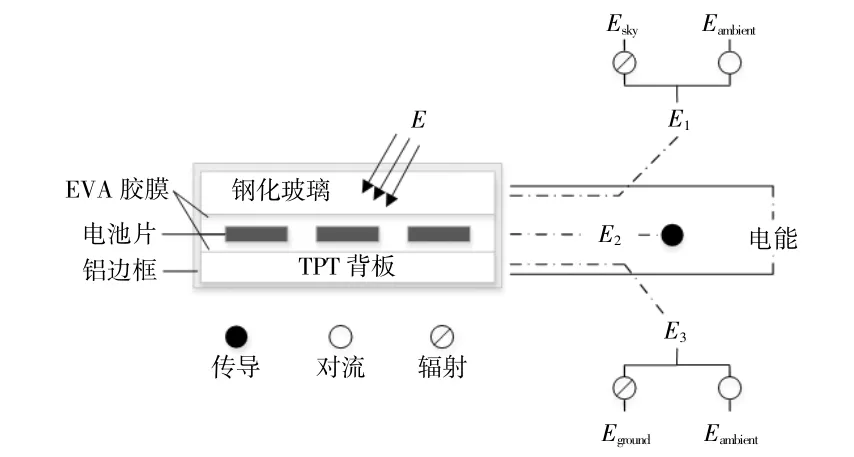
图2 光伏面板截面的能量分布Fig.2 Distribution of energy in longitudinal-section of photovoltaic panel

由图2可知，光伏组件与外界环境的换热方式为几种传热方式的耦合作用，主要包括传导、对流和辐射。图中：E为光伏组件面板接收的太阳辐射总量；E1，E3分别为钢化玻璃、TPT背板层向外损耗的能量，包括辐射和对流两种能量损耗；E2为光伏组件内部的热量生成。辐射热损包括钢化玻璃层向天空、背板层向地面两种辐射模式，即图中的Esky，Eground。对流损耗则发生在周围大气之间，分为强制与自然两种对流方式。因此文中根据光伏组件的换热模式，基于下列假设进行Ansys Workbench热分析：

忽略组件层间反射及铝边框四周的热交换，前者反射率较小，后者纵向截面积较小；光伏组件水平放置；辐照度取标准作业环境下的太阳辐射，即环境温度为25℃，AM1.5太阳光谱辐照度分布时的1 000 W/m2太阳辐照度；辐射换热中，视天空和地面温度为环境温度；对流换热时，不考虑风速的影响；组件对交变温度场响应为瞬时响应，材料性能参数为各向同性，与温度无关。

2 建模与仿真

2.1 几何模型

文中利用Solidworks软件建立多晶硅光伏组件的几何模型 （图3），Solidworks具备与Ansys Workbench软件接口特性，建立的几何模型数据可通过接口直接传输至Workbench中进行仿真分析。一般现场作业的光伏组件尺寸多为1 650 mm×995 mm×40 mm，层压件结构四周通过密封胶与铝合金边框粘连固定得到。其中，层压结构主要包括钢化玻璃、EVA（醋酸乙烯乙酯）胶膜、光伏电池层和TPT背板膜（聚氟乙烯复合膜）几部分，光伏电池层嵌于两层EVA胶膜之间，具体结构如图2所示。考虑实际作业的组件尺寸太大，且光伏电池层由多个单体光伏电池组成，结构较为复杂，而单体电池表面布有金属栅线，通过互链条一正一负串联焊接硅片而成。若按照1∶1建模，在进行仿真时，不易进行网格划分，同时会增加求解时间。因此，对光伏组件按照1∶3建模，同时简化金属栅线、互链条及背板接线盒部分。

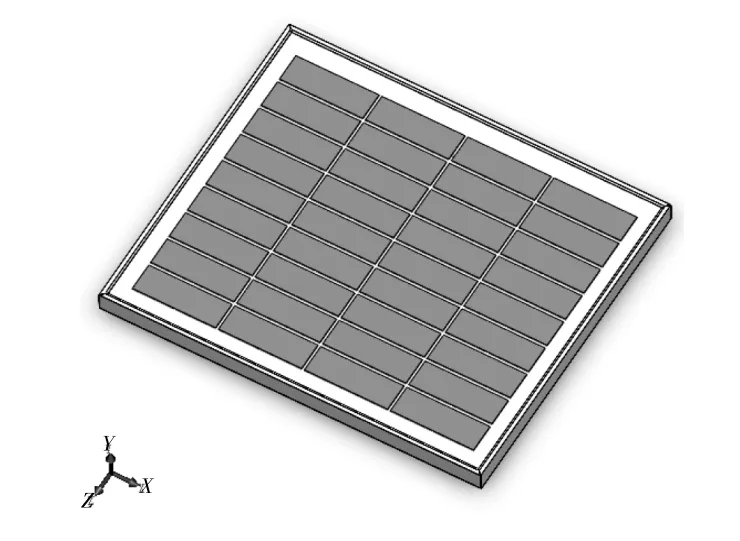
图3 几何模型Fig.3 Geometric model

光伏组件各组成结构的性能参数如表1所示[15]。

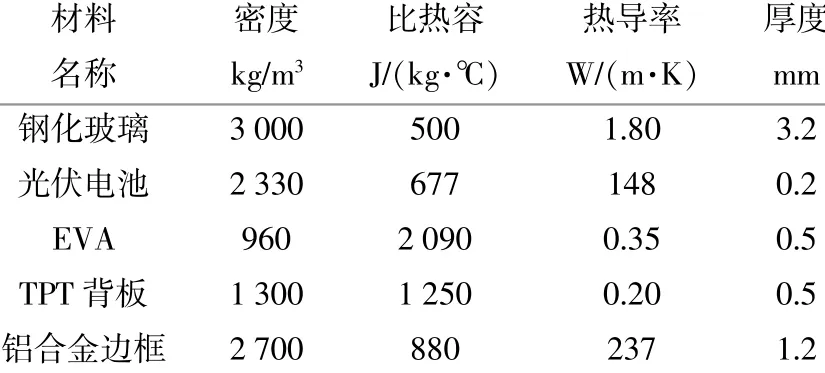
表1 组件性能参数Table 1 Performance parameters of photovoltaic module

2.2 设置热载与边界条件

假定模型作业时天气晴朗、无风，1 000 W/m2的太阳辐照度作为模型唯一热源。模型初始温度为25℃，根据上文提出的假设，模型的边界条件作如下设置：

①模型上下表面设置为辐射边界，玻璃层、背板和铝边框辐射率分别取0.85，0.9和0.71[16]；

②模型表面添加对流边界，对流传热系数h的取值根据Nolay方程进行计算[14]：

式中：v为风速值，因不考虑风速影响，与外界只通过自然对流的方式实现热量交换，故v取0。

组件背板的冷却效果多认为低于上表面，其对流传热系数大小也多取表面值的一半。因此，文中模型表面与背板的对流传热系数取值分别为5.82 W/（m2.℃），2.91 W/（m2.℃）。

3 结果与分析

3.1 光伏组件温度场分析

对光伏组件模型选取温度探测点，以记录模型在温度突变和温度渐变两种环境下各部分温度随时间的变化情况。光伏电池因由多个单体电池组成，将边缘的4个顶点作为温度测量点，其余部分各一个，得到模型温度随时间的变化曲线，如图4所示。

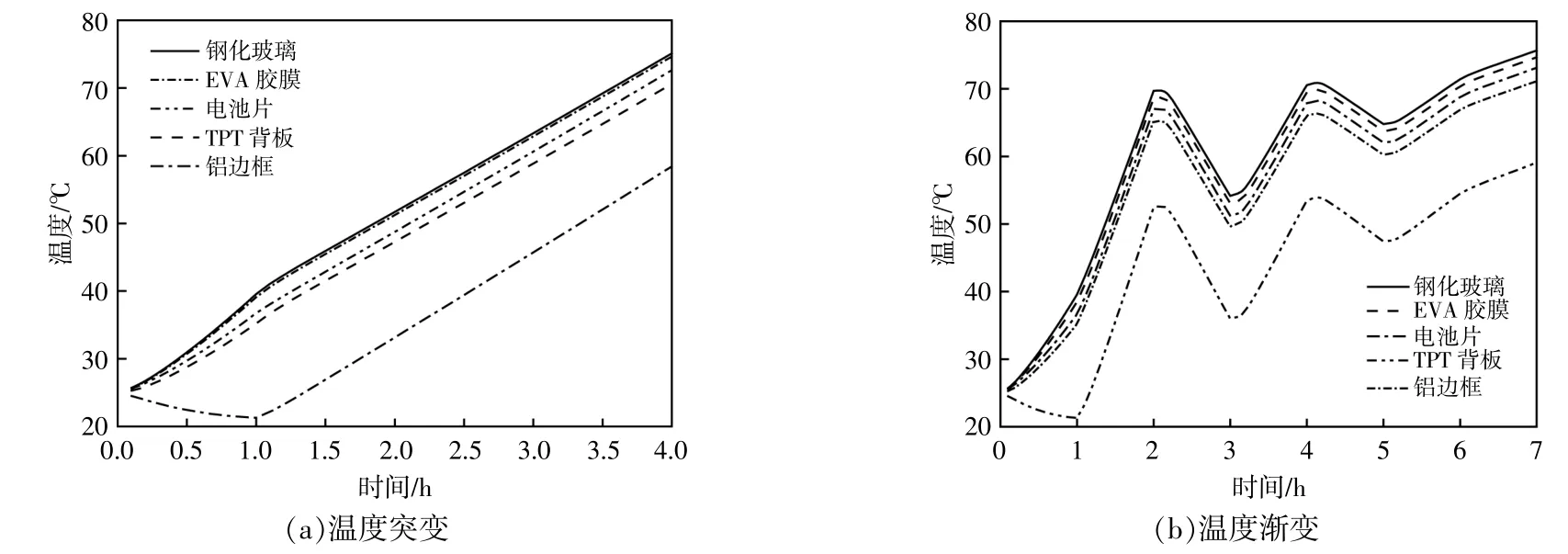
图4 不同条件下组件模型温度变化曲线Fig.4 Temperature curve of component model under different conditions

由图4可知：当外界环境温度突变时，光伏组件各部分温度线性上升；当处于渐变环境温度时，温度起伏式上升。但模型热量均自上而下传递，两种环境下的最高温度和最低温度均发生在表层钢化玻璃和铝合金边框位置处，模型温度分布不均匀。由表1可知，钢化玻璃的热导率较低，导热性差，且厚度远大于其他层材料，温度降低较慢，所以温度最高。在实际中，钢化玻璃的耐高温性能良好，是普通玻璃的3倍，同时可承受250℃以上的温差变化。而铝边框处温度最低，其热导率数值较其他部位大，传热速度较其他部位也更快。因此，该模型从边框到中心存在温度梯度。对比图4（a），（b）温 度 变 化 曲 线 可 知，EVA胶 膜 层 的 温 度仅次于钢化玻璃，而EVA胶膜层厚度和热导率相对较小，热量容易在该层积聚，不易扩散。一旦温度过高，EVA胶膜可能会丧失粘结作用，使得光伏组件的层压件各层间相互剥离，直接引起光伏组件失效。

3.2 交变温度下光伏组件电气输出特性

图5为30℃时两种温度环境下的光伏电池层温度云图分布示意图。

图5 电池层温度分布Fig.5 Temperature distribution of cells layer

由图5可知：两种环境温度变化下的光伏电池热量从中心向边缘扩散，呈梯度分布；与模型温度变化一致，温度场分布不均匀，原因是不同位置处的单体电池温度不相等；单体电池最大温度与最小温度差为2℃，温度梯度较小。这种温度分布的不平衡影响会随光伏组件串、并联数目的增多而加剧，大型光伏发电系统由很多单一光伏组件串、并联构成，光伏阵列不同位置的光伏组件温度不一致，直接导致光伏系统的不稳定输出。考虑文中建立的模型尺寸较小，视该光伏电池只有一个温度，取不同温度下的光伏电池的平均温度值，如图6（a）所 示；利 用 式（1）[14]计 算 组 件 不 同 环 境 温 度变化下的光电转换效率η，如图6（b）所示。

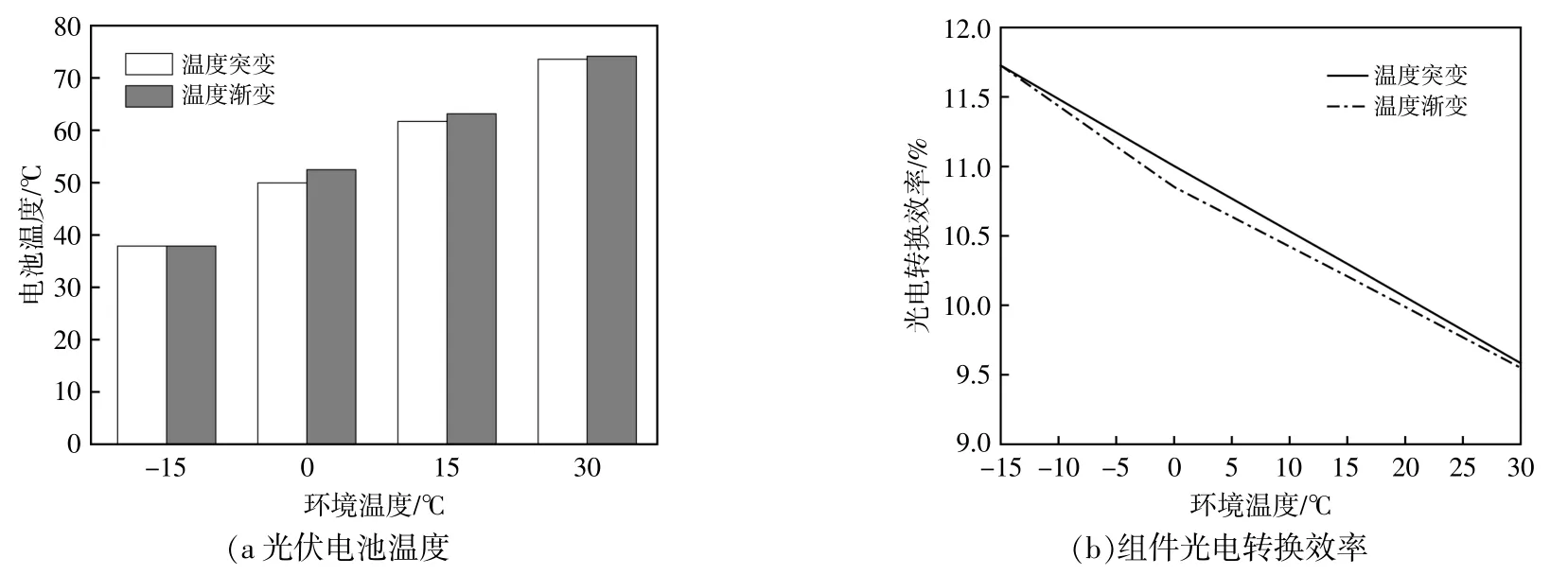
图6 不同环境温度条件下的光伏组件电气特性Fig.6 Electrical characteristics of photovoltaic modules under different ambient temperature conditions

式中：ηref为组件的参考光电转换效率；β为光伏组件的晶硅温度系数，β取值为0.004 8℃-1[17]；Tcell为电池温度，与环境条件有关；Tref为参考温度，取值为25℃；γ为组件的辐照度系数，一般情况下γ视 作0 W/（m·K）；φsolar为 辐 照 度，取 值 为1 000 W/m2。

由图6可知：两种温度环境下的光伏电池温度变化与环境温度的变化趋势一致，即电池温度随环境温度的升高而升高；光电转换效率随环境温度的升高而下降；当环境温度相同时，温度渐变下的光伏电池的光电转换效率低于温度突变。这表明，环境温度波动程度越大，即温差越大，光伏组件性能输出越不稳定。

3.3 仿真结果验证

文献[2]基于IEC61853-1标准提供的测试矩阵，以瞬态太阳光模拟器为光源，对经预处理检测性能稳定的单一光伏组件进行测试，得到了不同辐照度、不同环境温度下的光伏组件的最大输出功率。结合本文模型输入的太阳辐照度大小，对其输出功率曲线进行数据提取，利用插值法获得辐照度为1 000 W/m2时，25～75℃的光伏组件输出功率，如图7所示。

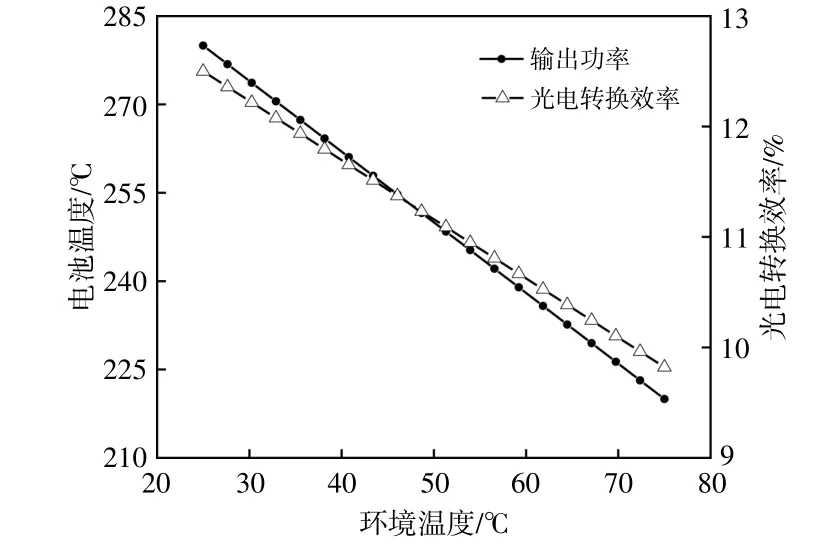
图7 各参数随环境温度的变化情况Fig.7 Variation of various parametres with ambient temperature

由图7可知：输出功率与环境温度呈负相关，即输出功率随环境温度的升高而线性降低；光电转换效率的整体变化趋势也是随着温度的升高而下降，与本文仿真模拟得到的光电转换效率随温度的变化曲线趋势相符。

4 结论

①环境温度突变和渐变两种条件下的光伏组件温度不均匀，最高温和最低温分别发生于表层钢化玻璃和边框处。不同位置的单体光伏电池热量差异，造成整个光伏电池层的温度呈梯度分布。这种温度分布不平衡会随光伏组件串、并联数目的增多被放大；光伏阵列的温度失衡，直接导致光伏发电系统的不稳定输出，会增加电网的调配难度。

②仿真结果表明：恒定的太阳辐照度下，光伏电池温度与环境温度为正相关且线性增加；光电转换效率为温度的负函数，随着环境温度的增加而下降。