分布参数系统的模糊插值推理建模
杨文光,韩元良,王 清,高艳辉
(华北科技学院 理学院,河北 三河 065201)
在现实世界中,分布参数系统是一类广泛存在的具有无穷维与时空分布特性的系统.如化学反应中物质的分布、超导体的导电、弹性梁的变形运动、污染物在区域内的扩散等都属于典型的分布参数系统实例.对于分布参数系统,不同于集中参数系统,一般采用机理建模法得到偏微分方程.若不能搞清楚分布参数系统的内部运行机理,就很难构建出偏微分方程模型.如何有效使用各种传感器获取的系统时空数据,构建反映系统内部信息的黑箱模型成为问题研究的突破口.Takagi等提出了T-S型模糊系统,成为与Mamdani型模糊系统一样深受研究者重视的两大模糊系统之一.李洪兴等率先提出了模糊推理建模法,成为继机理建模法和系统辨识建模法之后的第三种建模方法,该方法可以利用采样数据,依据插值机理建立对应系统的变系数非线性微分方程(组)——HX方程.模糊推理建模法作为处理非线性系统建模的新方法,仅需利用有限采样数据就能较为便捷地得到所研究问题的逼近模型,为问题解决提供了崭新思路.为了方便进行系统的定性或定量分析,边缘线性化方法对模糊推理建模法进行了改进,可以建立变系数线性模型.随着时间的推移,模糊推理建模方法不断发展,基于Fuzzy推理的时变系统建模可以应用于时变系统的建模上,拓展了模糊推理建模法的应用范围.模糊推理建模在理论研究推进的同时,也被用于混沌系统和单水箱液位系统的建模,说明该方法具有较好的实际应用价值.基于模糊变换的新的模糊推理建模法,对模糊推理建模法进行了有意义的推广.张春岭首次将T-S型模糊系统引入到HX方法中,尝试解决了集中参数系统中时变与时不变情况下的建模问题.张保杰等在模糊推理建模时使用矩形隶属函数实现了线性化,获得了更高的建模精度.以上文献都将研究重心放在了集中参数系统上,模糊推理建模法同样可以被应用于解决分布参数系统的推理建模,且建模精度有更大的改进空间.
论文将在上述文献工作基础上,将T-S型模糊系统与模糊插值机理结合设计出T-S型模糊分片Lagrange插值推理建模法.理论推导证明论文所提出的分片T-S型模糊插值推理建模满足插值性,仿真实验验证了理论的有效性,使得HX方程成为分布参数系统的有效表示模型,促使时空复杂度得到极大简化,丰富了模糊推理建模方法.
1 T-S型模糊推理建模
定义1
设X
=[a
,b
],T
=[a
,b
]分别为x
,t
的论域;A
={A
}(1≤≤),B
={B
}(1≤≤)分别为相应论域上的模糊划分,x
,y
分别为模糊集A
,B
的峰点,满足条件a
=x
<x
<…<x
=b
;a
=t
<t
<…<t
=b
.视A
,B
为语言变量,可形成如下的T-S型模糊规则库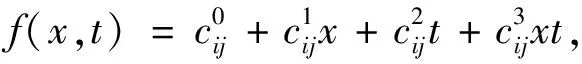
(1)
定义2
设A
的隶属函数为“三角波”
(2)
设B
的隶属函数为“三角波”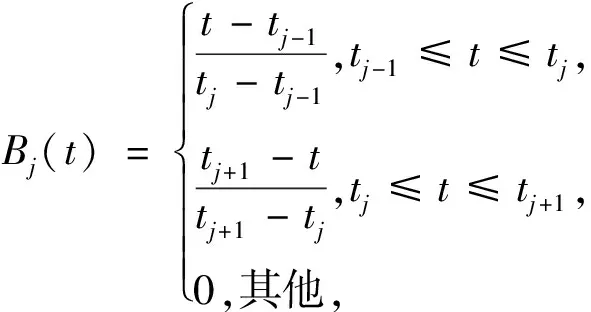
(3)
其中:i
=1,2,…,p
-1;j
=1,2,…,q
-1.且约定x
=x
,t
=t
.当i
=p
,j
=q
时,有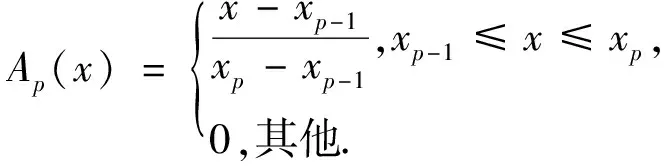
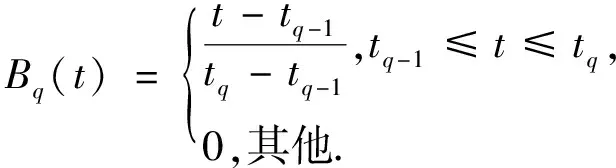
(4)
图1给出了A
的“三角波”隶属函数示意图,B
具有相似的“三角波”隶属函数.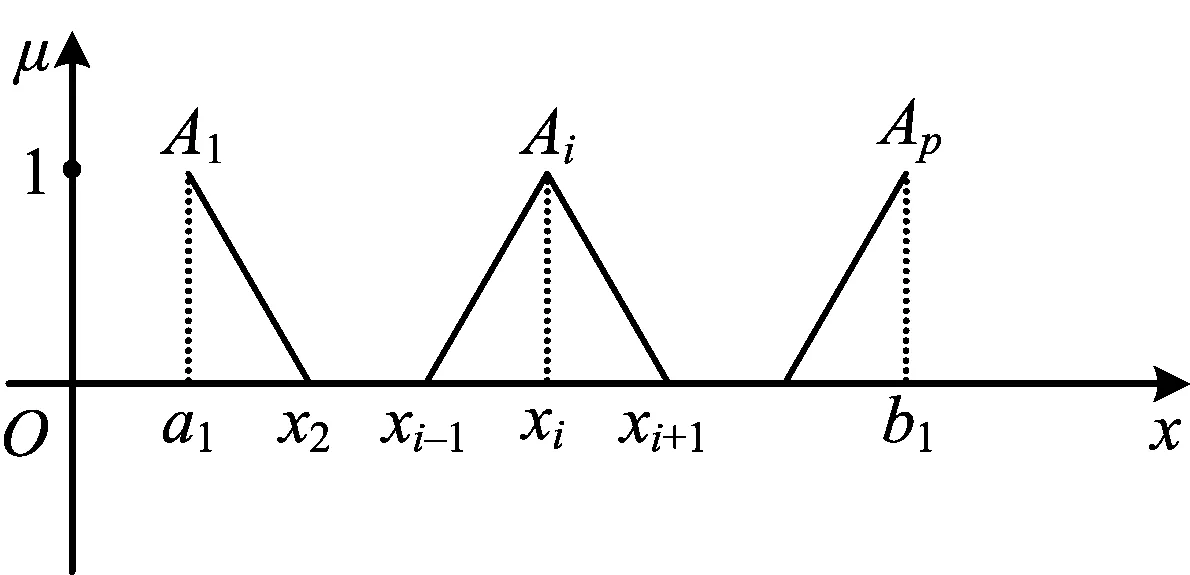
图1 Ai的“三角波”隶属函数
基于规则库(1)的T-S型模糊系统f
(x
,t
),在选择单点模糊化、乘积推理机和中心解模糊化的情况下可表示为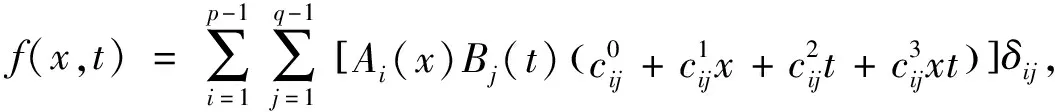
(5)
其中:δ
为分片激活函数,表达式为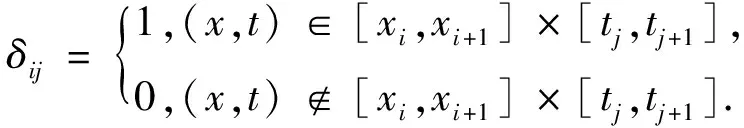
定理1
当(x
,t
)∈[a
,b
]×[a
,b
]时,在上述假定和公式(2)~(5)作用下,基于(1)式的二元分布参数系统u
(x
,t
)的输入输出近似模型f
(x
,t
)可简化表示为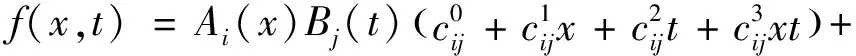
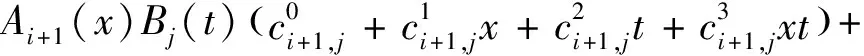
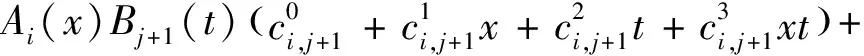
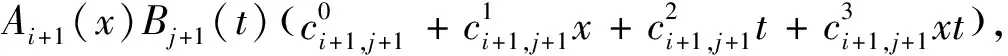
(6)
其中
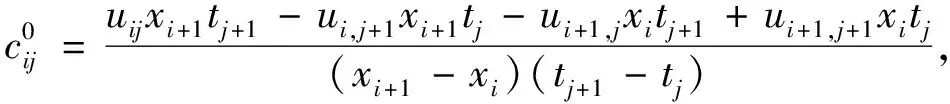
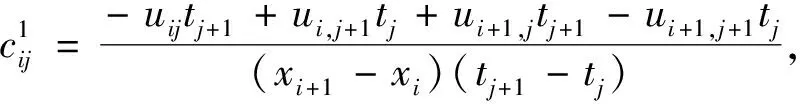
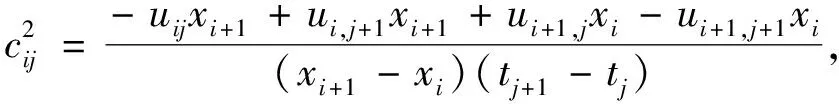
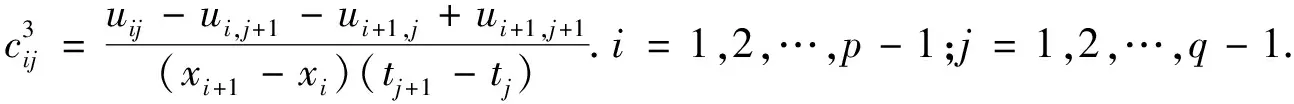
证明
将输入输出论域划分为(p
-1)×(q
-1)片,提取出p
×q
组数据节点(x
,t
,u
),形成如(1)式的模糊规则库.由于模糊集A
与B
均为三角波隶属函数(m
=1,2,…,p
;n
=1,2,…,q
),故∀(x
,t
)∈[a
,b
]×[a
,b
],存在相应的i
,j
,使得x
∈[x
,x
+1],t
∈[t
,t
+1],有0≤A
(x
)≤1,0≤A
+1(x
)≤1,A
(x
)+A
+1(x
)=1,0≤B
(t
)≤1,0≤B
+1(t
)≤1,B
(t
)+B
+1(t
)=1,且A
(x
)=0,m
≠i
,i
+1;B
(t
)=0,n
≠j
,j
+1.所以,对于任意输入(x
,t
),p
×q
条规则中有且仅有4条规则同时被激活,(5)式可简化表示为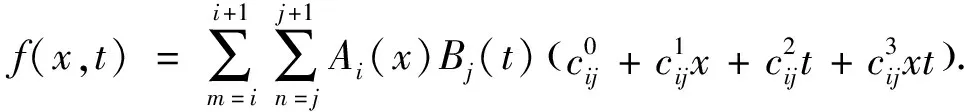
(7)
又因为二元分布参数系统u
(x
,t
)满足Lipschitz条件,所以u
(x
,t
)在[a
,b
]×[a
,b
]上一致连续,也就满足连续可微的条件.考虑以点(x
,t
),(x
,t
+1),(x
+1,t
),(x
+1,t
+1)作为顶点的矩形邻域,对u
(x
,t
)进行分片线性Lagrange插值,得到f
(x
,t
)≈u
(x
,t
)=l
u
+l
+1,u
+1,+l
,+1u
,+1+l
+1,+1u
+1,+1,(8)
其中:f
(x
,t
)是u
(x
,t
)的T-S模糊模型,且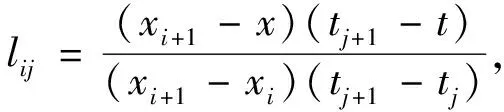
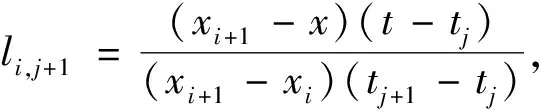
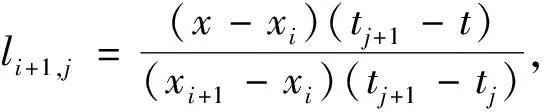
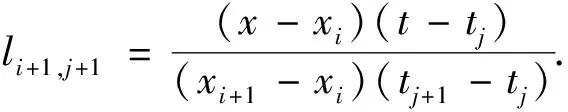
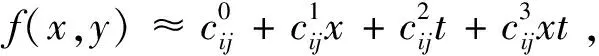
定理2
依据公式(5)设计的T-S型模糊插值推理模型满足插值性.证明
由定理1可知,对于任意输入(x
,t
)∈[a
,b
]×[a
,b
],存在对应的矩形邻域[x
,x
+1]×[t
,t
+1],使得(x
,t
)∈[x
,x
+1]×[t
,t
+1].i
=1,2,…,p
-1;j
=1,2,…,q
-1.当(x
,t
)分别与节点(x
,t
),(x
+1,t
),(x
,t
+1),(x
+1,t
+1)重合时,对插值性加以验证.将(x
,t
)=(x
,t
)代入公式(6),得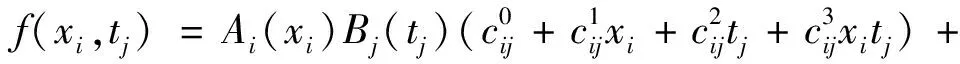
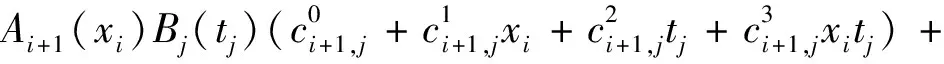
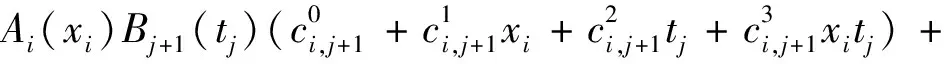
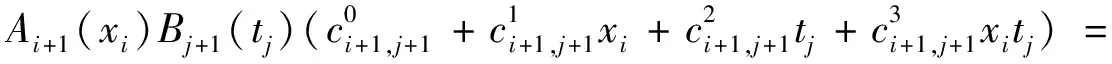
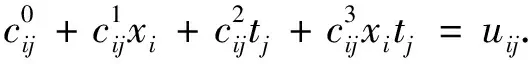
f
(x
,t
)在其他节点上同样满足插值性.证毕.2 T-S型模糊插值推理建模算法实现
T-S型模糊插值推理建模在有限采样数据基础上,充分利用数据内在的插值逼近特性,反映了采样数据的关键支撑作用.现选择一种抛物型偏微分方程为例,表述分布参数系统的T-S型模糊插值推理建模的实现过程.
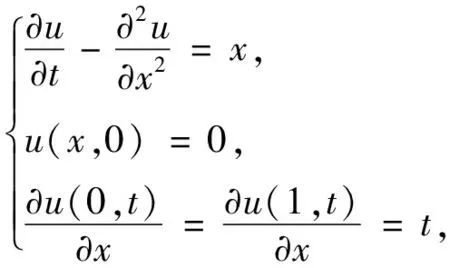
(9)
T
=1,该偏微分方程的精确解为
(10)
通过时空传感器获得模型的真实系统的p
×q
组时空输入输出数据(x
,t
,u
).假设对x
,t
已完成序的排列(m
=1,2,…,p
;n
=1,2,…,q
),其中(x
,t
,u
)恰好落在需要建模区域[0,1]×[0,1]内(i
=1,2,…,p
;j
=1,2,…,q
),这些p
×q
组数据可以形成规则(1)形式.在论文仿真中公式(10)充当了时空传感器角色,具体建模步骤如下:步骤1 以公式(10)作为真实系统,确定x
与t
的取值范围,然后确定论域X
=[a
,b
],T
=[a
,b
],其中a
=min(x
),b
=max(x
),a
=min(t
),b
=max(t
),max(),min()分别为MATLAB软件中的取大、取小操作.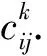
x
,t
)代入真实系统(10),得到真实系统u
(x
,t
),完成与步骤3所得逼近模型f
(x
,t
)的各项性能比较.采用MATLAB7.5.0(R2007b)按照上述步骤完成近似模型建模.在论文建模中选择p
=5,q
=5,仅有规则25条,M
=101,N
=101.图2给出了采样数据输出曲面,所包含的系统信息还比较有限.图3是真实系统输出曲面,图4是T-S模糊推理建模逼近输出曲面,二者基本上无差别.图5给出了逼近模型与真实系统之间的建模误差,最大误差为2.220 4×10,误差总和仅为1.106 3×10.采用论文建模方法程序运行总时长仅为0.722 36 s.综上可知,论文建模方法对于解决分布参数系统建模的逼近精度较高,运行时间较短.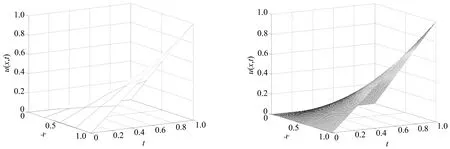
图2 采样数据输出曲面 图3 真实系统输出曲面
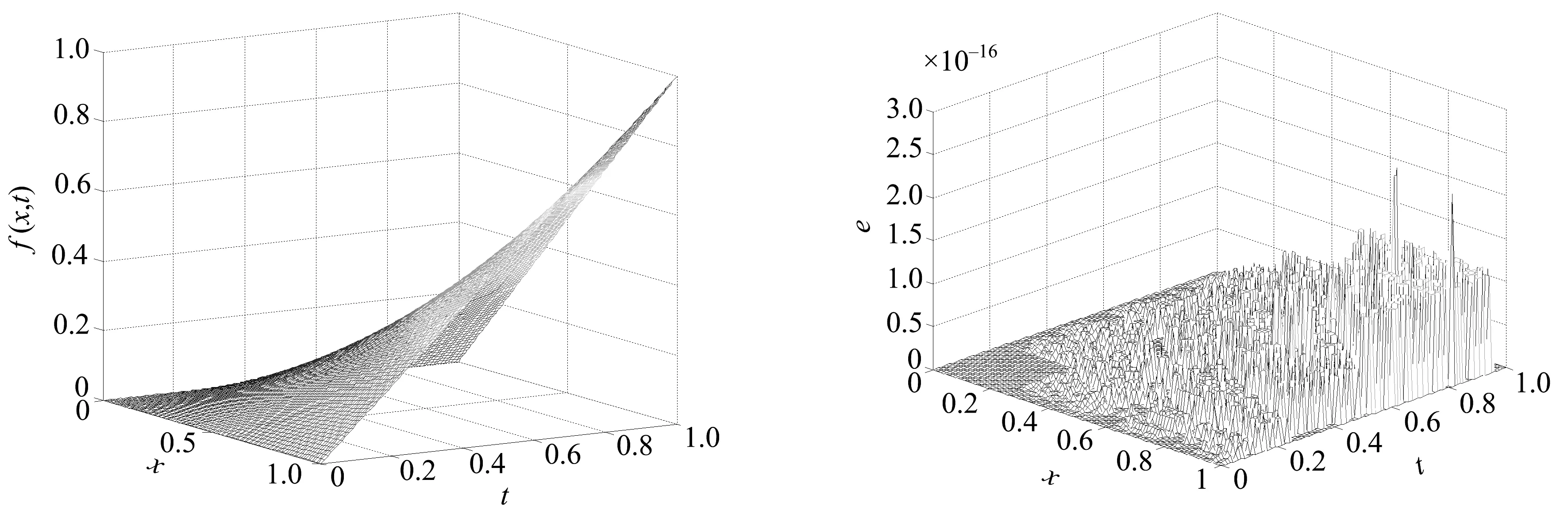
图4 模糊插值推理建模逼近输出曲面 图5 误差曲面
3 结束语
论文通过T-S模糊系统与HX方法的结合,设计出了关于分布参数系统的T-S型模糊插值推理建模法.在T-S模糊系统的具体参数设置上利用了多元函数的Lagrange插值,保证在理论上具有较高逼近精度.T-S型模糊插值推理建模法可以有效利用有限采样数据信息,反映了分布参数系统时空变化规律.T-S型模糊插值推理建模法符合插值机理,表示简单,参数易求.结合算法实例验证了方法的可行性,建模精度较高,运行时间较短.该推理建模方法极大丰富了HX模糊推理建模法,是一种有效的推广与应用.

