风速波动时基于UKF-DFNN的变桨距控制

王江江，王维庆*，王海云，萨妮耶·麦合木提

(1.新疆大学 电气工程学院，新疆 乌鲁木齐 830047；2.新疆大学 可再生能源发电与并网技术教育部工程研究中心，新疆 乌鲁木齐 830047)

随着风电装机容量的增加，变桨距风电机组受到广泛关注.风速大于额定风速时，风电机组可以通过控制桨距角，使输出功率回归于额定功率，保障风机运行安全.变桨距控制系统的非线性，会导致运行参数不稳定及精确数学模型难以得到等情况出现.

对于风电机组变桨距控制参数的不稳定，文献[6]提出了双模糊比例积分微分(proportion integral derivative，简称PID)变桨距控制策略，大于额定风速时双模糊PID控制器对桨距角进行调整，提高了输出功率的稳定性，但整定过程较长.在PID控制的基础上，文献[7]提出一种抗积分饱和的PID调节方式，根据风速判断是否退出积分器，提高了系统快速响应能力、输出功率稳定性.对于风速快速波动带来的问题，文献[8]提出了一种变速恒频自抗扰控制方案，该方案桨距角的调节速度更快，提高了抗干扰能力.文献[9]提出了BP-PID整定的控制策略，与常规PID控制相比，该策略的风电机组输出功率和转速的超调量较小，调节时间明显减少.文献[10]提出了将模糊免疫PID用于变桨距控制，降低了转子转速的波动，减小了系统的超调量.文献[11]提出了一种基于RBF神经网络的变桨距滑模控制方案，减轻了桨距角的抖振，提高了系统的稳定性和鲁棒性.上述研究主要侧重于桨距角的响应速度及输出功率的稳定性，没有对有扰动的变桨距系统进行研究.鉴于此，笔者针对风电机组扰动信号引起的功率波动及变桨距系统频繁启停的问题，提出一种基于无迹卡尔曼滤波(unscented Kalman filter,简称UKF)与动态模糊神经网络(dynamic fuzzy neural network,简称DFNN)相结合的变桨距控制策略.该策略利用UKF对风电机组转速与输出功率进行滤波，采用DFNN动态调整参数权重，实现变桨距控制.该策略提高了桨距角指令值的精确度，减小了桨距角的波动，有助于输出功率的稳定，增强了风速波动时系统的鲁棒性.

1 风电机组的数学模型

由空气动力学可知，风电机组从风能捕获的最大机械功率为

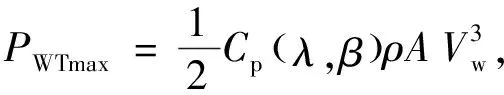
(1)

其中：

C

(

λ

,

β

)为风能利用系数，

λ

为风轮叶尖速比，

β

为桨距角，

ρ

为空气密度，

A

为风轮叶片扫过的面积，

V

为上风向风速.

最佳转速对应的角速度为

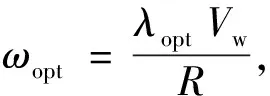
(2)

其中：

λ

为捕获最大机械功率时的最优风轮叶尖速比,

R

为风轮半径.

最佳风能利用系数为

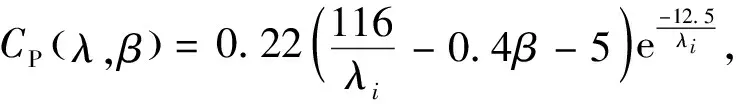
(3)

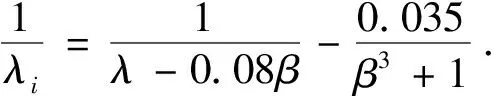
2 风电机组变桨距原理

在风电机组数学模型的基础上，利用 Matlab得到风电机组变桨距的叶尖速比与风能利用系数的关系曲线如图1所示.

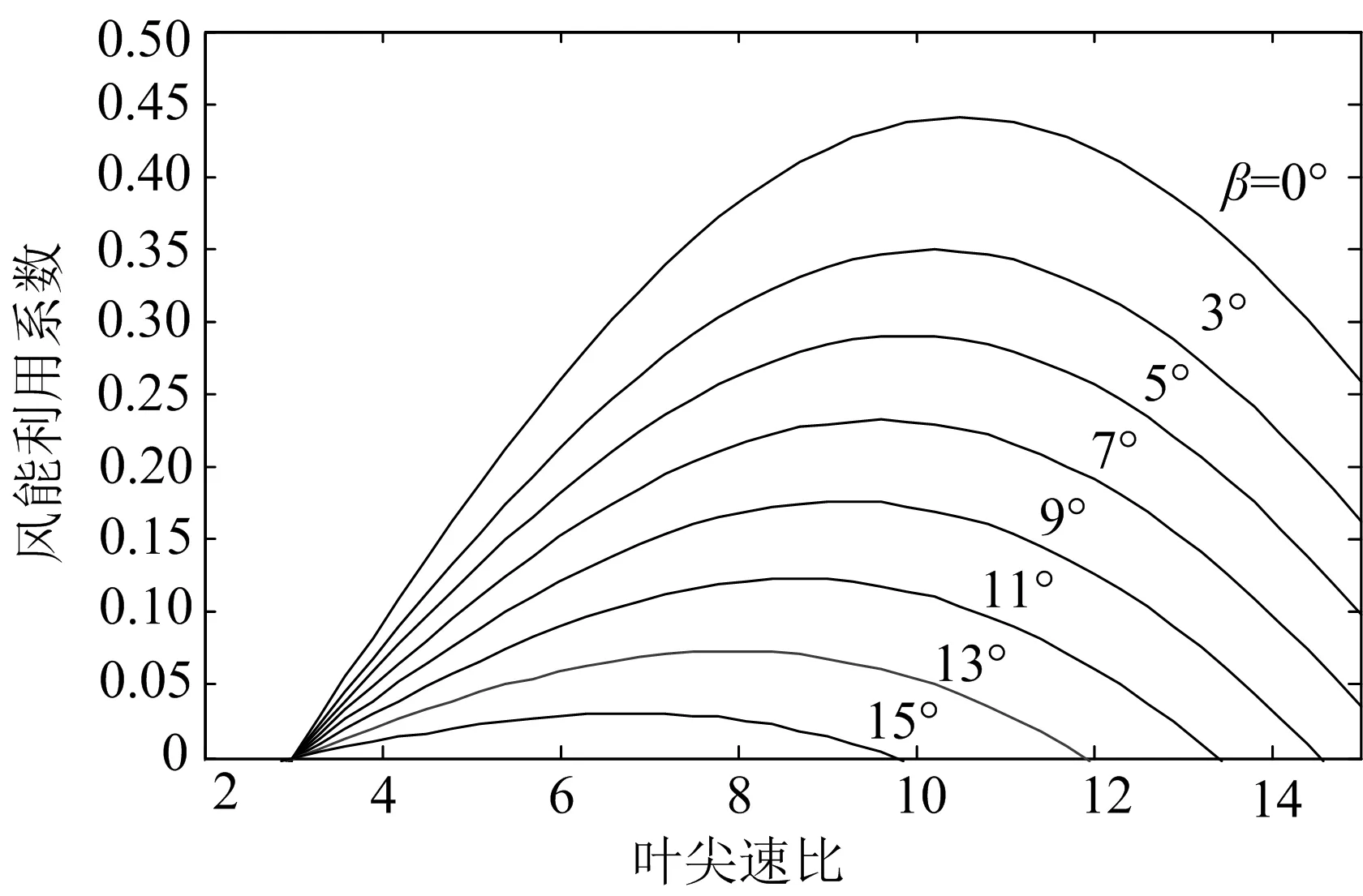
图1 风电机组变桨距的叶尖速比与风能利用系数的关系曲线

通过调整桨叶节距、改变气流对叶片的攻角，实现变桨距控制.从图1可知:对任意固定不变的叶尖速比

λ

，桨距角减小时风能利用系数

C

增大；对任意固定不变的桨距角

β

，叶尖速比

λ

增大时风能利用系数

C

先增大后减小，故存在最大的风能利用系数

C

.当风速小于额定风速时，风电机组通过改变发电机转子转速，使风能利用系数

C

最大，此时桨距角接近0°；当风速大于额定风速时，变桨距系统通过调整桨距角，改变风电机组的空气动力转矩，进而改变发电机的输出功率，使输出功率保持恒定.

3 UKF-DFNN控制策略分析

3.1 UKF工作原理

为了提高变桨距控制系统的性能，针对系统的非线性以及控制信号中存在随机干扰等问题，利用UKF来提高变桨距控制系统的抗干扰能力，优化变桨距系统的动、静态性能.由于UKF具有较高的滤波精度，对于非线性的风力发电系统无须线性处理，也不需计算复杂的雅克比矩阵，就可提高卡尔曼滤波的运算速度；对变桨距控制系统中随机产生的干扰信号能较好过滤，使有效信号正常输出.UKF的计算过程是一个不断“预测-修正”的过程，通过计算可得到精确均值和协方差.在系统运行过程中，实时测量数据并计算新的滤波值，能减小差值波动，提高输出功率的精确度.

3.2 UKF的步骤

第1步 从反馈的转子转速及功率中各选取2

n

+1个数据(

n

为状态维数).网络输入向量及输出期望值表达式分别为(

k

+1)=

f

{[(

k

),(

k

)],(

k

)}，

(4)

(

k

)=

h

((

k

),(

k

))，

(5)

其中：(

k

)为网络输入向量,(

k

)为已知的

n

维输入向量，(

k

)为过程噪声向量，(

k

)为测得的噪声向量，(

k

)为网络输出期望值.可利用式(4)，(5)分别计算网络输入向量及输出期望值.

第2步 根据下式计算采集点的转子转速及功率

(

k

+1|

k

)=

f

[

k

,(

k

|

k

)]，

i

=1,2,…,2

n

+1.

(6)

第3步 系统状态量的一步预测值及协方差矩阵的计算公式分别为

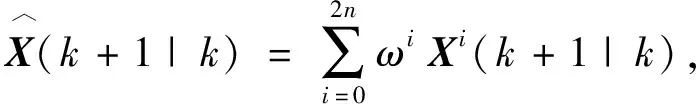
(7)

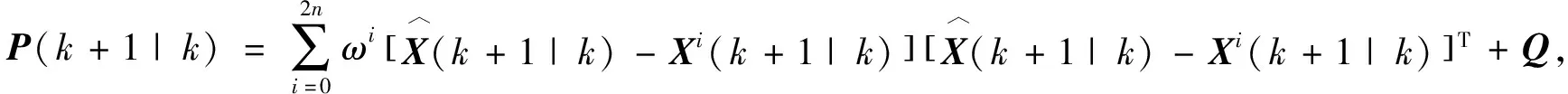
(8)

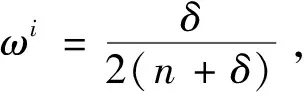
第4步 将式(7)，(8)代入下式，得到新的Sigma点集

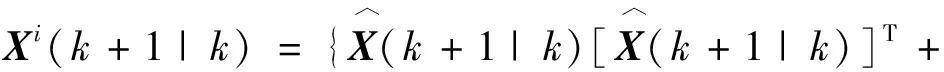
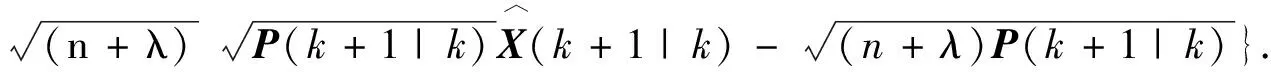
(9)

第5步 利用UT变换生成的点集，计算输出功率及转子转速的预测值及方差.预测值及方差的计算公式分别为

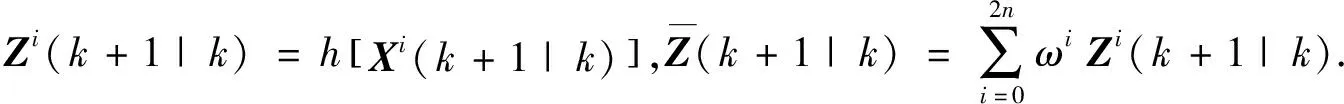
(10)

第6步 卡尔曼增益矩阵的计算公式为

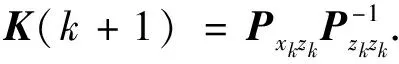
(11)

利用式(11)计算卡尔曼增益矩阵.

第7步 分别利用

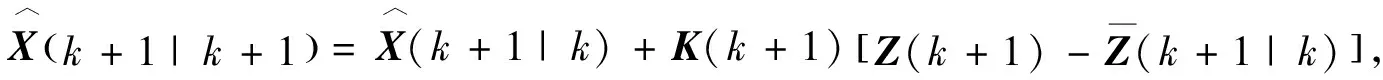
(12)

(

k

+1|

k

+1)=(

k

+1|

k

)-(

k

+1)(

k

+1)，

(13)

更新系统的状态、协方差.通过不断更新状态及协方差，修正输出功率，提高预测精度.

3.3 DFNN控制器的工作原理

DFNN控制器对UKF输出的风电机组功率和转速进行实时处理、在线辨识，制定优化的模糊规则，输出理想的桨距角指令值，提高风能利用系数.采用DFNN变桨距控制，能减小风电机组反馈数据的波动范围,提高系统的稳定性.DFNN控制器结构如图2所示.

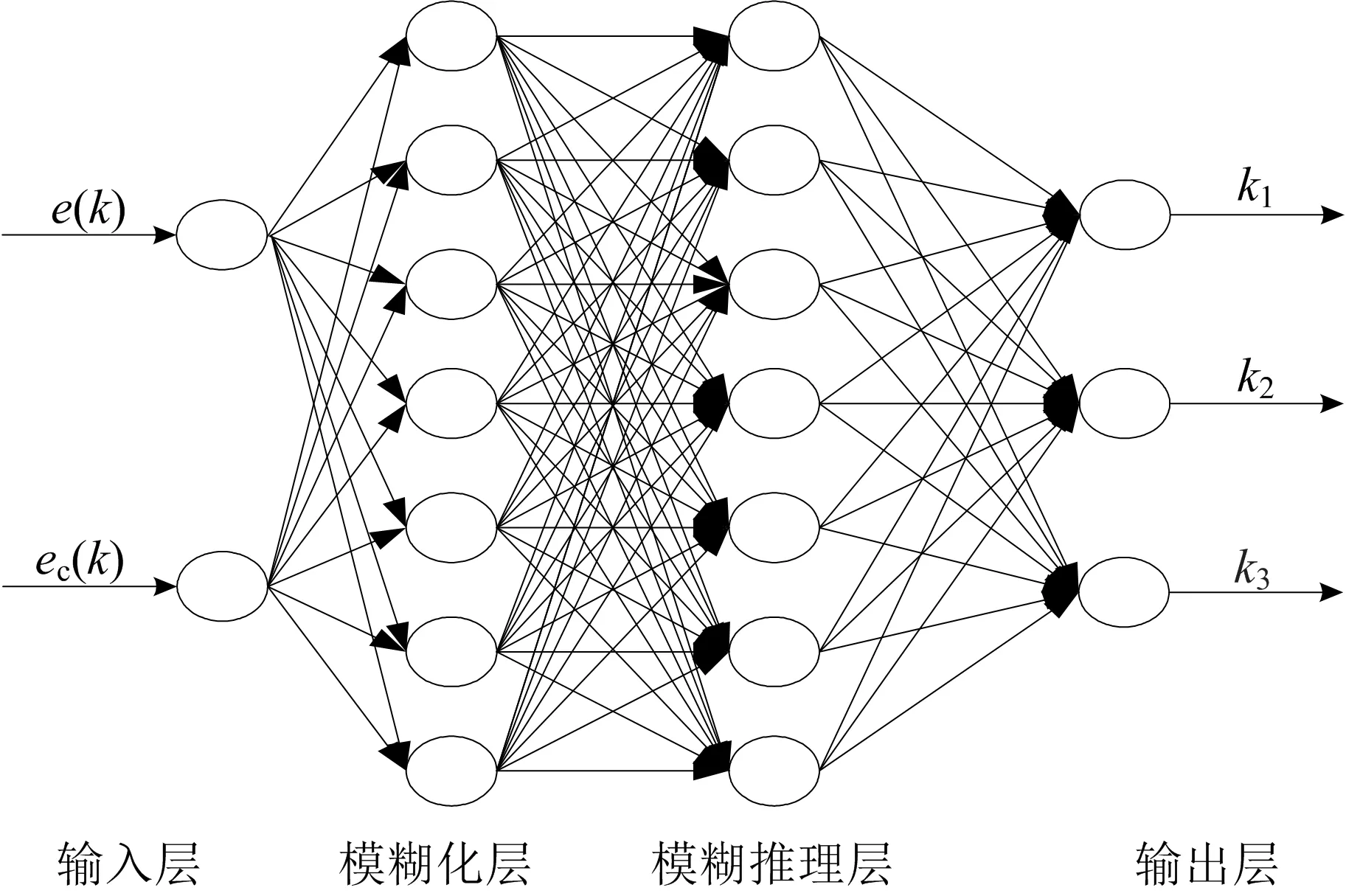
图2 DFNN控制器结构

DFNN控制器结构分为4层，各层的控制情况如下：

第1层为输入层，该层有2个节点，对应风电机组反馈的功率及转速的偏差

e

(

k

)及其变化率

e

(

k

)，将偏差及其变化率传至下层.

第2层为模糊化层(隶属函数层)，该层的7个节点对应上层的2个输出模糊化划分后得到的7个模糊集.通过相应的隶属函数，计算输入量与模糊集合间的匹配度.隶属函数的表达式为

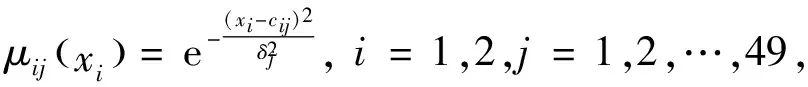
(14)

其中：

x

为输入变量，

c

为第

j

个高斯隶属函数的中心值，

δ

是第

j

个高斯隶属函数的宽度.

第3层为模糊推理层，该层有7个节点，利用

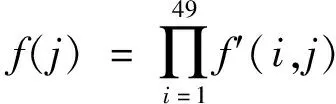
(15)

匹配输入该层的7个模糊量，得到控制的最优权重，并将其作为该层的输出值.式(15)中

f

′(

i

,

j

)为隶属函数值.

第4层为输出层，该层输出的是PID控制器的3个参数，其表达式为

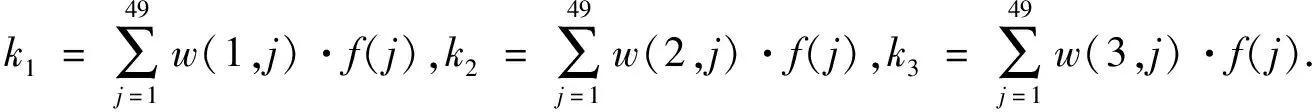
(16)

根据式(16)得到

k

，

k

，

k

，然后通过下式得到桨距角的实际值

U

(

k

)=

U

(

k

-1)+

k

k

(

e

(

k

)-

e

(

k

-1))+(

k

/

k

)·

e

(

k

)+(

k

/

k

)(

e

(

k

)-2

e

(

k

-1)+

e

(

k

-2)).

(17)

3.4 UKF-DFNN控制器

图3为UKF-DFNN控制框图.

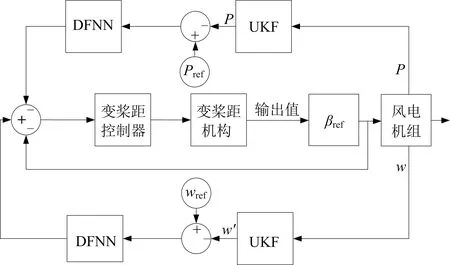
图3 UKF-DFNN控制框图

如图3所示，在模糊控制中，将上一时刻UKF预测的转速

w

(

k

-1)与当前时刻实际的转速

w

(

k

)的差值

Δw

及d(

Δw

)/d

t

作为控制器的输入，桨距角作为输出.转子转速的基本论域为[1.3 rad·s,1.7 rad·s]、模糊论域为{-3,3};转速增量

Δw

的基本论域为[-0.2 rad·s,0.2 rad·s]、模糊论域为{-3,3}；桨距角的变化范围为[-4°,4°].

k

，

k

，

k

的模糊控制规则分别如表1～3所示,其中NB，NM，NS，ZO，PS，PM，PB分别表示负大、负中、负小、零零、正小、正中、正大(“正”“零”“负”表示输入输出值的性质；“大”“中”“小”“零”表示其绝对值大小).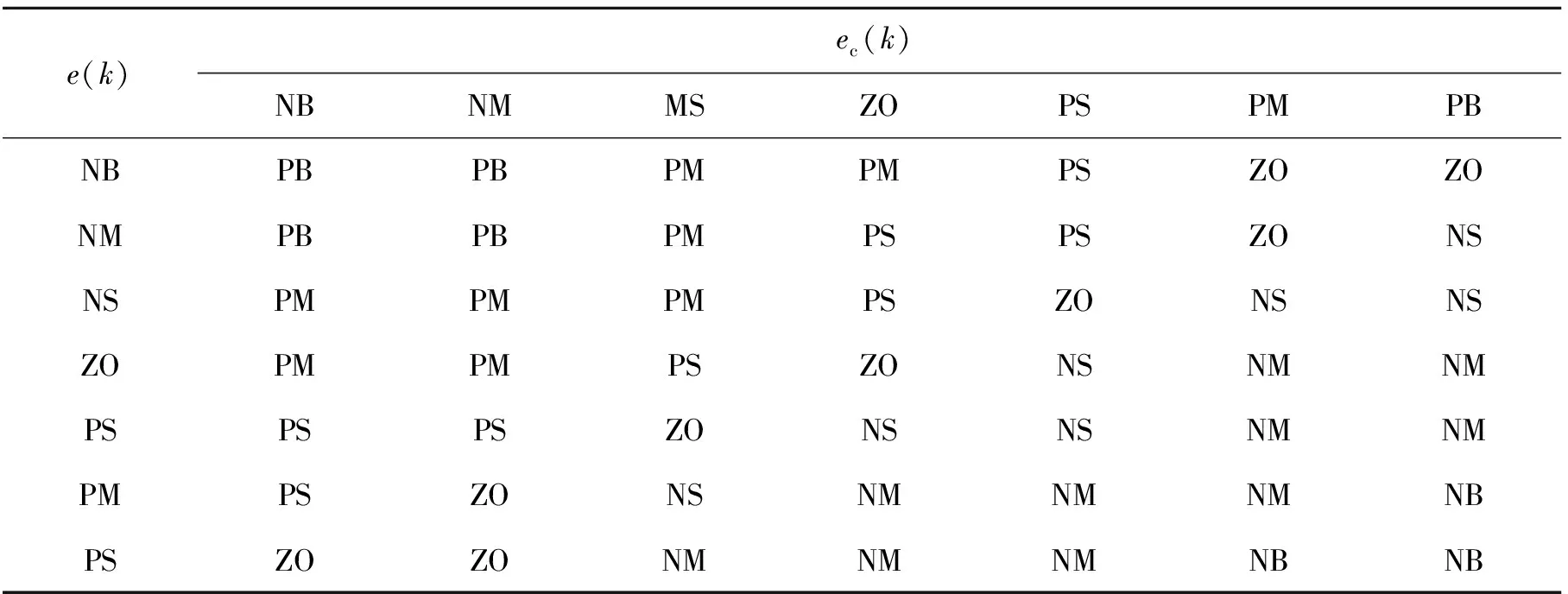

表1 k1的模糊控制规则

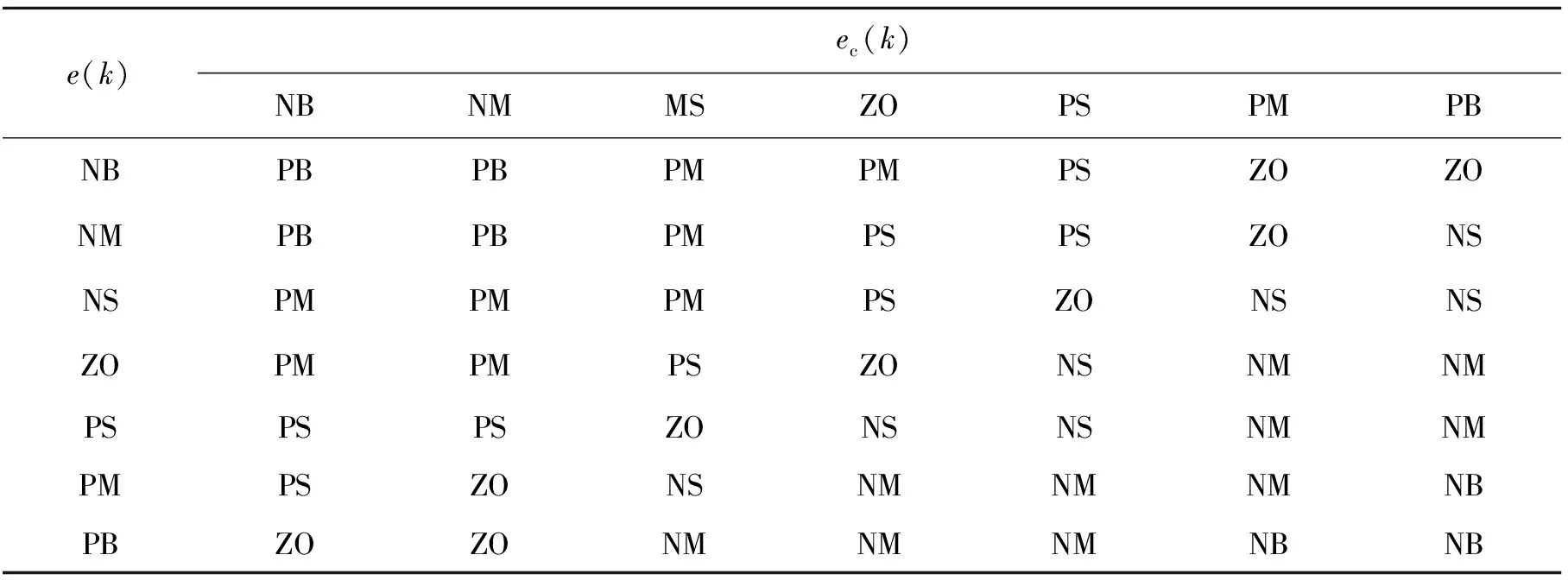
表2 k2的模糊控制规则

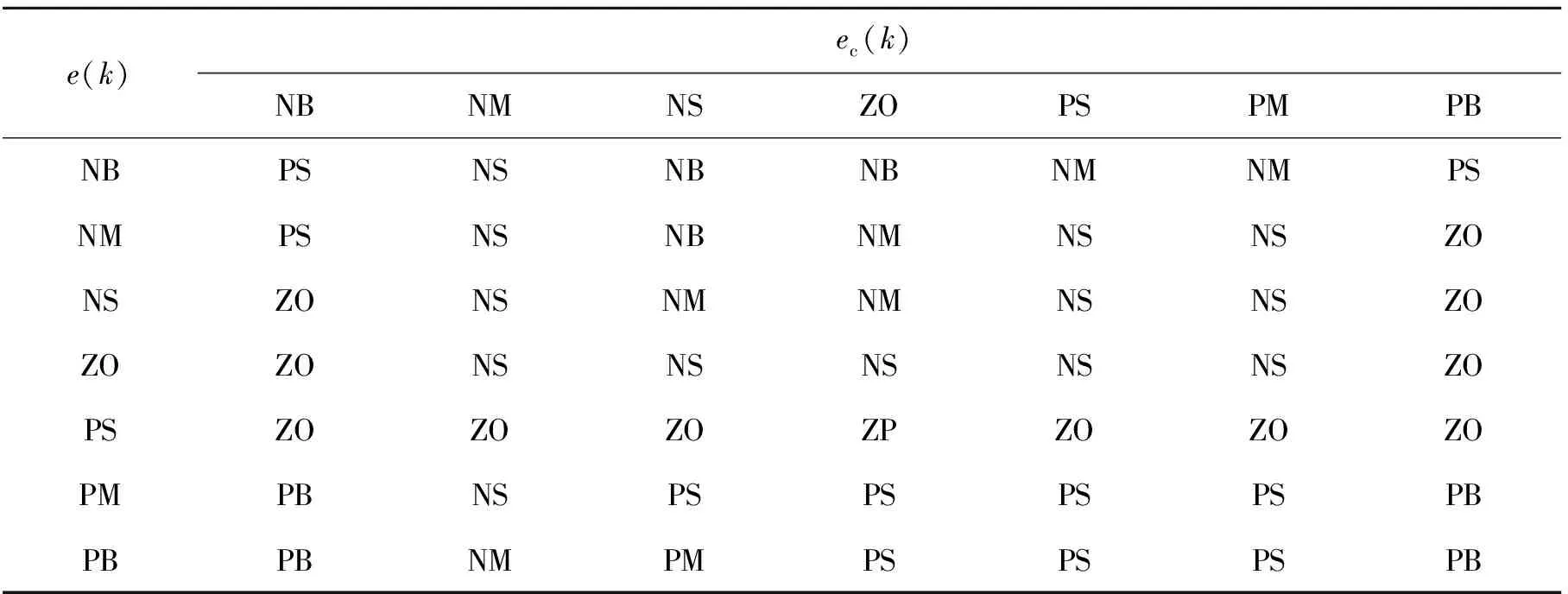
表3 k3的模糊控制规则

模糊输出的3维观测图如图4所示.

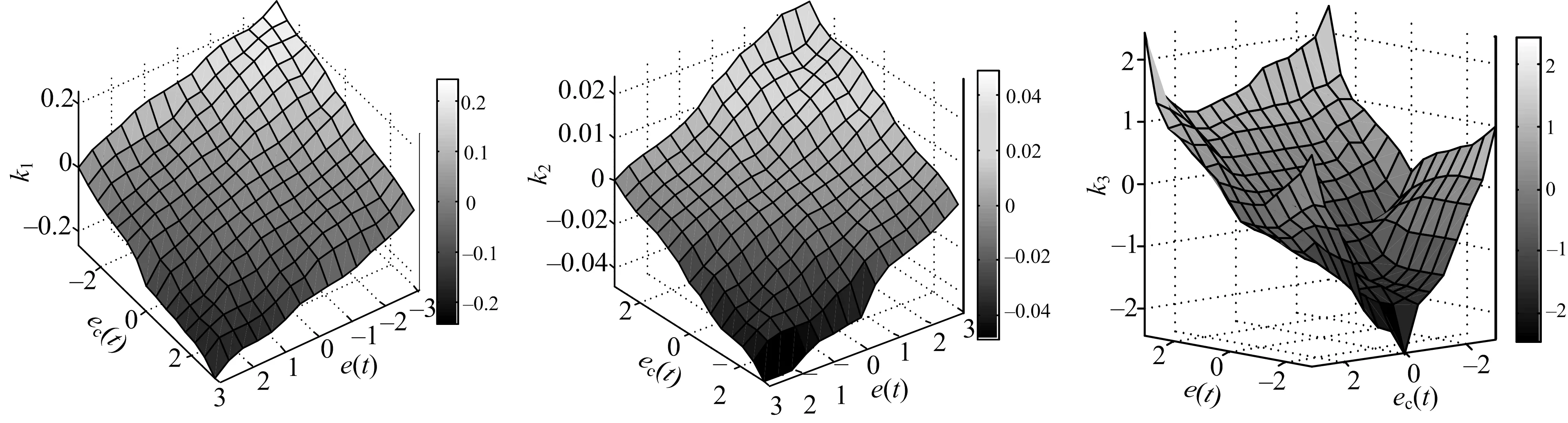
图4 模糊输出的3维观测图

4 仿真验证

该文采用Matlab/Simulink对系统进行建模仿真.在波动风速大于额定风速的情况下，对模糊PID控制、RBF神经网络控制及该文的UKF-DFNN控制策略进行仿真分析.风电机组的参数为：风轮半径

R

为40 m，额定转速

ω

为1.6 rad·s, 切入风速

V

为3 m·s，额定风速

V

为12 m·s，切出风速

V

为25 m/s,额定功率

P

为3 MW.UKF的参数设置为：

α

=0.9，

β

=2，

k

=2.基于图5给定的全风速范围的风速曲线，进行仿真验证.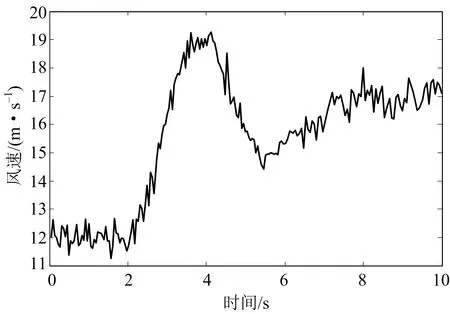

图5 风速曲线

图6，7分别为风电机组的转速预测误差、功率预测误差.由图6，7可以看出，通过UKF对风电机组反馈的转子转速及功率进行滤波修正处理，能使转子转速及功率能跟踪实际值.转速误差不到额定转速的1%，功率误差为额定功率的3%，与未修正的相比，二者的误差显著减小，有效消除了系统误差.

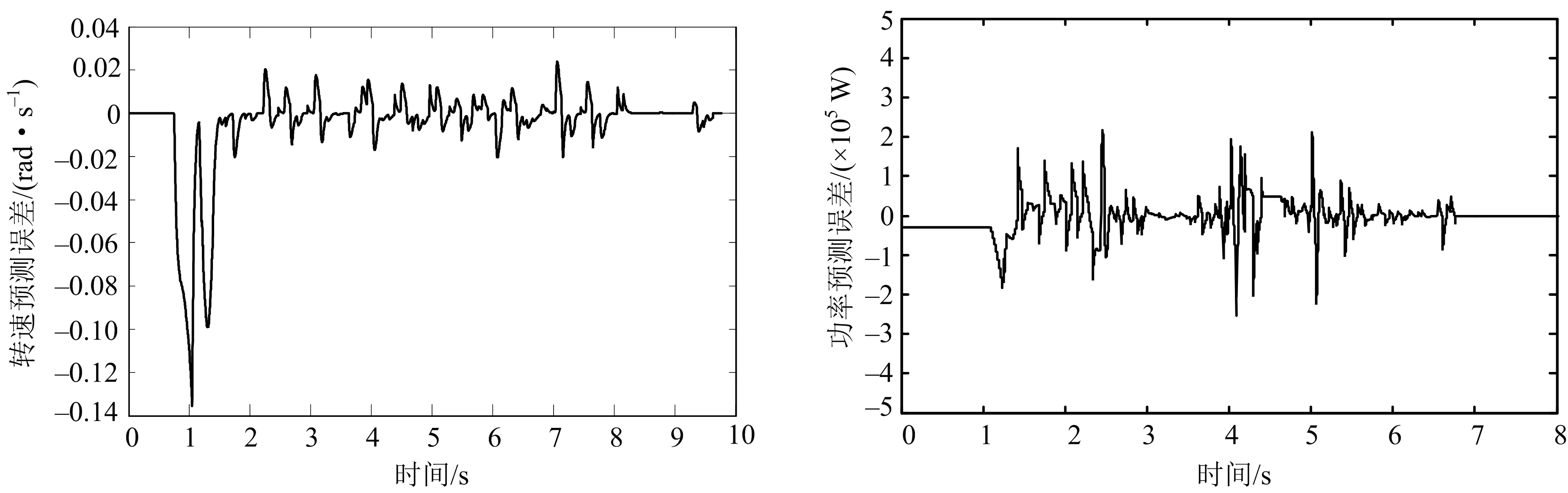
图6 转速预测误差 图7 功率预测误差

在Matlab/Simulink中运行仿真模型，得到不同控制下的风电机组桨距角、风能利用系数及输出功率的变化曲线，如图8～10所示.

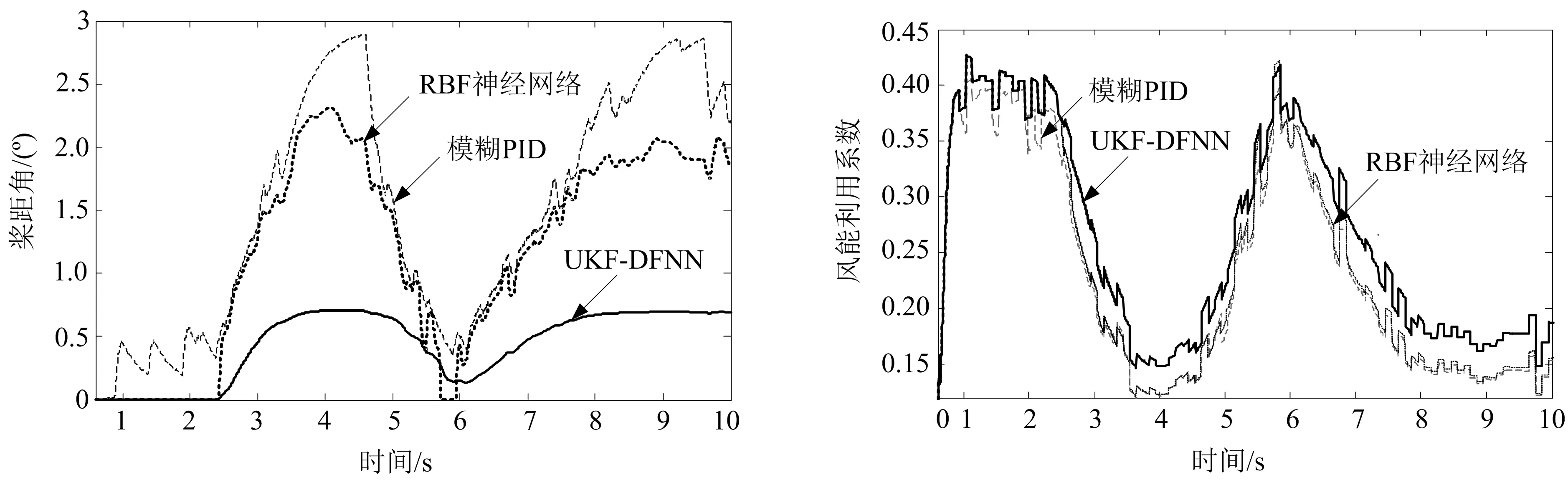
图8 不同控制下的桨距角变化曲线 图9 不同控制下的风能利用系数变化曲线

由图8可知:采用模糊PID,RBF神经网络控制时，桨距角波动均比较大；采用UKF-DFNN控制时，相对前两者桨距角波动小，且在7 s后风速小范围波动的工况下，桨距角波动更小，能维持稳定，这是因为UKF-DFNN控制能有效补偿网络传输时延.

由图9可知: UKF-DFNN控制跟踪风能利用系数的性能比另外两者好；当风速变化时，UKF-DFNN控制能快速感知并实时调整桨距角，进而改变风能利用系数.

模糊 PID及RBF 神经网络控制，以风速作为控制量输入，而UKF-DFNN控制将发电机功率和转子速度共同作为控制量输入.图10的结果表明：模糊PID及RBF神经网络控制不能很好地将发电机功率保持在额定值，且有较高的纹波分量；UKF-DFNN控制的输出功率在额定功率附近波动，稳定性更好.

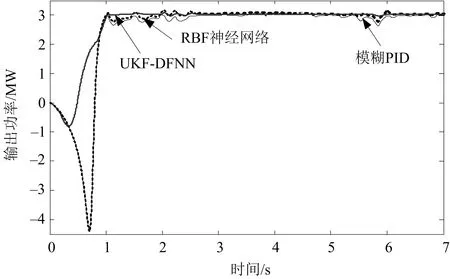
图10 不同控制下的输出功率变化曲线

5 结束语

笔者针对风电机组在风速波动的情况下出现的转子转速及功率的波动问题，提出了基于UKF-DFNN的控制策略.该策略利用UKF对反馈的转子转速及功率进行滤波处理，利用DFNN对滤波后的数值进行模糊整定，能快速精确调节PID的参数.仿真结果表明：该控制策略能有效抑制桨距角的波动，并减小桨距角及输出功率的超调量，使风速大于额定风速时风电机组的输出功率维持在额定功率附近，增强了系统的稳定性；同时，可减少桨距角变化带来的变桨距系统的频繁启停，延长了风机的使用寿命.