基于度量核和GHI核混合的植物叶片识别算法

张东明，李新华*，梅星宇，张东彦

(1.安徽大学 农业生态大数据分析与应用技术国家地方联合工程研究中心，安徽 合肥 230601；2.安徽大学 电子信息工程学院，安徽 合肥 230601)

植物叶片识别是植物保护的基础，而传统人工识别方法耗时耗力、主观性强、易出错，因此利用计算机视觉技术自动识别植物叶片就显得尤为重要.迄今为止，研究人员在这一领域做了很多工作.文献[1]构造多尺度距离矩阵(multiscale distance matrix，简称MDM)形状特征用于植物叶片识别.文献[2]提出了一种新的特征描述符，名为多尺度曲率直方图(histogram of curvature over scale，简称HoCS)，将其用于植物叶片识别.文献[3]在文献[2]的基础上，融合HoCS形状特征和局部二值模式(local binary pattern，简称LBP)纹理特征，利用K最近邻(k-nearest-neighbor，简称KNN)方法识别叶片.文献[4]提取叶片图像几何特征及Hu不变矩特征，利用支持向量机(support vector machine, 简称SVM)分类器进行叶片识别.文献[5]经翻转、缩放等操作增广叶片数据集后，利用迁移学习对植物叶片进行识别.文献[6]将经主分量分析(principal components analysis，简称PCA)降维后的LBP特征与形状特征结合，利用KNN识别植物叶片.文献[7]提出一种基于词袋(bag of words，简称BOW)模型和熵序列的叶片识别方法.文献[8]将叶片分为2或4个部分，提取各部分的颜色、纹理特征，利用极限学习机(extreme learning machines，简称ELM)对叶片进行识别.文献[9]首先利用小波分解出叶片高低频信息，然后分别对高低频信息提取LBP及局部向量化(local phase quantization，简称LPQ)特征，最后利用KNN识别叶片.

植物叶片识别首先是特征提取及降维，然后将最终特征送入分类器进行识别，因此获得高辨识度的图像特征和高性能分类器是提高叶片识别率的关键.为了得到更高的植物叶片识别率，该文提出基于度量核和GHI核混合的植物叶片识别算法.构建多尺度边缘轮廓(multi-scale marginal contour，简称MMC)算子，然后提取MMC形状特征、LBP空域纹理特征、LPQ频域纹理特征，最后将这些特征组合为复合特征.利用度量学习和马氏距离改造负距离核构建度量核，再将其与广义直方图交叉(generalized histogram intersection，简称GHI)核加权融合形成组合核.通过仿真实验验证算法的可行性.

1 图像预处理

植物叶片预处理流程如图1所示.将原始RGB图像转换成HSV图像，利用最近邻插值算法将图像分辨率调整到400×300；提取图像的V分量；采用中值滤波器去噪，利用K-means算法对V分量进行分割，得到二值图像；将二值图像与缩放后的原图卷积得到前景图，便于后期提取形状和纹理特征.

图1 植物叶片预处理流程

2 特征提取

为了提高识别率，该文构建了具有旋转不变性和尺度不变性的MMC算子.分别提取MMC形状特征、LBP空域纹理特征、LPQ频域纹理特征，然后将这些特征组合为具有高辨识度的复合特征.

2.1 MMC形状特征

图2为MMC形状特征提取示意图，其中蓝色点为采样后得到的轮廓点，绿色矩形为最小外接矩形，

O

为最小外接矩形的中心，

P

,

P

为相邻的两个轮廓点.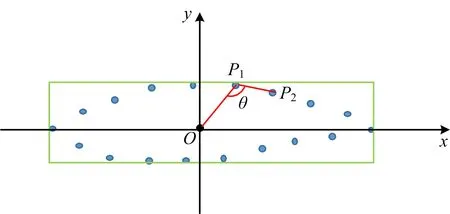

图2 MMC形状特征提取示意图

MMC形状特征提取的步骤为：

(1)对预处理后图像，用sobel算子提取轮廓Boundary，移动整个轮廓使最小外接矩形的中心为原点，等间隔抽取200个点，形成轮廓描述点集Edges={

P

,

P

…，

P

}.(2)计算角度

θ

=∠

OP

P

+1及原点

O

与当前边界点

P

间的欧式距离

r

=

d

(

O

,

P

).

(3)重复(2)，直至点集中所有点处理完毕.

(4)利用最大距离

r

，对所有距离

r

进行归一化处理.分别将

r

，

θ

分为10，12个等级，得到

r

-

θ

直方图.(5)加入多尺度特征，尺度取值为{1,2,…,

k

,

k

+1,…,

n

}，其中

n

为最大尺度且

n

>1，尺度

k

的角度

θ

=∠

OP

P

+4，重复(2)～(4).所有尺度特征计算结束后，将所有尺度特征组合为MMC形状特征.

2.2 LBP空域纹理特征

LBP是由Ojala 等提出的一种纹理特征算子.在一个3×3的窗口，以窗口中心像素为阈值，依次比较窗口中其他像素与中心像素的大小，若其他像素大于等于中心像素，则记为1，否则记为0.将结果按顺序排列，得到一个8位的二进制数，其对应的十进制值就是该中心像素的LBP特征值.LBP特征值的数学表达式为

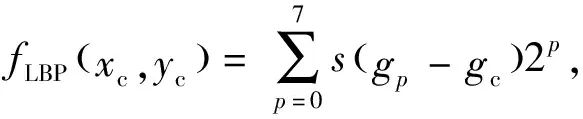
(1)

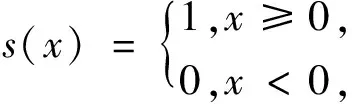
(2)

其中：

g

为邻域像素的灰度值，

g

为中心像素的灰度值，(

x

,

y

)为窗口中心坐标.

2.3 LPQ频域纹理特征

LPQ是另一种常用的纹理特征算子.在图像

f

(

x

)中，对任意像素点

x

的

M

×

M

邻域

N

，通过离散的短时傅里叶变换得到相应的邻域相位.在邻域

N

上，短时傅里叶变换为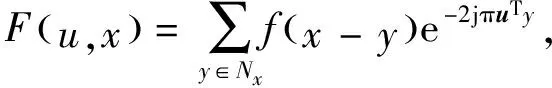

(3)

其中：

y

为

N

中的邻域坐标，为频率.通过4个频率=[

a

,0]，=[0,

a

]，=[

a

,

a

]，=[

a

,-

a

]得到傅里叶系数，其中

a

的值很小，且满足

H

(

u

)>0.傅里叶系数

F

的计算公式为

F

=[Re{

F

(

u

,

x

)},Re{

F

(

u

,

x

)},…,Re{

F

(

u

,

x

)},Im{

F

(

u

,

x

)},Im{

F

(

u

,

x

)},…,Im{

F

(

u

,

x

)}].

(4)

傅里叶系数的相位由实部和虚部的符号确定，即

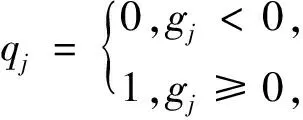
(5)

其中：

g

是

F

的第

j

部分.按顺序对

q

进行二进制编码，得到该像素点的LPQ特征值为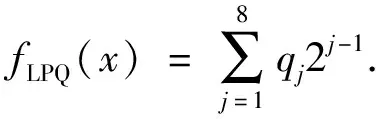

(6)

3 分类器的构造

在植物叶片图像识别中，量度不同样本间的相似性是其中的一个关键环节.GHI核适用于直方图特征，但仅考虑了直方图的整体特征.度量学习能挖掘不同维特征间的内在联系，所以该文利用度量学习和马氏距离改造负距离核形成度量核.但是度量核忽略了直方图的整体特征，为了兼顾直方图的整体特征和不同维特征间的内在联系，该文将度量核和GHI核加权融合.

3.1 度量学习

马氏度量学习是度量学习的一个重要分支，其针对的是线性度量学习.设,为两个样本的特征向量，用

Δ

=,描述两特征向量间的差异.设

Ω

(

y

=

y

)为相同类别叶片图像间的内部差异，

Ω

(

y

≠

y

)为不同类别叶片图像间的类间差异.利用KISSME和贝叶斯人脸方法，得到样本,间的马氏距离为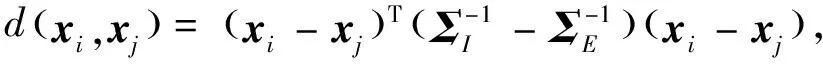

(7)

其中：，分别为

Ω

,

Ω

的协方差矩阵.通过投影矩阵=(,,…,)，将原始样本特征,投影到新的特征空间，得到,间的马氏距离为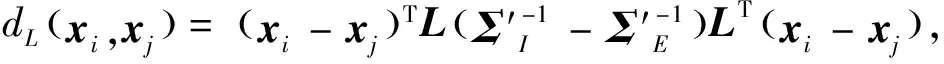

(8)

其中：′=,′=.特征投影到子空间后，通过优化投影方向使

σ

()/

σ

()最大化.将

σ

()/

σ

()最大化转化为如下的广义瑞利熵最大化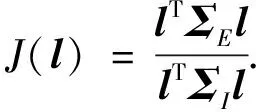

(9)

J

()的最大化等价于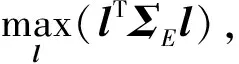

使得

=1.

(10)

投影矩阵可通过线性判别分析(linear discriminant analysis, 简称LDA)中的广义特征值分解方法得到.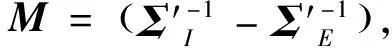

d

(,)=(-)(-).

(11)

3.2 基于度量核和GHI核混合的SVM分类器

将

d

(,)代替负距离核中的欧式距离，得到该文构建的度量核函数为

K

(,)=-

d

(,).

(12)

GHI核由Boughorbel提出，适用于直方图特征分类，其核函数为

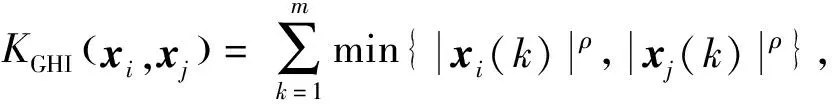
(13)

其中：

ρ

≥0为超参数，用于优化核函数.利用式(12)，(13)构建的组合核为

K

(,)=(

λ

/

m

)

K

(,)+[(1-

λ

)/

m

]

K

(,)，

(14)

其中：

λ

为融合系数(0.1≤

λ

≤0.9)；m,m分别为

K

,

K

在训练集上的核矩阵元素的最大绝对值.将

K

(,)代入SVM的决策函数，得到分类器的决策函数为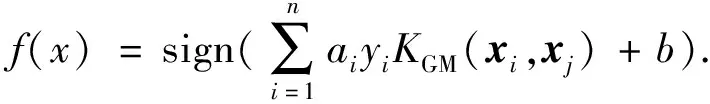

(15)

4 基于度量核和GHI核混合的植物叶片识别算法

图3为叶片识别流程.首先，数据集划分为训练集和测试集；其次，对预处理后的叶片图像提取MMC形状特征、LBP纹理特征、LPQ纹理特征，进而将它们组合为复合特征；再次，通过迭代寻优，确定GHI核和度量核的融合系数，构造组合核SVM分类器；最后，通过组合核SVM分类器，对输入叶片的复合特征进行识别，得到叶片识别结果.

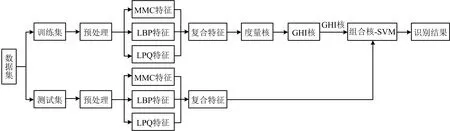
图3 叶片识别流程

基于度量核和GHI核混合的植物叶片识别算法的具体步骤为：

(1)对预处理后的单个叶片图像进行处理得到灰度图

G

，将

G

分成2×2块，可得到

G

=[

G

,

G

,

G

,

G

].利用

G

求出LBP特征

Q

=[

q

,

q

,

q

,

q

]和 LPQ特征

P

=[

p

,

p

,

p

,

p

].通过

G

获取轮廓

C

，利用

C

求出MMC特征

S

.拼接3个特征得到复合特征

W

=[

S

,

Q

,

P

].

(2)针对所有叶片图像，重复步骤(1)，得到训练集样本特征和测试集样本特征.

(3)通过训练集样本数据求得投影矩阵，利用得到

d

，进而构建度量核函数

K

.(4)将GHI核函数超参数

ρ

设为0.5，将组合核融合系数

λ

的初始值设为0.1.通过GHI核和度量核在训练集上得到对应的核矩阵，进而得到两个核矩阵元素的最大绝对值

m

,

m

.(5)通过

m

,

m

和融合系数

λ

构建组合核函数

K

.利用训练集训练分类器，得到决策函数

f

(

x

).通过测试集得到识别结果.

5 仿真实验及其结果

为了验证所提算法的可行性，在Win10操作系统下，使用MATLAB 2016a和 Libsvm工具箱进行实验.实验叶片图像源自Flavia数据集，Flavia数据集由Wu等制作，包含32种植物的叶片图像，总计1 907张，所有物种的叶片图像数量均超过50张，叶片图像大小为1 600×1 200.图4为数据集图像示例.该文选取数据集物种图像的70%作为训练集，剩下的作为测试集.将5次实验识别率的平均值作为最终识别率.组合核函数融合系数

λ

设为0.6.

图4 数据集图像示例

表1给出了不同特征的识别率.从表1可看出：该文构建的MMC形状特征的识别率明显高于MDM，HoCS形状特征的，其值达到了90.45%，说明给文构建的MMC形状特征是有效的；复合特征的识别率比单独的形状或纹理特征的高很多，其值达到99.31%，说明该文构建的复合特征有更高的识别率.

表1 不同特征的识别率 %

图5给出了不同核函数的复合特征识别率.从图5可看出：与常用的线性核、多项式以及高斯核相比，GHI核及度量核识别效果更好，二者的识别率分别为98.11%和98.22%；度量核与GHI核组合成的混合核的识别率最高，达到了99.31%，说明混合核能够更全面、更准确地度量样本间的相关性.

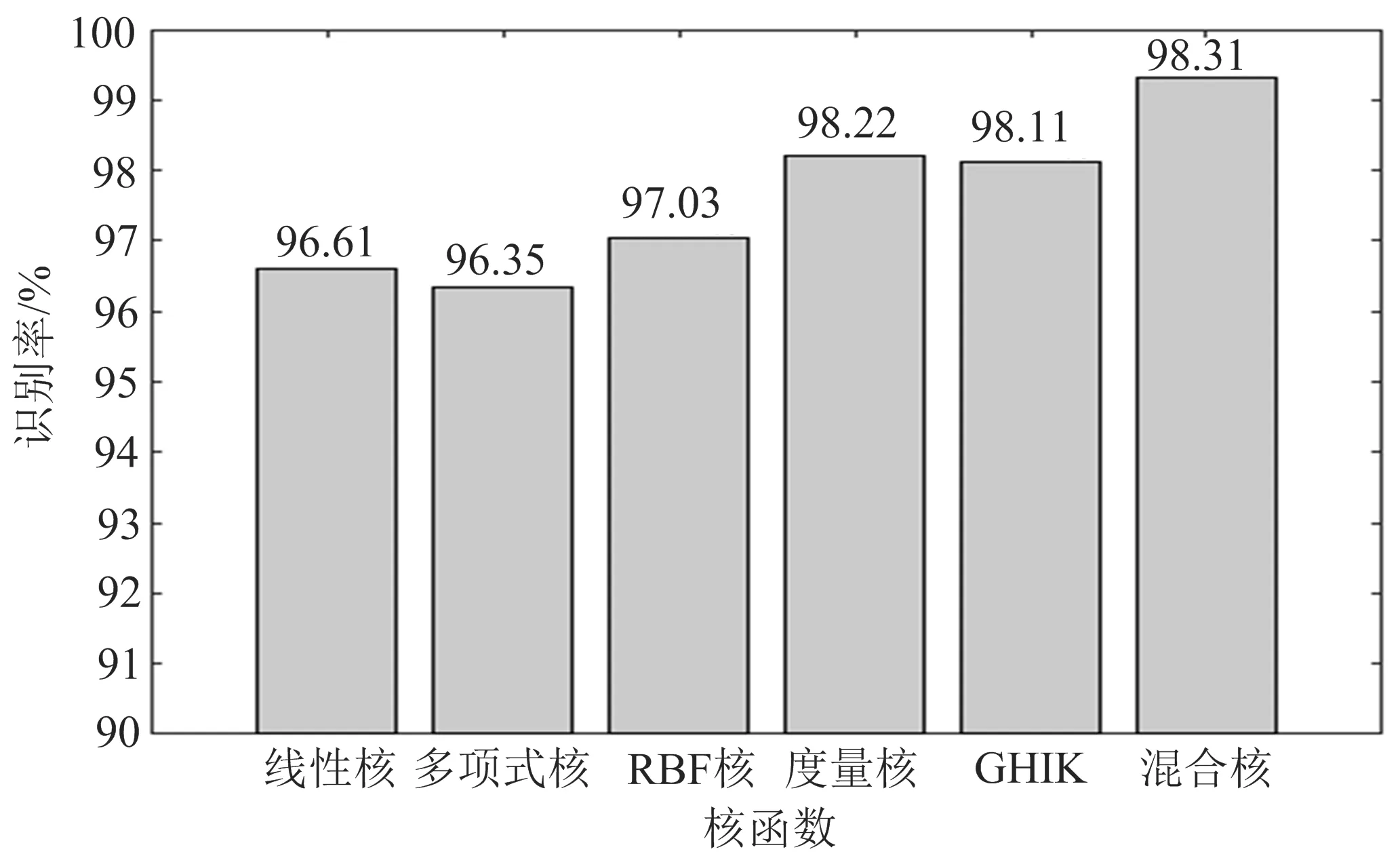
图5 不同核函数的复合特征识别率

表2展示了该文算法与其他文献算法的复合特征识别率比较.由表2可知，相对于其他文献算法，该文算法的识别率最高.

表2 不同算法的复合特征识别率比较 %

表3为该文算法各类植物叶片的复合特征识别率.从表3中可看出，桂花、木莲、三叉戟枫存在误识别情况.

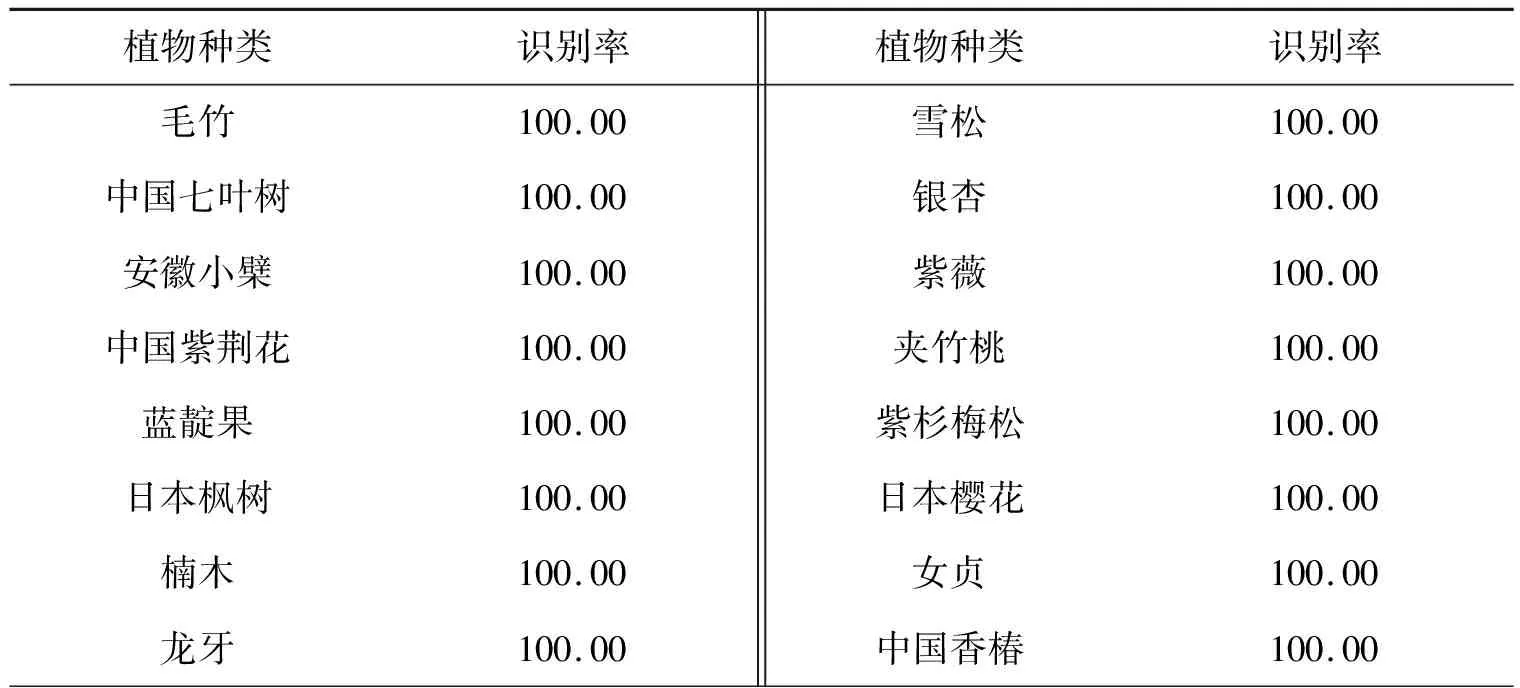
表3 该文算法各类植物叶片的复合特征识别率 %

表4为误识别情况统计，其中桂花2次被识别为樟树，木莲1次被识别为夹竹桃，三叉戟枫1次被识别为鹅掌楸.桂花和樟树叶片形状相似，二者均为不规则的椭圆、两端较尖、纹理相似、表面平滑，因此会出现误识别.木莲和夹竹桃的形状均呈现梭形，形状差异较小，纹理虽存在一定的差异，但总体来说相似度较高，因此也会出现误识别.三叉戟枫与鹅掌楸的形状差距较大，正常情况下不应该出现误识别，但这两种叶片的最小外接矩形端点对应的轮廓不固定，旋转后叶尖朝向也不固定，导致纹理特征相似度很高，从而出现误识别.

表4 误识别情况统计

6 结束语

为了充分利用叶片直方图的整体特征以及不同维特征间的内在联系，该文提出了基于度量核和GHI核混合的植物叶片识别算法.构建了MMC形状特征，然后融合 MMC，LBP，LPQ特征，得到具有高辨识度的复合特征.利用度量学习和马氏距离改造负距离核构建度量核，将度量核和GHI核加权融合形成组合核.构造组合核SVM分类器，对输入叶片的复合特征进行识别.仿真实验结果表明：相对于其他算法，该文算法具有较高的识别率.该文构建的组合核函数是针对直方图特征设计的，后续研究可考虑改进组合核函数，使其更好地适用于多种类型特征的叶片识别.