双调和映射的α阶全星形性与全凸性
2021-03-20 02:25龙波涌王麒翰
安徽大学学报(自然科学版) 2021年2期
龙波涌,许 灵,王麒翰
(安徽大学 数学科学学院, 安徽 合肥 230601)

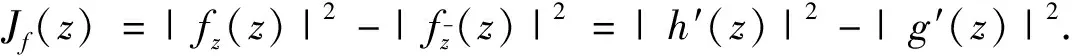


F
(z
)=|z
|G
(z
)+H
(z
),(1)

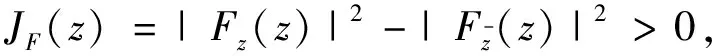



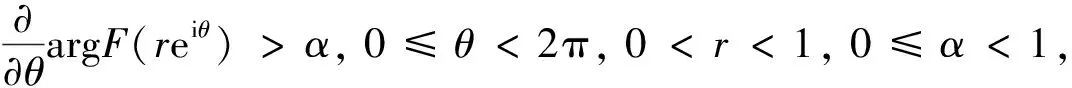
F
关于原点是α
阶全星形的.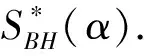

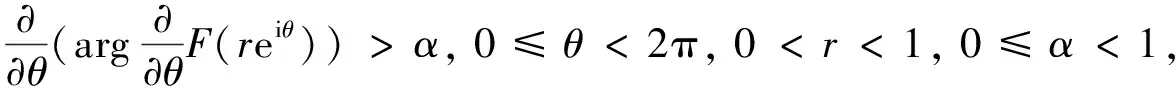
F
是α
阶全凸的,记F
∈K
(α
).特别地, 若α
=0, 那么F
是全凸的, 即F
∈K
.对于β
>1,A
的子类M(β
)和N(β
)分别定义为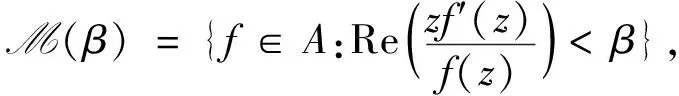
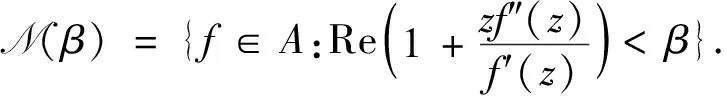
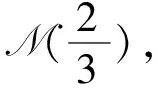

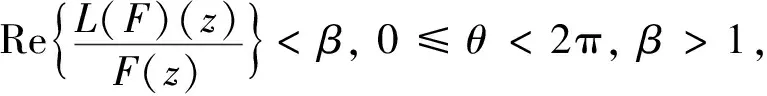
F
(z
)属于双调和映射类M(β
).这里,L
为线性复算子,被定义为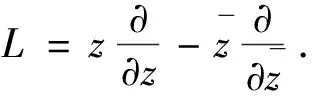

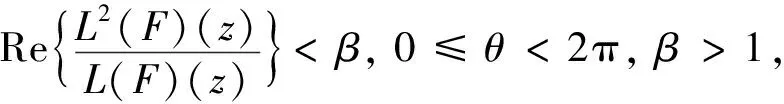
F
(z
)属于双调和映射类N
(β
).注意到, 文献[7]中研究了线性复算子L
的相关性质, 其中F
∈C
.算子L
保调和和双调和性, 并给出如下引理.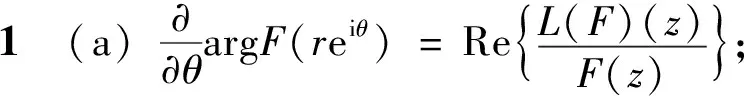
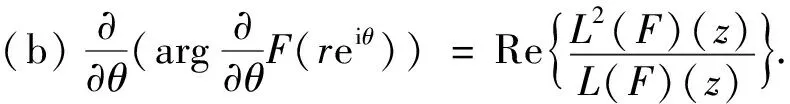


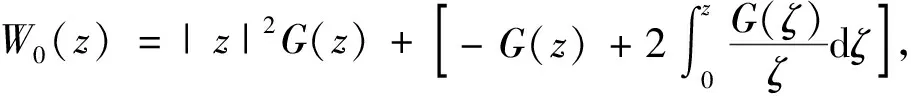
(2)

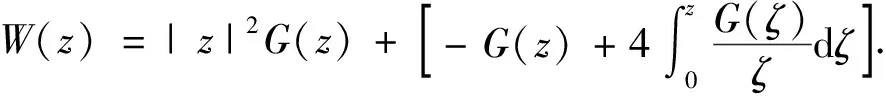
(3)
不过, 文献[8]的结尾提出了如下的一个非常有趣的问题.
问题
若G
∈S
, 那么W
(z
)的单叶半径是多少?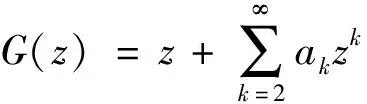
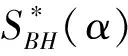
1 系数不等式
为了证明后面的定理, 需要下面两个引理.
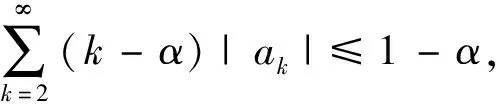
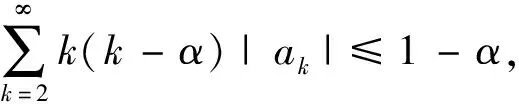
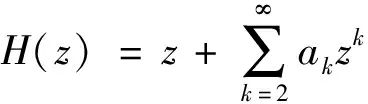
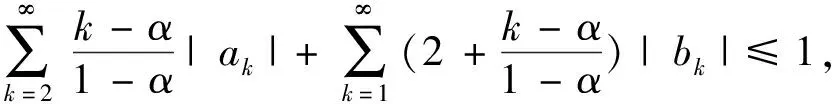
(4)

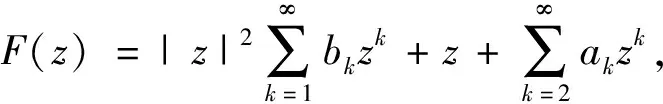
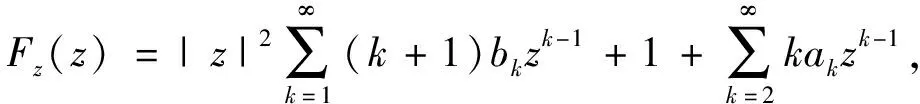
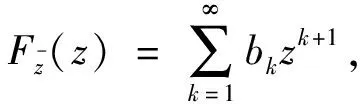
所以,有
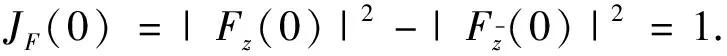
z
≠0,有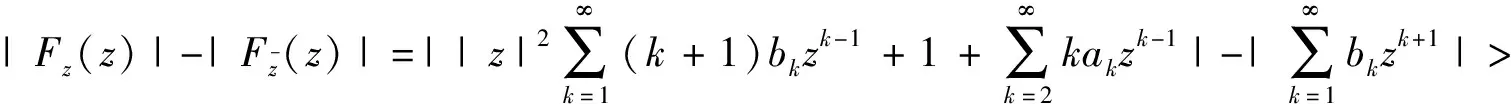

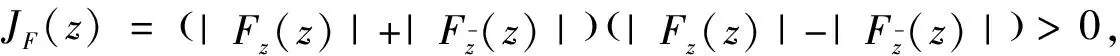
r
∈(0,1),设F
:=r
G
(z
)+H
(z
),(5)
则
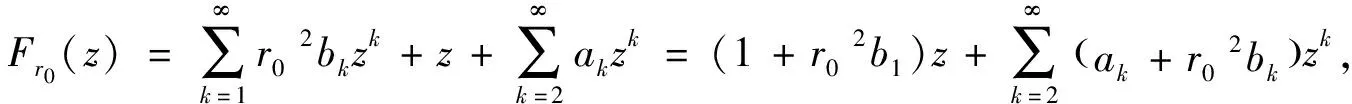

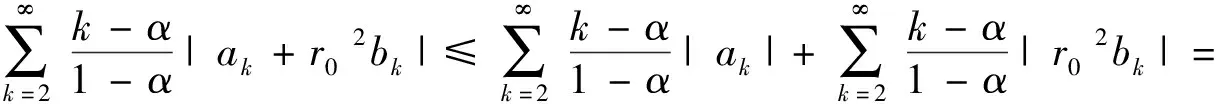
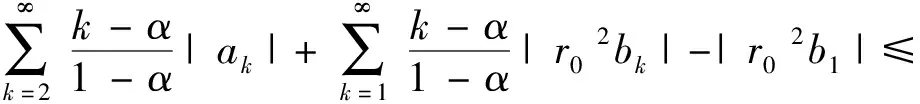
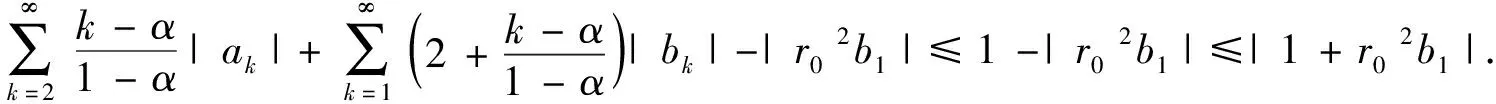
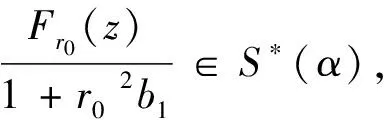
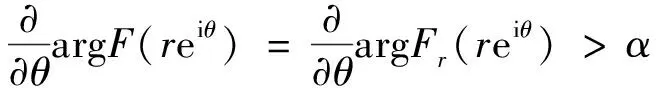
(6)
对每个z
=r
ei≠0都成立, 且F
在每个|z
|=r
上都单叶.
注1
当α
=0时, 定理1与文献[19]中的引理6是一致的.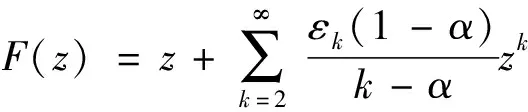
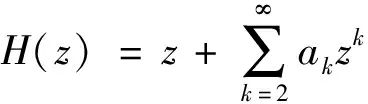
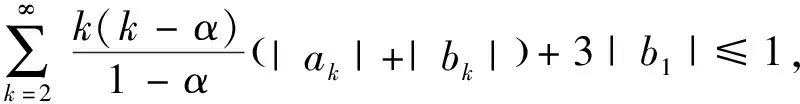
(7)

证明
保向性的证明与定理1类似.其中, 当z
≠0时,有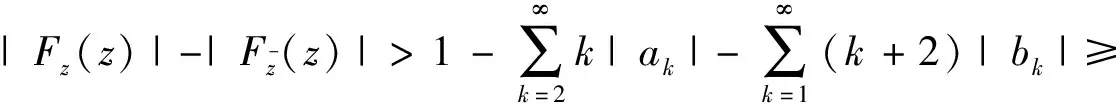
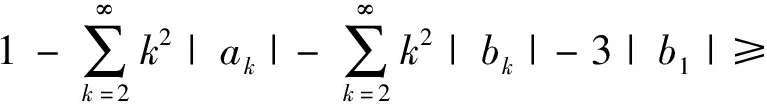
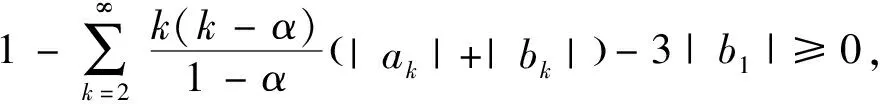
从而,有
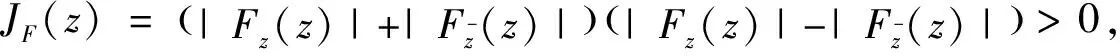


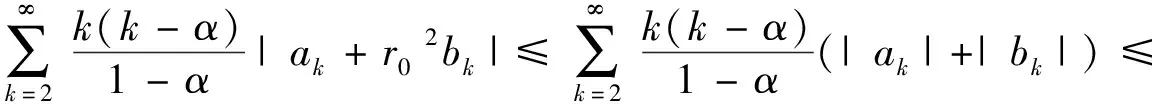
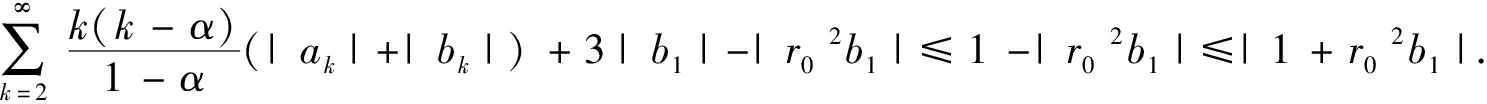
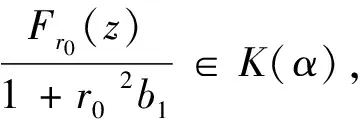
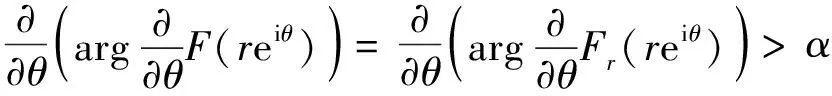
(8)
对每个z
=r
ei≠0都成立, 且F
在每个|z
|=r
上都单叶.
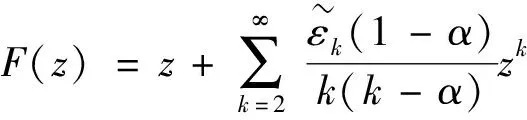
2 双调和映射的两个子类
首先给出下面两个引理.
引理4
若双调和映射F
(z
)满足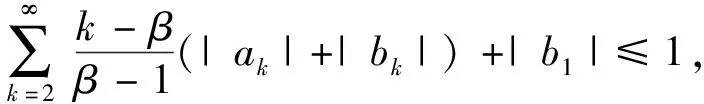
(9)
其中:1<β
≤3/2, 则F
(z
)∈M(β
).引理5
若双调和映射F
(z
)满足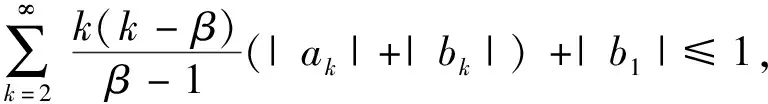
(10)
其中:1<β
≤3/2, 则F
(z
)∈N(β
).下面研究双调和映射类M(β
)和N(β
)中满足上面两个不等式的函数的星形性和凸性.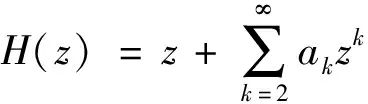
证明
由定理1知, 若双调和映射F
满足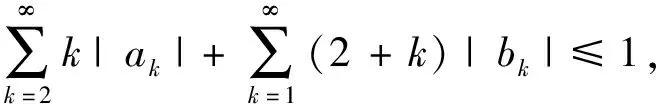


(11)
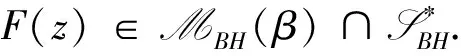
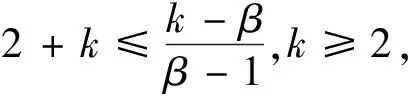
β
满足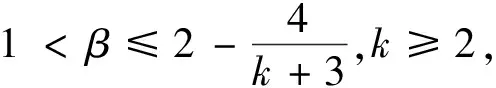
β
≤6/5.由定理2知若双调和映射F
满足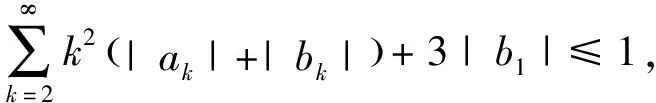

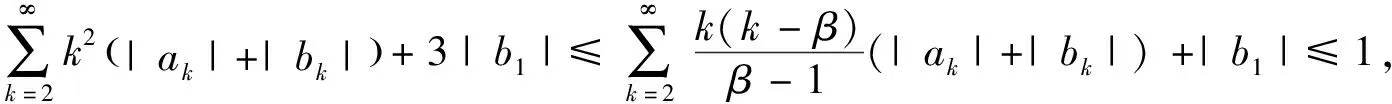
b
=0.有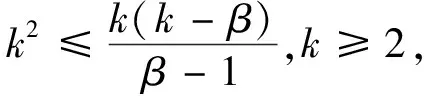
β
满足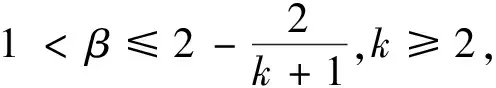
β
≤4/3.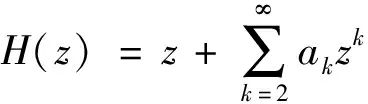
证明
对于1<β
≤3/2, 0≤α
<1, 由定理1和引理4知, 要找到最小的α
满足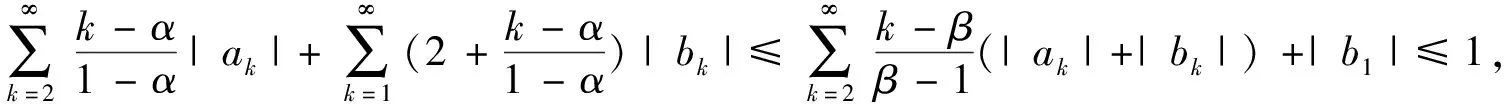
b
=0.即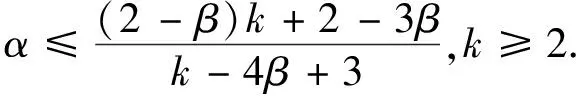
(12)
注意到(12)式的右边关于k
是递增的, 有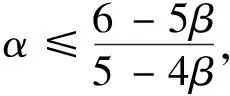
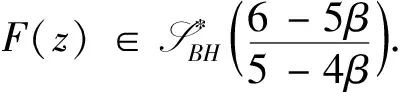
α
满足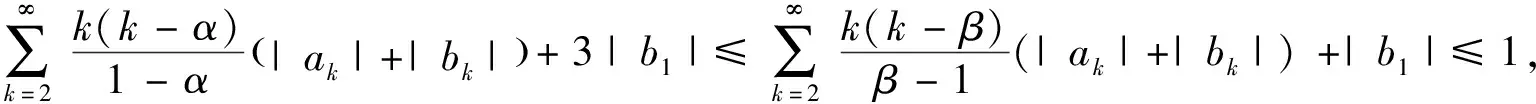
b
=0.即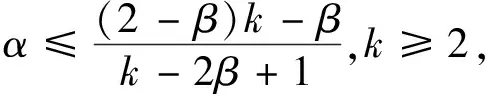
从而有
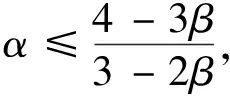
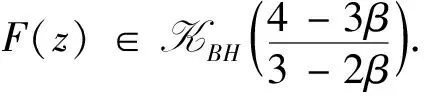
3 半径问题
首先给出几个等式
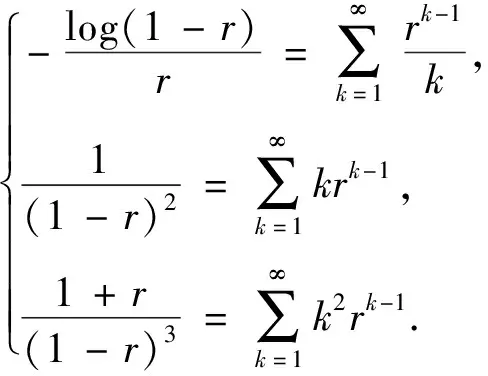
(13)
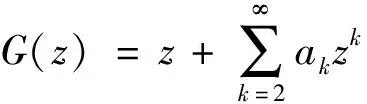
α
)r
+(2α
-10)r
+(3α
-5)r
+(15-11α
)r
+(11α
-13)r
+3-3α
=0在(0,1)内的唯一根.
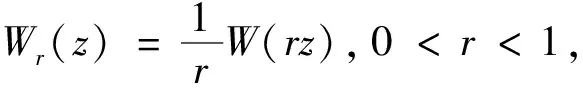
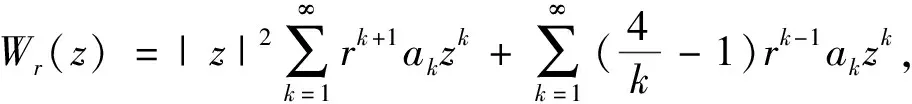
由定理1, 考虑
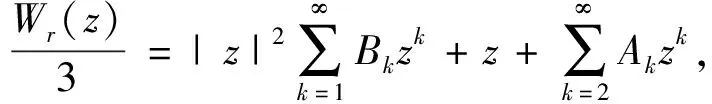
其中
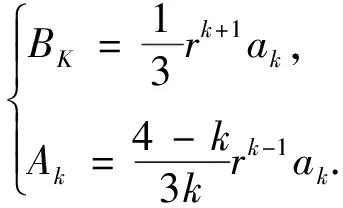
(14)
注意到W
在|z
|<r
内单叶且α
阶全星形当且仅当W
在|z
|<1内单叶且α
阶全星形.考虑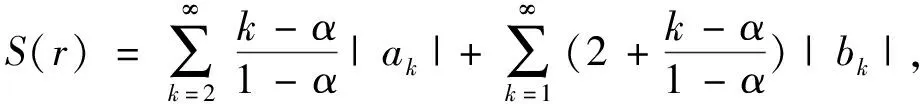
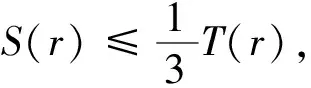
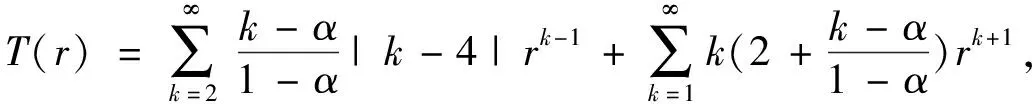
S
(r
)≤1, 即证T
(r
)≤3.结合(13)式, 有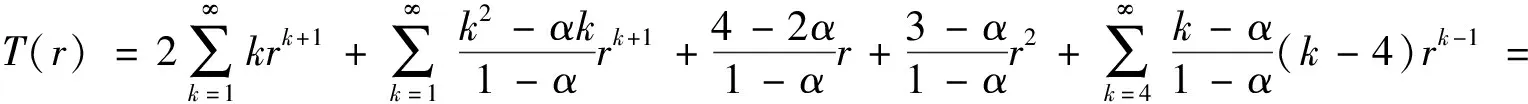
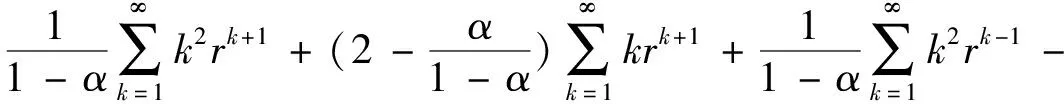
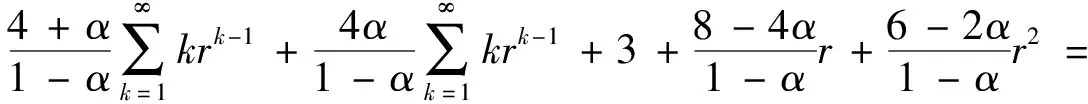
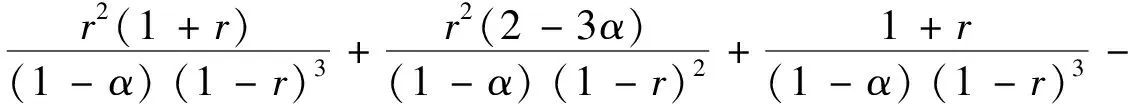
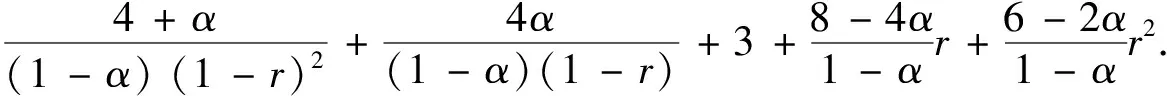
(15)
将不等式T
(r
)≤3两边同时乘以(1-α
)(1-r
), 整理得Φ
(r
)≥0,其中Φ
(r
)=(6-2α
)r
+(2α
-10)r
+(3α
-5)r
+(15-11α
)r
+(11α
-13)r
+3-3α
.(16)
因为Φ
(0)=3-3α
>0且Φ
(1)=-4<0, 所以方程Φ
(r
)=0在(0,1)内存在r
(α
), 使得当0<r
≤r
时,Φ
(r
)≥0, 从而S
(r
)≤1成立.从而由定理1知,W
(z
)在|z
|<r
内是单叶且α
阶全星形的.下证r
(α
)是方程Φ
(r
)=0在(0,1)内的唯一根.对(16)式求导并整理, 得到Φ
′(r
)=g
(r
)+αh
(r
), 其中g
(r
)=30r
-40r
-15r
+30r
-13,h
(r
)=-10r
+8r
+9r
+-22r
+11.计算可知, 对r
∈(0,1), 恒有g
(r
)<0,(17)
h
′(r
)=-40r
+24r
+18r
-22<0,所以h
(r
)在(0,1)单调递减, 又h
(0)=11>0,h
(1)=-4<0, 所以存在唯一ζ
∈(0,1),使得h
(r
)=0.下面分两种情况考虑.情形1
r
∈(0,ζ
).此时h
(r
)>0, 有Φ
′(r
)=g
(r
)+αh
(r
)<g
(r
)+h
(r
)=20r
-32r
-6r
+8r
-2.计算知对任意r
∈(0,1), 都有20r
-32r
-6r
+8r
-2<0成立.情形2
r
∈[ζ
,1).此时h
(r
)≤0, 结合(17)式, 有Φ
′(r
)=g
(r
)+αh
(r
)≤g
(r
)<0.综上, 对r
∈(0,1), 恒有Φ
′(r
)<0, 从而Φ
(r
)在(0,1)上单调递减.又Φ
(0)>0且Φ
(1)<0, 所以方程Φ
(r
)=0在(0,1)内存在唯一根r
(α
).证毕.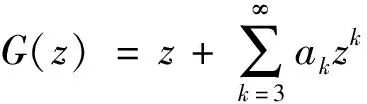
推论
若G
(z
)∈S
且G
″(0)=0, 则由(3)式定义的双调和映射W
在{z
:|z
|<r
}内是单叶且α
阶全凸的.其中r
=r
(α
)是等式(6α
-8)r
+(30-20α
)r
+(22α
-38)r
+(15-9α
)r
+(3-5α
)r
+(9α
-9)r
+3-3α
=0在(0,1)内的最小正根.
证明
类似于定理5的证明过程, 只要证T
(r
)≤3, 其中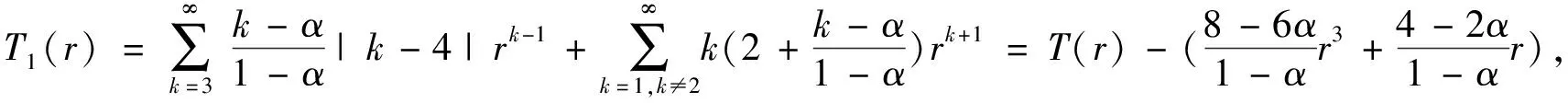
T
(r
)由(15)式给出.显然,T
(r
)≤3等价于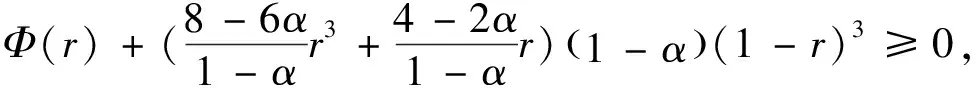
Φ
(r
)由(16)式给出.即Φ
(r
)=(6α
-8)r
+(30-20α
)r
+(22α
-38)r
+(15-9α
)r
+(3-5α
)r
+(9α
-9)r
+3-3α
≥0,当0<r
≤r
时, 有Φ
(r
)≥0, 其中r
(α
)是方程Φ
(r
)=0在(0,1)内的最小正根.得证.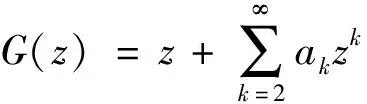
α
)r
+(8α
-16)r
-(1+α
)r
+(15-11α
)r
+(11α
-13)r
+3-3α
=0在(0,1)内的唯一根.
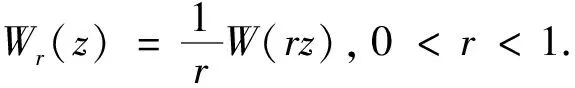
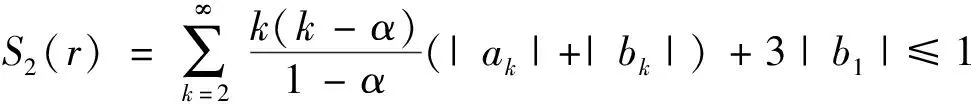
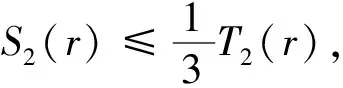
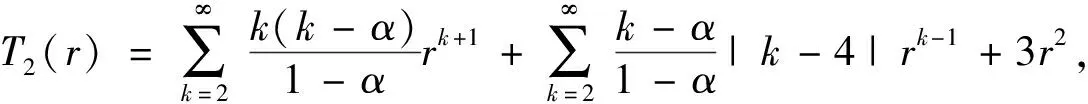
T
(r
)≤3时, 有S
(r
)≤1.计算可得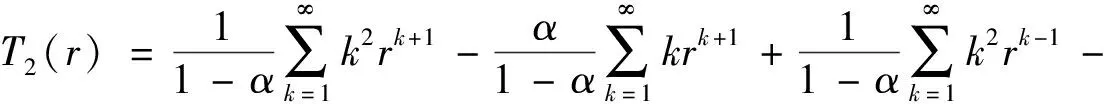
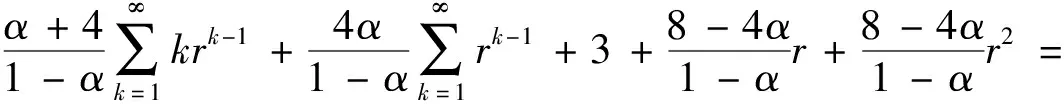
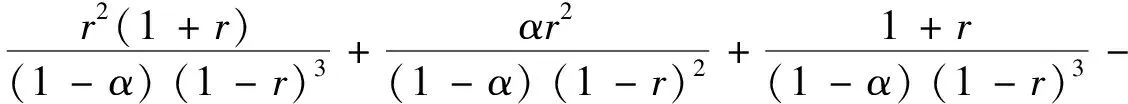
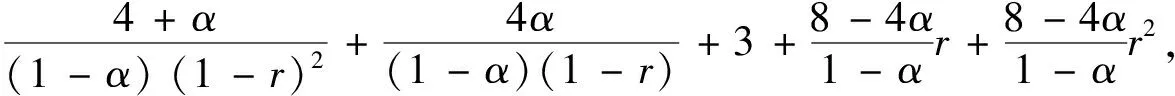
T
(r
)≤3等价于r
满足Φ
(r
)≥0,其中Φ
(r
)=(8-4α
)r
+(8α
-16)r
-(1+α
)r
+(15-11α
)r
+(11α
-13)r
+3-3α
,因为Φ
(0)=3-3α
>0且Φ
(1)<0, 所以方程Φ
(r
)=0在(0,1)内存在r
(α
), 使得当0<r
≤r
时, 有Φ
(r
)≥0, 进而有S
(r
)≤1, 从而W
(z
)在|z
|<r
内是单叶且α
阶全凸的.其中r
(α
)在(0,1)内的唯一性证明与定理5类似.
