不确定时滞耦合复杂网络的滑模追踪控制

方 娜,许丹莹,姜明浩，方 洁*

(1.郑州轻工业大学 软件学院，河南 郑州 450002；2.郑州轻工业大学 电气信息工程学院，河南 郑州 450002)

工程实际中包含着各种各样的复杂网络，如互联网、基因网络、电力系统网络和神经网络等.借助计算机强大的计算能力，使得对复杂网络的定量和定性特征进行科学分析日趋简化，且近年来对复杂网络的研究已成为中外学者的研究热点.对复杂网络的可控性和控制方法的研究是复杂网络研究的一个重要分支.如何设计简单有效的控制器，使复杂网络中的节点能够快速达到设定的轨道，实现精准跟踪外部参考信号是复杂网络控制研究的一个重要方向.目前实现复杂网络控制的主要方法有自适应控制、反馈控制、脉冲控制等.

由于信号的传输速度有限，所以在网络传输中经常会出现时滞现象，使信号传递发生在不同的时间内.时滞的类型多种多样，如内部时滞、耦合时滞和其他混合时滞等.此外，对于很多实际的复杂网络，总是不可避免地存在网络自身的不确定性以及外界干扰的影响.因此，对具有不确定参数、外界干扰和时滞的复杂网络进行控制研究更具有实际意义.梁义等引入了节点含时滞且具有耦合时滞的复杂网络同步模型, 通过设计线性控制器和自适应控制器,给出了实现同步的充分条件.方洁等研究了具有不确定参数、外界干扰及时变时滞耦合的复杂动态网络，设计了自适应鲁棒控制器，实现了复杂网络的修正函数投影同步.

在诸多混沌控制方法中，滑模控制是一种具有较强鲁棒性的控制方法，其通过控制律的切换，将系统状态从初始状态强制转移到某个预定的滑模面上，使被控系统具有对系统参数变化不敏感、抗干扰性能好和跟踪能力强等优点.对两个系统之间的滑模追踪控制已有很多相关报道，而对如何基于滑模控制方法实现复杂网络的追踪控制的研究报道相对较少.柳爽等针对一类参量未知的混沌系统构成的不确定网络，通过滑模控制器设计，实现了对未知参量的识别和对外部信号的追踪同步.张檬等基于滑模控制原理及有限时间稳定性理论,设计了滑模控制器，实现4个不确定复杂网络间的有限时间组合同步.Ghada等基于有限时间稳定性理论和自适应律，设计了一种实现有限时间滞后同步的自适应滑模控制器，实现了具有时变耦合时滞、完全未知参数和扰动无穷大的两个不确定复动力网络之间的时滞同步.Jing等通过设计周期性间歇反馈控制器，实现了两个时变时滞复杂网络的有限时滞同步.

论文在上述文献基础上，以Lorenz混沌系统作为复杂网络的节点，基于滑模控制方法，研究了具有模型不确定和外界扰动的时滞耦合复杂网络的追踪控制问题.通过设计滑模控制器，使得动态复杂网络从任意初始状态出发都能达到滑模面上并最终追踪设定的参考信号.文中外部参考信号可以任意设定为不动点、周期信号、混沌吸引子等.基于MATLAB的仿真结果验证了该控制方法的有效性.

1 问题描述

考虑如下形式的复杂网络模型

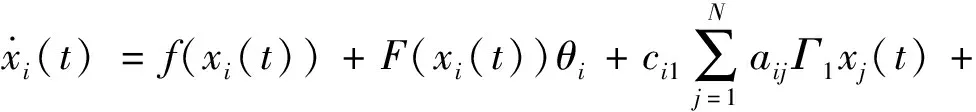
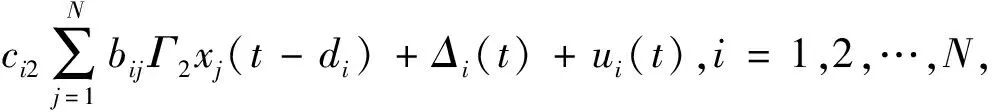
(1)

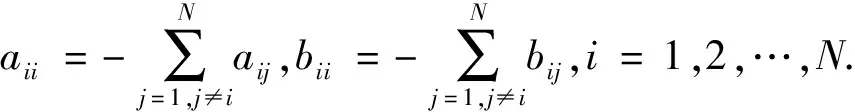
(2)

设任意给定的外部参考信号为

r

(

t

)，则复杂网络的第

i

个节点与参考信号之间的追踪误差为

e

(

t

)=

x

(

t

)-

r

(

t

),

i

=1,2,…,

N

.

(3)

由(1),(3)式可得

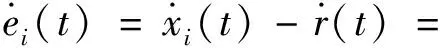
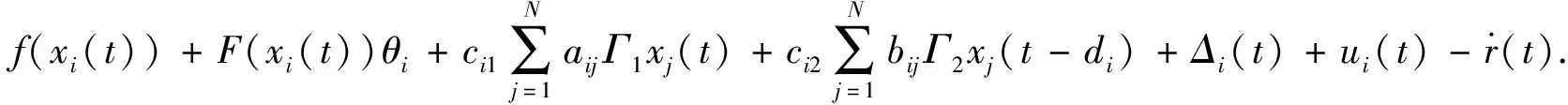
(4)

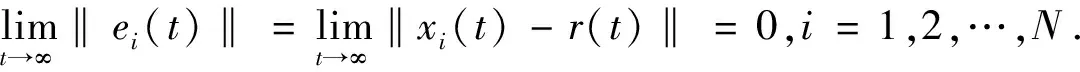
假设

外界扰动

Δ

(

t

)=[

Δ

1,

Δ

2,…,

Δ

]是有界的，即存在正常数向量

α

=[

α

1,

α

2,…,

α

],使得|

Δ

1|≤

α

1，|

Δ

2|≤

α

2，…,|

Δ

|≤

α

.

2 滑模控制器设计

设计网络节点与外部输入信号之间的滑模面如下

(5)

其中：滑模面参数

λ

,

i

=1,2,…，

N

为合适的正常量.

控制器的设计目的是为了保证追踪误差的轨迹快速进入设定的滑模面内，并始终保持在滑模面上，由此，可设计滑模追踪控制器如下

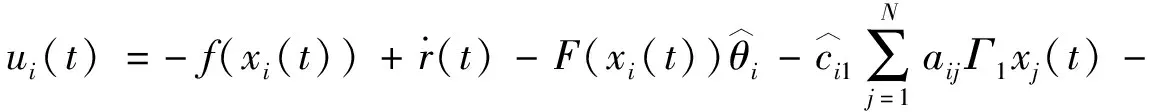
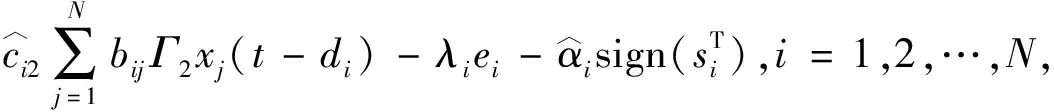
(6)

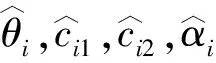
网络未知参数和耦合强度的自适应律如下

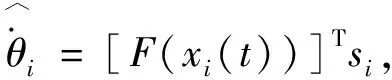
(7)

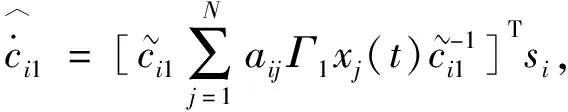
(8)

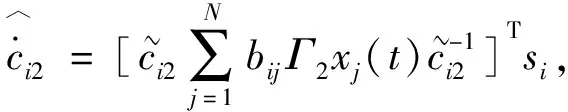
(9)

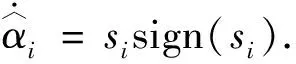
(10)

定理

对复杂网络系统(1)，在控制器(6)和自适应律(7)～(10)的作用下，复杂网络的所有节点能够追踪外部参考信号

r

(

t

).

证明

选择正定的Lyapunov泛函为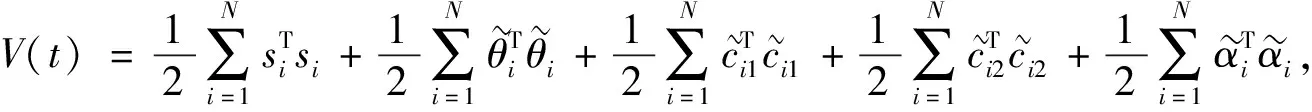

(11)

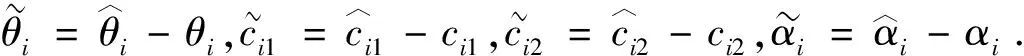
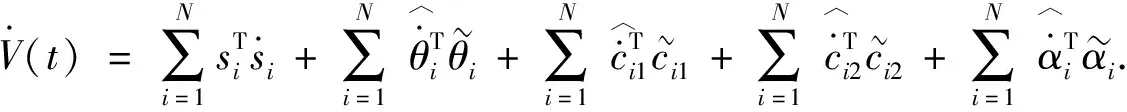
(12)

因为

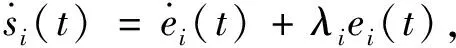
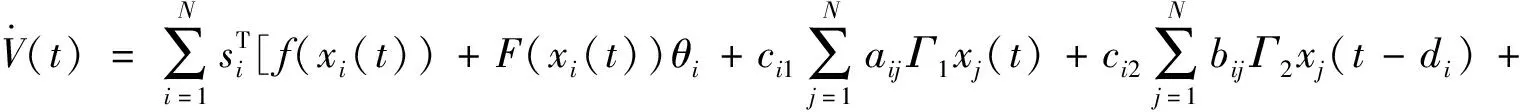
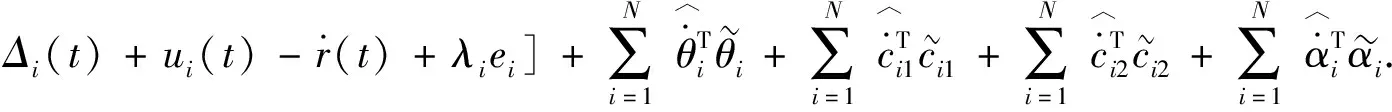
(13)

将控制器式(6)代入上式可得

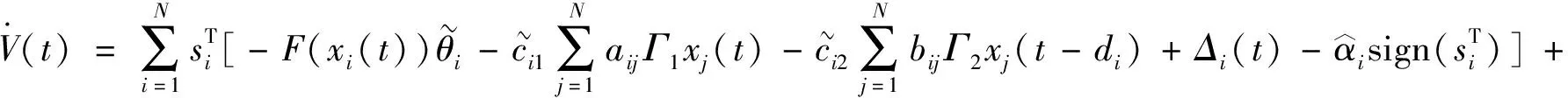
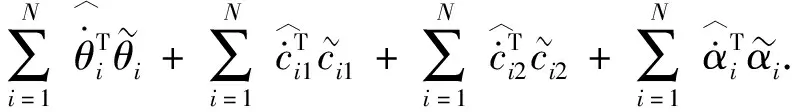
(14)

将自适应律(7)～(9)代入上式可得

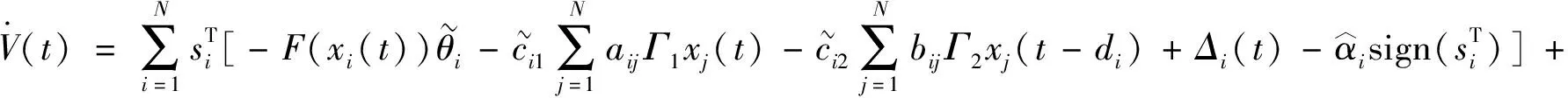
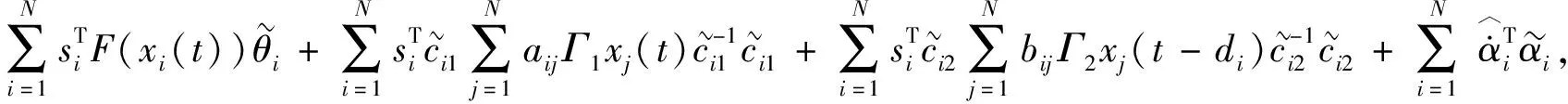
(15)

化简上式可得

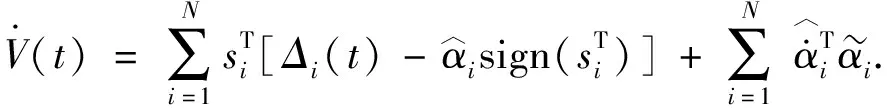
(16)

将自适应律式(10)代入上式可得

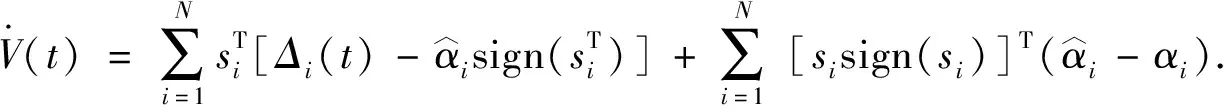
(17)

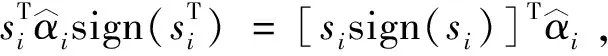
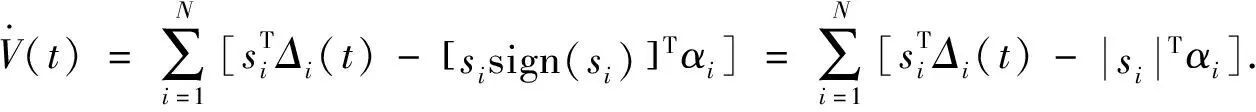
(18)

由假设中|

Δ

(

t

)|≤

α

,

i

=1,2,…，

N

可得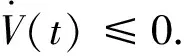

(19)

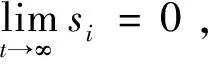
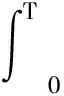
3 仿真实验

选择Lorenz混沌系统作为网络节点来验证论文方案的正确性.Lorenz混沌系统描述如下

其中：

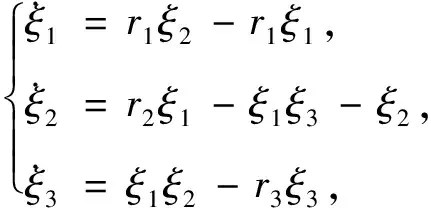
ξ

,

ξ

,

ξ

为状态变量；

r

,

r

,

r

为系统参数.当

r

=10,

r

=28,

r

=8/3时，该系统处于混沌状态.

复杂动态网络描述如下

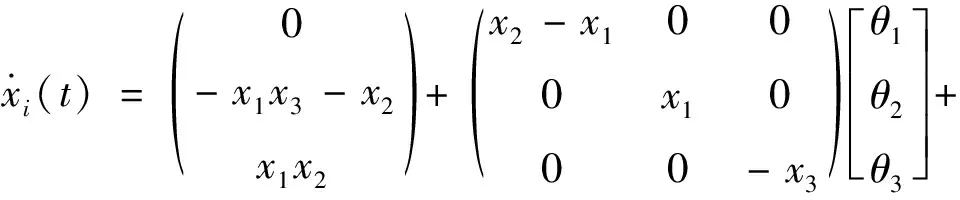
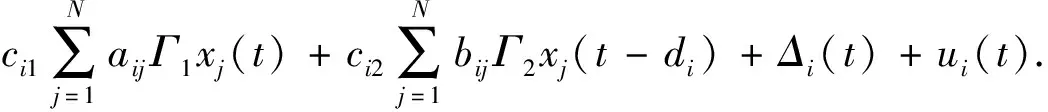
在数值仿真中，设定外耦合矩阵为

网络节点数

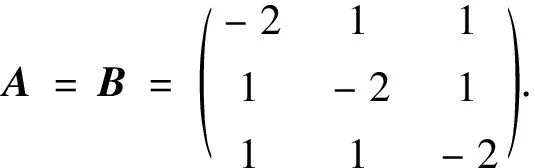
N

=3，3个节点的状态变量分别为[

x

,

x

,

x

],[

x

,

x

,

x

],[

x

,

x

,

x

].外界扰动

Δ

(

t

)=[0.3cos(

t

),0.2sin(

t

),0.5sin(

t

)],

i

=1,2,3.

c

1=

c

2=0.1，

Γ

=

Γ

=

I

，时滞

d

=

d

=

d

=1 s，外部输入参考信号

r

=sin(

t

)，滑模面常数取为

λ

=1,

λ

=3,

λ

=1.仿真结果如图1，2所示.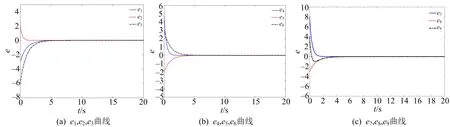

图1 误差变量ei(i=1～9)随时间变化曲线

图1中(a)～(c)分别为节点1～3与参考信号之间的误差变量

e

随时间变化曲线；图2中(a)～(c)为节点1的状态变量随时间变化曲线,(d)～(f)为节点2的状态变量随时间变化曲线，(g)～(i)为节点3的状态变量随时间变化曲线.由图1,2可知，误差信号

e

～

e

经过短时间的振荡后迅速衰减到零，网络节点1～3中的状态变量随时间演化均与外部输入信号

r

=sin(

t

)趋于一致，实现了复杂网络对外部参考信号的追踪控制.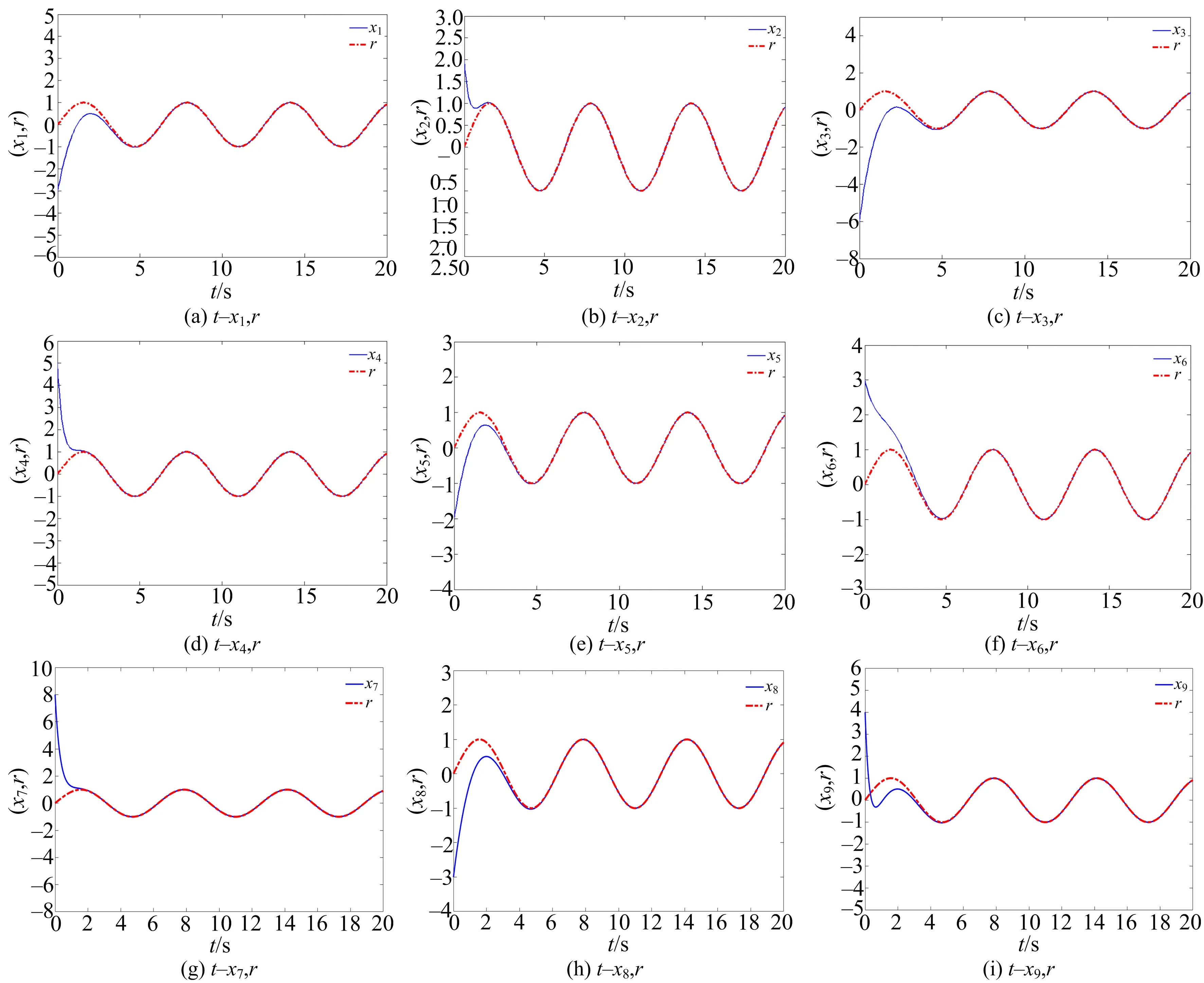

图2 状态变量随时间变化曲线

4 结束语

论文研究了不确定时滞耦合复杂网络的滑模追踪控制问题，基于滑模控制思想，设计滑模自适应控制器实现对复杂网络的追踪控制.理论分析和仿真结果表明，经过短暂的时间演化，所有网络节点中的状态变量都能实现对参考信号的追踪控制.论文的控制方法对不确定的系统模型和外界干扰具有较强的鲁棒性，为复杂网络的控制和应用提供了理论参考.