空间连续型机器人自适应鲁棒容错控制

邱小璐，蔡志勤*，刘忠振，彭海军，，吴志刚

(1.大连理工大学 工程力学系，大连 116024； 2.大连理工大学 工业装备结构分析国家重点实验室，大连 116024)

1 引 言

随着空间技术的蓬勃发展，空间机器人已经开始承担并完成一些有难度的空间任务，如空间太阳能电站的构建、航天飞船燃料的加注和空间设备的安装等。与传统空间机器人不同，空间连续型机器人具有良好的弯曲特性和较强的灵活性，能更好地在非结构、狭窄和有限的工作空间内完成航天器或星上设备的故障检测及维修等精细在轨服务任务，也可以通过自身的主动弯曲变形，完成对失效卫星的捕获和回收，这些都使其具有更广泛的应用前景和更高的研究价值，其动力学与控制问题已经成为研究热点[1-3]。

相比传统空间机器人，空间连续型机器人具有高度非线性的特点，加上空间机器人工作环境复杂，机器人自身存在参数摄动[7-9]、外部干扰[10]和测量噪声，基于力学原理的建模[4-6]往往不能完全精确描述其动态特性，给控制器的设计增加了难度。Zhao等[1]通过时延估计技术来预测模型输出，基于低精度模型实现了连续型机器人的位置控制。Chen等[10]使用RBF神经网络逼近动力学模型，采用快速终端滑模提高了控制器收敛速度。Li等[11]采用卡尔曼滤波器实现了基于无模型的控制，降低计算负荷提高控制性能。

空间机器人在长期作业的情况下，频繁的工作会导致其执行器发生故障，若是不能及时处理，会导致系统控制性能下降，甚至发生不可估计的后果。同时，空间机器人一旦执行器发生故障，缺少地面支持，极难维修。因此，提高空间机器人的容错能力使得控制系统具有较高的可靠性，也是在轨服务急需解决的问题。雷荣华等[12,13]采用神经网络分别补偿空间漂浮基机器人的模型参数摄动和估计执行器的有效因子，设计了自适应分散容错算法，两种算法均未考虑存在不确定外部扰动时控制器的鲁棒性。毕伟等[14]采用自适应律估计扰动上界，结合反步法，实现地面刚性机械臂的轨迹跟踪，但该方法未对模型参数摄动进行研究。

基于此，本文提出自适应鲁棒容错控制器解决空间连续型机械臂系统三臂节执行器并发故障时的轨迹跟踪问题。与上述研究采用神经网络或自适应律估计故障或扰动下界[13,14]不同，本文采用自适应神经网络调节滑模控制器的切换项增益，设计的滑模切换项用来抑制故障因子、模型参数摄动和外部扰动，这些都使得控制器具有较强鲁棒性的同时也满足了控制要求。

2 空间机器人动力学模型

基于等曲率假设，建立三臂节空间连续型机器人系统的动力学模型。连续型机器人几何位形为平面运动，如图1所示。αk(k=1,2,3)为第k臂节的弯曲角度，θk为Ok-XkYk相对于O-XY的转角，(xk,yk)T是Ok在O-XY的坐标。

选取系统广义坐标

q=[α1,α2,α3]T

(1)

空间连续型机器人系统动能T由节盘动能Td和柔性支撑动能Ts组成。

(2)

式中M为系统的质量阵。

连续型机器人系统弹性力Qe的虚功为

(3)

式中E为柔性支撑的弹性模量，A为其截面面积，l为其长度，ε为弯曲应变，s为力作用点到局部坐标系原点的弧长。

连续型机器人系统驱动力Qa的虚功为

(4)

与速度二次项有关的广义力Qv为

(5)

空间连续型机器人系统动力学方程为

(6)

考虑执行器故障为乘性故障，将驱动力τ=[τ1,τ2,τ3]T分离，可以得空间连续型机器人系统动力学方程

(7)

考虑模型参数摄动和外部扰动的空间连续型机器人系统动力学方程为

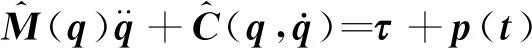
(8)

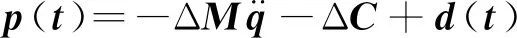
(9)

式中ΔM和ΔC为模型参数不确定项，d(t)∈R3 × 1

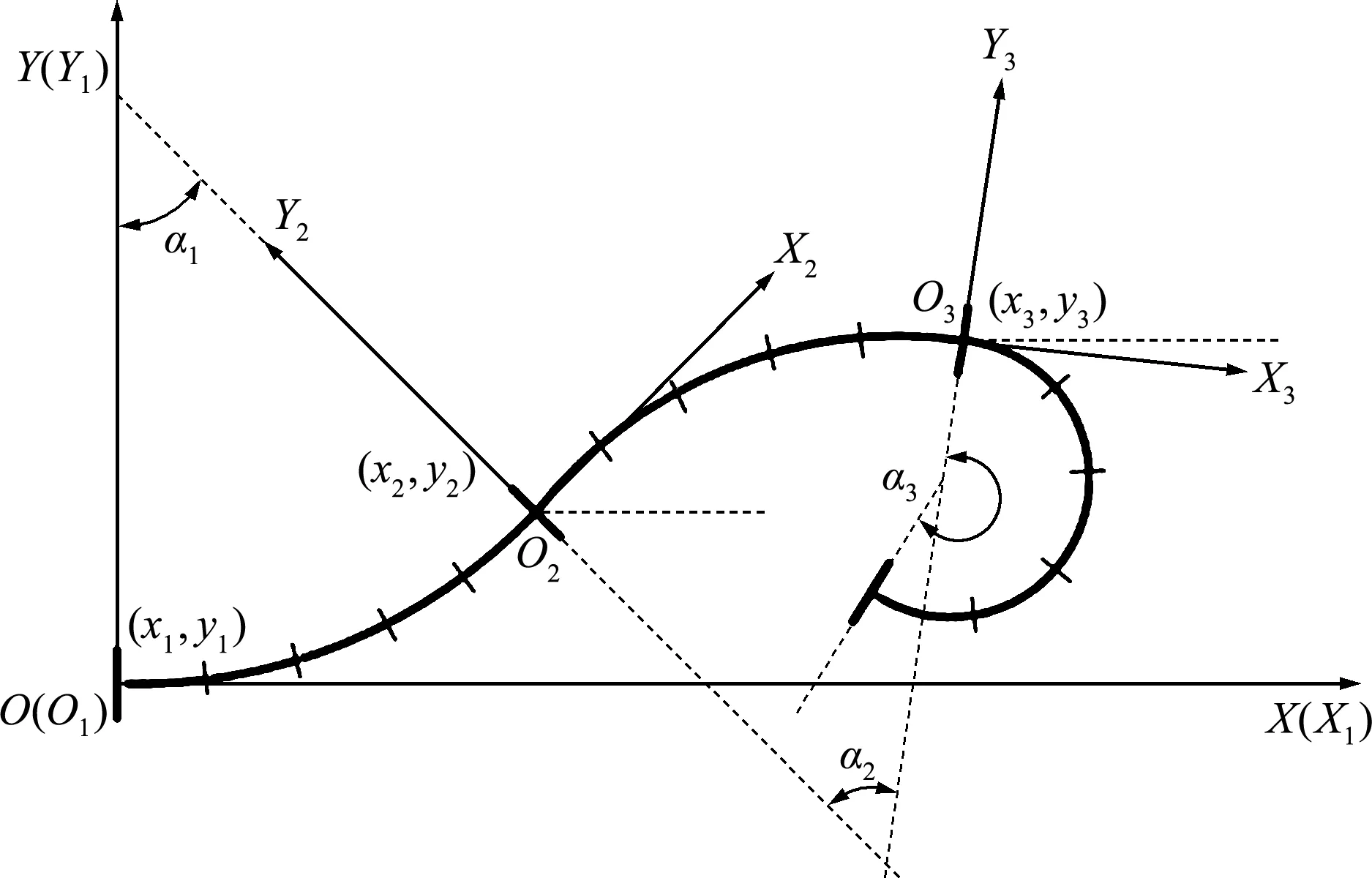
图1 连续型空间机器人系统几何位形

为外部干扰项。

3 空间机器人容错控制算法设计

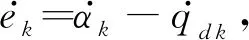
假设2p(t)有已知上界，即

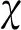
定义快速非奇异滑模面为

(10)

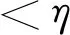
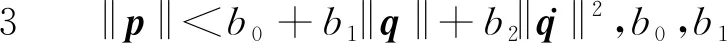
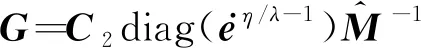
U=-[sTG]T/‖sTG‖2‖s‖‖G‖

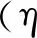
(11)

式中I3∈R3 × 3为单位阵。

为了保证闭环系统的运动在有限的时间内到达滑模面，非奇异快速终端滑模控制律如下，

τ=τ0+u0+u1

(12)

(13)

(14)

(15)

式(13，14)为等效控制律，当无模型参数摄动和外部干扰即p(t)=0时，可以单独实现对期望轨迹的跟踪控制，式(15)为切换项，p(t)≠0时，用来抵消由模型参数摄动和外部干扰引起的跟踪误差。

利用自适应RBF神经网络来估计b0,b1和b2为切换项增益，并自适应调节网络权值的更新。

三个RBF神经网络的输入和输出分别为

(16)

(17)

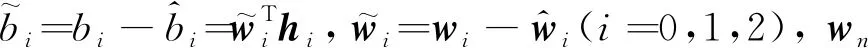
由此，基于自适应神经网络的终端滑模控制律的切换项为

(18)

4 稳定性分析

定理1 对于动力学方程(3)，控制律(7)确保位置误差在有限时间内收敛到0。

证明 结合式(8)求取误差动力学方程有

(19)

将式(13,14)代入式(19)，有

(20)

由式(14)构造

(21)

选择Lyapunov函数如下

(22)

式中Γ0，Γ1和Γ2为正定矩阵。

对式(22)求取一阶导，有

(23)

将式(13,16)代入式(23)，根据假设3有

(24)

三个网络权值自适应更新律为

(25)

5 仿真算例

对图1所示三臂节空间连续型机械臂系统，在Matlab中，采用四阶-五阶龙格-库塔求解器进行动力学求解，采样步长为0.01s(单位s)。通过三个算例验证本文算法的有效性。

机械臂物理参数选取如下，节盘质量和半径分别为md=0.01 kg，r=3.02×10-2m，柔性支撑长度和质量分别为l=0.6 m，ms=0.01 kg，弹性模量和截面惯性矩分别为E=1.67×104N·m-2，I=1.92×10-12m4。

RBF神经网络的径向基函数选取如下，

(m=1,2,…,7,i=0,1,2)(26)

式中bm为径向基函数基宽向量，cm i为中心向量，网络隐含层节点数目为7。

图2为空间连续型机器人三臂节的跟踪误差曲线。可以看出，两种算法都能在容错的同时实现轨迹跟踪控制。本文提出的控制自适应跟踪控制算法可以实现在8 s，5.5 s和4 s时，跟踪误差收敛到0，比文献[13]的控制算法收敛速度快，超调量小。5 s后，两个控制器的跟踪精度和速度都有较好的表现。

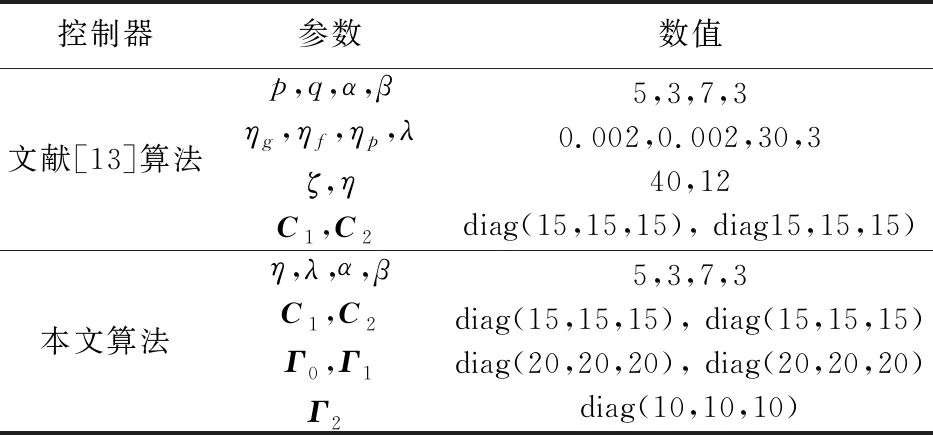
表1 控制器参数

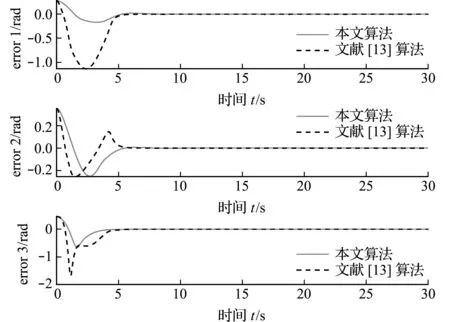
图2 无干扰下常值期望跟踪误差曲线

算例2仿真采用与算例1相同的有效因子,系统初始位置为(0.17 rad,0.17 rad,0.17 rad)，控制参数列入表2。在0 s～5 s内，对三臂节均施加常值干扰；在5 s～10 s内，对第二臂节施加干扰sin(q2)；在15 s～20 s内，对第三臂节施加干扰sin(q3)，其余时刻干扰为0。三臂节弯曲角度的期望轨迹如下,

qd 1=(π/18)sin[(π/9)t]+π/8

qd 2=(π/18)sin[(π/9)t]+π/7

qd 3=(π/18)sin[(π/9)t]+π/6

图3验证了本文算法对扰动和模型参数摄动的抑制能力。可以看出，两种算法都能完成跟踪任务。第二臂节在5 s～10 s内受到时变干扰，与文献[13]相比，本文算法的跟踪误差基本收敛。这说明本文算法对外部扰动和参数摄动具有更强的抑制能力。同时本文算法也在5 s，3 s和2 s内完成了轨迹跟踪任务，具有更快的收敛速度。

本算例采用了较小的有效因子来验证本文算法的容错能力。图4表明，当故障较严重时，在 5 s～10 s内，第二臂节受到时变干扰，文献[13]算法的跟踪误差曲线并未完全收敛，本文算法在实现跟踪误差收敛的同时，控制器具有更快的收敛速度和更小的超调量，即具有更好的动态性能，控制器保持较强的鲁棒性。

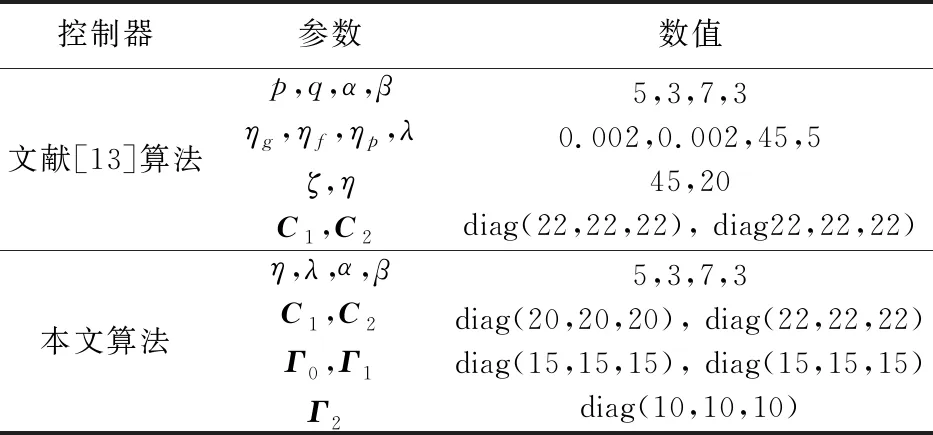
表2 控制器参数

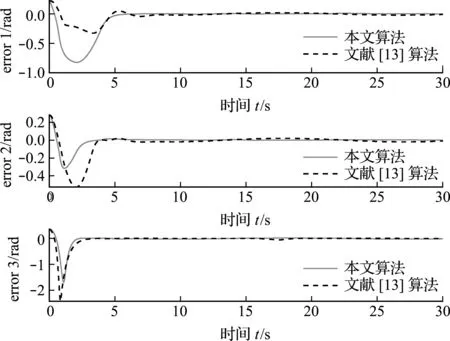
图3 干扰下时变期望跟踪误差曲线

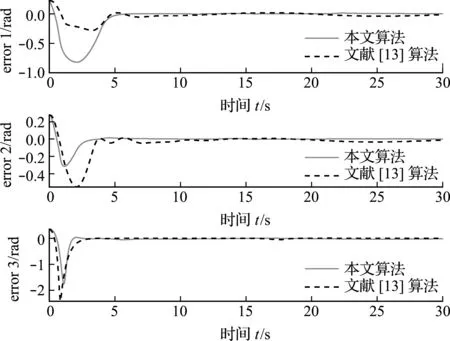
图4 干扰下时变期望跟踪误差曲线

6 结 论

针对空间连续型机器人系统三臂节执行器并发故障的情况，提出一种自适应鲁棒容错控制算法。采用快速非奇异终端滑模控制器，同时通过神经网络自适应调节控制器的切换项增益，实现空间连续型机器人的轨迹跟踪控制。

仿真验证了控制器的有效性和对模型参数摄动和外部干扰的抑制能力。结果表明，本文提出的控制器优点如下。非奇异快速终端滑模避免了计算奇异现象；本文采用自适应神经网络调节切换项增益，与文献[13]相比，对于常值型和时变型两种轨迹，本文都具有更高的跟踪精度和更快的跟踪速度；与文献[13]相比，本文所设计的切换项可以更有效地抑制模型参数摄动和外界干扰，具有更强的鲁棒性。在后续工作中，可以在此基础上解决执行器与传感器同时发生故障的容错控制问题。