夹具定位误差计算自动化方法*

朱成龙 吴玉光

(杭州电子科技大学机械工程学院，浙江 杭州 310018)

夹具是机床切削加工的重要工艺装备，定位误差是评价夹具性能的关键指标，夹具定位误差分析是夹具设计的重要任务。通常情况下，夹具定位误差分析首先需要针对具体工件的定位方案建立计算模型，然后利用各种误差计算方法求得加工表面的定位误差。由于工件几何形状千变万化，定位方案多种多样，建立计算模型，进行分析计算均需要较高的专业知识，对夹具定位误差进行分析并得出正确的定位精度数据是一件困难的工作。因此，研究定位误差计算模型的自动建立方法，使之适用于各种定位方案并能自动获得分析计算结果，实现定位误差分析的自动化，是夹具设计人员所追求的目标。

国内外学者针对定位误差分析进行了大量的研究，提出了各种定位误差计算模型和计算方法。秦国华等[1]根据运动学原理建立工件的定位误差模型，将定位误差表达为工件与夹具定位接触点位置变化的函数。吴玉光等[2]提出的连杆机构模型，将工件相对于夹具的位置关系用加工表面与工序基准，工序基准与定位基准，定位基准与定位元件等三个机构进行表示，试图通过连杆机构位置函数建立工序基准的位置与相关尺寸之间的关系。郭晓光[3]用概率方法分析夹具的定位误差，并与常用的极值法进行了比较，从而得出概率分析方法。康秀敏[4]建立了三维定位误差影响加工精度的数学模型，运用矩阵计算法与工件的定位误差进行了计算，并分析了三种典型定位方式下夹具工件的定位误差。Asante[5]提出了一种基于约束的零件-夹具装配公差分析方法，根据约束关系建立刚体的小位移旋量SDT与工件的定位误差之间的关系。Kang等[6-7]利用雅可比矩阵建立了定位点位置变动与工件位置变动的关系模型，他们的方法考虑了定位元件位置误差和定位元件形变引起的误差，从而期望能更加精确地预测加工表面的偏差。

以上研究工作为建立了各种夹具定位误差的计算模型，这些方法均需要手动建立计算模型，一些算法太过复杂，需要依赖较高的专业知识才能获得正确的结果。本文提出一个基于装配公差分析方法的夹具定位误差自动分析方法，该方法基于工件和夹具的三维实体装配模型，该模型中的全部零件的所有关联要素均标注了相应的尺寸公差和几何公差，该方法将工件和夹具的定位元件均当作是装配模型的组成零件，利用蒙特卡洛模拟方法得到定位元件和工件的概率抽样实例，再根据定位和装配关系确定加工部位相对于工件的具体位置，最后根据大量的位置抽样数据利用概率统计方法获得夹具的定位误差计算结果。

1 基于装配公差分析方法的定位误差自动计算原理

1.1 基于装配接触关系的加工部位位置计算方法

基于概率统计的定位误差分析方法首先需要对目标零件的装配位置进行自动计算，而装配位置自动计算必须根据零件之间的几何接触关系建立零件的齐次坐标变换矩阵，为此首先必须建立零件各种坐标系的确定规则以及各种坐标系之间的关联关系。

本文的工件-夹具系统的坐标体系的建立方法直接从装配公差分析方法的坐标系建立规则移植而来[8]。在装配公差自动分析方法中，装配模型中的零件坐标体系根据零件层次可分为机架坐标系、中间零件坐标系和目标零件坐标系，而在零件内部的几何要素也具有一个从基础基准坐标系、中间要素坐标系和目标要素坐标系的层次。装配模型中的中间零件既对它的上层零件进行定位，同时它自身又需要由下层零件来定位，因而装配模型从机架零件到目标零件形成了一个零件层次的位置和误差传递关系图。在零件内部从基础基准到目标要素也构成了一个几何要素层次上的位置和误差传递关系图，因此装配体的坐标体系包括零件之间的坐标体系和零件内部几何要素之间的坐标体系。为了使装配误差分析方法适用于定位误差求解并简化陈述，将机器装配模型的坐标体系简化成图1所示。图1a为2个零件的装配模型，2个零件分别对应装配模型的机架零件和目标零件，机架零件全局坐标系为机器坐标系Ω1，目标零件坐标系为Ω2。图1a中的其余坐标系分别为机架零件上的定位基准坐标系Ω3、目标零件上的装配基准坐标系Ω4以及目标要素坐标系Ω5。图1a中2个零件之间存在3个接触表面，由于零件存在几何误差，零件的装配接触表面由存在位置和方向误差的替代几何表示，3个接触表面根据装配顺序不同具有不同的接触状态。图1b为一工件-夹具装配模型，与一般机器装配模型相对应，工件-夹具的装配模型中的夹具坐标系φ1就相当于机器模型中的机架坐标系Ω1，在不考虑机床的误差的前提下，夹具坐标系与机床坐标系两者相对位置固定不变，因此可以假设两者统一。而工件坐标系φ2就是目标零件坐标系Ω2，加工部位坐标系φ5就是目标要素坐标系Ω5。

根据坐标变换关系，机器装配模型中零件目标要素在机器中位置的计算公式为：

pm=pw×M1×M2×M3

(1)

式中：pw=(x,y,z,1)，pw为目标要素上点在目标要素坐标系中的位置，M1为目标要素坐标系相对于工件全局坐标系的齐次坐标变换矩阵，M2为目标零件全局坐标系相对于机架零件第一定位基准坐标系的齐次坐标变换矩阵，M3为机架零件第一定位基准坐标系相对于机架零件全局坐标系(机器坐标系)的齐次变换矩阵，由式(1)可知，pm为目标要素上的同一点在机器坐标系的位置。M1和M3取决于零件内部的误差传递关系，而M2则取决于零件所在的装配基准和装配顺序。

夹具定位误差分析与装配体位置误差分析不同，夹具定位误差分析目标是加工部位相对于工件坐标系的位置变动情况。在工件-夹具系统中，工件加工部位的位置取决于机床的刀具运动轨迹，在不考虑机床和刀具轨迹等误差的前提下，可以认为工件加工部位相对于夹具坐标系的位置是不变的。也就是说，对于一般的机器装配模型，式(1)中的pw的位置以及变动范围取决于公差指标，pm可以通过公式计算得到。对不同的零件pm是变化的，而在工件-夹具系统中，pm却是不变的，而工件坐标系相对于夹具坐标系的位置是变化的，因此pw相对于工件坐标系是变化的，pw的变动范围就是夹具的定位误差。

在夹具-工件装配模型中，pm可以根据装配关系和理想几何计算出来，也可以通过CAD的API函数从公称实体模型中直接读出。工件坐标系由工件的基础基准决定，取决于工件基础基准之间的几何类型和位置关系。工件坐标系相对于夹具坐标系的位置取决于工件定位基准与夹具定位元件之间的接触表面类型和位置关系。由于工件定位基准存在尺寸和几何误差，使得每个工件坐标系相对于夹具坐标系的位置是变化的，从而使得每一个工件加工部位相对于工件坐标系的位置pw是不同的。pw的计算公式可以根据式(1)得出：

(2)

式(2)是工件加工部位上一个点的位置计算公式。利用式(2)，结合加工部位的几何形状就能计算出整个加工部位的位置。利用蒙特卡洛模拟方法模拟生成出一定数量的工件概率抽样实例，从而获得加工部位位置的大量概率抽样数据，然后利用概率分析方法就可以得出整个加工部位定位误差的概率统计数据。

1.2 坐标系建立规则

由于采用坐标变换矩阵计算零件定位误差、实现计算过程自动化，因此坐标系的建立规则十分重要。一般来说，零件的坐标系统必须根据设计模型或图纸要求的设置，零件的全局坐标系由零件的基础基准要素来体现，基础基准是零件模型或者图纸上的尺寸标注系统的参照基准。而工件的坐标系统由工艺基准确定，由于制造和测量工艺需要，零件的设计基准有可能和定位基准、测量基准不一致，因而造成工件的坐标系统和零件的坐标系统不一致，但本文不讨论这一问题，即假设零件的设计基准和工艺基准相同，可以根据工件-夹具系统的定位关系来确定工件的坐标系统。根据工件加工部位的功能要求，工件在夹具上的定位既可能完全定位也可能存在欠定位，正定位情况下工件坐标系统可以由定位基准几何类型和定位顺序完全确定，而欠定位情况下的需要制定规则进行确定。理论上讲，任何几何要素均可以作为基准要素，但生产实际中通常只考虑平面、内外圆柱面作为工件的定位基准面的情况。 根据以上说明，本文只考虑平面、内外圆柱面作为工件的定位基准面，对常见定位方式下的正定位和欠定位情况，建立工件坐标系的确定规则，表1归纳了这些情况下的坐标系确定规则。其中，规定OF-XFYFZF为夹具坐标系，Ow-XwYwZw为工件坐标系。

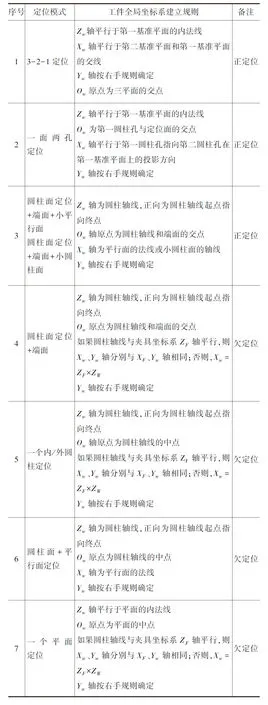
表1 工件坐标系的确定规则

2 夹具定位元件的处理

2.1 复合定位元件

在一般的机器装配模型中，对一个零件进行定位的零件数量最多不超过3个，而在工件-夹具装配系统中，工件的一个定位基准面往往就有可能与多个定位元件接触，每一个定位元件在机器装配实体模型中都属于一个单独的零件，因此会造成一个工件的定位零件数量超过3个这种情况，这就使得利用一般机器装配模型自动计算工件装配位置的公式变得十分复杂。为了便于利用齐次坐标变换矩阵计算工件在夹具上的位置，本文将与工件的同一个定位基准表面接触的多个定位元件进行组合，组合之后的定位元件作为一个特殊的定位元件处理，从而形成一类复合定位元件。复合定位元件的接触表面由组成成员的接触表面共同决定，接触表面的几何参数也由组成成员的接触表面参数确定，复合元件直接装配在夹具体的定位基准面上，复合元件的位置及其变动也相对于夹具坐标系确定。根据与工件的一个定位基准面接触的全部定位元件合成一个复合定位元件这一条件，归纳出如表2所示的复合定位元件种类。CAD装配模型包含了零件的装配接触信息，根据与工件同一定位面接触的定位元件的几何类型、相对位置就可以确定复合定位元件的类型和位置参数，从而使得定位元件的处理能通过程序自动进行。

复合定位元件的优点是可以减少定位元件的几何参数数量，并且对不同性质的参数分别进行处理。例如，定位元件的位置和定位元件的高度对工件定位精度的影响是不同的，在简化计算时就可以忽略定位元件在夹具体上的位置变化，而只需考虑定位元件的高度变化。复合定位元件作为单一的零件装配在夹具体上，对工件进行定位。经过处理之后，工件与夹具的装配问题就分解成工件和定位元件装配，然后定位元件再和夹具体进行装配，而定位原件则包括复合定位原件和常规定位元件两大类。这样工件-夹具的装配系统与机器模型的装配系统完全一致，即可以利用一般机器的装配模型求解定位原件在夹具体中的位置。

表2 复合定位元件的几何参数

2.2 实际定位元件和工件的变动仿真

定位元件与工件都是机械零件，因此都需要通过概率抽样得到零件实例。本文利用控制点变动模型[9]来抽样生成零件几何要素的实际位置和尺寸。控制点变动模型将零件上需要仿真的几何要素用具有规则边界的替代几何来表示，通过控制替代几何的顶点位置来生成几何要素的实例，而顶点位置则需要根据该几何要素的公差指标以及它的误差变动规律利用蒙特卡洛模拟方法生成。如平面要素用矩形边界的平面作为替代几何来表示其公称表面，根据平面要素的变动规律来抽样得到4个顶点的位置，从而模拟平面要素的位置变动情况。

本文假设工件定位基准，夹具体以及夹具定位元件的尺寸和位置变动均遵循正态分布规律，具体概率抽样过程说明如下。假设零件某一平面要素的位置公差值为t，即假设表示该平面要素的替代矩形的3个顶点在-t/2～t/2的区间内呈正态分布规律，即顶点位置的正态分布函数如式(3)所示。

(3)

式中：x为顶点位置参数，σ为位置参数变动的均方差，其值为t/6，μ为顶点参数的平均值，可以设置其为0。概率抽样的具体过程[10]为：首先利用随机数函数生成均匀分布的、范围在[-t/2，t/2]下的自变量x的值和范围在[f(x-μ)，f(t/2)]下函数值p，然后根据f(x)与p的关系，确定x的取舍，这里取f(x) ≥p时x的值。在得到替代矩形上任意三个顶点的位置之后，第4个顶点则可以根据平面条件利用前3个顶点的位置计算出来。

3 定位误差自动化分析软件及其实例验证

3.1 原型软件介绍

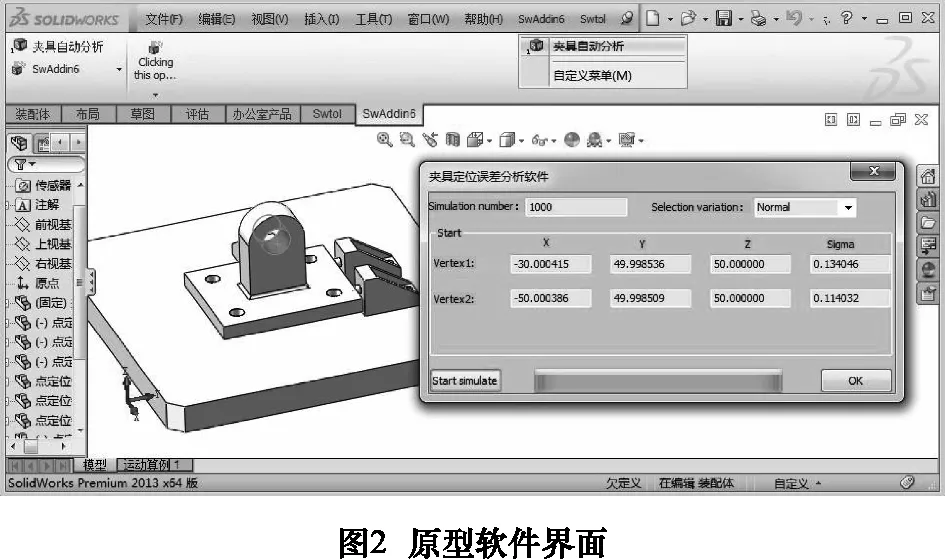
原型软件基于SolidWorks的二次开发API函数和VC++开发，该软件由误差传递关系图建立模块、公差处理模块、定位元件处理模块，控制点仿真模块、装配位置计算模块和结果处理模块组成。误差传递关系图模块首先根据零件装配关系建立零件之间的误差传递关系图，然后根据零件的装配基准到定位基准或者目标要素之间的几何要素公差关系建立零件内几何要素之间的误差传递关系图。公差处理模块根据几何要素的尺寸公差和几何公差生成几何要素公差域以及公差变量之间的关系。定位元件处理模块生成与同一个定位基准接触的复合定位元件。控制点仿真模块根据几何要素的几何类型和公差域信息建立控制点变动模型，再根据公差变动规律生成替代几何的实例。装配位置计算模块根据零件装配顺序和装配接触关系计算零件其次坐标变换矩阵的元素数值。结果处理模块根据工件加工部位的几何形状建立输出结果的数据格式，当前的版本只输出几何要素的控制点的变动结果，下一步要用常规的误差表达形式进行表示。软件的输入为工件-夹具装配模型，装配模型中所有零件实体模型均标注尺寸公差和几何公差，并且要求公差标注的格式正确。图2为原型软件的使用界面。

3.2 实例验证

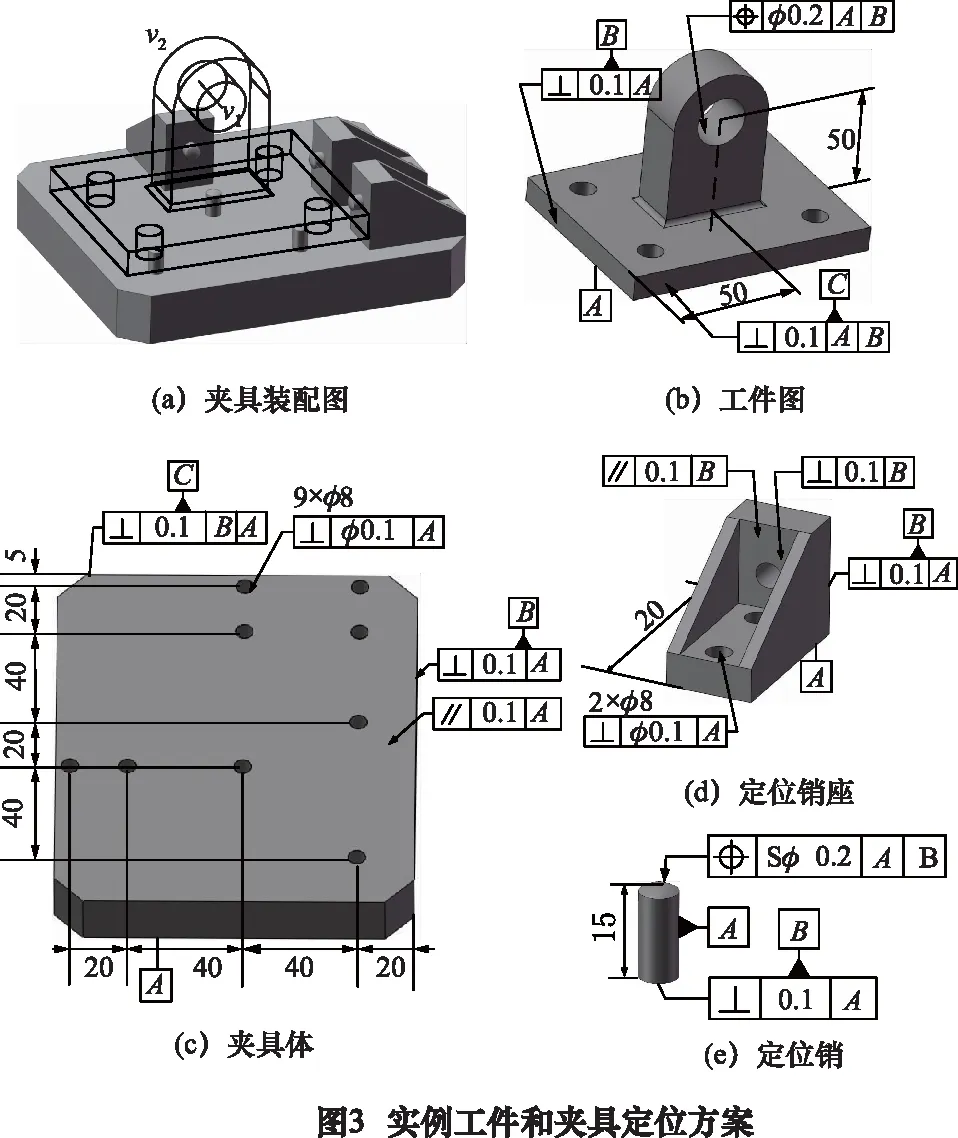
实例工件来自文献[4]，其几何形状如图3所示，实例的公差数值根据需要是本文添加的。这是一个轴承座，加工表面为轴承孔，加工精度要求为轴承孔相对于底面和侧面的位置度公差。该轴承座的夹具定位方案采用3-2-1定位，如图3所示，夹具体由1个平板和3个侧定位销组成，平板上安装3个圆柱销，另外3个侧定位圆柱销分别安装在3个侧定位支撑件上，3个底面定位销的高度公差为0.2 mm，定位销的位置度公差均为0.1 mm，这些公差数值均标在零件的实体模型上。

为了进行夹具定位误差分析，首先需要将工件-夹具的三维装配模型装入，再调用自动计算程序，然后根据程序要求选择要加工的表面，输入仿真次数。程序根据加工部位的结构自动决定输出结果的格式，对于当前实例，加工部位为一个圆柱，程序只输出圆柱轴线2个端点的坐标值变动情况，分析结果如图4所示。其中Vertex1为圆柱轴线的起点v1点的x、y、z坐标平均值，Vertex2为圆柱轴线终点v2的平均坐标值，两个sigma值分别为两端点v1和v2在偏离理想轴线位置的变动的标准差。

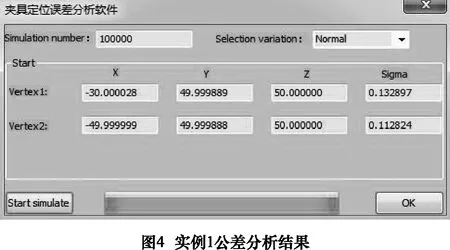
图4的结果为仿真次数10 000次情况下取得的，通过改变仿真次数可以说明仿真次数的改变对计算结果的影响并不明显，表3为不同仿真次数下的端点坐标值变动情况。

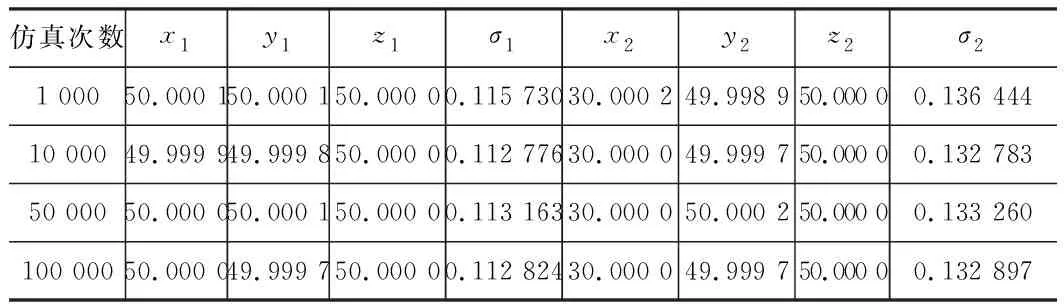
表3 仿真次数对计算结果的影响

根据文献[4]给出的计算方法，笔者用手工对该定位方案的定位误差进行了计算，轴承孔轴线两端的坐标值变动结果为x1=50±0.58 mm，y1=50±1.14 mm，z1=50±0.95 mm，x2=50±0.58 mm，y2=50±0.94 mm，z2=50±0.85 mm。文献[4]采用三维定位误差的矩阵计算法分别考虑了工件在3个坐标轴方向的位移及转动误差，而本文采用控制点变动模型生成零件实例，并没有考虑加工孔两端点在其轴线方向上的变动，所以本文方法计算的两端点v1、v2的z轴方向上的变动误差为零。

4 结语

本文提出一种夹具定位误差自动计算方法，该方法以工件-夹具系统的三维装配模型为输入，自动提取工件和夹具的公差信息，利用蒙特卡洛模拟方法生成工件和夹具概率抽样实例，根据工件夹具装配关系计算加工部位在工件上的位置，再利用概率统计方法，计算夹具定位误差的概率统计结果。利用该方法在CAD软件SolidWorks上开发了原型程序，该程序适用于常见的定位基准几何类型、定位基准的各种组合形式和常见的加工部位几何形状。经过几个简单实例的验证，定位误差结果符合实际情况，说明本文的方法能够自动进行夹具定位误差计算。本文的方法不要求用户进行大量的人机交互，也不需要使用者具有专门的夹具定位误差计算知识，因此具有较好的应用价值。下一步将考虑更加一般化的定位基准和定位方案，并且增加对机床和刀具的误差的考虑，研制更加通用化的计算程序。