冻融循环下饱和含黏粒粉砂动力学参数试验
崔高航,朱成浩
(东北林业大学 土木工程学院,哈尔滨 150040)
1 研究背景
冻融循环作用会严重影响地基土的结构性,使土的力学特性发生不可逆转的变化[1]。中国寒区的冻融循环作用十分严重,使公路、铁路等地基土的动力特性发生改变,对交通车辆的运营和设备的平稳运行构成威胁。土的动力特性改变主要体现为动剪切模量和阻尼比的变化,它们受土的结构类型、荷载性质等因素的影响,故冻融循环作用间接影响土的动力特性。
目前,对季冻区冻结土的动力特性研究较详细,但对反复冻融的含黏粒粉砂土的动力特性研究较少。Zhang等[2]对不同粗粒含量的冻结粉砂土进行循环三轴试验,发现颗粒含量对粉砂土的动力特性有很大影响。董正方等[3]对黄泛区粉砂土进行动三轴试验,提出了拟合度较高的修正Ramberg-Osgood动本构模型。常丹等[4]对青藏粉砂土进行了静三轴剪切试验,发现围压与冻融循环、冻结温度与冻融循环之间的交互作用对粉砂土的静力学性质影响均比较显著。严晗等[5]发现冻融循环对粉砂土的动剪切模量和阻尼比的影响均较大,但未进行定量分析。崔广芹等[6]通过冻融试验和土力学试验研究发现,冻融次数的增加使粉砂土黏聚力和抗剪强度先减小后增大,而对内摩擦角的影响较小。张向东等[7]对不同冻融次数的风积砂土施加动荷载,得出冻融次数的增加会使土体动弹性模量减小、阻尼比增大。以上学者主要对粉砂土的冻、融状态的力学参数进行了研究,对寒区实际环境中广泛分布的含黏粒粉砂土这种复杂混合土壤在经历冻融循环后的动力研究还较少。
本文采用松花江漫滩土体,为第四纪冲、淤作用形成的粉质黏土与粉砂土的混合物,具有粉砂的主要性质和一部分黏土的特性,有着特殊的区域特征。在此修建除住宅建筑外,还有若干跨松花江公路、公铁两用桥梁。中国寒区的轨道交通发展迅速,但有关寒区土的动力学研究还不够充分,研究该地区土体的动力特性对未来寒区的动力工程的设计与建设具有很大的参考价值。
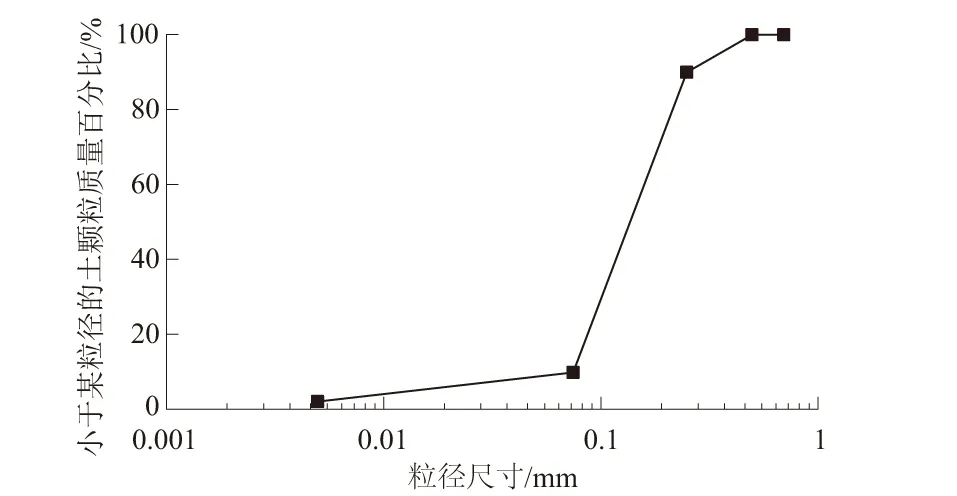
图1 粒径分布曲线Fig.1 Curve of particle size distribution
2 试验测试
2.1 土样参数
土样取自哈尔滨市松花江漫滩,通过筛分法和密度计法确定其颗粒级配,粒径分布如图1所示。根据《岩土工程勘察规范》(GB 50021—2001)[8],该土样归类为粉砂。根据《公路土工试验规程》(JTG E40—2007)[9]确定了土壤的物理参数,如表1所示。试样采用击实法制备,风干土样先用0.25 mm土工标准筛筛分,然后与蒸馏水混合均匀,初始含水率控制在15.1%。分三层击实制成直径39.1 mm、高度80 mm的圆柱试样,参照《铁路路基设计规范》(TB 10001—2016)[10]设定压实度为95%。

表1 土壤的物理参数Table 1 Physical parameters of soil
2.2 试验仪器
动三轴试验仪器为英国GDS公司生产的动态三轴试验系统,如图2所示。仪器可施加的循环荷载最大为10 kN,荷载频率范围为1~5 Hz,最大围压200 MPa。冻融循环过程采用DP.CDR-2型快速冻融试验设备,仪器及冻融后的试样如图3所示。快速冻融试验设备的温度设定范围为-17~+8 ℃。

图2 动态三轴试验系统Fig.2 Dynamic triaxial test system

图3 DP.CDR-2型快速冻融试验设备及冻融试样Fig.3 DP.CDR-2 quick freezing and thawing testequipment
2.3 试验方案
为研究冻融循环对含黏粒粉砂的动力特性影响,设置冻融0、1、3、6、10、14次。参考哈尔滨市冬季土温测试研究报道[11],选取冻结温度为-16 ℃。研究其他影响因素时采用未冻融土样,试验荷载参数参考城市轨道交通引起的环境振动[12],结合试验仪器,选取荷载频率为1、3、5 Hz,动应力幅值为40、60、80 kPa[13]。
由于在交通荷载作用时间内动应力幅值是恒定的,对粉砂土试样进行应力控制固结不排水动三轴试验。将需进行冻融循环的试样用三瓣膜、不透水板和保鲜膜密封,放置于快速冻融试验设备中,设置冻结温度并冻结6 h,然后以23 ℃融化6 h,这样完成了一次冻融循环,并编号记录。试样在三轴仪上进行CO2排气、水头差饱和、多级反压饱和,当孔隙水压力系数B值>0.95时认为完全饱和。然后将试样在有效围压下进行等压固结,固结结束标志为反压控制器中无气水的体积恒定。由于试样在1 600次循环荷载后开始液化破坏,试验施加1 500次循环荷载。试验方案如表2所示,以试样S-1为基准对照。
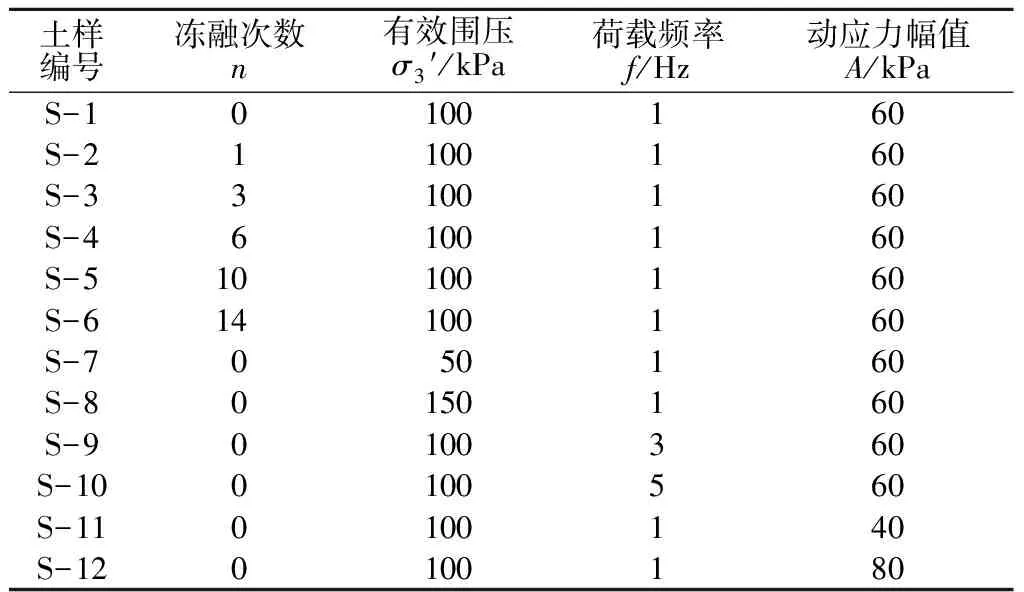
表2 试验方案Table 2 Test plans
2.4 剪切模量与阻尼比的计算
通过动三轴试验仪器采集到轴向应力σd与轴向应变εd数据,由此可以计算得到每一次循环的动剪应力τd与动剪应变γd,即
τd=σd/2 ,
(1)
γd=εd(1+μ) 。
(2)
式中:μ为动泊松比,对于饱和土μ=0.5。
每一次循环荷载作用下,动剪应力与动剪应变形成一个滞回圈[14]。将滞回圈平均斜率定义为动剪切模量Gd,即
(3)
式中:τd,max、γd,max分别为滞回圈的顶点坐标,代表最大剪应力与最大剪应变,τd,min、γd,min分别为滞回圈的底点坐标,代表最小剪应力与最小剪应变。
滞回圈围成的面积反映了塑性变形耗能的大小[15],阻尼比D的计算式为
D=Aloop/(4π·Atriangle) 。
(4)
式中:Aloop为滞回圈的面积;Atriangle为滞回圈顶点与原点、剪应变轴围成的三角形面积。
3 试验结果
3.1 动应力幅值的影响
在100 kPa有效围压、1 Hz荷载频率条件下,未冻融粉砂土的动剪切模量在不同动应力幅值下的变化如图4(a)所示。剪应变较小时,动剪切模量减小比较缓慢,在某一剪应变水平发生转折,然后迅速线性减小。Lin等[16]认为转折点动剪切模量可以评价动应力幅值的影响。图4(a)中动应力幅值A为40、60、80 kPa时,转折点动剪切模量分别为20.83、17.39、11.08 MPa,因此在40~80 kPa动应力幅值范围内,转折点动剪切模量随动应力幅值的增加而减小。
在100 kPa有效围压、1 Hz荷载频率条件下,未冻融粉砂土的阻尼比在不同动应力幅值下的变化如图4(b)所示。阻尼比随剪应变的增加而增大。为了方便研究,认为最小剪应变时对应的阻尼比为最小阻尼比,用该值来评价动应力幅值的影响。对比发现,幅值60、80 kPa时的最小阻尼比相较幅值40 kPa时分别增加0.03、0.07,即幅值越大,最小阻尼比越大。
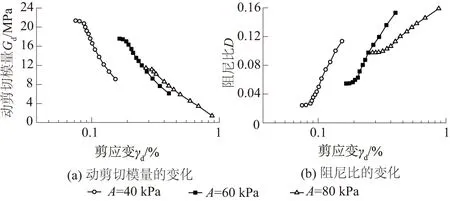
图4 不同动应力幅值下Gd与D的变化Fig.4 Changes of dynamic shear modulus Gd anddamping ratio D under different dynamic stressamplitudes
3.2 冻融循环的影响
3.2.1 试验数据
土样在60 kPa动应力幅值、100 kPa有效围压、1 Hz荷载频率条件下,经历0、1、3、6、10、14次冻融循环后动剪切模量的变化如图5(a)所示。第1次冻融后,转折点动剪切模量下降5.24 MPa。第3、6、10次冻融后,转折点动剪切模量增大,逐渐接近未冻融时的数值,这与纯黏土、砂土冻融循环下动剪切模量变化规律有所不同[17]。第14次冻融后,转折点动剪切模量大幅下降,不再随冻融次数的增加而增大。
为研究阻尼比的变化速度规律,以最小阻尼比为基础值进行归一化处理。不同冻融次数下归一化阻尼比的变化如图5(b)所示。未冻融时,阻尼比随剪应变变化的曲线斜率很大,接近线性;冻融1次时,曲线斜率大幅减小;随着冻融次数的增加,曲线斜率逐渐增大,呈“上凸肚”型;冻融10次时,曲线斜率逼近未冻融时的斜率;冻融14次时,曲线斜率再次大幅减小,呈“下凸肚”型。结果表明,该含黏粒粉砂土对冻融循环非常敏感,冻融次数与动剪切模量、阻尼比的变化关系并不是单一的趋势。
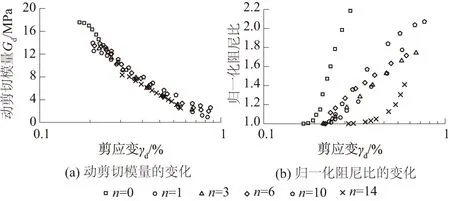
图5 不同冻融次数下Gd与D的变化Fig.5 Changes of Gd and D undergone differentfreeze-thaw cycles
3.2.2 内在机理
动剪切模量受冻融循环影响的复杂性表现在:不同冻融次数区间内,动剪切模量的发展趋势是不同的。土样在60 kPa动应力幅值、100 kPa有效围压、1 Hz荷载频率条件下,以转折点的动剪切模量为评价标准,作出转折点动剪切模量与冻融次数的变化图,如图6所示。
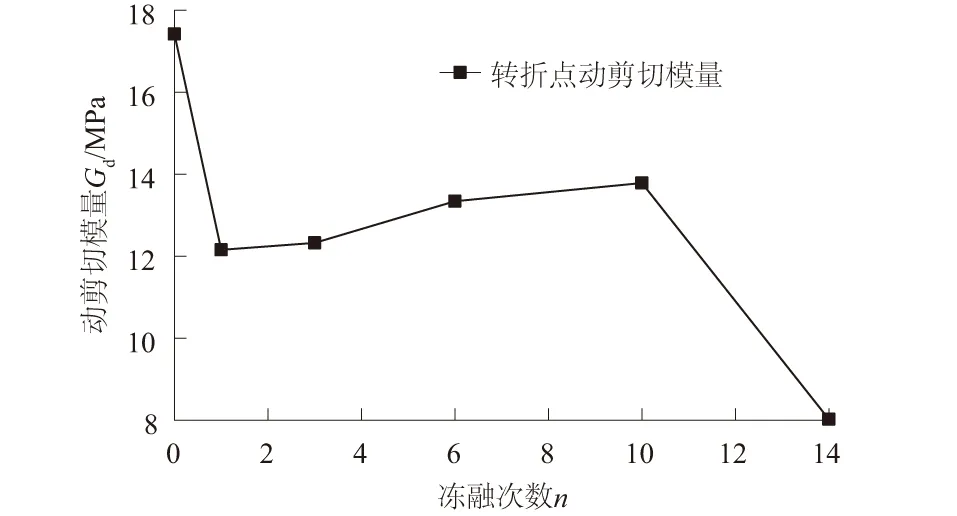
图6 转折点的Gd随冻融次数的变化Fig.6 Change of Gd at turning point with freeze-thawcycles
冻融1次后,转折点动剪切模量大幅下降。在冻结时,液态水转变成固态冰,体积增加9%,原本紧密连结的土颗粒被冰推开,形成微小裂隙[18]。融化后,土中裂隙仍然存在,土结构相较冻融前疏松,因此动剪切模量下降。在封闭体系的冻融循环下,没有外界水分的补充,水冻结后的体积膨胀对土体结构的影响是有限的。冻融过程中,土中的颗粒组成、孔隙分布逐渐调整,随冻融次数增加而趋于稳定,转折点动剪切模量有所回升。
从第1次冻融开始,土体内的楔形力不断发展。当冻融次数较少时,楔形力较弱,应力累积还不足以抵抗黏粒的黏结力,此时黏土颗粒冻融特性占主导,动剪切模量随冻融过程增加。当冻融14次时,楔形力占据主导地位,土体结构开始破坏,动剪切模量停止回升,转折点动剪切模量比冻融1次时下降34%。
3.3 围压的影响
在60 kPa动应力幅值、1 Hz荷载频率条件下,未冻融粉砂土在不同有效围压下动剪切模量的变化如图7(a)所示。以转折点的动剪切模量为评价标准,当有效围压增大时,动剪切模量增大。有效围压从50 kPa增加到150 kPa,转折点动剪切模量增加了653%。这是因为随着有效围压的增大,土样内部的间隙逐渐消散,土颗粒间贴合得越紧密,土的骨架可以承受更大的剪应力,动剪切模量更大。
未冻融粉砂土在不同有效围压下阻尼比的变化如图7(b)所示。随着有效围压增大,最小阻尼比减小,且有效围压为100、150 kPa时,随着剪应变的增大,阻尼比增加速度变缓。
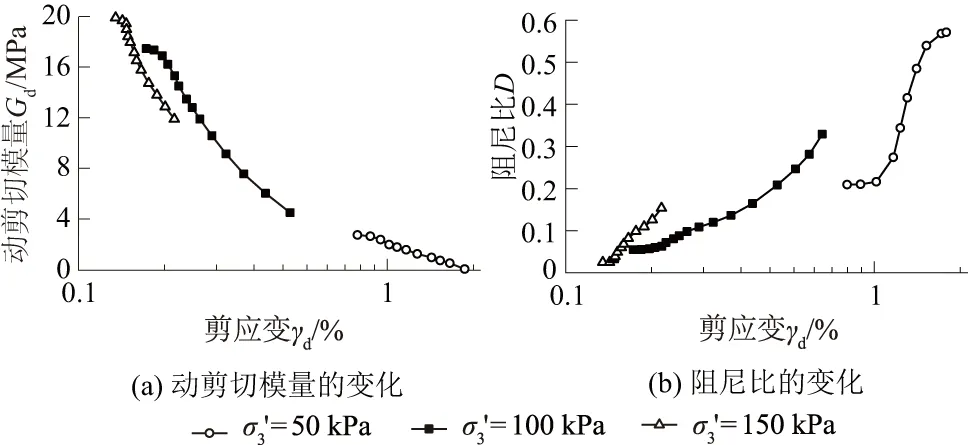
图7 不同有效围压下Gd与D的变化Fig.7 Changes of Gd and D under different effectiveconfining pressures
3.4 频率的影响
在60 kPa动应力幅值、100 kPa有效围压条件下,未冻融粉砂土在加载频率为1、3、5 Hz时,动剪切模量和阻尼比的变化如图8所示。当加载频率从1 Hz增加到3 Hz,转折点动剪切模量增加0.4%,最小阻尼比减小68.7%;当加载频率从1 Hz增加到5 Hz,转折点动剪切模量增加26.0%,最小阻尼比减小90.0%。可见,随着加载频率的提高,转折点动剪切模量增加得越快,阻尼比减小得越慢。
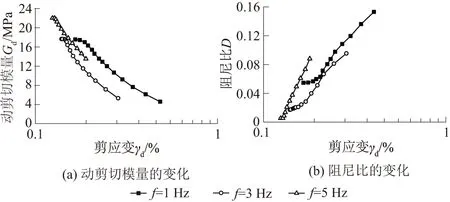
图8 不同加载频率下Gd与D的变化Fig.8 Changes of Gd and D under different loadingfrequencies
分析其原因,动荷载作用下,土粒间的原有连结被破坏。当荷载频率较小时,土粒有充足的时间重新排列组合,塑性变形较大,表现为动剪切模量较小,阻尼比较大;当荷载频率增大后,土粒重组的时间较短,塑性变形有限,耗能较小,表现为动剪切模量增大,阻尼比减小。
4 预测模型及验证
4.1 动剪切模量模型的建立
以上的分析表明动应力幅值、冻融次数、有效围压、荷载频率可以独立地影响粉砂的动剪切模量。张向东等[7]提出了温度、水分和冻融对砂土动弹性模量、阻尼比的影响关系式,在此基础上本文采用多种因素对粉砂土的最大动剪切模量进行修正,关系式为
Gd,max=αAαnασαfGd,0。
(5)
其中,
式中:αA、αn、ασ、αf分别为动应力幅值、冻融次数、有效围压、荷载频率的修正系数,Gd,0为基准条件(试样S-1)时的最大动剪切模量。
根据式(5),对试验结果回归分析,得出
546(1+0.000 1e1.5f)(1.5-0.09e0.03A)。(6)
式中Pa为一个大气压101.3 kPa。
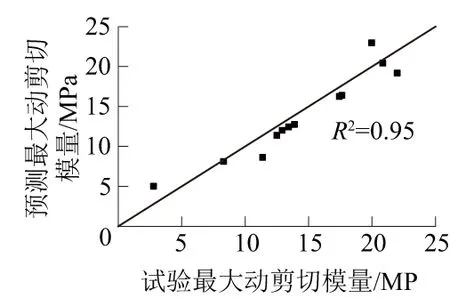
图9 Gd,max预测结果与试验结果的比较Fig.9 Comparisonbetween predicted resultsand test results of Gd,max
最大动剪切模量试验结果与式(6)预测结果的对比如图9所示 。两者有着较好的线性相关性,这说明式(6)可用来估算最大动剪切模量。
Hardin和Drnevich[19-20]提出的双曲线模型不能很好地反映动剪切模量与剪应变的关系,因此本文提出修正Hardin模型Gd函数,即
(7)
式中a、b、c为材料常数。
将式(6)代入式(7),最终得到
Pa0.76(1+0.000 1e1.5f)(1.5-0.09e0.03A) 。
(8)
试样S-4、S-9、S-12的动剪切模量预测值和试验值如图10所示。两者吻合较好,证明式(8)可用来预测不同试验条件下含黏粒粉砂的动剪切模量。
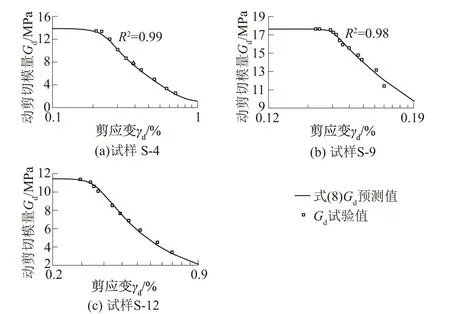
图10 Gd的预测值和试验值与γd的关系Fig.10 Predicted and test values of Gd versus γd
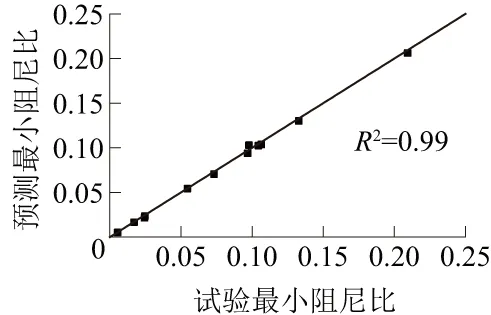
图11 D预测结果与试验结果的比较Fig.11 Comparisonbetween predicted resultsand test results of D
4.2 阻尼比模型的建立
与式(5)相同,提出最小阻尼比经验公式,即
Dmin=βAβnβσβfD0。
(9)
其中,
式中:βA、βn、βσ、βf分别为动应力幅值、冻融次数、有效围压、荷载频率的修正系数;D0为基准条件(试件S-1)时的最小阻尼比。
根据式(9),对试验结果进行回归分析,得到
0.05(-0.9+0.6e0.02A) 。
(10)
最小阻尼比试验结果与式(10)预测结果的对比如图11所示,两者有很好的线性相关性。
同理提出修正Hardin模型D函数,即
D/Dmin=
(11)
式中m、k为材料常数。
将式(10)代入式(11),最终得到
试样S-4、S-9、S-12的阻尼比预测值和试验值对比如图12所示。两者吻合较好,证明式(12)可用来预测不同试验条件下含黏粒粉砂的阻尼比。
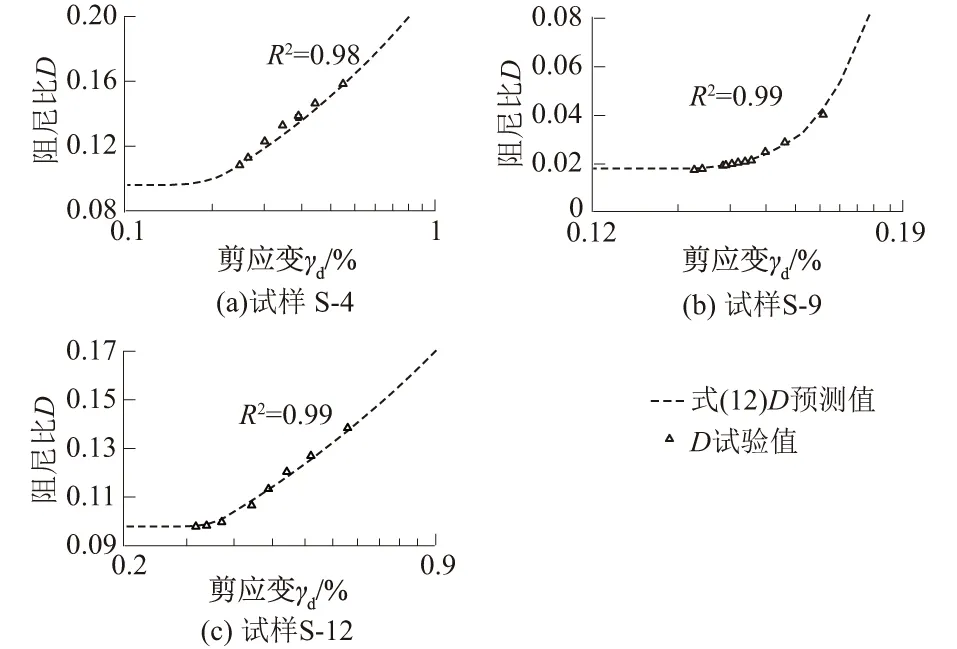
图12 D的预测值和试验值与γd的关系Fig.12 Predicted and test values of D versus γd
5 结 论
(1)未冻融粉砂土动剪切模量随动应力幅值、有效围压、荷载频率的增大而增大。粉砂土的动剪切模量在冻融1次后下降很大,冻融1到10次时逐渐增大,在冻融14次时下降至最小。
(2)未冻融粉砂土阻尼比随动应力幅值、有效围压、荷载频率的增大而减小。粉砂土的阻尼比与剪应变的变化曲线斜率在冻融1次后减小,冻融1到10次时逐渐增大,在冻融14次时下降至最小。
(3)考虑4种因素影响,提出最大动剪切模量与最小阻尼比的经验公式,并证明该经验公式与试验数据吻合较好。考虑冻融循环的非单一化影响,根据冻融次数区间,对经验公式进行了分段。
(4)分别建立粉砂土的动剪切模量、阻尼比与剪应变关系的修正Hardin双曲线模型,该模型可用来预测含黏粒粉砂受冻融次数、动应力幅值、有效围压、荷载频率影响的动剪切模量与阻尼比。

