Karst地区明渠伏流交替河道水动力学模型及应用

李松萍，陶 铭，金中武，胡德超

(1.华中科技大学 水电与数字化工程学院，武汉 430074; 2.长江科学院 河流研究所，武汉 430010)

1 研究背景

在我国西南Karst地区具有特殊的地理地质条件，常常出现明渠与伏流交替型河道。该类型河道的水流运动属于自由水面流动、有压流动的混合流运动，水流形态十分复杂，目前人们对于它们的认识还比较少。与此同时，研究混合流的运动规律也是研究明渠与伏流交替河道物质输移、泥沙冲淤的基础，具有重要科学意义。随着我国西南Karst地区的水资源、水电开发工程逐渐增多，研究Karst地区明渠与伏流交替河道的水流规律可为工程建设提供设计依据和技术支撑，具有重要的工程应用价值。

混合流研究常采用基于圣维南方程或其变化形式的一维水动力模型模拟的方法。已开展的研究多集中在城市地下管网输水领域，现有的混合流模型分为2类。第一类方法采用双控制方程分别描述混合流中自由表面水流和有压水流运动；第二类方法用单控制方程对混合流运动进行统一描述。Bousso等[1]等就上述2类模型优缺点进行过比较，双控制方程模型可以显式追踪水流与空气的分界面，这类模型实现起来较为复杂且不具有适用于各种流态的通用性。单控制方程模型较为简单，但常常需要借助辅助技术(Preissmann slot技术[2]、压力分割技术[3])去描述混合流运动。此外，Casulli和Stelling[4]根据测压管水头在明渠、承压水流中具有相同的表达形式，实现了混合流的统一描述和模拟。

以上混合流模型主要适用于城市管网中规则过流断面(例如矩形、圆形)混合流的模拟。而真实河道断面十分复杂，所以当这些模型用于模拟Karst河流明渠与伏流交替河道时常常遇到困难。目前，对于真实明渠与伏流交替型河道的水流模型的研究还很少。在仅有的文献报道中，Zhang等[5]通过用双控制方程描述的方法建立了明渠伏流一维水流模型。模型通过互提边界条件法实现自由表面水流与有压水流计算的耦合，在伏流段采用恒定流模型计算。他们使用所建立的模型模拟了真实河道不规则地形条件下的混合流。经过文献调研，真实河道不规则地形条件下混合流的统一型模型，至今尚未有文献报道。

本文参考文献[4]根据测压管水头的双重含义实现混合流的统一描述；使用局部线性化水流控制方程代替文献[4]的控制方程，大幅简化了数值离散和求解；在前期规则封闭断面混合流模型[6]的基础上，提出三角形子断面法描述伏流非规则封闭断面，进而建立了真实明渠伏流交替河道的统一型混合流模型。以贵州六冲河夹岩水库为背景，研究了明渠伏流交替河道纵向沿程的流速变化规律以及伏流河段前布置人工隧洞的分流规律。

2 模型简介

2.1 控制方程

使用圣维南方程组作为描述明渠与伏流交替水流运动的控制方程组，其基本形式如式(1)、式(2)所示，其中式(1)为连续性方程，式(2)为动量方程：

(1)

(2)

式中:η表示测压管水头，对于封闭断面过流通道中的承压水流使用其本意，对于自由水面(明渠)水流而言测压管水头的含义即为自由水面高度[4](m)；u为断面平均流速(m/s)；B为断面水面宽度(m)；A为过水断面面积(m2)；g为重力加速度(m/s2)；nm为河道综合糙率值；R为断面水力半径(m)；t为时间(s)；x为距离(m)。

自由水面高度(水位)的物理本质就是测压管水头，前者是后者在明渠水流中的一种具体表达形式。根据测压管水头在明渠、承压水流中具有相同的表达形式，即可使用式(1)、式(2)对混合流的自由表面部分和有压部分进行统一描述。在明渠河段水流为自由水面流动，η为断面水位；在伏流段(充满)时河道为有压流动，η为测压管水头。

2.2 计算网格与明渠及伏流的模型描述

以断面为中心构建控制体(也称单元)，在控制体中心布设水位变量，在控制体界面(边)处布设流量变量。ne和ns分别用于表示单元和边的数量，每个单元/边都有一个唯一的全局单元/边索引。与计算网格(如图1所示)相关联的变量定义如下。对于计算单元i，Δxi表示计算单元的长度；Bi是布置在计算单元中心的横断面的湿表面宽度，它与单元的水位有关并随时间变化；Ai代表位于单元i的横断面的输运面积。对于连接单元i和i+1的边i+1/2，Δxi+1/2是单元i和i+1中心之间的距离；Ai+1/2和Ri+1/2分别为边i+1侧的输运面积和水力半径，由单元i和i+1的值插值得到；i+1/2和i-1/2分别表示第i个单元的后一条边和前一条边。

图1 明渠与伏流交替河道计算网格Fig.1 Computational grids of open channeland sinking stream

伏流和明渠区域中的计算单元用标记(CLO)区分。对于伏流范围内的计算单元，CLO设置为1；对于明渠范围的计算单元，CLO设置为0。在伏流区域，计算单元根据其是否充满进一步区分(用“PRE”标记表示)。对于伏流区域内承压流动的计算单元，PRE设置为1；对于明渠段自由表面流动状态的计算单元，PRE设置为0。在该计算范围中，所有自由表面和承压区域的计算单元同步进行求解。

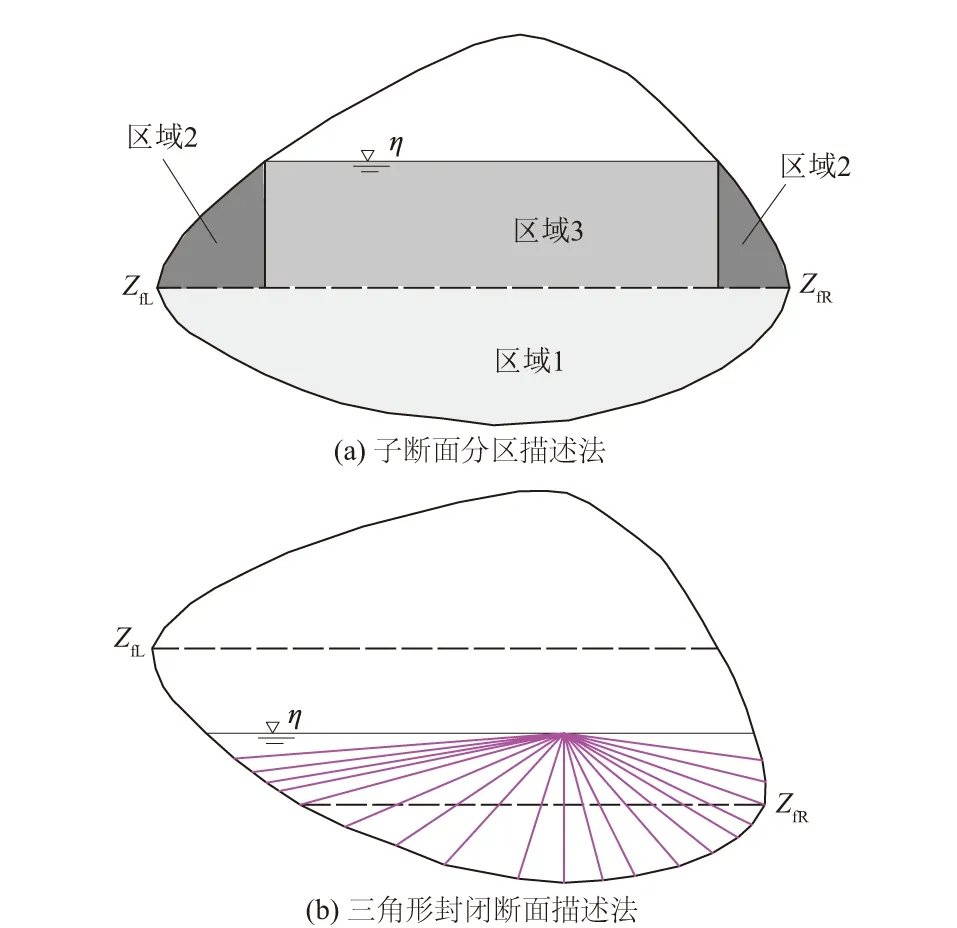
图2 伏流洞非规则封闭断面的描述方法Fig.2 Descriptions of the irregular closed cross-sectionof a sinking stream

伏流非规则封闭断面的描述方法。使用传统的子断面法描述非规则封闭断面(图2(a))，需要进行分区描述，这种分区描述十分复杂，且分区可能需要随着洞内水位的变动而调整；当封闭断面左右两侧转折点ZfL、ZfR处于不同高度时，会引起描述困难和不准确。初步测试表明，基于传统子断面分区描述法的非规则封闭断面混合流模型，常常出现计算不稳定或不准确的问题。本文提出三角形封闭断面描述法，来解决这一问题。当过流断面处于充满状态时，过流断面面积等于断面最大面积；当处于非充满状态时，断面过流面积的计算方法(图2(b))：在断面最低点处竖直向上引一条线段与水面相交，得到一个交点，依次将水下所有断面点与该交点连接，于是形成一系列三角形，通过计算各三角形面积并进行求和，即可得到过流面积。

2.3 数学模型框架

混合使用有限差分法和有限体积法对模型的控制方程进行离散。使用半隐方法离散压力梯度项，使用欧拉-拉格朗日法[7](ELM)求解控制方程中的对流项；联合动量方程和连续性方程构建三对角阵求解各控制体压力；将压力代入动量方程确定最终流速或流量。

2.3.1 控制方程的离散

对于明渠和伏流这2种流动形态，采用θ半隐式方法[8-9]对动量方程的水位梯度项进行离散在边i+1/2处，动量方程可统一离散为

式中:θ为隐式因子；Δt为时间步长；上标n表示n时刻；ubt为用ELM求解动量方程对流项后得到的结果。河床阻力项采用ubt和un+1进行离散，以提高计算稳定性。

当离散的动量方程中所有显式项合并后，仅剩下未知项(n+1时刻的压力ηn+1)，进一步将式(3)转换为

(4)

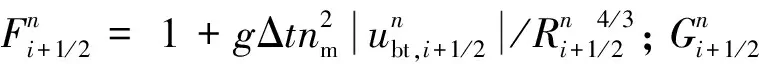
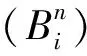
(5)

式中Δxi表示第i个单元的长度。

2.3.2 速度-压力耦合的求解

采用ELM求解得到动量方程对流项和局部线性化连续性方程对流项的方法，连续性方程和动量方程的耦合解只需要求解一个线性问题，将式(4)代入式(5)进行速度-压力耦合，得到

(6)

其中，

式中a、b、c分别表示对应单元i-1、i、i+1的系数项。

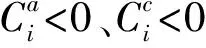
2.3.3 枝状、环状河网的预测-校正法

在实际中，河道常常并不是单一的而是多条纵横交错构成河网，呈枝状、环状形态。此时，采用预测校正法[10-11]实现河网各支汊的耦合求解，在保证计算精度的前提下能有效提高计算速度。河网模拟的预测-校正法以汊点为界将河网分成若干段，分为预测步和校正步进行求解。

2.3.4 测试案例

该试验中水平管道连接2个水库，有压流动发生在水平管道中，如图3所示。管道长L=400 m，正方形截面面积a=1 m2。管道中间设有一个关闭的闸门，2个水库的水位分别为η1和η2且保持不变，水位差η1-η2=1 m。

图3 水平有压管段连接2个水库Fig.3 Two reservoirs connected by a horizontalpressurized pipe

当t=0时，闸门突然打开。假定管道无摩擦，流速和管道内压力用解析解描述为：

u(x,t)=u0tanh(t/t0) ,

(7)

在该算例中，忽略水的可压缩性和管壁弹性，即上游到下游的流量相等。在逐渐缩小的均匀网格上对模型进行测试，网格尺度dx依次为40、20、16、10、5 m，建立解的网格独立性。该模型稳定地完成了所有的模拟。随着网格尺度变小，计算结果逐渐收敛于解析解，如图4。当网格尺度≤16 m时，计算结果稳定趋近于解析解，体现了网格无关性。

图4 管道内第一个网格点不同网格尺度下速度和压力的模拟结果Fig.4 Simulated results of velocity and pressure at thefirst grid point inside the pipe (using different grid scales)

3 模型应用

夹岩水利枢纽工程位于贵州省毕节市与遵义市境内，主要涉及的河流有六冲河以及3条支流：大河、挖嘎河和引底河。大坝位于乌江支流六冲河中游河段上，该段河谷深切，岩溶相当发育，属于典型的Karst地貌。拟建夹岩水库库区河流明暗相间(如图5)，有多处伏流段(大、中、小天桥伏流段)，为典型的明渠伏流交替河道。应用本文建立的明渠与伏流交替河道水动力学模型，研究不同工况条件下六冲河干流沿程的流速变化规律以及人工隧洞的分流能力。

图5 夹岩水库干支流、伏流及人工隧洞布置Fig.5 Arrangement of main stream,tributary,sinkingstream and artificial tunnels in Jiayan Reservoir

3.1 夹岩水库明渠伏流水动力模型建模与测试

夹岩水库数学模型的计算区域如图5，包括六冲河(到坝址段)、支流(大河、挖嘎河和引底河)，其中六冲河干流的大、中、小天桥段为伏流段。平面上呈现为枝状河网形态，在数学模型建模时，将计算区域分为7个河段。采用200 m尺度的计算网格对计算区域进行剖分，得到241个计算单元。利用散点地形对断面地形进行插值，在伏流段的33个断面采用设计单位提供的实测断面地形资料。

采用实测水文资料和设计单位提供的河道糙率资料对模型进行测试。计算区域内有七星关水文站，位置见图5。数学模型的入流边界为4个：六冲河、大河、挖嘎河与引底河，出流边界为一个，即坝址。由于模型的各支流入口均没有实测入流资料，故采用如下方法设计测试的边界条件。根据实测水文资料，将七星关站日流量实测数据采用同比放大法得到对应坝址日流量。坝址以上流域集水面积为4 312 km2，大河流域面积为1 195 km2，挖嘎河流域面积为1 195 km2，引底河流域面积为535 km2。采用流域面积比例法得到六冲河与大河流量分配系数分别为0.60与0.40；根据流量守恒定理与流域面积比例法得到挖嘎河与引底河流量分配系数分别为0.38与0.62。

采用2000年水文过程、设计单位提供的糙率进行模型测试。根据水文资料，河流多处于平水年，2000年为典型平水年，选择该年具有普适性。河床糙率取值在0.055～0.06，在该糙率条件下，将七星关站的实测值与计算值的流量过程进行套绘，如图6，实测和计算的流量过程未出现相位偏移，该站的流量相对误差在1.6%以内。表明本文数学模型计算方法可行，参系数取值合理，可用于计算和研究该河段的水流特性。

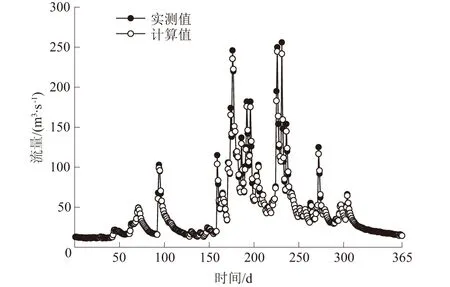
图6 七星关站模拟值与计算值的流量过程Fig.6 Flow rate processes at Qixingguan station frommodel test and computation

3.2 干流沿程的流速变化规律

由于夹岩水库泥沙问题较为突出，设计部分对库区伏流洞是否会被淤堵较为关心。水流流速是泥沙是否淤积的重要判断指标，因此本节开展了六冲河干流沿程的流速变化规律模拟研究。采用恒定水流边界来研究六冲河干流沿程流速变化规律，入流边界选择枯季流量、多年平均流量以及洪峰流量3种工况，坝前水位均为正常蓄水位1 323 m。第1种工况各开边界流量分别为4.0、2.7、1.8、3.0 m3/s；第2种工况各开边界流量分别为22.9、15.1、7.4、12.2 m3/s；第3种工况各开边界流量分别为425.3、281.7、106.4、174.0 m3/s。3种工况七星关的流量分别为6.7、38.0、707.0 m3/s。

3种工况下干流纵向沿程的流速变化曲线如图7。流速随着河道断面面积的变化而变化，在进入大、中、小天桥伏流段时由于断面面积骤减而流速增加。由于该河流位于山区峡谷，过流断面多变，流速呈现起伏变化。在第1种工况下，干流明渠段与伏流段流速均在0.02 m/s以下；在第2种工况下，干流明渠段流速在0.02 m/s以下，伏流段流速在0.1～0.2 m/s；在第3种工况下，明渠与伏流段流速差异显著，明渠段流速一般在0.25 m/s以下，伏流段流速一般在1.0～3.0 m/s。

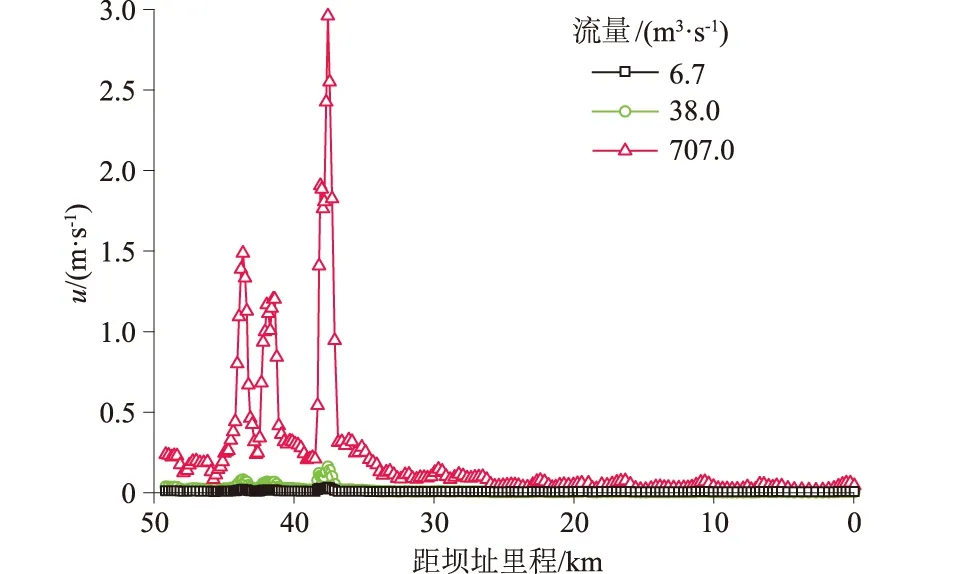
图7 干流沿程的流速变化Fig.7 Variation of flow velocity along the main stream

3.3人工隧洞的分流能力

夹岩水库库尾共有3段伏流河段，分别为大、中、小天桥伏流段。由于伏流段可能存在断面小过洪能力不足的情况，加之水库蓄水后可能存在泥沙淤堵风险，产生不利影响。因此，设计单位布置了伏流段分洪隧洞以解决泄洪问题。

伏流段分洪隧洞分布在大中天桥和小天桥河段，每段由2条隧洞并列组成，隧洞断面均为12 m×16.5 m的城门洞，顶拱中心角120°。分别将2条隧洞合并布置，宽度加倍(24 m)，隧洞的平面布置见图5。大中天桥隧洞长2 843 m，进口底板高程1 315.980 m，底坡α=0.008，出口高程1 313.706 m；小天桥隧洞长603 m，进口底板高程1 310.732 m，底坡α=0.008，出口高程1 310.250 m。隧洞按无压流设计，过流能力按明渠均匀流计算。加上人工隧洞后，计算区域在平面上呈现为环状、枝状河网混合形态。

图8 1971—1990年大中天桥、小天桥隧洞和伏流段流量过程Fig.8 Flow processes of artificial tunnels and sinkingstreams in front of big-medium and small overbridgesfrom 1971 to 1990

为阐明人工隧洞的分流能力，开展了河网水动力模拟研究。计算时，河道糙率使用设计单位提供的数据0.055～0.06，隧洞糙率取设计值0.014。1971—1990年期间水文资料完整，包含平水年、丰水年、枯水年等各种典型水文年份，能较全面地代表该河段水文条件，故采用1971—1990年作为人工隧洞分流过程计算的系列年。大中天桥、小天桥人工隧洞及大中天桥、小天桥伏流段的流量过程如图8所示。大中天桥伏流前的人工隧洞的分流比为40.3%～42.8%，小天桥伏流前的人工隧洞的分流比为76.8%～78.6%。从20 a水文过程模拟的统计数据来看，大中天桥隧洞分流量为90 622.7 m3/s，占河道总流量的32.7%；小天桥隧洞分流量为197 150.3 m3/s，占河道总流量的70.7%。

4 结 论

(1)基于圣维南方程组，根据测压管水头在明渠、承压水流中具有相同的表达形式，实现了自由水面水流、承压水流的统一描述。提出三角形子断面法描述伏流非规则封闭断面,建立了适用于真实Karst地区明渠伏流交替河道的统一型混合流模型。采用半隐方法离散压力梯度项，使用欧拉-拉格朗日法求解对流项，并使用预测-校正法实现了枝状、环状河网各支汊的耦合求解。

(2)开展了贵州六冲河夹岩水库明渠伏流交替河段(包含有大中天桥、小天桥伏流)的数学模型建模。将计算区域划分为7个河段，剖分成241个计算单元。采用2000年水文过程对数学模型进行了测试，水文站的流量计算误差在1.6%以内，表明本文数学模型计算方法可行，参系数取值合理，可用于研究该河段的水流特性。

(3)采用典型水流条件(枯季、多年平均、洪峰流量)，研究了六冲河干流纵向沿程的流速变化规律。在洪峰流量条件下，明渠与伏流段流速差异显著，明渠段流速一般在0.25 m/s以下，伏流段流速一般为1.0～3.0 m/s，有利于伏流过流通道的保持。

(4)采用1971—1990年水文过程，研究了伏流河段前布置人工隧洞的分流规律。大中天桥伏流前的人工隧洞的分流比为40.3%～42.8%，小天桥伏流前的人工隧洞的分流比为76.8%～78.6%。从20 a水文过程的模拟结果来看，大中天桥隧洞分流量占河道总流量的32.7%；小天桥前人工隧洞分流量占河道总流量的70.7%。由此可推测，小天桥隧洞分流将大幅减小小天桥伏流洞内的流速，加速泥沙淤堵。