胶凝砂砾石筑坝材料VC值试验敏感性分析

赖 韩，王瑞骏，李 阳，熊小斌，张 旭，郁宁宁，雷 妍

(西安理工大学 省部共建西北旱区生态水利工程国家重点实验室，西安 710048)

1 研究背景

1970年，Raphael[1]在会议上首次提出对称重力坝(“最优重力坝”)的概念。直至1992年，法国的Londed[2]在国际大坝委员会(ICOLD)第117号公报中发表了“对称硬填料面板坝(Faced Symmetrical Hardfill Dam)”的论文，同年日本学者提出梯形胶结砂砾石(Cemented Sand and Gravel，CSG )坝的概念并开始应用到围堰工程。1993年，希腊建成了世界上首座根据对称硬填料筑坝理念修筑的Marathia坝，坝高28 m，上下游坡比为1∶0.5，水泥用量仅70 kg/m3。“基于硬填料坝和梯形CSG坝的理念和实践，贾金生等于2004年提出胶结砂砾石坝(CSGRD)概念，街面、洪口等胶结砂砾石围堰分别于2004年、2005年建成。并于2009年提出了胶结颗粒料坝的概念，目的在于修建更安全、更经济的环境友好的大坝。该坝型包括胶结砂砾石坝(曾用名胶凝砂砾石坝)、堆石混凝土坝(或胶结堆石坝)和胶结土坝”[3]。CSGRD是一种漫顶不溃，主要应用于河床砂卵石丰富的地区，单位水泥用量比碾压混凝土(RCC)坝低，兼有土石坝和混凝土坝两者优点的新坝型[4]。目前，日本已建成5座CSG永久坝，在建的有两座(Apporo dam和Sanru dam)[5]。中国首座CSGRD——坝高61.6 m的山西守口堡工程于2019年底完工。钟登华等[6]、马洪琪等[7- 8]采用全球定位系统(GPS)，通用无线分组业务(GPRS)和掌上电脑(PDA)技术实现施工现场实时质量监控并在糯扎渡心墙堆石坝工程成功应用，后续在拉西瓦、锦屏一级、南水北调工程和龙开口RCC坝等重大水利工程也得到成功应用。然而制约CSGRD发展的关键技术难点主要在于施工工艺、拌合碾压设备及施工全过程质量控制[9]。施工中仓面的胶凝砂砾石(CSGR)的压实度受骨料级配、砂率、维勃稠度(VC值)等参数影响，抗压强度又主要受胶凝材料用量以及用水量的影响[10]。因此，施工全过程质量控制尤为重要。

在工程上主要应用维勃稠度来评定拌合物的工作性能是否符合混凝土的施工要求，VC值太小表示拌合料太湿，振动碾易沉陷，影响正常工作；VC值太大则拌合料太干，灰浆太少，骨料架空，不利于压实。在施工上低VC值的CSGR对可塑性、可碾性、层间结合能力和抗骨料分离的能力有利，但过高的单位用水量在降低VC值的同时还会增大水胶比并降低CSGR抗压强度。金光日等[11]采用正交试验法，研究表明掺PVA纤维能提高CSGR力学性能，试件由脆性破坏转变为延性破坏。刘玉玺等[12]、钟桂良等[13]在RCC坝施工时对仓面不同施工气候(温度、相对湿度和风速)影响下的VC值进行实时监控控制，从而及时调整施工措施，保证施工质量。刘东海等[14-15]提出基于压实功的不同VC值下的施工碾压参数控制标准，严格监控施工质量。上述研究均未涉及CSGR材料本身配合比对VC值产生的影响，而配合比中单位水泥用量(C)、单位粉煤灰用量(F)及砂率(S)的取值大小在一定程度上影响了适合拌合物工作性能的最优单位用水量(W)[10]。本文通过统计通用软件MINITAB设计考虑交互作用的四因素三水平正交试验，共27组配合比，研究CSGR的VC值关于W、C、F和S四个影响因素的敏感性分析，研究结果对CSGR施工中配合比优化设计具有重要指导意义。

2 正交试验设计

2.1 原材料

水泥为海螺牌42.5R普通硅酸盐水泥，Ⅱ 级粉煤灰需水量比为101%，细骨料为细度模数2.8的河砂，含水率为2%；粗骨料为二级配天然卵石，小石(5～20 mm)和中石(20～40 mm)的质量比为3∶1(其中粒径5～10 mm：10～20 mm质量比约为1∶2)，堆积密度分别为1 711 kg/m3和1 665 kg/m3。外加剂为聚羧酸系高性能减水剂，掺量为胶凝材料总量的1%。

2.2 配合比设计

参照《胶结颗粒料筑坝技术导则》(SL 678—2014)[16]，配合比设计参数应满足：胶凝材料用量不宜低于80 kg/m3，水胶比宜在0.7～1.3，砂率宜在18%～35%，掺合料掺量宜在40%～60%。设计考虑W与C、W与F及W与S间交互作用的四因素三水平的正交试验，因素水平见表1，正交设计见表2，最终配合比及VC值试验结果见表3。

表1 四因素三水平的正交试验Table 1 Orthogonal test with four factors and three levels

2.3 试验方法

本试验采用HJW-30型数显混凝土搅拌机，原料拌合方法步骤为：①投入砂、水泥和粉煤灰后干拌30 s；②加入1/2的水湿拌30 s;③加入卵石和剩余的混合着高性能减水剂的1/2的水湿拌180 s后搅拌机自动停止搅拌，静止10 s后卸料。参照《普通混凝土拌合物性能试验方法》(GBJ80—85)[17]，试验应用维勃稠度法测VC值，采用VBR-2数显维勃稠度仪，适用于骨料最大粒径≤40 mm的混凝土拌合物稠度测定。

表2 L27(313)正交表Table 2 L27(313) orthogonal table

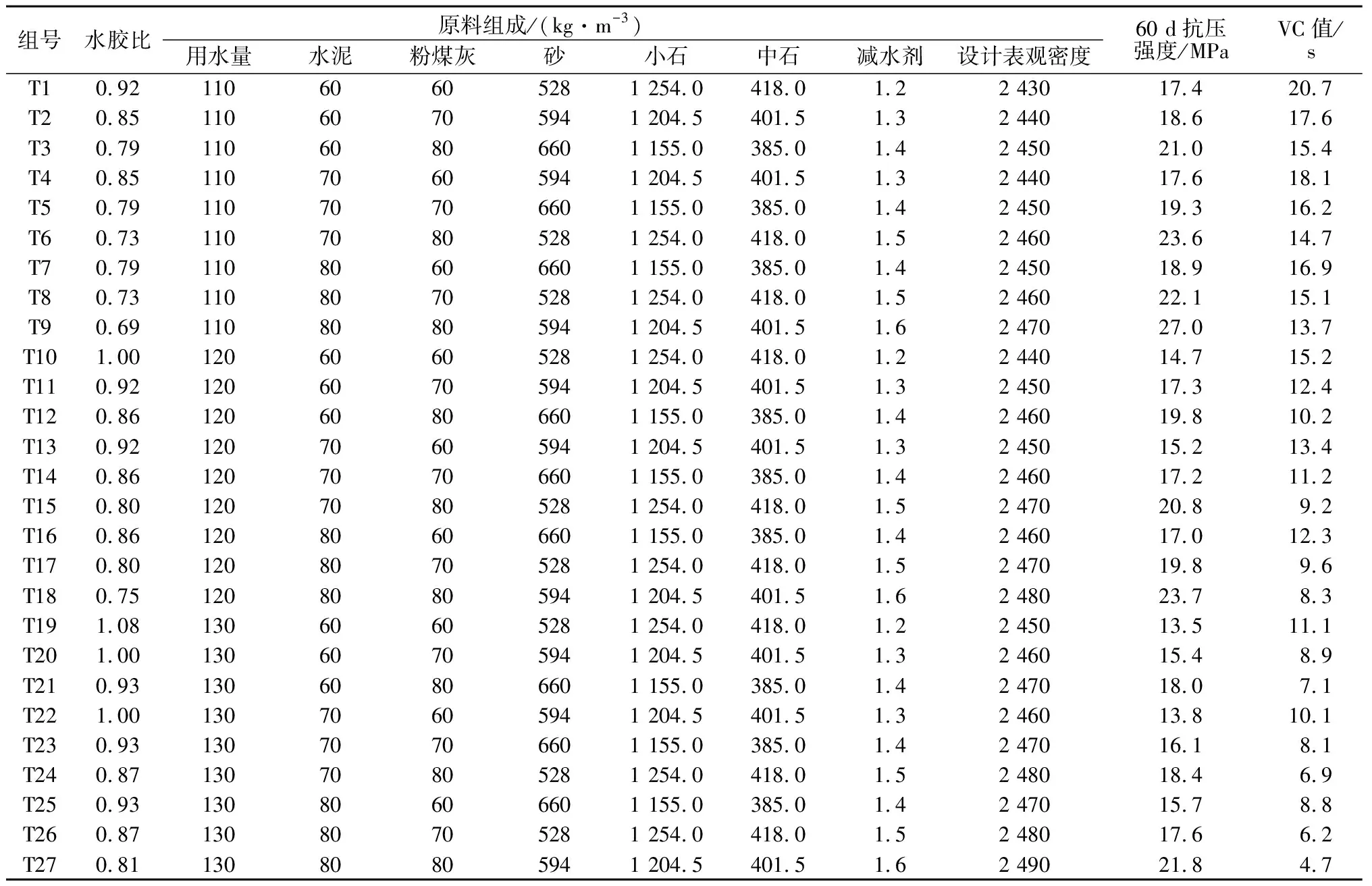
表3 CSGR配合比及VC值试验结果Table 3 Mixture ratio of CSGR and VC value results

3 结果与讨论

3.1 单位用水量对VC值的影响

试验考虑3个水平的单位用水量110 kg/m3(T1—T9)、120 kg/m3(T10—T18)、130 kg/m3(T19—T27)对VC值的影响，不同单位用水量下的VC值变化见图1，同一试验系列表示除了单位用水量外其他因素均相同，不同试验系列除了单位用水量相同外其他因素各有差异。

图1 不同单位用水量下的VC值变化Fig.1 Change of VC value under varied unit waterconsumption

从图1可知，不同单位用水量的VC值变化曲线近似平行，说明VC值的变化和单位用水量基本呈线性关系。同一单位用水量下的VC值呈“锯齿状”变化，单位用水量为110、120、130 kg/m3时VC值分别在平均值16.5、11.3、8.0 s上下波动。试验系列1中VC值最大值20.7 s(T1)与最小值11.1 s(T19)差值最大，试验系列6中VC值最大值14.7 s(T6)与最小值6.9 s(T24)差值最小。近似地推测单位用水量每增加1 kg/m3，VC值降低0.39～0.48 s，而RCC的VC值降低0.67～1.15 s[18-19]，表明CSGR筑坝材料VC值对单位用水量的敏感度低于RCC，一方面是CSGR的胶凝材料用量更少，另一方面是CSGR粗骨料采用的是卵石，更不易于和砂浆黏结。

3.2 极差分析

极差分析包括计算和判断2个步骤，极差是试验指标值(VC值)关于某因素同一水平平均值的最大值与最小值的差值。极差越大，表明试验因素在试验高低水平范围内变化时，对试验指标值的影响越大，由此可以判断影响因素主次顺序、影响因素最优水平以及最佳因素水平组合。根据27组配合比正交试验VC值实测结果，进行极差分析，作影响因素和VC值均值之间的趋势图(见图2)，对VC值与各因素水平波动的关系进行直观分析。

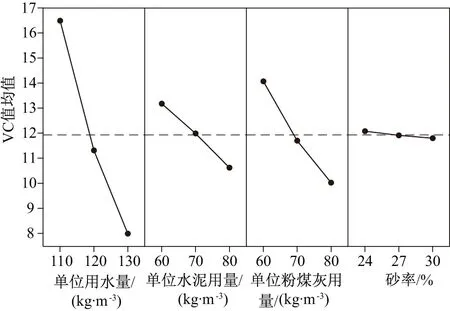
图2 极差分析结果Fig.2 Results of range analysis

从图2可知，试验因素对VC值影响的主次顺序为单位用水量>粉煤灰用量>水泥用量>砂率。从指标效应上看，VC值越小越有利于CSGR施工，因此得到单位用水量、单位水泥用量、单位粉煤灰用量和砂率的最优水平依次为130、80、80 kg/m3和30%，推测最佳的试验配合比组合为W3C3F3S3，该配合比组不在试验组范围。进一步补充W3C3F3S3配合比试验以验证，实测VC值为4.9 s，比试验组第27组W3C3F3S2高0.2 s，因此极差分析方法虽有一定的可信度，但并不精确，且人为、环境等影响因素也会对试验造成结果上的误差。

3.3 方差分析

由于极差分析法不能准确估计试验结果测定中存在的必然误差。为区分试验误差(即组内误差)与各因素水平变动(即组间误差)引起测试结果的差异，并确定因素对试验结果的显著性作用差异，采用方差分析法对VC值测试结果进行分析。VC值方差计算分析见表4。

表4 VC值方差分析结果Table 4 Variance analysis result of VC value

根据表4方差分析结果，查F分布表可知，F值>F0.01(2,18)=6.01表示因素高度显著，F值>粉煤灰用量>水泥用量>>砂率，砂率对VC值的影响作用等同于误差因素几乎可以忽略。原因是VC值本身对用水量高度敏感，因此有必要研究施工气候(温度、相对湿度和风速)对VC值的影响[12-13]；而粉煤灰比水泥细，且粉煤灰有润滑作用改善了拌合物工作性能；3%的砂率水平梯度太低，加上室内试验是小容量拌合，与现场试验区别大，导致砂率对VC值的影响作用下降，也可能是3个砂率水平本身很接近最优砂率。

根据方差分析结果并绘制因素间VC值交互作用图见图3。交互作用图[20]是在一个因素水平始终保持恒定时另外一个因素的均值图，图中两直线平行，表示因素间交互作用不显著，图中两直线相交表示两因素间交互作用显著。

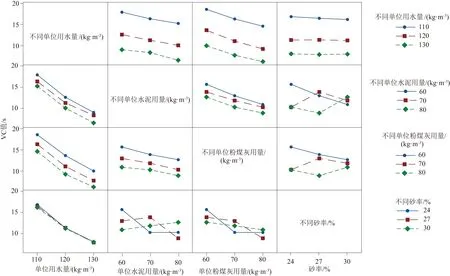
图3 不同因素间的VC值交互作用图Fig.3 Interactions among different factors

由图3可以看出，用水量与水泥用量、粉煤灰用量和砂率之间交互作用不显著，水泥与粉煤灰用量之间交互作用不显著，砂率与水泥、粉煤灰用量之间存在明显的交互作用。原因是水泥和粉煤灰均属胶凝材料，对水胶比大小的影响作用相同；而不同用量的水泥、粉煤灰与砂作用直接影响了砂浆的产量。通过横向各行对比，说明改变单位用水量对VC值的影响作用最显著；纵向各列对比也表明改变单位用水量对VC值的影响作用最显著，从第一行和第一列的最后一个图即水与砂率交互作用图可知，在相同用水量的情况下，砂率变化对VC值的影响不显著。

3.4 多元线性回归预测模型

一元线性回归是一个主要影响因素作为自变量来影响因变量的变化，而在现实研究问题中，往往是2个以上的影响因素作为自变量来影响因变量的变化，这时需要采用多元线性回归预测模型。基于最小二乘法原理，建立VC值与影响因素W、C、F和S之间的多元线性回归数学模型，然后用各影响因素的假定值推算出VC值的预测值，这对工程实践具有有效的指导意义。基于27组VC值实测结果，进行多元线性回归得到数学预测模型(1)和预测模型(2)，预测模型中的4个因素W、C、F和S在各自因素最低水平1和最高水平3之间取值。

VC值=87.28-0.425 0W-0.127 8C-

0.202 2F-0.046 3S,R2=0.980 1

(1)

VC值=86.03-0.425 0W-0.127 8C-

0.202 2F,R2=0.979 3

(2)

3.5 残差分析

残差是回归模型预测值与实测值的差值，通过残差分析有利于确定回归模型能否用于实际预测。通过残差分析，VC值实测值及预测模型(1)和预测模型(2)的预测值见表5，并绘制预测模型(1)和预测模型(2)的残差图见图4和图5。

表5 VC值的实测值和模型预测值Table 5 Measured and model-predicted VC values

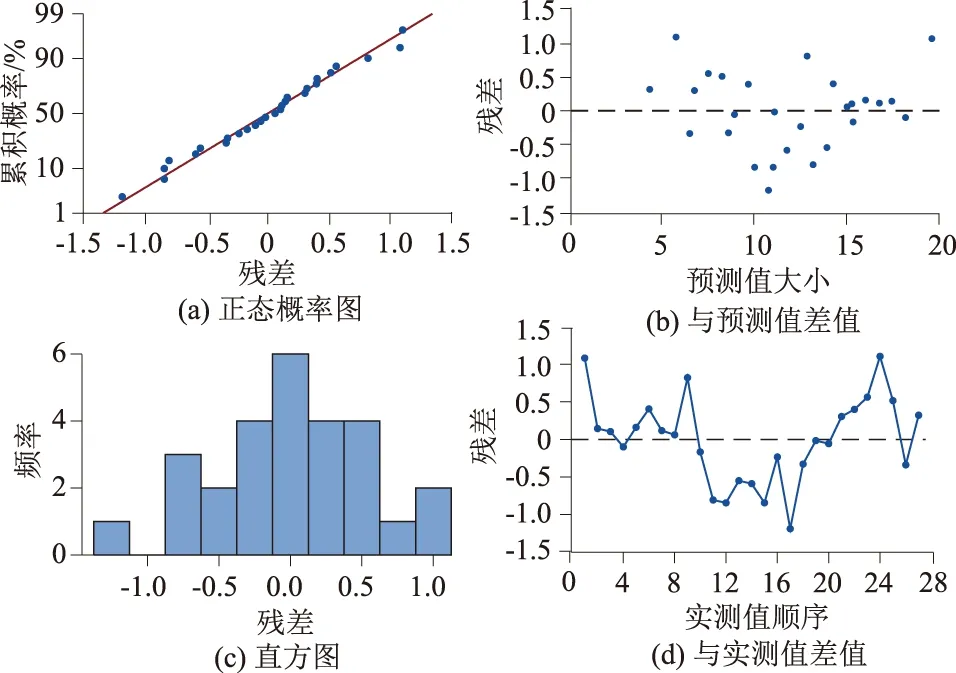
图4 预测模型1的VC值残差图Fig.4 Residual plot of VC value of predictionmodel 1

图5 预测模型2的VC值残差图Fig. 5 Residual plot of VC value of predictionmodel 2

图4和图5的残差正态概率图中，数据点基本呈一直线，表明预测值呈正态分布；与预测值差值中，数据点在参考线(Y=0)的上下两侧波动，没有呈现特别的趋势，说明预测模型用于实际预测是恰当的；残差直方图及与实测值顺序图直观地反映了预测值与实测值的差值分布范围及差值大小。残差分析结果表明2个模型都能用于实际预测，显然预测模型1精度更高，但根据极差分析和方差分析结果，砂率在24%～30%变化范围内对试验VC值的影响作用很小，几乎等同于试验误差，可以忽略不计，故选择预测模型2更方便用于实际预测。

3.6 等值线图

根据正交试验结果进行统计分析计算，绘制VC值与任意2个影响因素的等值线图，见图，直观地反映出VC值随因素水平的改变而出现的变化趋势。

从图6(a)—图6(c)可以看出，单位用水量是影响VC值的主要因素，图6(a)和图6(b)表明在相同的用水量下，随着水泥、粉煤灰用量的增大,VC值有降低的趋势，且粉煤灰对VC值的作用比水泥显著。图6(c)直观地反映了在相同用水量下，改变砂率对VC值影响作用不显著。图6(d)表明随着胶凝材料总量的增大,VC值有降低的趋势。此外，根据等值线图能快速锁定目标VC值下的相关因素水平范围。

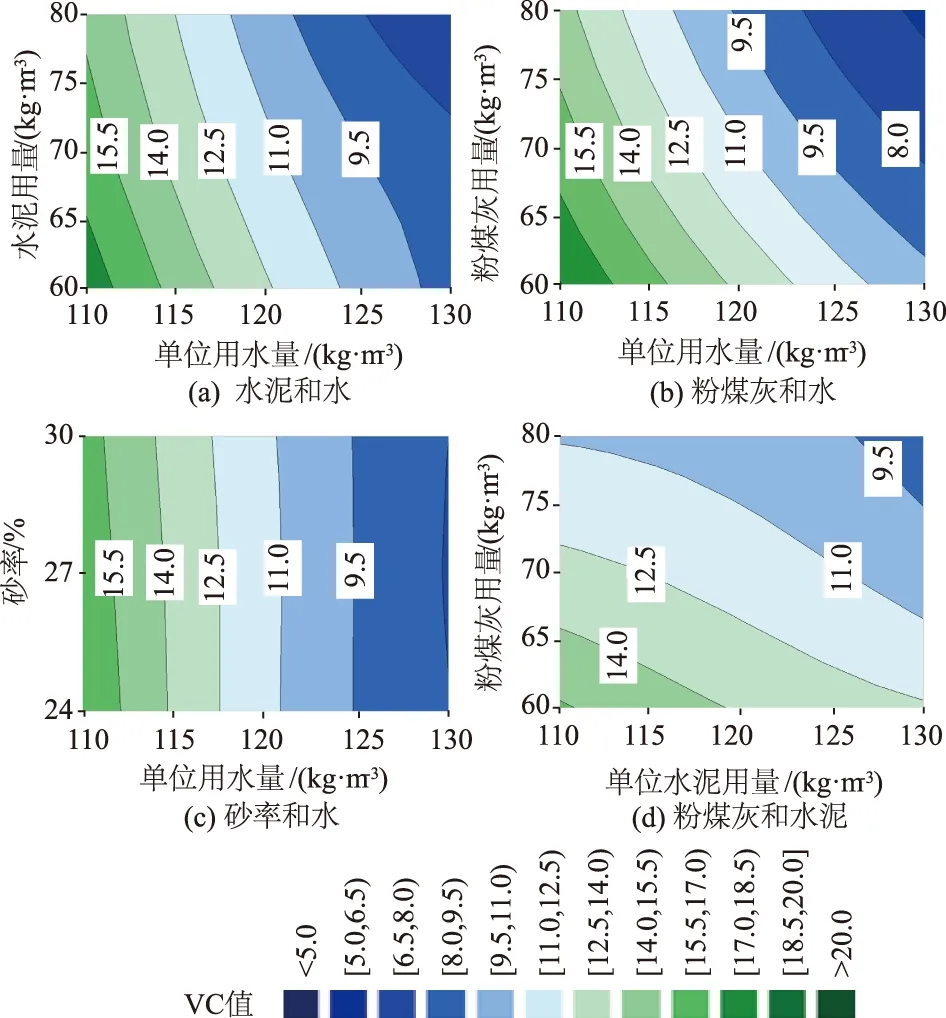
图6 VC值与任意2个影响因素的等值线图Fig.6 Contours of VC value against two randominfluencing factors

4 结 论

(1)VC值的变化和单位用水量基本呈线性关系。单位用水量每增加1 kg/m3，VC值降低0.39～0.48 s，而碾压混凝土的VC值降低0.67～1.15 s。

(2)通过极差分析可知，对VC值影响的主次顺序为单位用水量>粉煤灰用量>水泥用量>砂率，最优水平依次为130 kg/m3、80 kg/m3、80 kg/m3和30%，推断最优配合比组合为W3C3F3S3。

(3)通过方差分析，用贡献率定量分析因素的显著性可知，单位用水量、水泥用量、粉煤灰用量、砂率及误差对VC值的贡献率依次为75.55%、6.73%、17.00%、0.08%和0.64%，因此施工中应严格控制单位用水量，砂率从24%增加到30%对VC值的作用等同于误差因素，几乎可以忽略。

(4)通过多元线性回归得到数学预测模型：VC值=(86.03～0.425 0)×单位用水量-0.127 8×单位水泥用量-0.202 2×单位粉煤灰用量。结合残差分析并综合极差、方差分析结论，该数学模型可用于本次试验四因素共同作用下因素从低水平到高水平范围区域的实际预测，这对实际工程施工时配合比优化设计具有指导性意义。