径流过程分维数与其主要影响因素的定量研究

张 登，崔晨风，陈 刚，李云格

(西北农林科技大学 水利与建筑工程学院， 陕西 杨凌 712100)

分形理论主要研究自然界的不规则现象及其内在规律，其核心是自相似性，这种自相似性具有广泛深刻的含义。而分维数正是衡量自相似性的定量参数，使定量描述复杂几何形体成为可能。

在河川径流的分形特征研究方面，2013年，Bunde Armin等讨论了降水和河流流量的线性与非线性长期相关性及其对风险估计的影响。2014年，李建林等[1]提出R/S灰色预测模型，在径流量预测领域更进一步。2015年，魏炜等[2]运用分形方法对广西澄碧河水库汛期进行分期，拓宽了分形应用领域。2017年，Gires等[3]在城市水文学的特定背景下使用分形工具，分析了来自五个欧洲国家的10个城市或郊区集水区的地表和下水道数据。同年，姜英慧[4]在辽宁西部一区域采用分形理论定量化分析了其水文要素时空变异特征，做出一定研究成果。2018年，邹宝裕等[5]通过计算径流节点分形维数,对径流节点分形特征与侵蚀产沙的相关性进行了探究。2018年，García-serrana等[6]通过阐明分形方法的相关性，来了解表面粗糙度与陆上流型的关系。2018年，Gires等[7]在巴黎地区使用标度定律，更具体地使用通用多重分形来分析模拟地表径流。2019年，王小杰等[8]以渭河流域为研究区域，采用Mann Kendall非参数检验、分形理论和R/S等方法分析渭河干流6个典型水文站多年径流时空变化特征、持续性及两者之间的关系。2019年，Gaidukova[9]探讨了将一系列河流分形维数的相关类型与地表气温的气候规范联系起来的规律性。运用分形理论的研究颇多，但是，在运用分形方法来耦合环境因子并得出定量关系式，同时应用到以表征植被覆盖为主要指标的生态环境状况方面的研究还显不足，本文从此出发，希望做出一点贡献。

径流过程线的复杂程度可以用分维数来表示。而降水能显著影响径流过程，是影响径流过程的首要自然因素[10-11]。同时，植被覆盖率对河川径流也有很大的调节作用, 森林植被能够保持水土, 使分维数减小[12]。另一方面，植被覆盖率是一个地区生态环境状况的重要标志，具有一定的代表性[13]。可见，径流过程分维数在很大程度上可以表征区域的生态环境状况。海拔高度，地面坡度，地表岩性,土壤等因素也会对径流过程产生影响[14]，但是在泾河流域内，相对来说并不是主要因素，所以暂不予讨论。综上, 研究泾河流域径流过程的分形特征并在此基础上研究其与主要影响因素的定量关系，从而可以建立用分维数表征一个地区或同一地区不同年份的生态系统状态的关系式，这存在理论上的可行性。

1 流域概况及资料来源

泾河是渭河的第一大支流，发源于宁夏六盘山腹地，地处陕甘宁边界，全长455.1 km，流域面积45 421 km2，年平均径流量2.140×109m3。泾河流域位于黄土高原中部(106°14′～108°42′E，34°46′～37°19′N)，深处大陆，为典型的温带大陆性气候，处于温带半湿润气候向温带半干旱气候的过渡地带，冬季干旱少雨，夏季多暴雨。据流域各气象站点多年观测资料，流域多年平均气温8℃，年降水量在350 mm～600 mm之间，主要集中于夏、秋汛期季节的5月—9月，这段时间内降水量可占年降水总量的72%～86%；冬春季降水稀少。

泾河流域水文站点众多，如西峡、沙塘川、张家山等。通过观察各测站的分布，发现张家山测站很好地反映了整个流域的径流状况。故在本文研究过程中，选用张家山站测得的水文资料作为研究对象。

本文选用的径流数据为泾河流域张家山水文测站1982年—2016年共35 a的月均径流数据，皆来自于已公布的水文年鉴；流域内选用的环县、崆峒、长武气象站日降雨资料来自中科院水土保持研究所建立的黄土高原生态环境数据中心，同样取1982年—2016年；选用的NDVI遥感图像(1982年—2016年)来自于法国SPOT卫星，空间分辨率为1 km，时间分辨率为10 d。

2 泾河分形特征

2.1 分维数的计算

关于分维数的计算研究颇多，比如，Gangepain提出的盒子法，Mandelbrot的随机游走法以及Pentland的频域法等。通过对比，本文决定采用伯恩公式。Bowen于1979年提出该法并应用于计算类圆形的豪斯多夫维数[15]，具体介绍如下：

设Ψ是一个无孤立点的紧度量空间，f：Ψ→Ψ是一个连续满射，同时f满足开映射且均匀展开，在每一点的共形导数Df存在，那么

(1)Ψ的豪斯多夫维数等于它的高阶或低阶盒维数;

(2) 对于w∈R我们可以定义f的w次幂动压：

且Ψ的豪斯多夫维数等于P(w)的唯一零点。

计算结果见表1。

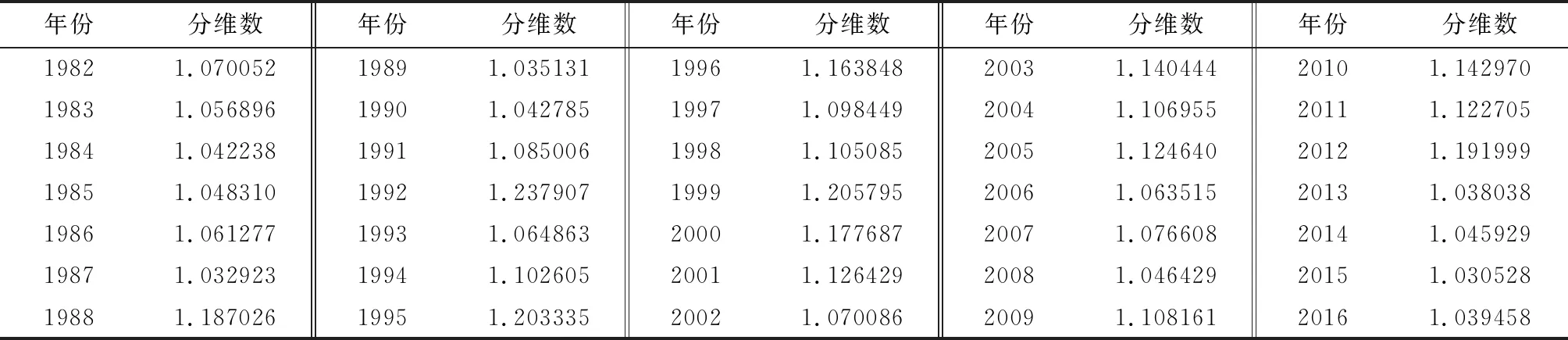
表1 张家山站年段径流过程分维数

2.2 降水不均匀指标的计算及耦合分析

对降水年内分配不均匀程度进行定量描述的研究有很多。近年来，有学者将不均匀系数、信息熵、集中度和集中期等指标单独或组合使用来开展不同地区降水年内分配特征的研究[16-17]，以下是对集中度和集中期的简要介绍。

将各月的降水量数值看作向量的长度，而对应的月份则当作向量的方向[18]，1月—12月的向量角度分别取 0°～330°，每月间隔30°，计算公式如下：

Rpc=arctan(Rxt/Ryt)

(2)

式中:Rti为第i月的降雨量；βi为第i个月的向量角度；Dpc为降水集中度；Rpc为降水集中期。当降水量平均分配在每个时段时，Dpc=0；当降水量集中于某一个时段时，降水集中度达到最大值，等于1。

经过综合分析，本文选用刘鑫[19]在辽宁省凌河流域降雨变化规律研究中使用的年内分配不均匀系数，计算公式如下：

(3)

由于降雨数据皆是来自于中科院水土保持研究所黄土高原生态环境数据中心，公布之前经过了严格的三性审查，故直接运用。为了表达流域内整体的降水年内分配情况，同时由于选用的三个气象站点环县、崆峒、长武在流域内分布均匀，故决定用三个站点降水不均匀系数的平均值作为整个流域的降水不均匀系数以代表实际情况。运用公式(3)计算得到流域1982年—2016年的年降水分配不均匀系数见表2。

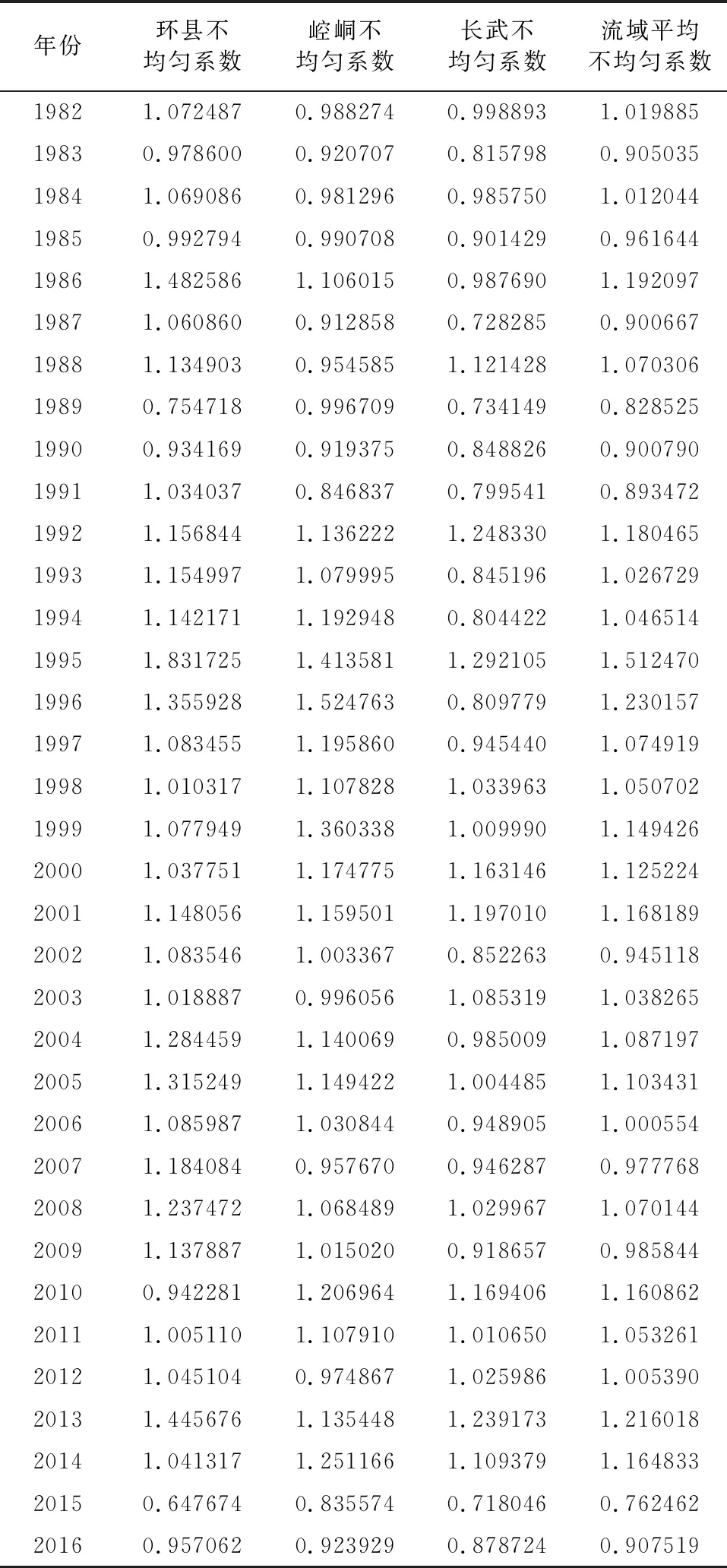
表2 年降水分配不均匀系数

可见流域内降水的年际间不均匀程度有明显的区别，这在一定程度上解释了径流过程年际间复杂程度的改变。进一步分析单一影响因子降水与径流过程分维数的关系，以降水不均匀系数为横坐标，相应的径流过程分维数为纵坐标，作相关分析见图1。

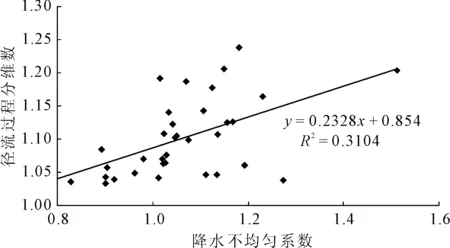
图1 分维数与降水不均匀系数关系图

分析图1，由拟合公式的系数为0.232 8可知，降水的年内分配情况确实对年径流过程的复杂程度产生了影响，且由相关系数为0.557 1知影响程度并不小。这与定性描述中提到的降水分配越不均匀，径流过程越复杂一致。

2.3 NDVI的计算及耦合分析

将获得的SPOT卫星的NDVI遥感图像导入Arc Map10.5，进行数据处理，得到了1982年—2016年泾河流域的年NDVI数据，见表3。

分析表3可知，流域内的归一化植被指数在年际间变化也较明显，进一步分析归一化植被指数表示的流域内植被的覆盖情况与径流过程分维数之间的定量关系见图2。

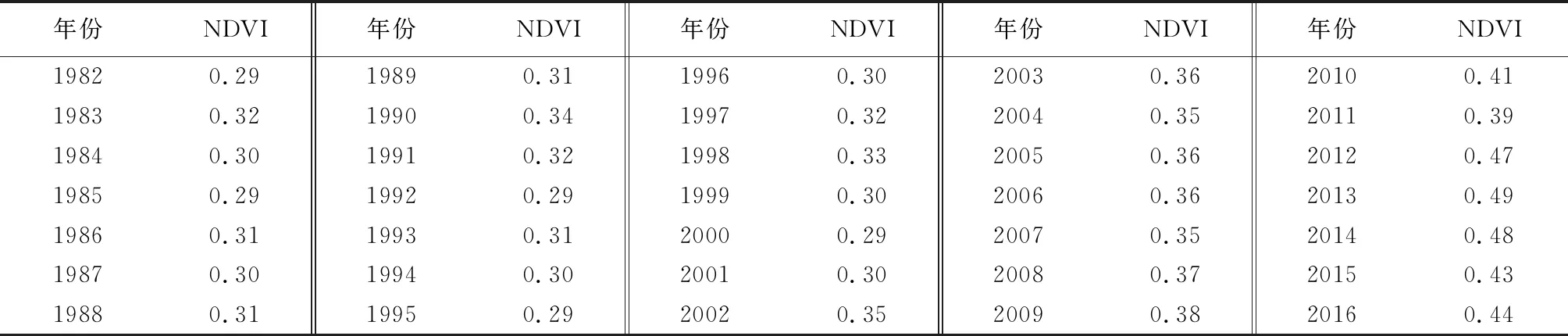
表3 泾河流域年NDVI系列

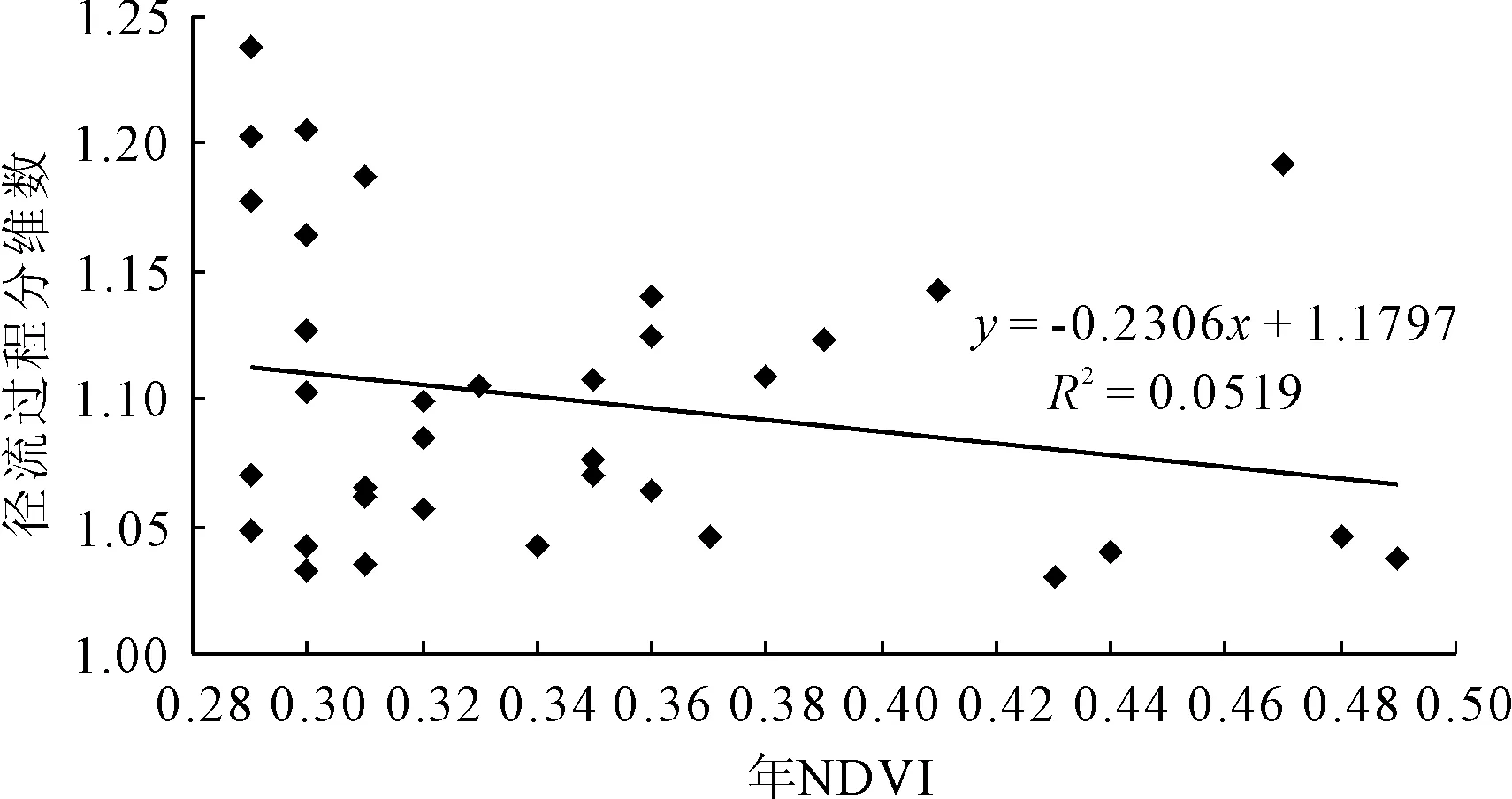
图2 分维数与年NDVI关系图

不难看出，图2与定性分析的情况是一致的。年NDVI代表的是流域的植被覆盖情况，年NDVI值越大，流域植被覆盖越好，年径流过程相对简单，径流分维数相对较小，所以是一种下降的趋势。同时，可以看到泾河流域年径流过程分维数与年NDVI的相关系数只有0.227 8，相关度不高，说明降雨对径流过程的影响较流域植被覆盖更大。

3 分维数与降水不均匀系数以及NDVI之间的定量关系及检验分析

3.1 定量关系的计算

对各结果采用平均值归一化的方法进行处理，可消除由于不同类型数值统一处理而产生的误差，结果见表4。

鉴于本论文之前所述，先假设泾河流域径流过程分维数与降水不均匀性指标、年NDVI之间存在线性关系，然后进行检验。其线性模型为：

(4)

式中：y为年径流过程分维数；x1为泾河流域降水不均匀系数；x2为该区域年NDVI；β0，β1，β2为回归系数；ε为相应于y的随机误差。

现根据1982年—2016年的35组数据(yi，x1i，x2i)，i=1,…,n；n=35，得：

(5)

记：

ε=[ε1…εn]T，β=[β0β1β2]T

所以，公式(5)可表示为：

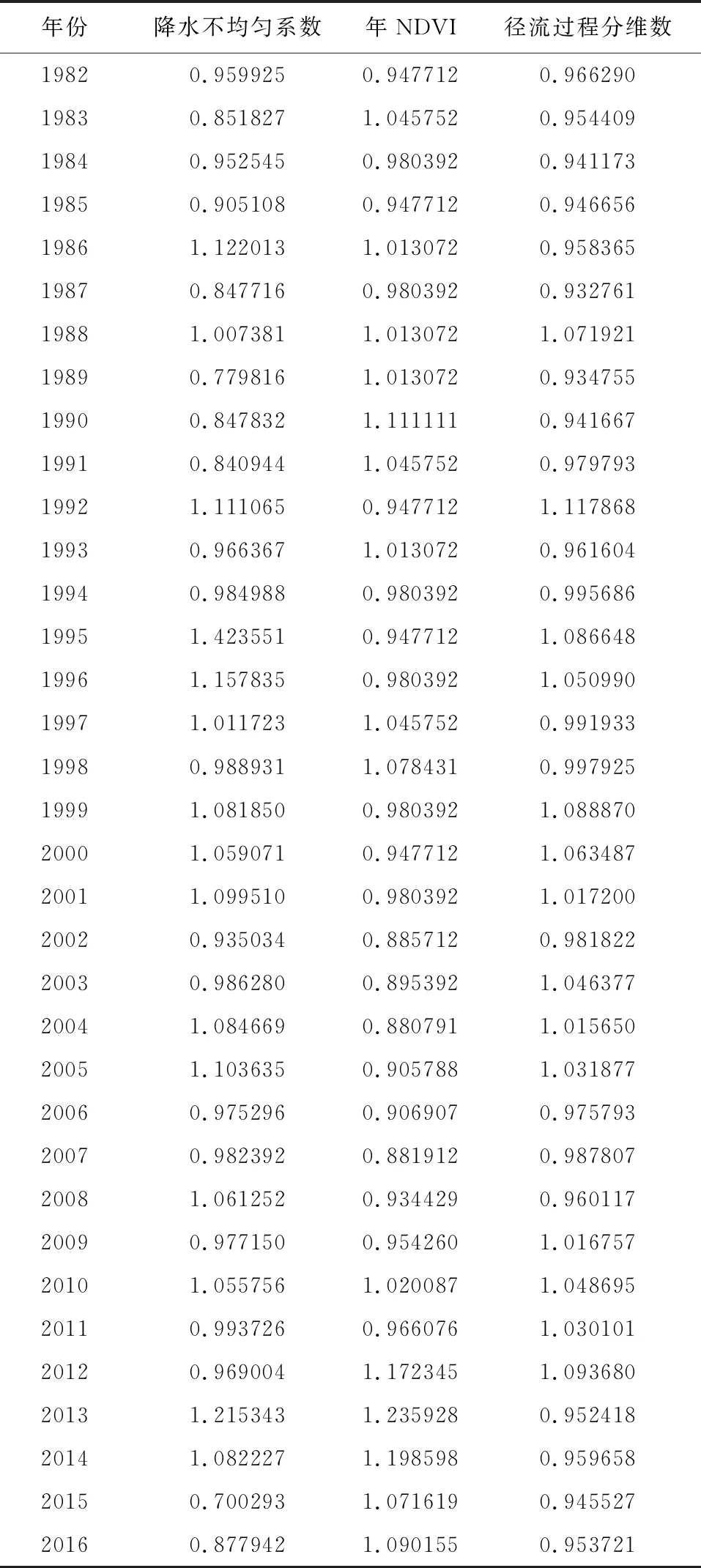
表4 各指标归一化结果

(6)

式中:En为n阶单位矩阵。

接下来对因变量y与自变量x1和x2之间的线性关系进行检验，作如下假设：

H0∶βj=0(j=0,1,2)

(7)

当H0成立时，有：

m=2

(8)

式中：U为回归平方和；Q为残差平方和。

在MATLAB中，使用“regress”命令对年径流过程分维数和降水不均匀系数、年NDVI进行线性拟合，用法为：

[b， bint，r， rint， stats]=regress(Y,X,α)

式中:Y为因变量矩阵;X为自变量矩阵;α为显著性水平(缺省时设定为0.05)；b，bint为回归系数估计值和置信区间；r，rint为残差(向量)及其置信区间，stats是用于检验估计模型的统计量，有四个数值，第一个是R2，第二个是F值，第三个是与F对应的概率p(α>p拒绝H0，模型成立)，第四个是残差的方差s2。计算结果见表5。

表5 MATLAB拟合结果表(显著性水平α为0.01)

当显著性水平α为0.01时，检验参数stats：第二项F为8.003 1，查F的上侧分位数F0.01(2,32)=5.336，F>F0.01(2,32)；第三项为0.001 5，有p<α=0.01，得到相关系数R为0.58的有效回归模型为：

y=0.8887+0.2129x1-0.1016x2

(9)

式中:y为归一化年径流过程分维数；x1为归一化年降水不均匀系数；x2为归一化年NDVI。

3.2 检验分析回归模型

分析所获得的残差，与原模型基本吻合。总体来说，多元线性回归模型不错，相关系数达到了0.58。比较用模型计算的泾河流域年径流过程分维数和原计算的年径流过程分维数见图3。

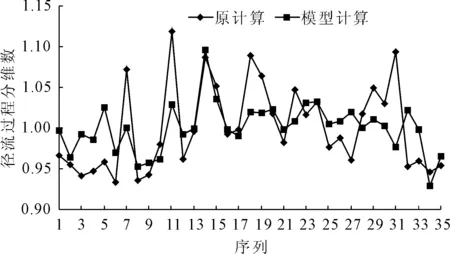
图3 回归模型效果图

观察上图，可知回归模型效果还不错，较好地与原计算序列符合。

分析多元线性回归模型(公式(9))可知，降水年内分配越不均匀，植被覆盖越小，分维数就越大，径流过程越复杂，这与研究过程中的定性描述是一致的。

4 结 论

本文利用泾河流域张家山水文站的月径流资料，环县、长武、崆峒气象站的日降雨数据以及SPOT卫星的NDVI遥感图像，以年为单位，分析了1982年—2016年泾河径流过程分维数与该流域降水不均匀系数、NDVI之间的关系。结果表明泾河流域径流过程分维数与该流域降水不均匀系数呈正相关，而与NDVI呈负相关。降水年内分配越不均匀，植被覆盖越小，径流过程越复杂，分维数也就越大，符合平常认知。另一方面，通过比较分维数与降水不均匀系数和分维数与NDVI的相关系数，分别为0.557 1和0.227 8，可知在泾河流域中降水对径流过程的影响较流域植被覆盖更大。