基于集对分析法的山岭隧道坍塌风险评价
茶增云,陈 舞,肖振江,王云龙,郭跃文
(1.西双版纳景海高速公路建设投资有限公司, 云南 景洪 666100;2.云南腊满高速公路有限公司, 云南 西双版纳 666300;3.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室, 湖北 武汉 430071;4.中国科学院大学, 北京 100049)
目前隧道正朝着大断面、扁平化趋势发展,三车道、四车道以上的大断面小净距和连拱隧道数量不断增多,导致工艺复杂、工法转换多,施工技术难度、坍塌风险日益增大。尤其是修建于崇山峻岭之中的山岭隧道,其施工条件的复杂性、地质条件的多样性、构造活动的强烈性和风险影响因素的不可预见性更加突出,进一步加大了坍塌事故的发生[1]。因此,准确评价山岭隧道施工中的坍塌风险具有重要现实意义。
目前,隧道坍塌风险评价方法有多种,如风险矩阵法[2]、层次分析法[3]、事故树法[4-6]、神经网络法[7]和模糊综合评价法[1,8]等。这些研究成果对隧道施工期坍塌风险分析均发挥了重要作用。然而受地形地貌、地质构造、勘察设计和施工等多种因素的影响,山岭隧道坍塌风险影响因素往往呈现出复杂性、模糊性和不确定性等特征,将以上方法用于山岭隧道坍塌风险评价具有一定的局限性。集对分析理论是由我国学者赵克勤[9]教授于1994年提出的,是一种用来处理多因素不确定问题的有效方法。目前,该理论已经广泛应用于边坡[10-11]、基坑[12-13]、公路隧道[14-15]等岩土工程领域中,并取得了丰富成果。因此,本文提出了基于集对分析理论的山岭隧道坍塌风险评价模型,并将其应用到景海高速公路宾房2号隧道中。评价结果与实际情况较吻合,为山岭隧道坍塌风险评价提供了一种新的研究思路。
1 集对分析理论
1.1 集对分析原理
集对分析(Set Pair Analysis,SPA)是用集对和联系度来研究系统的确定性和不确定性及其转化规律的系统分析技术,可以定量处理模糊、随机、不确定性问题。该理论实质是将研究对象作为一个确定-不确定系统,用“对立”、“同一”2个特征来描述确定性,用“差异”描述不确定性,从“同、异、反”三个方面来研究系统的确定性与不确定性之间关系。
1.2 联系度的定义
将具有一定联系均包含N个特征的2个集合A,B组成一个集对,可用联系度μ来表示集对H=(A,B)的辩证关系,如下:
(1)
式中:p为差异不确定系数,p∈[-1,1];q为对立度系数,q=-1;N为集对特征总数,N=S+F+L,S,F和L分别为同一特征数、差异特征数、对立特征数;a,b,c分别为同一度、差异度、对立度,且a+b+c=1。
式(1)称为一般联系度或三元联系度。然而,有些问题可能存在不止一种差异程度,例如轻度差异、中度差异及重度差异。因此,有必要将三元联系度扩展到多元联系度来反映各种差异程度。把公式(1)展开,可得到多元联系度μn,如下:
(2)
简写为:
μn=a+b1p1+b2p2+…+bn-2pn-2+cq
(3)
式中:p1,p2,…,pn-2为差异度系数;b1,b2,…,bn-2为差异度分量,代表差异程度的不同,例如轻度差异、中度差异、重度差异等;q为对立度系数,并且规定:a∈[0,1],bn-2∈[0,1],c∈[0,1],且a+b1+b2+…+bn-2+c=1,p∈[-1,1],q=-1。b1,b2,…,bn-2是对差异度b的进一步划分,更深入地展示差异度大小。在不计p1,p2,…,pn-2,q的值时,p1,p2,…,pn-2,q仅代表一种标记。
2 山岭隧道坍塌风险评价的集对分析模型
2.1 隧道坍塌风险评价指标体系的建立
隧道坍塌是一个典型的不确定性问题。它是隧道工程固有属性和外部施工因素相互作用的结果。隧道工程地质和水文地质条件复杂,呈现出复杂性、模糊性和不确定性等特征。常规方法在处理这种模糊不确定信息时遇到困难。实际工程中,隧道坍塌的影响因素很多,并且这些因素相互作用。但总体来说,影响隧道坍塌的主要因素有自然因素、地质因素、勘察设计因素和施工因素。参考已有的山岭隧道塌方影响因素统计分析结果[1, 8, 16-20],选取年降雨量、地形地貌、围岩级别、深度比(隧道埋深H0/隧道高度H)、地下水状况(隧道每10 m的进水量(L/min))、不良地质情况、地质勘察准确程度、初期支护刚度、开挖断面面积、开挖方法、施工技术水平和施工管理水平12项因素(分别用X1,X2,X3,X4,X5,X6,X7,X8,X9,X10,X11,X12表示)作为隧道坍塌风险评价指标。其中,地形地貌X2、围岩级别X3、不良地质情况X6、初期支护刚度X8、开挖方法X10、施工技术水平X11和施工管理水平X12为定性因素,分级标准用定性语言描述,计算分析时参照文献[21]采用半定量的方法进行量化取值,具体分级标准及赋值情况见表1。对年降雨量X1、深度比X4、地下水状况X5、地质勘察准确程度X7、开挖断面面积X9为定量指标,用实测值进行评价,分级标准见表2。根据隧道坍塌特征,将评判空间T={P1,P2,…,Pm}定义为{P1,P2,P3,P4,P5},即Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ五级,分别表示无坍塌风险、较低坍塌风险、中度坍塌风险、高坍塌风险和极高坍塌风险。

表1 隧道坍塌风险评价的定性指标分级标准

表2 隧道坍塌风险评价的定量指标分级标准
2.2 隧道坍塌风险评价的集对分析模型
2.2.1 坍塌风险评价的五元联系度
针对坍塌风险评价问题,将评价指标与风险等级标准相结合,建立了集对。同时,将第I级等级标准作为参考标准,则评价指标在I级标准内的定义为同一度,Ⅱ、Ⅲ、Ⅳ级标准内的分别定义为差异偏同度、差异度、差异偏反度,Ⅴ级标准内的定义为对立度,根据式(2)及式(3),可将隧道坍塌风险评价的五元联系度μ5定义为:
b2p2+b3p3+cq
(4)
其中,N为坍塌风险评价指标总数。S为符合Ⅰ级标准的评价指标个数;F1为符合Ⅱ级标准的评价指标个数;F2为符合Ⅲ级标准的评价指标个数;L为符合Ⅴ标准的评价指标个数;另外,a=S/N,b1=F1/N,b2=F2/N,b3=F3/N,c=L/N。a,b1,b2,b3,c∈[0,1],并且a+b1+b2+b3+c=1。
2.2.2 评价指标等级联系度的建立
将山岭隧道坍塌风险评价指标划分为两类指标[10]:效益型指标和成本型指标。对于效益型指标,隧道坍塌风险等级随着评价指标取值的增大而降低,即越大越优。对于成本型指标,隧道坍塌风险等级随着评价指标取值的增加而增加,即越小越优。如表1和表2所示,在坍塌风险评价指标体系中,深度比X4、地质勘察准确程度X7属于效益型指标;其余指标均包括年降雨量X1、地形地貌X2、围岩级别X3、地下水状况X5、不良地质情况X6、初期支护刚度X8、开挖断面面积X9、开挖方法X10、施工技术水平X11、施工管理水平X12等都属于成本型指标。各评价指标对坍塌风险的影响由等级联系度反映,具体计算公式如下:
(1) 当评价指标为定性指标时,评价指标Xl的等级关联度为:
① 效益型指标(越大越优型):
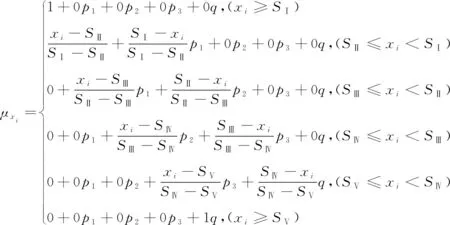
(5)
其中,SⅠ、SⅡ、SⅢ、SⅣ和SⅤ分别为评价指标的第Ⅰ—Ⅴ级标准临界值,且SⅠ≥SⅡ≥SⅢ≥SⅣ≥SⅤ。
②成本型指标(越小越优型):
(6)
其中,SⅠ≤SⅡ≤SⅢ≤SⅣ≤SⅤ。
(2)当评价指标为定量指标时,评价指标xi的等级关联度为:
①效益型指标(越大越优型):
(7)
其中,SⅠ≥SⅡ≥SⅢ≥SⅣ≥SⅤ。
②成本型指标(越小越优型):
(8)
其中,SⅠ≤SⅡ≤SⅢ≤SⅣ≤SⅤ。
2.2.3 综合联系度的确定
采用综合联系度来综合各评价指标对隧道坍塌风险等级的影响,计算公式如下:
(9)
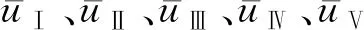
2.2.4 隧道坍塌风险等级的确定
(10)
(11)
2.2.5 风险评估流程
采用基于集对分析法进行山岭隧道坍塌风险评价技术线路如图1所示,具体步骤为:
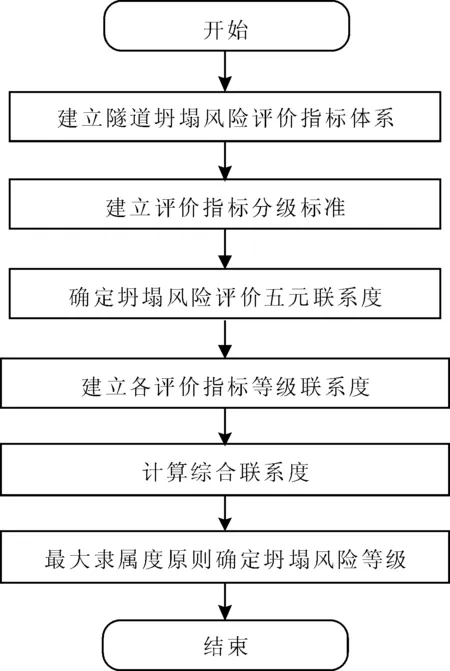
图1 基于集对分析法的隧道坍塌风险评价流程
(1) 建立了隧道坍塌风险评价指标体系和风险等级标准;
(2) 根据式(4)建立隧道坍塌风险评价的五元联系度;
(3) 利用式(5)—式(8)确定各评价指标的等级联系度;
(4) 采用式(9)计算得到综合联系度;
(5) 根据式(10)计算隧道坍塌风险联系度的同一度,差异偏同度、差异度、差异偏反度及对立度;并根据最大隶属度原则式(11)确定隧道坍塌风险等级。
3 工程应用
3.1 工程概况
为验证本文所提方法的有效性和准确性,以景海高速公路宾房2号隧道为研究对象进行坍塌风险分析。宾房2号隧道为分离式长隧道,左幅长度为2 218 m,设计最大埋深为118 m;右幅长度为2 230 m,设计最大埋深为113 m。隧道区海拔高程介于1 023 m~1 173 m之间,相对高差约150 m,地形起伏较大,变化较复杂,属中浅切割低山地貌区。隧道出口端K31+580—K31+530浅埋段下穿越全风化花岗岩层,左、右幅围岩均为Ⅴ级。该段隧道洞顶埋深为14.3 m~31.5 m,且隧道上方有一常流水冲沟,围岩富水且水源补给充分,岩体力学性质劣化严重,开挖扰动后极易发生围岩失稳。由于埋深较浅,围岩变形可能延伸至地表,造成地表沉陷、甚至冒顶事故的发生;另一方面,隧道结构受到的地形偏压影响大,支护结构受力不对称,可能造成支护结构局部破坏、失效。因此,本文所选该段右幅隧道K31+580—K31+530浅埋段进行坍塌风险分析。该处地质纵断面图如图2所示。
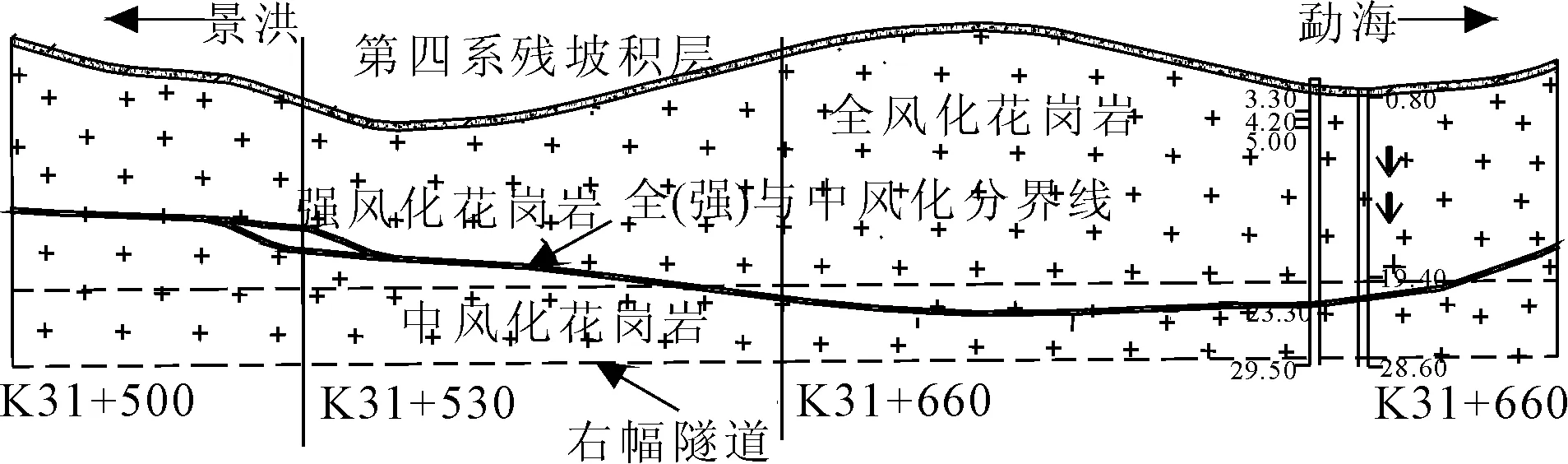
图2 右幅隧道K31+580—K31+530浅埋段地质纵断面图
通过对该段的工程地质、水文地质、掌子面及地质雷达探测成果的综合分析,并结合现场施工组织设计情况,可得里程K31+580—K31+530处各影响因素参数和等级,见表3。

表3 隧道坍塌风险因素参数
3.2 坍塌风险评估
基于集对分析法,对宾房2号隧道K31+580—K31+530段坍塌风险水平进行了研究。首先,根据表3得到符合I级标准的评价指标个数为0个;符合Ⅱ级标准的评价指标个数为1个;符合Ⅲ级标准的评价指标个数为3个;符合Ⅳ级标准的评价指标个数为3个;符合Ⅴ级标准的评价指标为5个。因此,a=0,b1=1/12,b2=3/12,b3=3/12,c=5/12,并且隧道坍塌风险评价的五元联系度 可以表示为:
(12)
其次,根据式(5)—式(8),建立了各评价指标等级联系度函数,如图3所示。结合表3中各评价指标的参数,计算得到各评价指标等级联系度,如下所示:
μx1=0+0p1+0p2+0p3+1q
μx2=0+0p1+1p2+0p3+0q
μx3=0+0p1+0p2+0p3+1q
μx4=0+0p1+0p2+0p3+1q
μx6=0+0p1+0p2+0p3+1q
(13)
μx8=0+0p1+1p2+0p3+0q
μx10=0+0p1+0p2+1p3+0q
μx11=0+0p1+1p2+0p3+0q
μx12=0+0p1+0p2+0p3+1q
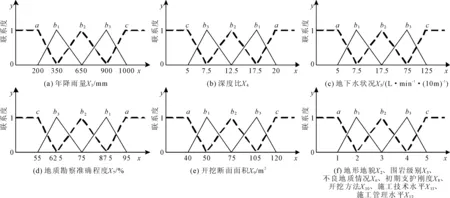
图3 各评价指标等级联系度函数
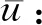
0.18p3+0.4834q
(14)
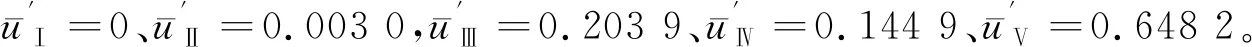
3.3 结果分析与验证
事实上,隧道在穿越K31+580—K31+530段时洞内发生了坍塌,并造成了地表塌陷,如图4和图5所示。分析其原因主要是:① 富水全风化花岗岩岩体较软弱,围岩自稳能力极差,流塑性强,施工扰动作用下围岩液化现象明显,围岩稳定性进一步变差;② 开挖方法选取不合理,循环进尺过大;③ 超前支护设计不合理;④ 监控量测开展不及时等。
3.4 优化施工组织设计
在吸取现场坍塌事故经验教训后,施工决策者将开挖方法由原来的二台阶法调整为三台阶预留核心土,并且循环进尺由原来的2 m调整为0.5 m。对地表浅埋段采用单根长9 m的Φ108*6 mm钢花管进行地表注浆加固,并且原设计双层小导管的超前支护,调整为Φ108×6 mm大管棚+Φ42×4 mm小导管联合超前支护,管棚每循环长度为20 m、搭接4 m,小导管每循环长度为4.5 m,搭接 2.5 m。同时,I18型钢钢架支护调整为I20b,间距为50 cm。此外,加强了洞内监测频率与现场施工组织管理等保证了右幅地表浅埋段顺利穿越。
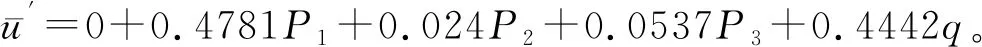
综上可知,基于集对分析法的评价结果与实际情况较吻合,说明将该理论用于山岭隧道坍塌风险评价中是合理可行的。

图4 宾房2号隧道右幅K31+565.5隧道坍塌状况

图5 K31+565.5地表塌陷坑
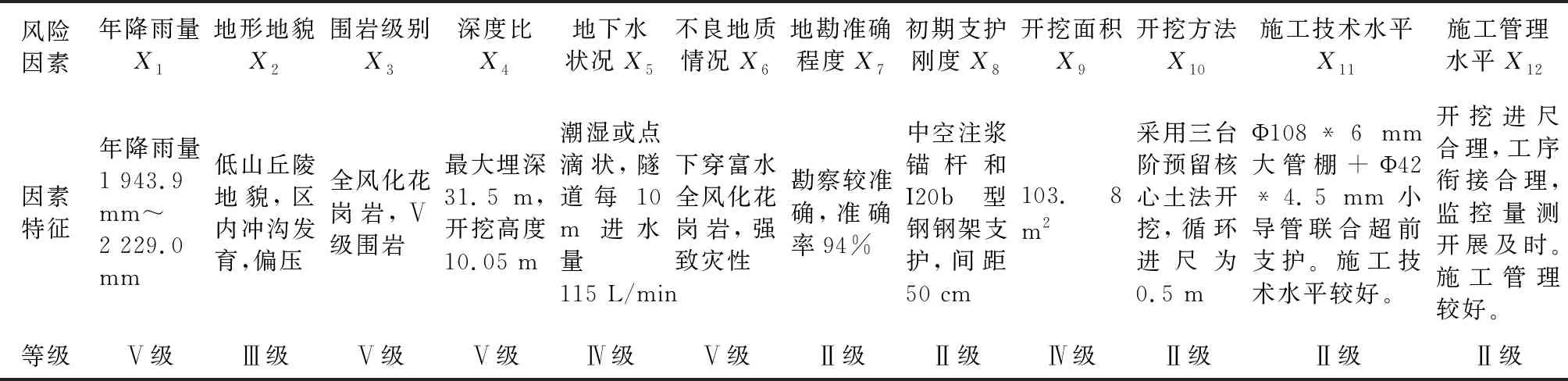
表4 调整后隧道坍塌风险因素参数
4 结 论
(1) 将评价指标与风险等级标准相结合,并将风险评价指标分为效益型指标和成本型指标两大类,基于集对分析法,建立了评价指标的等级联系度,量化了评价指标与风险等级的集对联系度。
(2) 将集对分析理论应用到山岭隧道坍塌风险分析中,并建立了隧道坍塌风险评价的集对分析模型。利用最大隶属度准则来判别隧道坍塌风险等级,较好的解决了山岭隧道坍塌风险等级评价中多指标性、模糊性和不确定性等问题。
(3) 将本文方法应用到宾房2号隧道中,评价结果与实际情况较吻合,为山岭隧道坍塌风险评价提供新思路。

