基于分布状态估计的低频减载策略

刘健超，高 键，程 驰

（1.江苏科技大学 电子信息学院，江苏 镇江 212003；2.国网江西省景德镇市电力公司，江西 景德镇 333000）

0 引 言

当前电力推进系统已在舰船上得到广泛应用，相对于机械直接推进系统，其有机动性好和振动噪声小等优点,但会导致舰船的用电量大幅提升。相较于陆上电网，舰船电网的容量较小，面对的环境较恶劣，发电机突然投入或负荷激增会导致舰船电力系统的频率发生振荡，因此将低频减载方案引入舰船电站中具有重要意义。

目前，低频减载技术已在孤岛电站上得到广泛应用。例如：文献[2]提出一种将潮流算法与动能定理相结合的方法，分析出对舰船电力系统的瞬时频率影响较大的负荷，从而进行精准切除；文献[3]提出一种考虑调速器的交直流系统减载控制策略，分阶段进行负荷的切除和恢复；文献[4]利用广域监测系统（Wide Area Monitoring System, WAMS）对系统频率和频率变化率进行监测，由此构建节点的减载贡献因子，从而更好地恢复系统频率。然而，目前大多数减载控制策略都是根据一定的频率阈值，以预先确定的延时断开一定量预定义的负荷或馈线。这种预定义减载方法的主要缺陷是现有的常规潮流算法由于离线潮流本身的许多原始数据都是一些粗略数据，与实时运行状态存在一定的差异，在实际操作中会因欠切或过切现象而产生恶劣后果。

虽然目前在舰船领域对低频减载技术的研究相对较少，但舰船电力推进系统与孤岛电站有很多相似之处。本文借鉴孤岛电站上的低频减载控制策略，通过计算舰船电力推进系统各条总线的功率缺额，对舰船电站低频减载控制策略进行研究。该方法采用加权最小二乘算法求解出电力推进系统中每条总线的功率缺额，同时按负载程度及其重要性赋予不同的权值，据此通过最小化误差相量求取电力推进系统状态的最优估计。此外，优化减载量，使本文所述方法减载更精确，更有利于保证舰船电力推进系统的稳定性。

1 电力推进系统

1.1 电力推进系统概述

电力推进系统是舰船电站的核心系统之一，主要由发电子系统、储能子系统、负载管理系统、推进子系统、配电子系统和电力变换装置等6 部分组成（见图1）。在舰船航行期间，舰船电站是一个孤立的电力系统，船上各系统的能量都来源于此。舰船上的发电机组发生故障和负载突变会影响舰船电力推进系统各条总线的频率波动。因此，电力推进系统的首要任务是保证舰船电站安全、稳定、连续运行。

1.2 等效惯性中心频率

为保持舰船电力推进系统稳定运行，必须精确控制船上发电机的运行速度，因为许多发电机辅助设备的性能都与频率有关，若这些设备性能不佳，可能会降低电站的输出功率或引起发电机跳闸。因此，在发电机中，通常为原动机配备一个调速器，用以监测轴的转速，若轴的转速低于（高于）基准转速，则减小（增加）施加在轴上的扭矩。调速器通过在一次扰动之后提供一次调整来限制频率偏差，不将频率返回到其标称值。若要使系统频率恢复到标称值，需进行二次调整。低频减载是将标称频率以下的频率偏差限制在可接受的范围内，防止发电机跳闸的有效措施。因此，协调发电机的低频保护与低频减载十分重要，若要避免系统崩溃，必须在实施发电机低频保护之前进行减载。

本文对系统频率和频率变化率进行实时监测，通过同步测量值计算舰船电网的等效惯性中心频率。将减载分为4 个阶段，对等效惯性中心频率的阈值进行触发，试验采用的阈值分别是59.5Hz、59.0Hz、58.5Hz 和58.0Hz。同时，监测频率变化率，若d f /d t＜ 0持续100ms 且惯性中心频率 f ＜ 59.5 Hz ，则执行第一阶段。等效惯性中心频率通过多次测量，根据测量值进行计算，其表达式为

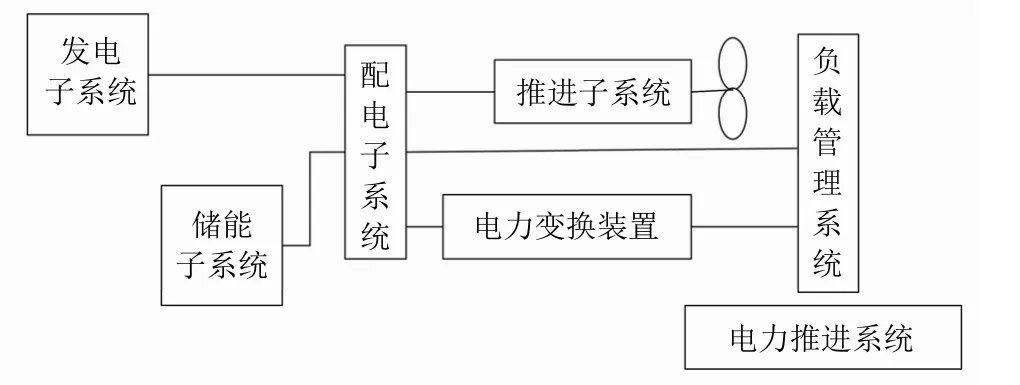
图1 舰船电力推进系统

式(1)中： f为等效惯性中心频率； f为第i 次测量的系统频率；H为惯性时间常数。当单台发电机发生局部或区域间振荡时，计算等效惯性中心频率是测量系统频率的有效手段。通过不断地监测频率和频率变化率，使得故障发生时负载管理系统能立即动作，按优先级对负荷进行切除。

2 分布状态估计算法

配电子系统是电力推进系统的主要构成部分之一，本文在配电子系统中加入伪测量设备，使其由实时测量设备和伪测量设备组成。实时测量设备主要安装在主变电站中；伪测量设备由实用程序，通过算法提高系统各量测量的精度。相比常规潮流算法，分布状态估计算法的优势在于其能利用冗余度提高数据的精确度，通过测量增加量得到更精确的结果。本文采用加权最小二乘算法求解分布状态估计量。加权最小二乘算法通过权值保证更精确的测量值在估计过程中更重要，即其权值更大。

分布状态估计量Z的测量向量为

通过迭代求解(5)得到状态向量x。

式(5)中： H( x)为非线性函数 h( x )的雅可比矩阵； G ( x)为增益矩阵。 G ( x)的计算式可表示为

本文所述分布状态估计算法通过最小化误差向量求得电力系统状态的最优估计，分布状态估计量的测量矩阵由多种测量方法组成，如线路功率流、母线功率注入、母线电压大小和线路电流。然而，在构建测量矩阵时，需将实时测量与伪测量相结合。在该方法中，采用伪度量方法提高分布状态估计量的收敛性。采用伪度量方法解决 h( x) 的稀疏性问题。

求解出总线i 上的有功功率P 和无功功率Q，有

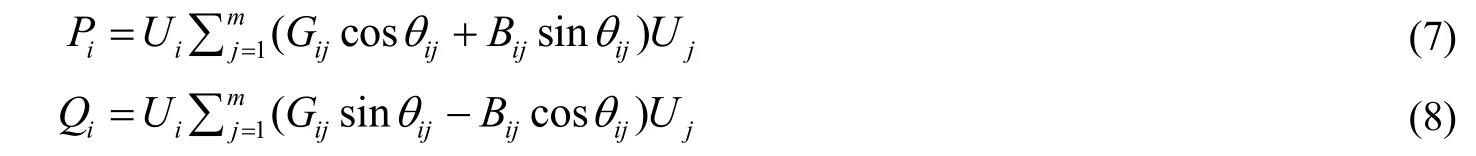
式(7)和式(8)中： G为总线i 与总线j 之间的电导； B为总线i 与总线j 之间的电纳；U和U分别为总线i和总线j 的电压； θ为总线i 与总线j 之间的相位角。

同时，求解出总线i 与总线j 之间的有功潮流方程 P和无功潮流方程 Q，有

式(9)和式(10)中：G为线路i 的电纳；B为线路i 的电导。

本文所述分布状态估计流程图见图2，其中每条总线上的功耗是通过负载模型、新的电压和角度的计算值更新的。最后，将每条总线上的功耗发送给负载管理系统，确保按优先级精准减载。

图2 基于加权最小二乘法的分布状态估计流程图

3 改进减载量的策略

负载管理系统负责估计电力推进系统中的功率不平衡。当扰动发生时，电力系统中有n 台发电机，其中第i 台发电机的转子的运动方程为

式(11)中： i = 1,2,...,n； δ为第i 台发电机的功角；t 为时间； Δω为第i 台发电机的角速度偏移值；H为惯性时间常数；ω为额定角速度；ω为角速度的标幺值； P为第i 台发电机的机械功率； P为第i 台发电机的电磁功率。功率均采用标幺值，基准值为100MW。

通过使式(11)两端同时乘以 ω，并进行相应的变换，同时在时间 [ t, t]上对左右两边进行积分，可得到系统在时间 t到 t的有功缺额为

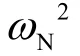
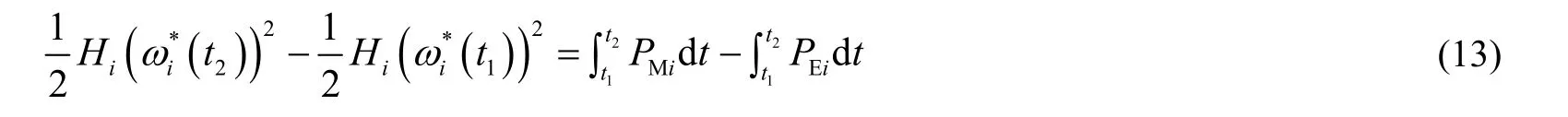
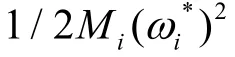
考虑到扰动初始时刻电力推进系统中电压的变化程度远大于频率的变化程度，结合系统中负荷节点电压变化对负荷有功功率调节系数的影响，得到修正后的有功不平衡 ΔP 的计算式为

式(15)中： P为系统稳态时，节点q 处负荷消耗的有功功率； P为系统受到扰动的瞬间，节点q 处的有功功率。

最后负载管理系统根据系统总体有功不平衡值，按负载的重要程度估算出每条总线应切除的负荷量，由此进行减载，本文分4 个阶段进行减载，各阶段的不平衡率分别为70%、15%、10%和5%。同时，考虑旋转备用容量和发电机的调速器。

4 仿真分析

本文通过Matlab/Simulink 对舰船电力推进系统进行仿真，仿真系统为IEEE（Institute of Electrical and Electronics Engineers） 3 机9 节点系统。每台发电机的电制为6.6kV/60Hz，装机容量为1MW，基准值为100MW。仿真时假设负载1 为一级负荷，负载2 和负载3 为二级负荷，负载4～负荷6 为三级负荷。同时，通过2 个测试验证本文所采用方案的有效性：

1) 1 号同步发电机在 t=10 s时发生故障。图3 为本文方法下发电机故障频率变化曲线。由图3 可知：在 t=10 s时，由于1 号同步发电机发生故障，系统惯性中心频率迅速下降；在 t= 10.4 s 时，负载管理系统迅速做出反应，第一阶段切断应切负载的70%，此时舰船电力系统的频率继续下降；在 t= 10.8 s 时，舰船电力系统的频率进一步下降到58.9Hz，负载管理系统迅速进行第二阶段动作，第二阶段切断应切负载的15%，此时舰船电力系统的频率迅速回升。系统惯性中心频率存在一个阶跃，在 t=21s时恢复到初始频率。

2) 1号同步发电机在t=10s时，负荷突然增大10%。图4为本文方法下负荷突增频率变化曲线。由图4 可知：在 t=10 s时，由于负荷突增，系统惯性中心频率下降；在 t= 11.2 s 时，负载管理系统迅速做出反应，此时舰船电力系统的系统频率回升。系统惯性中心频率存在一个阶跃，在 t=19 s时恢复到初始频率。

图3 本文方法下发电机故障频率变化曲线

图4 本文方法下负荷突增频率变化曲线

3) 本文采用的减载控制策略通过设置的分布状态估计控制器对系统基本轮进行控制，实时测量设备监测主变电站的电压幅值与相角和系统频率的变化情况，执行伪测量设备（即分布状态估计控制器）的流程图如图2 所示。采用迭代法不断更新系统电压的幅值和相角，寻找每条总线有功功率的最优解，从而更加精确地计算出系统有功缺额。同时，利用通信设备将计算出的有功缺额传输到负载管理控制器中，按有功缺额和优先级切除相应负载。此外，结合上述2 个测试将本文采用的方法与已有的低频减载策略相对比，结果见图5。由图5 可知：当发电机发生故障时，采用本文所述方法之后，频率振荡幅度更加平稳，即切除负荷更加精确，系统最低频率为58.9Hz 时减载器即发生动作，而采用已有的控制策略在系统频率低于57.5Hz 时才发生动作；同时，采用本文方法，系统反应时间更短，故障发生之后 t= 10.4 s 减载装置即发生动作，而采用已有的控制策略在 t= 10.6 s 时减载装置才开始动作，且恢复为安全频率的时间较长。图6 为负载突增下本文方法与已有控制策略的频率变化对比。由图6 可知，当负载突增时，本文所述方法同样具有良好的作用。

图5 发电机故障下本文方法与已有控制策略频率变化对比

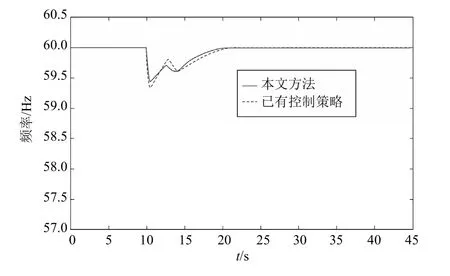
图6 负载突增下本文方法与已有控制策略频率变化对比

5 结 语

本文基于状态估计算法和发电机运动方程提出了一种新的减载控制策略，通过该策略可分析每条总线的负载需求。同时，提出了一种更精确的切负荷策略，并在IEEE 3 机9 节点系统中进行了仿真。此外，对本文所述方法与已有减载控制策略进行了对比，本文所述方法在优化减载量的同时考虑了负荷的优先级。仿真结果表明，本文所述方法不仅能使减载量更精确，而且能缩短频率恢复时间。

本文采用伪测量的方法减少了舰船电力推进系统对大规模部署实时测量设备的依赖，使得舰船整体的经济性得到了提升。同时，通过优化减载量有效减少了过度切除负荷的现象，降低了过度切除负荷造成的影响，使得舰船电力推进系统的稳定性有所提升。综上所述，本文所述方法能较好地适应舰船电力推进系统。