一个中考常考结论的探究
王锋

一、结论引入
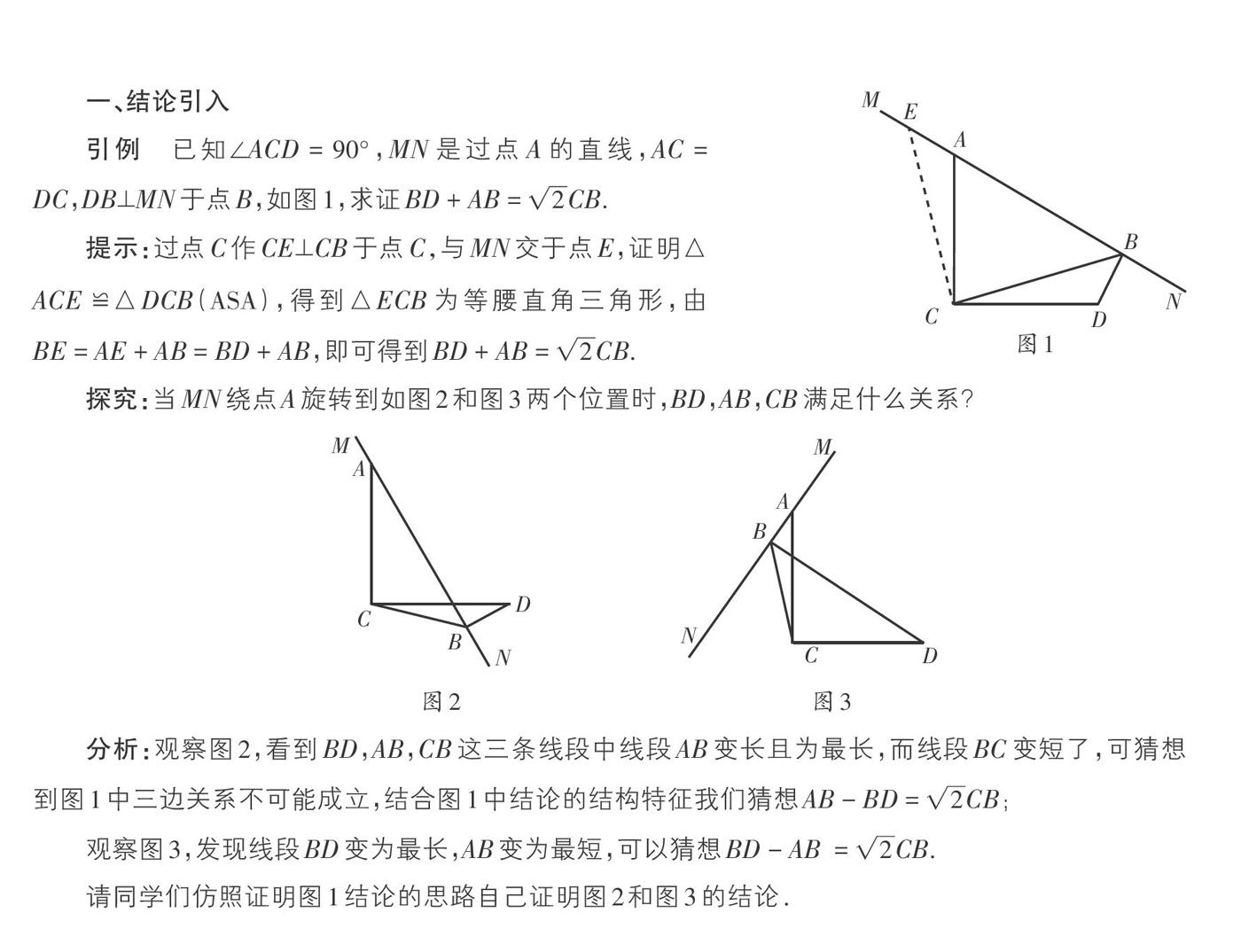
引例 已知∠ACD = 90°,MN是过点A的直线,AC = DC,DB⊥MN于点B,如图1,求证BD + AB = [2]CB.
提示:过点C作CE⊥CB于点C,与MN交于点E,证明△ACE ≌△DCB(ASA),得到△ECB为等腰直角三角形,由BE = AE + AB = BD + AB,即可得到BD + AB = [2]CB.
探究:当MN绕点A旋转到如图2和图3两个位置时,BD,AB,CB满足什么关系?
分析:观察图2,看到BD,AB,CB这三条线段中线段AB变长且为最长,而线段BC变短了,可猜想到图1中三边关系不可能成立,结合图1中结论的结构特征我们猜想AB - BD = [2]CB;
观察图3,发现线段BD变为最长,AB变为最短,可以猜想BD - AB = [2]CB.
请同学们仿照证明图1结论的思路自己证明图2和图3的结论.
反思:处理此类问题的突破口,一般是先构造出表示某线段[2]倍或[3]倍的线段,这时要以常见的特殊三角形为模型,如:等腰直角三角形的斜边是直角边的[2]倍;顶角为120°的等腰三角形的底边长是腰长的[3]倍;含30°角的直角三角形中,较长的直角边等于较短直角边的[3]倍;等等. 然后利用全等三角形进行线段之间的等量代换,最终获得问题的结论.
二、实战演练
例(2020·辽宁·本溪)如图4,射线AB和射线CB相交于点B,∠ABC = α(0°<α<180°),且AB = CB.D是射线CB上的动点(点D不与点C和点B重合),作射线AD,并在射线AD上取一点E,使∠AEC = α,連接CE,BE. 如图4,当点D在线段CB上,α = 120°时,请写出线段AE,BE,CE之间的数量关系,并说明理由.
分析:从图形中可以发现线段AE最长,于是,如图5,在AE上截取AF = CE,连接BF,过点B作BH⊥EF于H,证△ABF ≌△CBE(SAS),得出∠ABF = ∠CBE,BF = BE,由等腰三角形的性质得出FH = EH,根据“30°角所对的直角边等于斜边的一半”及勾股定理容易得出FH = EH [=32]BE,进而得出结论.
解: AE [=3]BE + CE,理由如下:
如图5,在AD上截取AF = CE,连接BF,过点B作BH⊥EF于H,
∵∠ABC = ∠AEC,∠ADB = ∠CDE,
∴∠A = ∠C,
在△ABF和△CBE中,[ AF=CE, ∠A=∠C, AB=CB,]
∴△ABF ≌ △CBE(SAS),
∴∠ABF = ∠CBE,BF = BE,
∴∠ABF + ∠FBD = ∠CBE + ∠FBD,∴∠ABC = ∠FBE,
∵∠ABC = 120°,∴∠FBE = 120°,
∵BF = BE,
∴∠BFE = ∠BEF [=12×](180° - ∠FBE)[=12×](180° - 120°) = 30°,
∵BH⊥EF,
∴∠BHE = 90°,FH = EH,
在Rt△BHE中,EH [=32]BE,
∴EF = 2EH = 2 [× 32]BE[ =3]BE,
∵AE = EF + AF,AF = CE,
∴AE[ =3]BE + CE.
点评:添加适当的辅助线构造全等三角形是解决问题的难点与关键.

