液动无控型单向阀关闭特性CFD分析*
李 莎
(上海电机学院,上海 200240)
0 引言
单向球阀是液压系统中较为常见的一类阀,通常根据球阀开闭有无控制分为主动控制式和自由落位式。自由落位式单向球阀由油道和小球组成,小球在重力或者液体的作用下完成落位,实现流动的通断控制。自由落位式球阀结构紧凑、流通阻力小、密封性能好、加工维修成本低廉,在汽车、工程机械、航空和船舶等行业的液压控制系统中使用广泛。但是自由落位球阀缺少控制元件,球阀开启和关闭时,流体处于高度非线性非定常流动,流体与小球的相互作用力在时刻变化,导致球阀的开闭特性极为复杂,增加了工程应用的难度。目前国内外学者通过理论、实验和CFD方法研究了主动控制式球阀开闭时的流场特性、阻力特性、流量系数、汽蚀、小球偏置影响等问题,而对于自由落位式球阀相关研究的文献较少。
本文以自由落位式球阀为研究对象,基于CFD动网格方法模拟小球瞬态落位过程,着重研究小球落位过程中的受力机理、球阀关闭响应特性和落位速度等问题,为理论研究和性能评估提供一种仿真计算方法。
1 物理模型建立
1.1 球阀力学模型
本文研究对象是水平方向开闭的一类梭阀,模型包括三个流通口A、B、C和2个小球B1、B2,如图1所示。该阀随三个流通口的状态变化可以实现三种通断状态:当A口作为进口时,液体流动产生的液压力推动小球B1打开,同时液体推动小球B2关闭,实现AC导通模式;当进口切换为B口时,同理液压力推动小球B2打开,B1关闭,实现BC导通模式;当C口作为进口时,两个小球均处于关闭状态,整个阀处于关断状态。考虑实际应用中小球质轻且光滑,可以忽略小球与油道壁面的摩擦力f。单向球阀关闭时,小球主要受表面液体压力Fp、液体剪切力Fτ、重力Fg以及相应的力矩Tp、Tτ和Tg,如图2所示。小球受到的作用力和力矩离散后的公式如下:

图1 球阀油道通断示意图
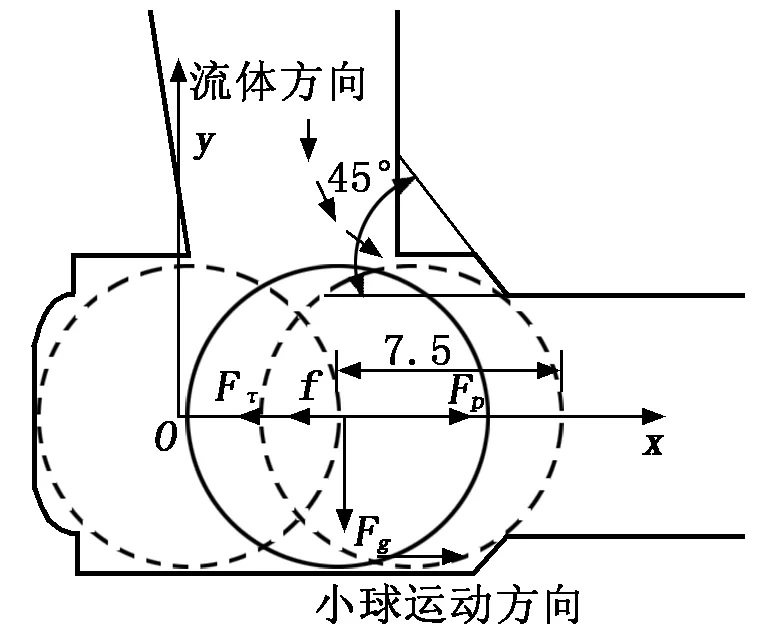
图2 小球受力分析示意图
Fp=∑surfpsurfasurf.
(1)
Tp=∑surf[rsurf×(psurfasurf)].
(2)
Fτ=-∑surfτsurfasurf.
(3)
Tτ=-∑f[rsurf×(τsurfasurf)].
(4)
F=∑surfpsurfasurf-∑surfτsurfasurf.
(5)
T=∑surf[rsurf×(psurfasurf)]-∑surf[rsurf×(τsurfasurf)].
(6)
其中:surf为小球表面离散后的微元面;psurf为压力;asurf为面的矢量;rsurf为力矩矢量;τsurf为剪切力矢量;F为小球水平方向所受合力;T为小球所受合力矩。
1.2 动网格理论
动网格理论在旋转机械、发动机进排气以及船舶行业CFD分析中应用十分广泛,其中主要的实现方法有旋转坐标系法、网格变形重构法、多套网格替换法以及嵌套网格法等等。根据动网格适用环境,本文采用嵌套网格方法。嵌套动网格需要静态环境网格和动态小球网格,前者为油道流体网格,后者为小球网格。
通过初始化将小球网格嵌入油道网格,内部保留小球的边界,外部保留油道的边界,形成完整的计算模型,如图3和图4所示。计算过程中,第n时间步计算结束后,小球网格按照计算结果移动vt距离,移动后的小球网格与油道网格重新嵌套得到第n+1个时间步的网格,从而实现了固液之间相互作用和小球运动的物理模型。

图3 嵌套前网格
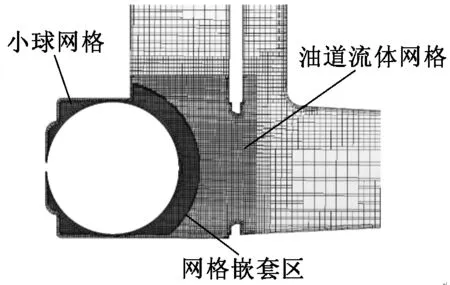
图4 嵌套后网格
1.3 边界条件和计算工况
本文研究AC导通、小球B2关闭的过程,仿真模型中将A口设为流量进口,B口和C口均采用压力出口边界,初始状态两个小球均处于开启状态,小球和油道设置为刚体无滑移壁面,考虑壁面边界层效应和壁面流体剪切力与小球的相互作用。油道壁面和小球之间间隙极小,只保留小球在油道方向的平动和三个方向的转动,忽略小球在另外两个方向的平动。初始状态下,球阀完全打开,小球速度为0 m/s,以此时小球质心作为坐标系原点,建立的坐标系如图2所示,z轴由右手法则确定。
本文分别计算了油道流量和小球质量对球阀关闭时间、落位速度的影响,得出不同设计参数和球阀性能之间的关系,具体仿真方案如表1所示。其中小球直径Φ=12 mm,质量m=3.5 g。进口A流量Q=16 L/min,小球B2落位行程L=7.5 mm,小球落位喉口倒角为45°。
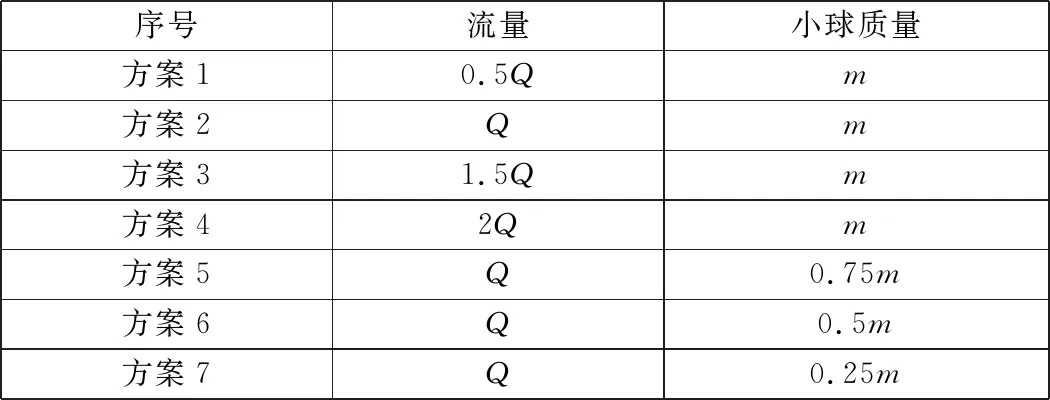
表1 仿真计算方案
2 仿真结果分析
2.1 球阀受力研究
采用方案2作为研究对象,模拟了小球置于X=0 mm、X=-2 mm和X=-4 mm三个位置时的受力情况,计算结果见表2。研究发现:①在三个位置小球所受的静压力大于剪切力,由于球阀喉口和小球的节流效果,部分静压转化为动压,从而在喉口位置静压力降低,小球在表面压差作用下开始慢慢向喉口移动;②小球从X=0 mm移动到X=-2 mm所受静压力只增加了8.8%,从X=-2 mm移动到X=-4 mm所受静压力增加了122%。小球在不同位置的静压力云图如图5~图7所示。分析图5~图7可知:当小球从右向左移动时,前侧不断靠近低压区,当小球最高点到达油道端面(设为P0)的左侧时,后侧静压力迅速升高,此时小球加速度大幅增加,迅速移动到喉口位置,完成球阀关闭。
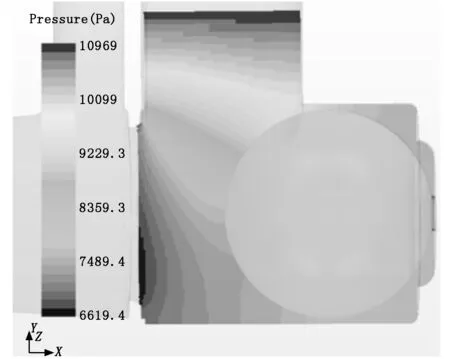
图5 X=0 mm,Fpx=-9.1×10-2 N时的压力云图

图6 X=-2 mm,Fpx=-9.9×10-2 N时的压力云图
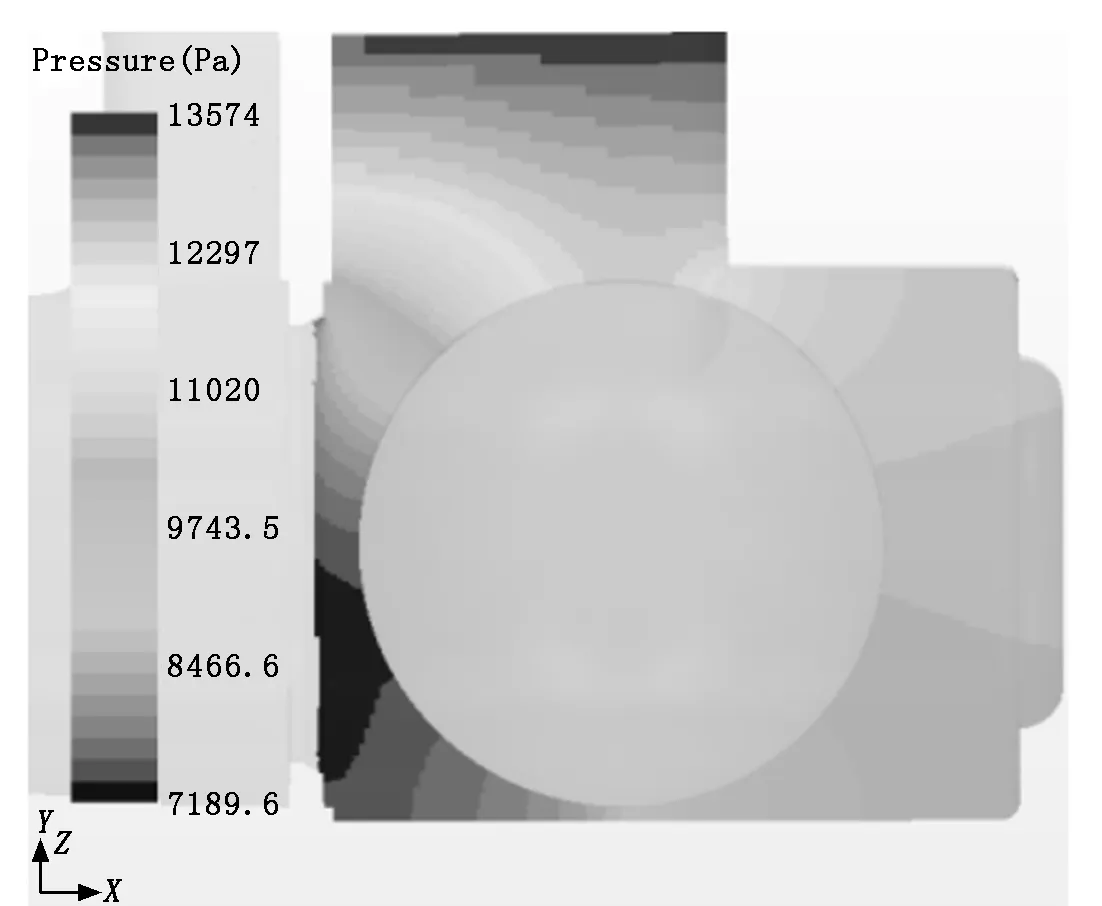
图7 X=-4 mm,Fpx=-2.2×10-1 N时的压力云图

表2 仿真计算结果
2.2 流量对球阀的影响
方案1、2、3、4计算了不同进口流量作用下球阀特性,计算结果如图8、图9所示。 结果显示小球运动过程可以大致分为两个阶段:第一阶段小球在喉口侧低压的“吸附”作用下,以一个较低的速度v1近似匀速运动(后侧静压基本不变),随着流量增大,喉口的压降越高,同时在流体冲刷下小球旋转越快,最终导致运动速度v1越大,该阶段大约占球阀关闭总时间的一半;当小球缓慢移动到油道端面(P0)开始进入第二个阶段,小球右侧静压力开始增加,小球所受的“吸力”和“推力”同时增加,导致运动速度和加速度迅速增加,直到小球移动到末端,球阀完全闭合。从图8、图9可以看出:流量越大,球阀关闭用时越短,但是小球落座速度越大。虽然单向阀响应特性更加优越,但是小球落座速度变大可能会加剧小球回弹和碰撞现象,引起系统压力波动和阀体磨损。
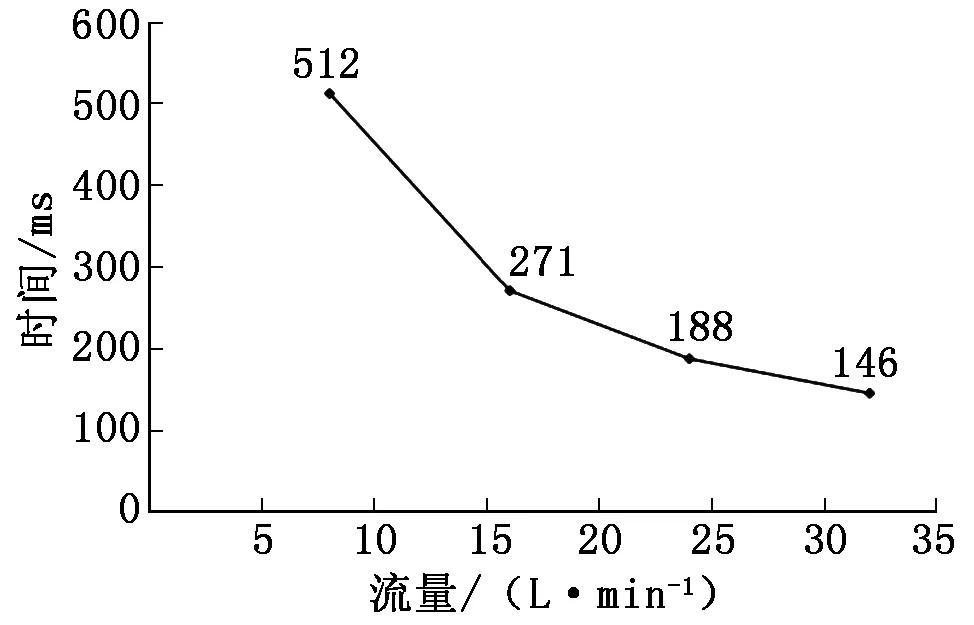
图8 不同流量下球阀关闭时间
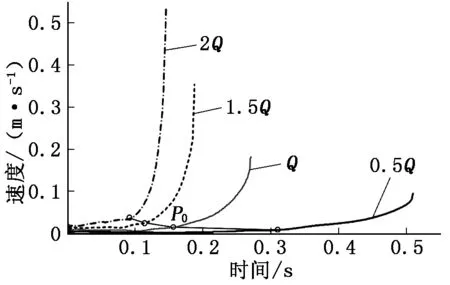
图9 不同流量下小球运动速度
分析认为P0位置和流量直接影响球阀性能。当球阀流量较小,同时球阀需要达到较高的响应特性时,工程师可以调整小球和P0的距离,以缩短或者除去第一阶段的缓慢运动,直接使小球加速关闭。当球阀流量较大,同时球阀没有太高响应要求时,可以将小球置于P0之后,既可以增大通态时球阀的流量系数、降低球阀压降,又可以使小球在闭合的第一阶段获得较大的运动速度v1,使小球关闭时间不会太长。因此工程应用中需要根据球阀使用的流量范围,选择最优起始点P0。
2.3 小球质量对球阀的影响
方案2、5、6、7研究了不同小球质量对球阀特性的影响,小球运动过程如图10所示。由图10可以看出:小球质量减小可以缩短球阀关闭时间。由于小球质量减小,小球缓慢移动到P0左侧后,开始加速运动,越小的质量获得的加速度越大,小球也将最快到达喉口,完成球阀闭合;同时还发现4种情况下小球在第一阶段运动速度较为相似,这也再次说明该阶段小球基本上处于匀速运动状态,因此单向阀小球在第一阶段速度v1将会是一个非常重要的参数。考虑本文计算初始时刻边界条件会对该速度产生较大影响,此处未能得出该速度的产生机理和影响因素。
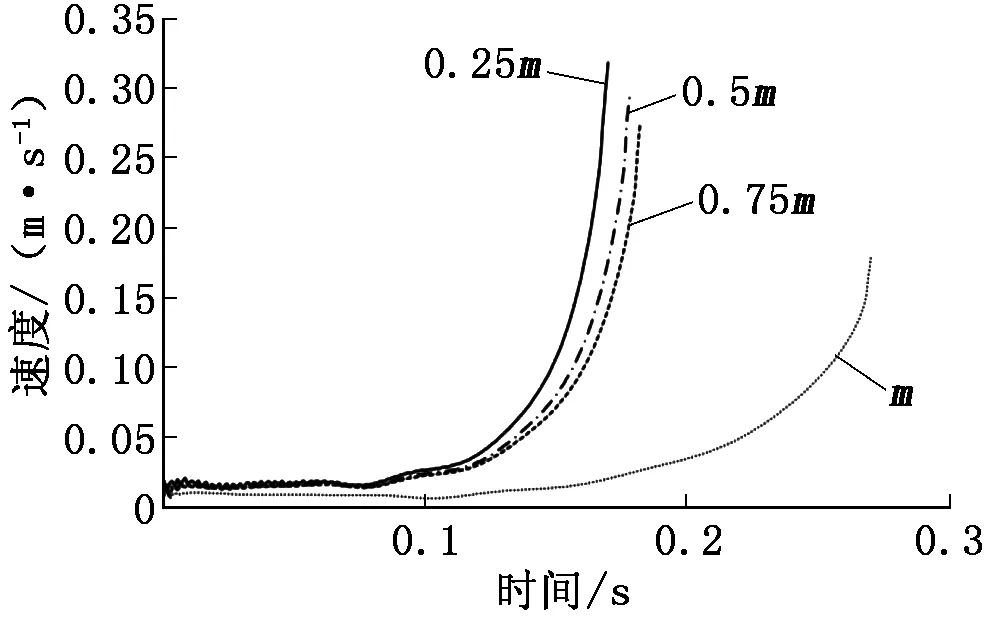
图10 不同质量下小球的运动速度
3 结论
本文采用嵌套动网格方法研究了单向球阀自由关闭时的运动特性,比较了单向阀流量和小球质量对小球运动的影响,得出以下结论:①单向阀关闭时,小球主要受到静压力的作用,当小球移动到P0点左侧后,静压力迅速增加,使小球加速运动完成单向阀关闭;②小球整个运动过程分为第一阶段近似匀速运动和第二阶段加速运动,以P0点位置作为分界点;③流量越大小球获得越大的第一阶段速度v1,质量越小,获得越大的第二阶段加速度。同时,小球第一阶段速度v1的形成机理还未解释清楚,作者后续将重点研究单向阀闭合前状态和闭合条件对第一阶段速度v1形成的影响。

