基于改进Dijkstra算法的AGV路径规划研究*

李全勇，李 波，张 瑞，姜 涛

(1.内蒙古一机集团力克橡塑制品有限公司 技术中心，内蒙古 包头 014000；2.湖北文理学院 机械工程学院，湖北 襄阳 441053；3.武汉科技大学 机械自动化学院，湖北 武汉 430081；4.北京星航机电装备有限公司 技术中心，北京 100071)

0 引言

自动导航运输车(AGV)作为智能物流的核心设备，广泛应用于汽车、食品、烟草、医疗、服装等行业。路径规划是AGV应用的核心技术之一，对其进行研究具有极高的工程价值。文献[1]提出了一种基于时间最短的无碰撞路径算法；文献[2]在AGV调度算法中计入空闲时间，基于遗传算法进行调度规划；文献[3]将改进遗传算法应用于AGV避障路径规划；文献[4]研究了细菌势场算法，求解移动机器人静态和动态路径规划；文献[5]在车间调度中引入了灰狼优化算法，预测工件到达时间；文献[6]提出了改进重力搜索算法，仿真实现了在静态障碍物下的路径规划；文献[7]采用Dijkstra算法求解单台AGV最短路径，实现AGV的智能无线控制；文献[8]提出一种改进型蚁群路径规划算法，加入全局信息素更新机制,提高了算法的搜索效率；文献[9]以最小化最大搬运完成时间为目标，研究了一种生成无路径冲突的路径规划算法；文献[10]采用遗传算法对改进蚁群算法进行参数优化，以提高收敛速度，避免局部最优。

针对磁导AGV运行特点，本文进行了基于栅格法的拓扑地图建模，分析了A*、蚁群、遗传、Dijkstra算法的AGV路径规划问题，引入路径平滑度，并以时间权重为优化目标求解最优路径，提出了改进Dijkstra算法，开发了路径规划仿真系统，进行了多种算法AGV路径规划对比分析。

1 AGV地图模型构建

地图模型构建是AGV路径规划的基础，直接影响路径规划算法的设计。本文基于栅格法的无向有权拓扑地图方法，开展AGV运行环境的建模，如图1所示。

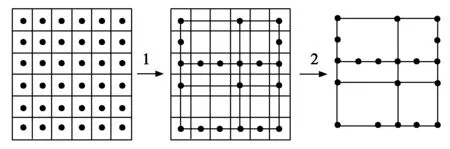
图1 地图建模

以栅格图为基础，每个网格中心为节点，连接相关节点作为边，其代表路径规划中的磁导线。保留图中节点和边，去除网格，剩下部分为拓扑地图的地图模型。

2 基于改进Dijkstra算法的AGV路径规划

针对拓扑图下的AGV路径规划问题，A*算法求解最短路径，但由于受到估计代价值的影响，算法出现局部最优，稳定性不佳；蚁群算法虽能得到强鲁棒性的优化路径，但对全局搜索能力较低，收敛速度较慢，容易在搜索过程中陷入局部最优；遗传算法具有良好的搜索能力，不易陷入局部最优，但局部搜索能力较差，进化后期搜索效率较低，需对算法本身参数进行优化，避免过早收敛。

Dijkstra算法[11]作为一种贪心算法，以起始点为中心源点层层向外扩散直至搜索到所有节点的最短路径。其根据路径总权重来获得最短路径，两节点之间权重使用一般直线距离公式求解：

(1)

传统Dijkstra算法作为典型的最短路径算法，可准确获取全局最优路径，通常将路径长度作为权重因子搜索最短路径，但无法考虑到路径平滑度对AGV实际运行中的影响。

本文提出以时间权重作为最优路径的考虑因素，通过模拟AGV从起点至终点运行花费的总时长，对比AGV在各个可行路径中的运行最短时长，筛选出最优路径。时间权重T函数表达式为：

(2)

其中：Dij为节点i、j之间的距离；U为AGV在路径直线部分的平均速度；TΦ为弯道总权重，表示AGV经过所有弯道时间权重；Tij为时间总权重，表示AGV从节点i到节点j总权重。弯道总权重函数表达式为：

(3)

其中：S(i,i+1)为首尾分别为节点i与节点i+1的边；tΦ为两条相邻边夹角的权重。

AGV在巡线过程中面对不同角度弯道做出不同动作，其中夹角权重如式(4)所示：

(4)

其中：R为拐弯类型标识符，R=0表示角度弯，R=1表示为弧度弯；r为拐弯半径；c为转弯因子，根据不同AGV拐弯机制设定，值为常量，用U·c表示AGV拐弯角速度；wβ为减速因子，用于弧度弯道中，表示AGV过弯时减速程度；W为旋转精度惩罚因子；Φ为转角角度；tw为减速损耗权重，用于表示减速带来的时间损耗，表达函数为：

(5)

其中：dw为减速缓冲距离(减速节点与转弯节点的距离)；wα为减速因子，表示AGV进入弯道前的减速程度，wα≤1。

AGV经过不同角度弯道时会产生不同层次时间损耗，根据这一特性，依据角度Φ的不同，将夹角权重tΦ分为三个阶段分析求解：

第一阶段(0≤Φ≤Φ1)：转弯夹角很小，此类弯道所产生时间损耗为0。

第二阶段(Φ1<Φ≤Φ2)：弯道夹角适中，AGV无法通过自动巡线功能通过此类弯道，可在弯道夹角放置拐角节点，根据信号依次完成急停、准确地旋转相应角度、恢复巡线速度等动作。

第三阶段(Φ2<Φ≤Φ3)：当弯道夹角过大，AGV无法旋转至相应角度，会产生或多或少的旋转角度误差。此时，AGV会通过自身巡线功能，以拐角节点为中心左右旋转寻找磁导线。随着拐弯夹角的增大，产生的误差角度也会增大，随之带来的巡线损耗时间也会增加。为此提出W旋转精度惩罚因子，可根据不同AGV自身的性能设值。

通过对两夹角的权重分析，最优路径权重可由式(6)表示：

(6)

3 仿真验证

采用C#语言开发了Winform应用程序，进行了多算法仿真实验。图2为AGV仿真平台界面截图，采用栅格法拓扑图进行车间地图布局。

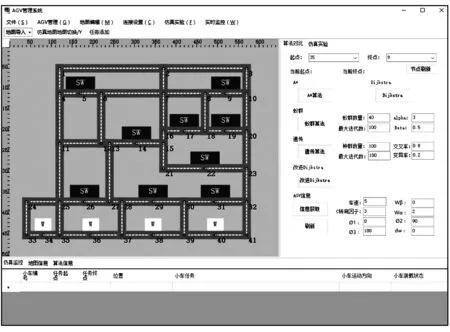
图2 仿真界面

根据图1地图模型，将41个节点与53条边信息录入系统，完成实验数据初始化。地图拐角信息主要采用角度弯道，U=5(以模型比例设置)，wα=2，wβ=0，Φ1=0°，Φ2=90°，Φ3=180°，c=3°，dw=10，W=0。通过选择不同任务起点与终点进行实验，结果如表1所示。

表1 实验数据表

通过多次实验，选择三组特征值最明显的数组进行对比，主要结论如下：

(1) 蚁群算法与遗传算法在求取最优路径时具有不稳定性，在多次求解过程中会出现多个长度相同、但是拐弯次数不同的路径，在迭代次数不足的情况下，蚁群算法更是无法获取路径长度最短的解。

(2) A*算法、遗传算法、改进Dijkstra算法的稳定性更好。

(3) 改进Dijkstra算法每次获取路径都为最优解(理论用时最短)，求得路径长度虽大于其他路径算法，但理论用时依然是最少。

为进一步验证算法的可靠度，开展了120个节点车间环境的仿真实验，布局如图3所示。

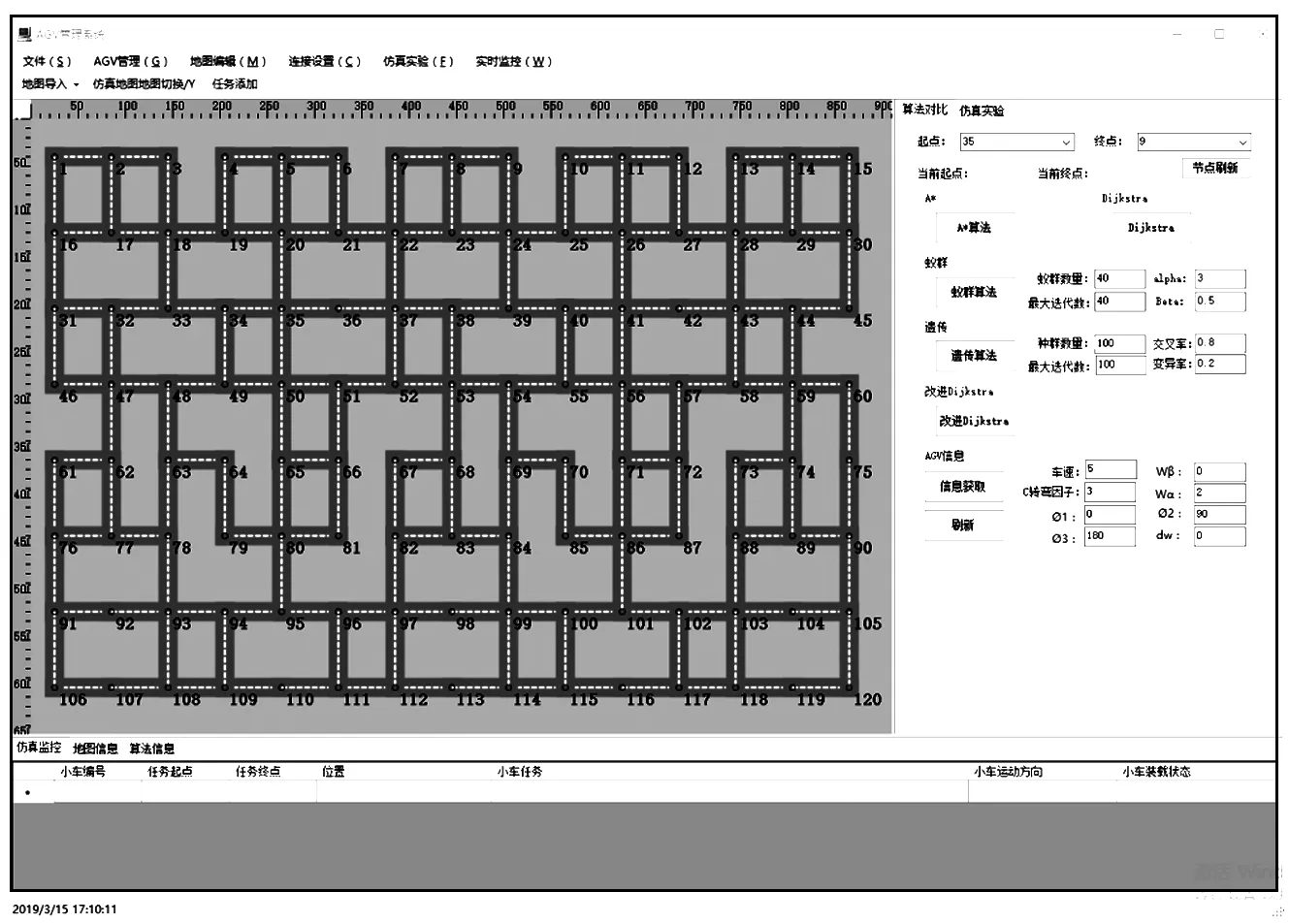
图3 地图模型

120个节点使用了无规律的连接来降低实验环境的平滑度，总共有173条连接线。仿真实验以1号节点为起点，选择图中一系列坐标点作为实验终点进行多次验证。

采用蚁群算法与遗传算法分别对每组数据进行100次实验并提取平均值，进行实验数据对比。其中蚁群算法参数设置为：蚁群数量40，最大迭代次数40,alpha=3，beta=0.5；遗传算法参数为：染色体数量50，最大迭代次数20，最大变异次数20，交叉率0.8，变异率0.2。实验数据对比如图4所示。

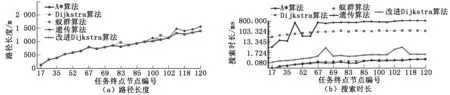
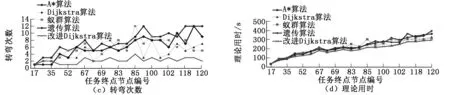
图4 仿真数据对比

4 结语

本文基于栅格的无向有权拓扑方法，建立了AGV系统仿真地图模型；分析了A*、蚁群、遗传和Dijkstra算法，针对上述算法在拓扑图中的适用性问题，提出了改进的Dijkstra算法，引入路径平滑度，以时间权重为优化目标求解最优路径；基于仿真平台，开展了上述算法在拓扑地图模型的实验对比，测试结果表明：改进Dijkstra算法在路径拐弯次数、模拟运行时间等方面具有良好表现。