基于SVR误差补偿技术的神经网络城市污水厂水质预测
冯 骁,夏文泽,王 喆,*,钱志明,刘 杰,许雪乔
(1.北京华展汇元信息技术有限公司,北京 100044;2.北京首创股份有限公司技术中心,北京 100044)
作为一个水资源极度紧缺的国家,我国的水环境现状不容乐观,为了维护人们的正常生活,与用水相关的污水处理越发被重视。其中水质预测对于污水处理的优化调度与精准控制起到了极大的作用,比如对出水总氮,浓度预测就是评价水处理效果及程度的关键指标之一[1]。但是从预测控制系统的设计角度看,城市污水处理系统由于污染物质的多样性、繁杂性和变化性,该系统变为难以预测控制的复杂流程。这些复杂特征主要体现在以下几个方面:研究对象的复杂性、研究环境的复杂性、工艺任务的复杂性以及处理过程中包含多目标融合的复杂性,均使城市污水处理过程难以被很好解析及映射[2]。
基于上述原因,根据传统工艺控制理论的城市污水处理过程控制系统难以取得满意的预测及控制效果。而近年来在国内外,控制领域神经网络预测控制系统已被广泛应用[3]。该类系统自身具有自学习、自适应和自组织功能,特别是在模型搭建之初,无需建立数据对象精确机理关系的特点[4],可相对有效地用于复杂城市污水处理过程的映射工作,但并不是所有映射结果都十分准确。由于神经网络模型的自身特点,它映射城市污水处理过程中必定处于模拟黑盒状态,无法很好地诠释控制系统的机理,使模型在模拟过程中会出现随机误差现象,致使控制系统无法做到准确映射污水处理过程并加以控制[5]。不仅如此,国外学者研究表明,由于误差噪声的引入,神经网络会更突显其自适应特征的属性,使模型输出结果更具模糊效果[6]。这类性质在某些领域具有优势,但在精准工控领域存在致命问题,这也是本文在研究中想要避免的方向。
对此,本文研究一种基于SVR误差补偿技术的神经网络城市污水厂水质预测模型。该模型使用BP神经网络预测出水总氮水质,并利用预测误差搭建补偿模型,对预测结果出现的随机误差进行校正,起到提升水质预测精准度的作用,并最终达到准确调度城市污水厂污水处理系统的目的。同时,本文还尝试利用马尔科夫概率补偿的方式进行随机误差的校正,但精度提升效果不如SVR补偿模型,这也说明SVR模型在误差补偿方面体现的强大性能。
1 理论
1.1 模型架构
本文根据研究内容制定了模型架构,如图1所示。该模型分为两个模块,其中一个为训练模块,另一个为水质预测模块。在训练模块中,先将历史模型分为两份:利用第一份历史数据搭建历史清洗模型,并对已有数据进行清洗,再将清洗结果训练BP神经网络;利用另一份历史数据通过数据清洗与训练好的BP神经网络预测,得到预测误差,利用此误差搭建SVR补偿模型或马尔科夫补偿模型。在预测模块中,利用当前实际数据进行数据清洗与BP神经网络预测,并用前一时刻的预测误差进行补偿模型的换算对预测结果进行补偿,最终得到校正后的预测结果。

图1 模型架构图Fig.1 Model Architecture
1.2 数据清洗
数据清洗是水质预测的必要步骤,可有效提高水质预测的准确度。一般情况下,对于稳定运行的大型城市污水处理厂,其历史输入水质数据都有一定的关联性。根据这一性质,本文提出了一种历史模型数据清洗算法,其主旨思想是利用已稳定运行的城市污水厂的历史数据构建清洗算法模型,然后通过模型对新输入的水质数据进行跳变值清洗。本文从两个维度对输入水质数据进行数据清洗,分别为单变量自我纵向清洗和多变量综合横向清洗。
1.2.1 纵向清洗方法
纵向清洗是指利用单一指标本身数值出现的频率构建统计模型,对大概率(95%以内概率)数值出现范围进行标定,并用此标定范围对新数据源进行清洗。具体步骤如下。首先,将某一指标的值域通过kmeans聚类算法分为50份[7],值域分配如式(1),数据集质心更新如式(2);然后,再对所有已分类的数据集合中的点数进行统计,最后求出大概率值域。
(1)
其中:dist()——标准L2欧式距离;
C——所有已分类的数据集合的质心集合;
ci——第i个数据集合的质心;
xj——待分类的数据点。
(2)
其中:Si——已分配的第i个数据集合;
Ni——已分配的第i个数据集合的点数;
ci——第i个数据集合的质心;
xj——待分类的数据点。
1.2.2 横向清洗方法
横向清洗是指利用各个指标之间的关系建立关系向量,例如考察入水总氮指标时,需要联系入水水量、入水COD、入水氨氮和入水温度等指标综合分析。首先,根据指标间的关系建立关系向量,再计算新旧向量间的余弦角度与马氏距离;然后,加权处理后清洗掉小概率5%占比的奇异点数值,余弦角度如式(3),马氏距离如式(4);最后,需对两种横向计算结果进行加权综合,再对横纵两部分所得清洗结果进行并集处理,并最终得到清洗结果。
(3)
其中:Ai、Bi——新旧关系向量;
n——向量包含个数。
(4)
其中:xi、xj——新旧两个关系向量的数值;
S——协方差矩阵。
1.3 基于马尔科夫链补偿的神经网络预测误差模型
马尔科夫链是指数学中具有马尔科夫性质的离散事件随机过程。在其事态发生过程中,系统根据概率分布可以从一个状态变到另一个状态,也可以保持当前状态。其实质是系统针对事态当前状态对于即将发生的情况进行概率预测,即根据目前状况来预测其将来时刻变动状况[8]。应用到水质预测领域,就是根据BP神经网络的上一时刻输出误差,预测这一时刻各种误差情况的概率,具体操作如下。
在事态发展变化过程中,先设所得数据过程为符合马尔科夫性质的随机过程,它的序列状态可表示为...,Xt-2,Xt-1,Xt,Xt+1,...,而在时刻Xt+1状态的条件概率仅仅依赖于时刻Xt,如式(5)。
P(Xt-1|...Xt-2,Xt-1,Xt)=P(Xt+1|Xt)
(5)
此时可以根据序列性质设定其包含m个可能状态,如式(6)~式(8)。
(6)
(7)
(8)
其中:m——利用误差均值与标准差分级方法划分为几级;
fij——序列状态从i经过一步转移到状态j的频数;
Pij——转移概率;
P*j——相应的边际概率;
χ2——马氏统计量[8]。
利用卡方检验验证所得马氏统计量是否大于卡方边界值,大于则满足马氏性,小于则不满足马氏性[8]。经验证,以预测误差所得结果划分的误差区间矩阵满足马氏性,即可以利用转移概率组成的转移概率矩阵表达下一步水质预测误差状态,其中转移矩阵效果如式(9)。
(9)
综上所述,依据概率矩阵得到补偿误差向量,并根据补偿误差向量输出预测结果。
1.4 基于SVR误差补偿技术的神经网络水质预测模型
SVR(support vector regression)全称是支持向量回归机,它是SVM(support vector machine)支持向量机对回归问题的一种升级运用。SVM与逻辑分类器类似,是一种二分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略是间隔最大化,SVM问题最终可以转化为一个凸二次规划问题的求解模型。如图2所示,SVR回归与SVM分类的区别在于,SVR的样本点最终只有一类,它所寻求的最优超平面不是像SVM那样使两类或多类样本点分的“最开”,而是使所有的样本点离着超平面的总偏差最小[9]。这些属性的直白理解为SVM是要使超平面与各个最近样本点集合的“距离”最大化;而SVR则是要使超平面距最远样本集合点的“距离”最小化。因此,利用SVR的特点属性求最优解的过程就是将已有的预测模型误差集合通过超平面技术求得最佳描述的过程[10]。此外在国外学者研究过程中,已将它与神经网络模型相结合,并应用于工控领域,且取得了良好的效果,如在数控机床热误差检测、大气污染物浓度预测以及污水处理厂水质预测等方面均得到广泛的应用。而引发此现象的原因是SVR本身所具有的严格数学理论特性、直观的几何解释和良好的泛化能力, 可以以任意精度逼近任意函数, 并能有效避免神经网络因欠学习和过学习所引发的梯度爆炸现象[11],尤其在处理小样本训练学习问题上具有独到的优越性[12]。

图2 SVM与SVR的对比图Fig.2 Comparison between SVM and SVR
SVR本质是通过一个非线性映射将不能线性回归的样本数据映射到高维进行线性回归[13],该回归的函数表达如式(10)。
f(x)=wTφ(x)+b
(10)
如前所述,SVR满足两个性质,第一个性质要求所有的样本点离着超平面的总偏差最小,第二个要求回归值与真实值偏离程度不太大,即无需计算损失,因此,SVR的目标函数表达如式(11)。
(11)

(12)
s.t.
(13)
通过拉格朗日方法求解式(12)~式(13)[14],并根据对偶原理进行对偶转化得到式(14)~式(15)。
(14)
s.t.
(15)

K(xi,xj)——核函数;
c——惩罚因子。
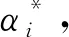
(16)
2 试验
2.1 数据选取与准备
本试验数据是南京市某城市污水处理厂的真实数据,该厂工艺为AAO工艺。该污水处理厂内可得的指标主要为进水水质参数、过程量参数及操作参数,这些参数分别为进出水处在线仪表所获参数、厂内重要水处理构筑物内在线仪表所获参数,以及厂内涉及运营策略的设备运行参数。为保证预测质量,本研究的输入值需覆盖三类指标,以保证输入参量的全面性[15]。由于厂内可获得参数的限制,刨除输出参量外,所测指标仅为13种模拟参量,其中属于操作参数的指标有二沉池回流量。(1)选取二沉池回流量作为操作参数。(2)属于过程量参数的指标有厌氧池ORP、厌氧池电导率、混合池溶解氧、好氧池氨氮、好氧池溶解氧,这些指标均直接参与,甚至直接指示水处理过程氨氮的代谢行为,因此全部选取。(3)属于进水水质的指标包括进水COD、氨氮、总氮、总磷、水量、温度及pH,但由于所选择的时间段仅为1月内的数据,温度和pH无明显变化,二者只作为指示参数进行常规记录相当于常量,温度和pH不纳入模型输入变量。此外方差过小的数据对BP神经网络的训练会产生影响,因此,本文选取除温度和pH以外的指标作为进水水质参数[16]。最终选取的模型输入值与模型预测值如表1所示。
所有试验数据包含连续8 d共1 152组数据,每个数据时间间隔10 min。将这些数据按照数据清洗规则进行清洗筛选,其中横纵数据清洗权重为1∶1,清洗效果如图3所示。由图3可知,数据集中异常数值被删除,清洗数据占比为总数据集的11.02%,最后剩余数据1 025组,这些数据中有820组数据设定为训练集,剩下205组数据为测试集[17]。

表1 模型输入参量与预测参量Tab.1 Model Input and Output Parameters
2.2 BP神经网络训练
本次试验 BP 神经网络结构设计为 4 层网络,一层输入网络,两层隐藏层网络,节点分别为15和3,最后一层为输出网络[18]。模型优化器选择为Adam[19],学习率初始为0.01,每隔100个epoch学习率减小为原来的1/10,计算损失值以均方误差结算(MSE)作为模型精度的评价指标。MSE的表示如式(17)[20]。

图3 数据清洗效果Fig.3 Result of Data Cleaning
(17)
其中:n——数据集大小;
G——网络模型,根据样本x输出预测向量G(x)。
模型训练完成后,损失函数降低效果如图4所示,可知损失函数数值已从8控制到0.005以下[21],说明模型已学到输入参数与输出参数之间的映射关系。

图4 损失函数训练效果Fig.4 Training Effect of Loss Function
2.3 SVR补偿模型试验
搭建SVR计算模型需在SVM模型基础上进行,即在SVM的分类基础上引入不敏感损失函数,从而得到回归型支持向量机SVR数学模型[22]。其中具体模型参数及步骤如下:
(1)利用BP神经网络进行水质预测,并输出误差数据集;
(2)将误差数据集分为训练集和测试集(8∶2分布),且需要说明的是SVR输入为误差数据,输出为误差补偿值;
(3)对所有数据进行归一化处理;
(4)寻找SVR模型的最佳c参数(惩罚因子,误差宽容度,范围是-10~10,步进0.5)以及g参数(RBF函数的gamma,决定数据映射到新特征空间后的分布,范围是-10~10,步进0.5)[23];
(5)创建训练SVR模型,设置epsilon-SVR为损失函数,且epsilon设为0.1,径向基函数选为:exp(-gamma*|u-v|2)[24];
(6)利用数据集对SVR模型进行仿真。
2.4 马尔科夫对比试验
利用马尔科夫链组成概率补偿模型进行误差补偿的对比试验[25]。先建立分级区间,利用训练数据集的误差矩阵均值μ与方差σ搭建6级分级区域,一般可将数据矩阵分级为:(xi>μ+σ),(μ+0.5σ 本次试验验证数据是依据上述南京市某污水处理厂的测试集数据整理得来,总共205组试验数据,结果如图5所示。 图5 预测结果Fig.5 Forecast Results 图5是BP神经网络、SVR模型与马尔科夫模型的预测结果图,图中纵坐标是总氮输出值,横坐标是样本数(样本顺序按照时间排列),曲线为各模型预测数值的结果曲线。试验结果如表2所示,SVR补偿模型预测的测试集数据波形与测试集真实值数据波形相关度为0.93,高于其他两种预测方式,该结果说明其曲线外形最为相似;且SVR补偿模型预测值与真实值结果的欧氏距离为3种预测差值的最小值,达到0.256,说明SVR补偿数值最接近真实值。通过以上结果可以表明,SVR补偿模型预测数据最为准确[26]。 表2 预测对比结果Tab.2 Results of Forecast Comparison 图6 误差结果Fig.6 Error Results 图6是真实值与预测模型结果之间的误差结果图,曲线越接近0说明预测值与真实值越接近。图中纵坐标为总氮的预测误差,横坐标为样本数(样本顺序按照时间排列),曲线为各模型预测误差数值。其中,纵坐标的0值虚线表示0误差,即无误差结果。利用平均绝对误差(AAE)、均方误差(RMSE)以及广义终值误差(GFVE)指标分析SVR、马尔科夫的补偿结果[27]。由表3可知,SVR补偿结果的各项误差值均比马尔科夫补偿误差以及无补偿误差小,说明SVR补偿具有更小的稳态误差,且其结果波动小,准确性更高。 表3 误差对比结果Tab.3 Error Comparison Results 通过试验,可以看到SVR的预测数据精度优于BP神经网络单独预测的精度,且其预测结果也优于马尔科夫链误差补偿的预测结果。 针对城市污水厂污水处理反应过程复杂性及模糊性的特点,本文先以历史模型对数据进行清洗,有效提高了数据输入质量,之后再以BP神经网络为基础设计开发了SVR误差补偿模型,弥补了普通神经网络对黑盒模型随机误差、机理误差反应不足的现象,有效提高了预测水质结果的准确性。具体预测过程为:首先,通过城市污水厂传感器收集到某一时刻的输入数据;然后,通过数据清洗算法对输入数据进行清洗;接着,将清洗过后的数据送入在训练数据中训练好的BP神经网络,得到此时刻的预测输出;再将前一个时刻BP网络预测值与真实输出值的误差值送入早已训练好的SVR模型,得到此时刻的补偿值;最后,将BP网络输出的预测值与SVR输出的补偿值求和得到此时刻最终的预测输出值。 此外,本文方法还存在一定的提升空间。第一是神经网络预测模型的改进,通过研究可知污水处理是一个具有时序性质的过程,但简单的BP神经网络无法做到对时序性的描述,而以RNN、LSTM为首的循环神经网络就可以做到,因此,之后的神经网络改进工作可以参考这个方向进行[28]。第二是对上报数据的清洗,本文清洗的重点是围绕数据层面,着重以数学逻辑进行清洗;但在工艺层面涉及不多,因此,之后数据清洗工作可以多从工艺逻辑方面着手研究。2.5 试验结果

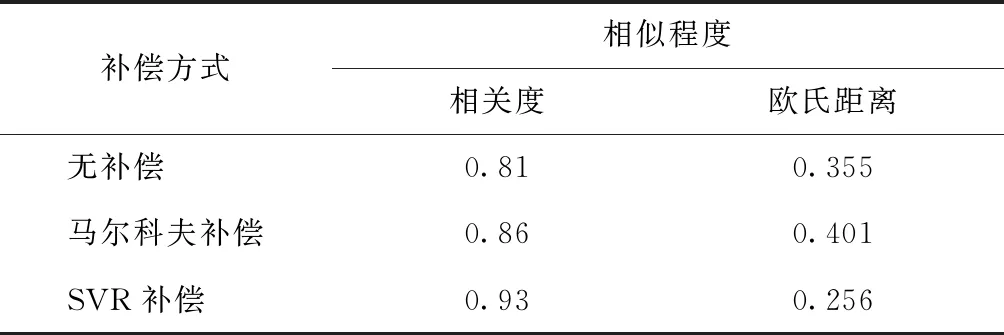


3 结论与展望

