一类延迟型禽流感模型的稳定性分析

戴晓娟

(宁夏师范学院 数学与计算机科学学院,宁夏 固原 756000)

1 模型的建立

H7N9亚型禽流感病毒是甲型流感中的一种,它对全球经济和人类健康造成了严重影响.为了防止H7N9禽流感从家禽向人传播,卫生部门采取了一系列措施,例如关闭活家禽市场,屠宰和隔离流感禽等[1].但是,尚未完全了解H7N9禽流感的传播动态.因此，本文借助禽流感数学模型,通过开发、比较、实施,评估等措施对H7N9禽流感进行检测和控制.

本文将提出一种新型的禽流感模型,并讨论时间延迟对疾病传播的影响.首先,分别模拟了禽类和人类种群的动力学系统,建立了适合两种种群系统的禽流感模型[2-5],其次,要求被感染的禽类持续处于疾病状态,不能康复.而被感染的人可以康复,并且康复的人要获得永久的免疫力.

故假设禽类种群和人类种群分别为Na(t),Nh(t),其中禽类种群的总变量取决于疾病状态的易感和感染群Sa(t )和Ia(t),人类种群取决于疾病状态的易感人群,感染人群和恢复人群,即Sh(t)和Ih(t),Rh(t).同时假设所有的禽类和人类都易感.

故延迟型的非线性禽流感模型如下

(1)

模型(1)中的所有参数均非负,描述如下:Λa代表禽类的自然增长和新生数量，βa代表禽类从感染到易感染性的传播率，μa和δa分别代表禽类种群的自然死亡率和与疾病相关的死亡率,δ1和δ2分别代表禽类易感染种群和感染种群的屠宰率，Λh代表人的新增数量和新生儿数量，βh是感染禽类向可感染人类的传播率,μh是人类的自然死亡率,δh是感染人群得病的概率,γ是感染人群的恢复率.

在时间t-τ1处感染的禽(或在时间t-τ2处感染的人类)从时间t开始具有传染性,可以用βae-μaτ1S(t)I(t-τ1)(或βhe-μhτ2S(t)I(t-τ2))表示t时刻被感染的禽(或人类)种群的传染性,其中e-μaτ1(或e-μaτ2)是被感染的禽类(或人类)存活到t时刻的概率,以此表示时间延迟.用-δ1Sa(t)和-δ2Ia(t)表示易感和传染禽类的屠宰率,因为禽屠宰作为一种人工造成的死亡,在一段时间内可以显著提高禽畜的死亡率.

备注1实际上,当禽类被屠宰时,往往无法区分易感禽类种群和感染禽类种群.所以δ1和δ2的值可以相等,这是模型(1)的一个特例.又因为恢复的种群对Sh,Ih的动力学没有影响,因此本文未考虑恢复的相关情况.

所以系统(1)可以变为下列系统

(2)

该系统的初始条件为

(3)

其中τ=max{τ1,τ2},R+={x∈R:x≥0}.

系统平衡点的稳定性通常由称为基本再生数R0的阈值控制,它是处于感染期的感染个体在完全易感人群中产生的继发感染数.对于模型(2),基本再现数可以计算为[6-7]

系统(2)有两个平衡点

定理1系统(2)在初始条件(3)下的解为正且有界的,即存在一个正不变集[8].

证明由系统(2),有

(4)

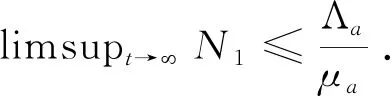
备注2定理1证明了系统(2)的解是非负的,即现实世界中,禽类和人类的数量是非负的.

2 平衡点的稳定性分析

下面讨论无病平衡点和地方病平衡点的稳定性[9-10].

定理2如果R0<1时,系统(2)的无病平衡点E0是局部渐近稳定的;如果R0>1,则是不稳定的.

证明系统(2)的特征方程如下

(5)

由(5)得出,前三个特征值是

λ1=-(μa+δ1),λ2=-μh,λ3=-(μh+δh+γ),

都是负的.考虑方程(5)的其余特征值,即下面方程的根

(6)

如果τ1=0，R0<1,则λ4=(μa+δa+δ2)(R0-1)<0,而当R0>1时，λ4>0.因此,当τ1=0，R0<1,无病平衡点E0是局部渐近稳定的.

令λ=iv,v>0是一个实数且i2=-1,代入(6)式,将实部和虚部分开,得到

(7)

将(7)式两边平方并相加,得

(8)

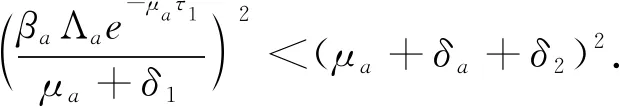
在定理2中,当R0>1时无病平衡点E0不稳定,下面讨论R0<1情况下无病平衡点E0的全局渐近稳定性.

定理3当R0<1时,系统(2)的无病平衡点E0是全局渐近稳定.

证明仅考虑系统(2)的前两个方程,即以下仅禽类的子系统

(9)

(10)

则

(11)

(12)

对于上述系统,定义一个Lyapunov函数为

(13)

因此,

(14)

定理4如果存在R0>1,则系统(2)的地方病平衡点E*是局部渐近稳定的.

证明平衡点E*处的雅可比矩阵

相应的特征方程为

(15)

相当于

[λ+(μa+δ1)R0](μa+δa+δ2+λ)=(λ+μa+δ1)(μa+δa+δ2)e-λτ.

(16)

当R0>1时,(16)解的实部是非负的,则得到

|λ+(μa+δ1)R0|>|λ+μa+δ1|,|μa+δa+δ2+λ|>|μa+δa+δ2|,|e-λτ|≤1.

(17)

因此,在(16)中,左侧的模大于右侧的模,这导致了矛盾.因此,(15)的所有根都应具有负实部.所以,地方病平衡点E*是局部渐近稳定的.

下面,研究E*的全局稳定性.通过以下定理将证明R0是模型(2)的阈值.

定理5当R0>1时,系统(2)的地方病平衡点E*是全局渐近稳定.

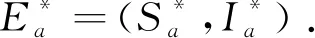
(18)

其中,

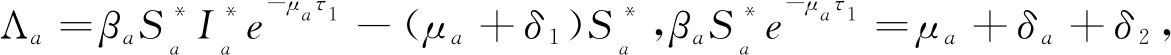
因此,有

(19)

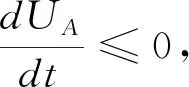
(20)

定义一个Lyapunov函数:

UB=U4+U5，

(21)

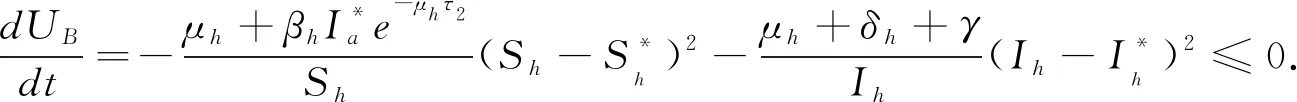
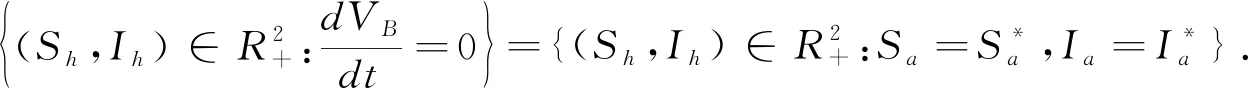
备注3定理3和定理5表明,如果R0<1，禽流感将消亡;而如果R0>1，禽流感将流行.由此说明R0是模型(2)的阈值.

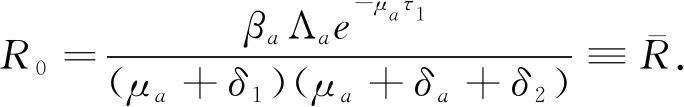
3 结论

本文研究了一类带有禽屠宰的延迟型禽流感模型,利用稳定性理论对模型进行了分析,证明了该模型唯一的全局正解,并通过构造适当的Lyapunov函数,利用LaSalle的不变性原理,建立了模型无病平衡点和地方病平衡点的全局稳定性,即当R0<1，禽流感将消亡;当R0>1，禽流感将流行.此结论说明时间延迟可以抑制禽流感的爆发,帮助公共卫生机构控制流行病的传播.