基于有向无环图的倒排链等字长划分压缩算法

（1.西安理工大学计算机科学与工程学院，西安 710048；2.陕西省网络计算与安全技术重点实验室（西安理工大学），西安 710048；3.中国人民解放军63785部队，西安 710043）

0 引言

不断增长的互联网网页规模给搜索引擎系统的倒排索引存储带来了持续的挑战和研究需求［1-2］。近年来，大量互联网应用的蓬勃发展更使搜索引擎系统待索引的数据规模进一步增加［3］。一般来说，倒排索引包括倒排文件和词典文件，倒排文件包含着一串被压缩的倒排项信息：文档号（docid）和词频（freq），其中文档号可以转换为更小的d-gap 整数序列。倒排索引压缩的目的就是采用尽可能接近最优位（bits）数的码字存储原来以一个机器字长表示的倒排信息整数，同时保证对码字解压的无歧义和高效性。倒排索引压缩技术的优势在于可以降低压缩数据的存储开销和传输开销，从而实现对海量压缩倒排索引数据的快速内存查询访问［4-5］。因此，倒排索引压缩技术一直以来都是提升海量倒排索引数据存储和查询性能的必要手段和研究热点。

目前，倒排索引压缩算法中被广泛研究和采用的是字对齐压缩算法，该类型算法又可以分为参照框架（Frame Of Reference，FOR）类型压缩（如：FOR、PFOR（Patched FOR）、OPT-P4D（OPTimzed PForDelta）等算法）和等字长（Fixed Word-Aligned，FWA）类型压缩（如：S9、S16、S8b 等）两类［6-7］。本文所研究的FWA 类型压缩算法在保证每个被压缩整数位宽小于其填充模式的限制条件下，所采用的整数序列“贪心”划分策略将尽可能多的相邻整数存储在32q（q为正整数）位的机器字内。研究表明，FWA 类型算法的优势在于：1）在给定的机器字长内存储模式更加细化，可以缓解倒排链中异常数字导致的分块位宽的浪费问题；2）其压缩码字能够和搜索引擎系统的IO 缓存池的读写数据块对齐，可以避免读写磁盘压缩倒排索引数据时的跨数据块解压问题［4］。然而，现有FWA 类型算法的指示位和数据位是交错存储的，这使得解压过程必须对每个机器字进行指示位提取处理，从而制约了解压性能。此外，FWA 类型算法的相邻填充模式的可压缩整数个数是不连续的，在相邻整数差距较大、序列长度较短时，如果多压缩一个整数可能会导致下次存储模式存在严重的位宽损失问题，因此，现有FWA 类型算法采用的“贪心”分块划分策略无法达到最优的压缩率。实际上，在FWA 类型算法的存储模式限制下使最终的划分分块总数最少才能达到最优的压缩效果。如何选择有效的倒排链划分方法是提升FWA 类型算法压缩性能的关键。

针对传统FWA 类型算法中存在的码字信息交错存储和分块划分策略空间损失问题，本文研究FWA 类型算法压缩下的倒排链存储策略和分块划分和问题。首先，设计了一种指示位和数据位单独存储的新型FWA 类型压缩算法；然后，提出了一种基于有向无环图（Directed Acyclic Graph，DAG）描述的倒排链FWA 划分压缩方法——固定字对齐划分（Word-Aligned Partition，WAP）算法；之后，采用动态规划方法求解基于DAG 的最优划分问题；最后，通过仿真整数序列数据和文本检索会议（Text REtrieval Conference，TREC）GOV2索引数据对本文所提WAP 压缩算法进行实验分析。实验结果表明，本文所提基于DAG 的倒排链划分优化算法相较FWA 类型算法和FOR类型算法在压缩率和解压速度指标上有优势。

1 相关工作

倒排索引压缩算法中的字对齐压缩算法可以按照每次压缩的码字大小是否相等分为FOR类型算法和FWA类型算法。FOR 类型算法的主要思想是选取32q（q为正整数）个整数作为一个分块进行等位宽压缩，头部指示位中需要包含压缩分块的空间占用信息，只保证了数据位的码字末尾是字对齐的，如：FOR、PFOR 等算法［8-10］。FOR 类型算法的性能优势在于针对较长倒排链的压缩，在倒排链长度较短时其压缩率受异常值影响较大。OPT-P4D算法通过权衡分块内位宽和压缩异常值的开销，从而在不影响解压性能的条件下提升算法的压缩率［10］。

FWA 类型算法在给定的机器字长内存储模式更加细化，可以降低异常数导致的序列中其他整数压缩位宽的浪费。Anh等［11］提出的S9压缩算法使用4位作为指示位描述其余28个数据位，形成9 种可能的数据位存储模式。每种存储模式为每个被压缩的整数分配固定的位宽，但存在一定的比特位宽浪费。S9 算法在压缩过程中将尽可能多的相邻整数压缩在给定的32 位机器字长内，这实际上就是对整数序列的一种向左的“贪心”划分策略。解压阶段通过指示位所确定的存储模式来提取数据位存储的所有整数。当FWA 类型算法所剩的待压缩整数个数较少时会导致存储模式不匹配，此时存储模式的位宽浪费问题就比较明显。为了降低存储模式的位宽浪费，研究人员提出了具有更为丰富存储模式的FWA 类型算法，其中包括S16 算法以及Carryover-12、Slide、S8b、Slide8b、Carry8b 等算法［9，11-12］。FWA 类型算法中存储模式的可压缩整数个数和位宽的非连续性，以及整数序列分块划分的不合理性，使得整数序列分块内的异常值提升了块内其他整数的存储位宽［13］。

为了降低倒排链中的异常值给压缩算法带来的位宽浪费，研究人员提出了基于倒排链分块划分的优化压缩方法［14-15］。该类优化方法首先寻求最优的倒排链分块划分，然后在每个分块内部进行等位宽存储，同时保证连续的多个分块是字对齐的。针对FOR类型压缩算法，Silvestri等［14］提出的VSE（Vector of Splits Encoding）算法针对整个倒排链使用动态规划方法寻找最优分块划分，并采用再压缩技术提升算法的压缩率，形成VSE-R（VSE-Recoding）算法；该类算法难以构建字对齐的自索引结构，且采用的全局优化的计算代价太高，使索引构建的时间大大加长。Delbru 等［15］提出的AFOR（Adaptive Frame Of Reference）算法采用固定长度的滑动窗口方式来划分分块，且分块长度仅可取8、16、32 三种；该方法可以说是采用动态规划技术求解倒排链的局部最优划分来避免过高的计算代价。Brisaboa 等［16］提出的DACs（Directly Addressable Codes）算法使用了和VSE 算法相同的思想，但其分块内采用了与VByte（Variable Byte）算法类似的字节压缩方式，同时对不同长度的码字构建分层结构来实现随机访问的效果。Pibiri 等［17］提出的PEF（Partitioned Elias-Fano）和CEF（Clustered Elias-Fano）压缩算法也构建分层压缩结构，在划分时把整数序列视作有向无环图（DAG），并引入近似计算的方法完成整数序列的最优划分。针对FWA 类型压缩算法，Trotman 等［18］通过对倒排索引进行划分来提升S9 算法的压缩率，但是该方法未能深入分析FWA 类型算法的存储模式局限对最优划分结果的影响。

2 问题定义

假设L[0，n]（记为L）表示一个长度为n的严格递增的正整数序列（如：倒排链中的d-gap 或者freq序列），L[i]表示序列的第i个元素，L[i，j](0 ≤i≤j＜n)表示序列L的从位置i到位置j的分块。倒排链中的整数序列L的压缩是在分块上进行的，每个分块的位宽和长度是不同的，如何划分分块影响着倒排索引的压缩率。实际上，序列L[0，n]可以被视作一个有n个节点的有向无环图（DAG）G，其中每个节点vi(i∈[0，n-1])代表序列L中的一个数值，vn表示空节点。图G是一个完全图，即对任意i和j满足0 ≤i≤j＜n，就会存在一条边连接vi和vj，表示为(vi，vj)。这条边对应序列L中的一个划分分块L[i，j]，每条边的权重ω(vi，vj)=C(L[i，j-1])，C为对分块L[i，j-1]进行压缩的算法。此时，序列L的划分问题就转化成了在图G中规划一条从节点v0到vn的路径π。比如，路径（i0=0 且im=n）即对应了序列L的一种有效划分方案L[0，i1-1]L[i1，i2-1]…L[im-1，n-1]，其中m表示路径π包含的边的个数；记划分向量S={0，i1，i2，…，im-1}中的元素为每一个划分分块在序列L中的起始下标。

在DAG 理论的描述下，倒排链的最优划分问题就归约成为了一个单源最短路径（Single-Source Shortest-Path，SSSP）计算问题。如图1所示为含有5个文档号的DAG描述示意图（v0到v4，v5为空节点），其中每个节点代表一个d-gap，每条边代表一个分块的起止位置。边下面的数字表示压缩对应分块作为节点之间路径的代价E（位），由固定代价（本文算法为4位）加编码分块的位宽得出。虚线表示当前的最短路径，即当前倒排链的最优分块划分。图G中每条路径π都对应着一种可行的分块划分方案，而路径的权重之和就是倒排链中序列L压缩后的空间大小。所需要计算的就是在所有对序列L的划分向量中找出使得压缩空间开销|FWA(L，S)|=最小的向量S，即：

图1 倒排链划分的DAG描述示意图Fig.1 DAG description of inverted list partitioning

另外，本文在研究网页d-gap 整数序列分布情况和现有FWA 类型算法的基础上，为了降低FWA 类型算法在对小数字序列压缩时可压缩整数个数和位宽的非连续性，设计了一种64 位机器字对齐压缩算法，并结合最优划分技术实现压缩性能的提升，称之为固定字对齐划分（WAP）算法。如表1 所示，该算法设计了16种64位的存储模式p，每种存储模式可压缩k个整数，分块内每个整数的位宽b是不变的。该算法将指示位和数据位单独存储，可以保证较高的解压性能，即将4 位的指示区单独存储于整数序列的压缩码字头部，并硬编码实现16种64位数据区的存储模式。另外，将部分存储模式的损失位加入该模式的其他位宽中，这样该存储模式的位宽将是不固定的，在不影响算法的划分优化性能的情况下可以提升算法的压缩率。因为WAP 算法的位宽从1～10 是连续的，所以这一算法适合处理连续的小数字序列压缩。

表1 WAP压缩算法的存储模式Tab.1 Storage modes of WAP compression algorithm

对于拟采用WAP算法压缩的倒排索引，给定划分向量S，假设bi是可以表示分块L[i，j-1]中最大元素的最少位数，即假设ki是分块L[i，j-1]中的元素个数，即ki=j-i，则0 ＜ki≤K′，其中K′为最大分块长度。此外，如果采用WAP 算法的某一个存储模式p(0 ≤p＜P′)（P′是存储模式的个数）对分块L[i，j-1]进行压缩，那么求解SSSP 问题还必须满足存储模式的3 个隐含限制条件：bi≤bwidth[p]、ki=gsize[p]和ki*bwidth[p]=机器字长。

3 动态规划求解方法

本章利用动态规划方法来求解式（1）所定义的DAG 的SSSP问题。首先把图G中所有节点的最优路径代价E初始化为+∞，然后从v0到vn迭代，当到达节点vj(0 ≤j＜n)时，所有从v0到vi(i＜j)之间的最优路径代价E[i]已经计算。从v0到vj之间的新的路径代价E'[j]为从v0到vi的最优路径代价E[i]与从vi到vj之间的最优路径代价C(L[i，j-1])之和。优化过程需要根据WAP 算法存储模式的3 个限制条件寻找最优的节点(i*＜j)，并计算从到vj之间的新路径的代价C(L[i*，j-1])。当新计算的路径代价E[j]变小时，更新节点vj的代价E[j]，其转移状态定义如下：

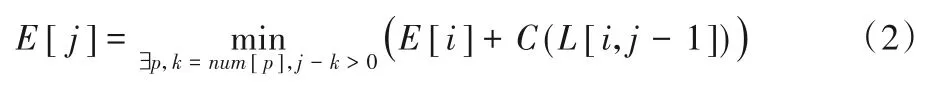
其中：对序列L，E[i]也指从节点v0到vi之间的子序列L[0：i-1]的最优压缩开销；C(L[i，j-1])是子序列L[i：j-1]的压缩开销。

算法1 给出了动态规划求解的最优划分问题的伪码。令E[1]=0作为循环的起始值，因为这代表空序列的编码开销。当对式（2）循环求解后，E[n+1]的值就是整个序列L的最优划分。算法1 中，首先设E[1]=0，然后从左至右计算E的每一种情况（第2）～12）行）。每一次E[j]的计算中，通过确定某个下标i*＜j使得E[i*]+C(L[i，j-1])的值最小。对于WAP 压缩算法，每个分块的压缩开销为C(L[i，j-1])=1。这一位置i*是通过对位于j-K′和j-1 之间的所有有效位置（需要从WAP算法的P′个有效位置中确定最优存储模式的下标p*）进行计算得到的（第4）～12）行）。在算法执行过程中，还需要将每次计算的存储模式下标p*保存在存储模式数组P中，并将以当前节点vj为右边界的分块的左边界i*存储在划分节点数组V中（第11）～12）行）。在计算结束后，E[n+1]表示压缩序列L的分块个数。此时，就可以通过数组V中的值来恢复最优划分向量，即从下标n+1 逆向获得值V[n+1]、V[V[n+1]]、V[V[V[n+1]]]等（第13）～16）行）。

算法1 倒排链的最优分块划分算法。

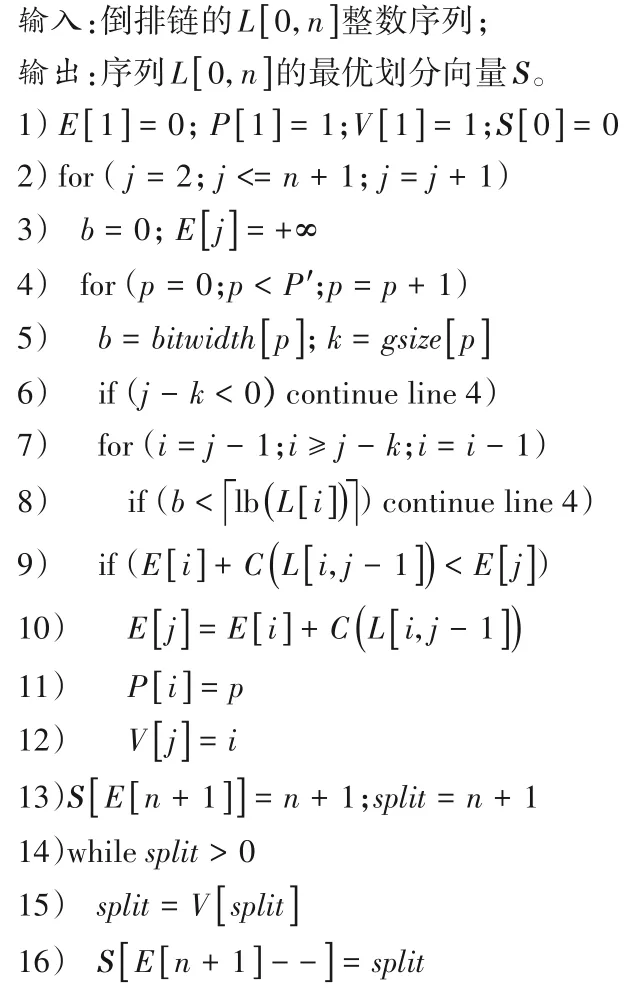
本文所提出的WAP 算法压缩过程的计算复杂度为O(n⋅P′⋅K′)。目前针对FOR 类型算法的优化工作中：OPT-P4D 压缩优化过程的计算复杂度为O(n⋅P′)，P′为算法所有可能的压缩模式个数；AFOR 压缩优化过程的计算复杂度为VSE 压缩优化的计算复杂度为O(n⋅K′)，不同算法的最大分块长度K′不同。因此，本文优化方法和上述两种方法具有类似的计算复杂度。WAP 压缩算法虽然因为压缩优化而降低了压缩速度，但是能够在保持解压速度的前提下明显提升压缩算法的压缩率。

4 实验测试与结果分析

实验部分通过仿真整数序列数据和TREC 网页索引数据对基于DAG 的FWA 类型优化算法进行性能测试。考虑到互联网网页索引数据的文档号是聚类分布的，因此实验采用聚类数据分布模型生成仿真测试数据［12］。假如需要生成的整数数组A[l，l+1，…，s]长度为f，当f＜10 时，按照均匀分布生成数据，即在给定整数大小区间内按照均匀分布生成f个递增整数数据；当f≥10 时，将整数数组分为两个子数组A[l，l+1，…，r]和A[r+1，r+2，…，s]（m按照某一策略选定）。这两个子数组又依据一定概率（0 ＜λ＜1）按照下面三种情况迭代：第一种情况子数组A[l，l+1，…，r]按照均匀分布生成，子数组A[r+1，r+2，…，s]按照聚类分布生成；第二种情况子数组A[l，l+1，…，r]按照聚类分布生成，子数组A[r+1，r+2，…，s]按照均匀分布生成；第三种情况子数组A[l，l+1，…，r]按照聚类分布生成，子数组A[r+1，r+2，…，s]也按照聚类分布生成。这三种情况的概率λ分布为0 ＜λ＜0.25、0.25 ≤λ＜0.5 和0.5 ≤λ＜1。这样，迭代的过程都是小范围的短整数序列，从而实现了数据的聚类分布。

TREC 网页压缩性能测试需要在搜索引擎索引平台上进行。本文利用GOV2 网页标准数据集构建基于文档号排序的倒排索引。GOV2 数据集是TREC 组织提供的基于2004 年互联网上.gov域名下的约2 520万个网页构成的数据集，未压缩状态下的大小为426 GB。该数据集作为2004—2006 年Terabyte Tracks任务的测试数据集，一般用于对搜索引擎系统架构的性能测试和评价。本文采用开源检索系统Terrier4.0平台构建GOV2 网页的倒排索引数据。首先，对网页数据进行预处理：网页数据集在去除超文本标记语言（HyperText Markup Language，HTML）标签后待索引的内容包括网页标题、正文与锚文本等内容；这些内容分别除去标准的英语停用词，并用Porter 词干分析器进行词干提取。然后，采用基于合并的索引构建法进行倒排索引的构建，默认压缩算法为Eliasγ。最后，采用索引转换方式生成各种压缩算法压缩的索引数据。本文仅考虑倒排信息中包含d-gap和freq的倒排文件。

为了测试WAP 算法的存储模式的关联性优势，实验对比算法包括S9、S16 和S8b 以及本文所提基于DAG 的划分优化（OPT）算法：OPT-S9、OPT-S16 和OPT-S8b。另外，对比实验还选取FOR 类型的OPT-P4D、AFOR 和VSE 三种优化算法。实验是在拥有Intel（R）Core（TM）双核i7-7500U、主频为2.70 GHz 和2.90 GHz、8 GB RAM 的处理器上完成。实验软件测试平台运行于版本为1.7.0_71 的Java 虚拟机之上。本实验采用压缩率、压缩速度和解压速度3 个指标评估算法的压缩性能，压缩率单位为bpi（每个整数占用比特位），压缩速度和解压速度单位为mis（每秒百万整数）指标［14］。压缩测试实验进行3 次并取平均值。本文所有的实现代码（包括索引结构、压缩算法和仿真平台等）可以访问GitHub（http：//github.com/deeper2/web-index-bench）来获取。

4.1 仿真数据压缩实验

本节采用仿真系统模拟的倒排链整数序列进行内存压缩测试。生成的随机测试数据的分布范围为［0，229）。生成较长整数序列数据共1 024 个，每个包含225个整数（也可以生成更多的整数，如228），因此连续整数之间的差值d-gap 为229-25=24，压缩数据平均至少需要4位，结果如表2所示。

由表2 可以看出，本文所提出的优化算法可以获得一定的压缩率提升，虽然压缩速度因计算最优划分向量而降低，但是作为搜索引擎查询过程重要的解压速度指标是基本保持不变的。从实验结果可以看出，本文所提出的基于动态规划求解最优整数序列最优划分的方法，在对解压速度没有明显影响的前提下能够提升FWA 类型算法的压缩率。此外，由于本文为了单独测试最优划分的效果，对于VSE 算法并没有考虑再压缩的情况（即VSE-R 算法），可以看出WAP优化算法相较于AFOR 和VSE 压缩算法也有一定的优势。这是因为WAP算法对于较长的d-gap序列具有较多的存储模式，而且存储模式的指示位开销较少，所以对于符合网页聚集特性的连续小数字整数序列，其压缩性能并不弱于AFOR和VSE算法。

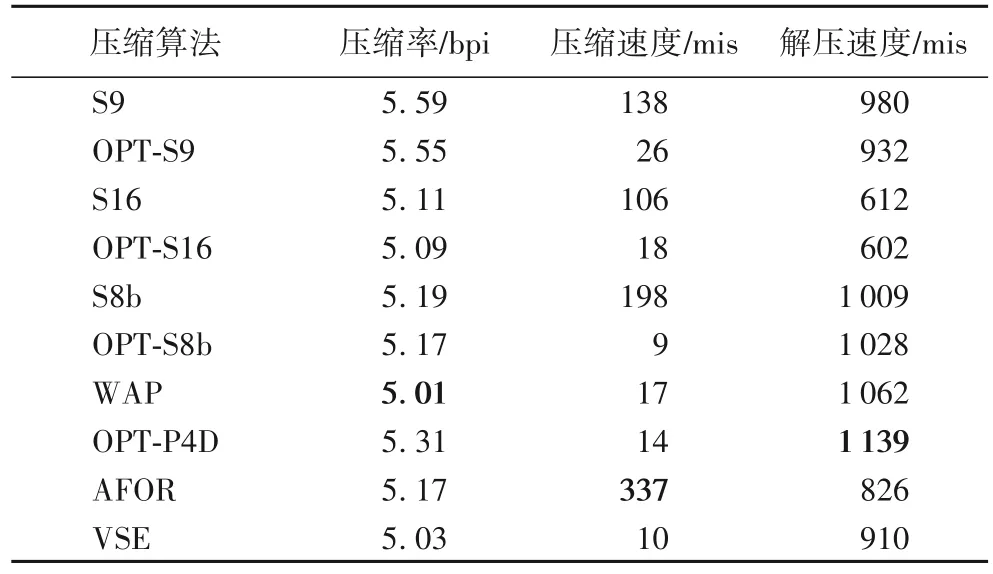
表2 聚类仿真数据上压缩算法的性能对比结果Tab.2 Performance comparison results of compression algorithms on clustering simulation data

4.2 TREC索引压缩实验

本节对由Terrier4.0索引系统生成的TREC GOV2网页索引数据格式转换，并采用新的压缩算法进行磁盘数据的压缩和解压性能测试，选择长度大于128 的倒排链以降低解压过程中频繁的解压函数调用开销，实验结果如表3所示。

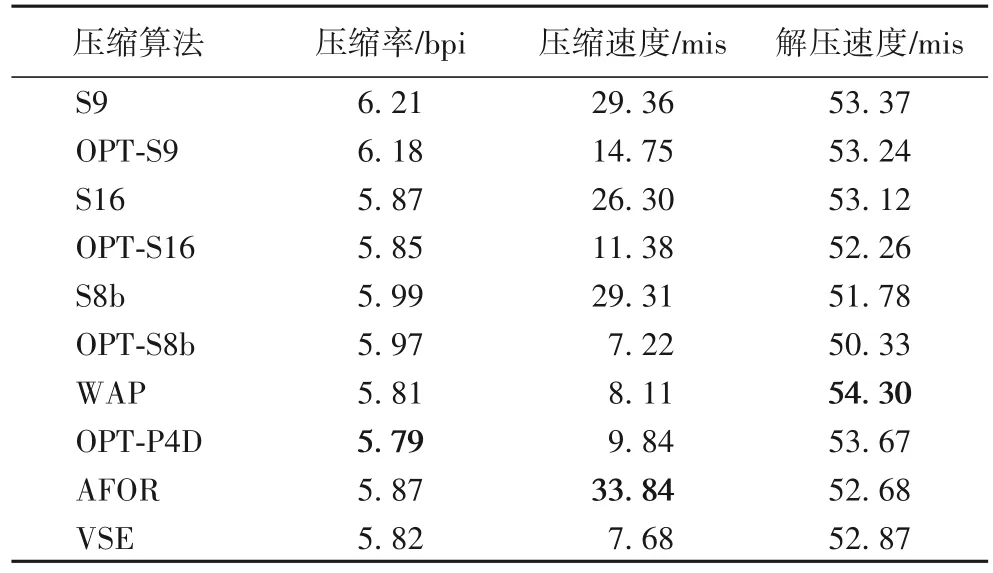
表3 TERC索引数据上压缩算法的性能对比结果Tab.3 Performance comparison results of compression algorithms on TREC index data

实验结果表明，本文所提出的划分优化能够提升FWA 类型算法的性能，而且重新设计的WAP 算法的压缩率达到最好的效果。各种划分优化压缩算法因为压缩过程需要进行动态规划算法求解，所以其压缩速度要低于传统非优化压缩算法。对于海量磁盘索引数据的解压性能基本比较稳定。考虑到FWA 类型算法的存储模式仅有16 种，AFOR 算法的存储模式有96种，VSE算法的存储模式有256种，而压缩算法的实现代码量和其存储模式的硬编码成正比。因此，如果为FWA 类型算法增加有效的存储模式，并辅以VSE 算法所采用的格式重排技术，可以预计其压缩率和解压速度会有一定程度的提升。

从表3和表2的实验结果可以发现，在仿真数据压缩实验中WAP 算法的压缩性能要明显优于OPT-S8b，但是在TREC索引压缩实验中WAP 算法的压缩性能仅略优于OPT-S8b。主要的原因是互联网相同主题网页的聚类效果不明显，而网页的采集过程有一定的随机性，导致倒排链的相邻文档号之间的差值d-gap较大，从而影响压缩算法的性能。而依据聚类模型生成的仿真数据的聚类效果较好，使得适合于处理小数字序列的WAP 算法的性能优势更加明显。从第3 章所述的WAP 算法的计算复杂度可以看出，如果大量的倒排链划分结果无法达到较长的分块，求解最优划分过程将使得K′较小，所以随着索引规模的增加采用WAP 或者OPT-S8b 算法划分出的分块长度可能相同（如：块长都为1 或者2），两种算法都会生成大量的较短分块，因此，WAP 和OPT-S8b 的压缩速度差距变小。

图2 是WAP 算法的存储模式的调用累积分布图。可以看出，倒排链压缩中调用的位宽较大的存储模式要多于仿真数据压缩，这进一步说明倒排链中待压缩整数序列中存在较多的大整数，而仿真数据中待压缩整数序列中生成的大整数较少。另外，从图2中可以看出，仿真数据和索引数据在WAP算法压缩过程中对于小数字分块的压缩次数要高于大数字分块的压缩。这也就是本文所提WAP 算法所设计的存储模式的优势，结合最优划分技术实现FWA 类型算法压缩率的提升。因此，如果按照TREC 网页的链接对倒排索引的文档号进行重排［19］，会使倒排链的d-gap 序列中的小数字增多，从而能够进一步体现WAP 压缩算法处理小数字的优势。另外，实验结果表明，在单个机器字长仅为固定的64 位时，设计更为精巧的存储模式对压缩率的提升空间有限。后续的研究工作应该针对FWA 类型算法进行可变字长的分块划分来增加有效的存储模式数量。

图2 WAP算法的存储模式的调用累积分布Fig.2 Distribution of calling accumulation of storage modes of WAP algorithm

5 结语

在搜索引擎系统的海量倒排索引压缩存储中，FWA 类型算法中存储模式的可压缩整数个数和位宽的非连续性，以及整数序列分块划分的不合理性，使得整数序列分块内的异常值提升了块内其他整数的存储位宽。本文设计了一种指示位和数据位单独存储的新型FWA 类型压缩算法，提出了一种基于DAG 描述的倒排链WAP 划分压缩算法，其核心是利用DAG进行倒排索引分块划分问题的描述，结合WAP算法的各种存储模式的位宽限制来确定最优划分问题的结构形式和递归定义，并利用动态规划技术求解基于DAG 的倒排链最优划分问题。本文对S9、S16 和S8b 三个FWA 类型算法及其优化算法以及WAP 算法进行了实现和分析。仿真和网页压缩实验验证了本文方法在压缩率和解压速度指标上较传统FWA类型算法和FOR类型算法的性能优势。

FWA 类型算法在压缩和解压时存在大量的存储模式切换开销，一些现有的倒排索引压缩算法如VSE 采用格式重排（Layout Permute）提升解压性能，即将其中相同存储模式的码字按照分块的位宽进行分类存储并批量处理。未来的研究工作可利用格式重排技术等优化实现方法来提高WAP 算法的解压性能，也可以采用再压缩或者文档重排技术进一步提升WAP算法的压缩率［19］。