地震作用下多层桥梁结构弹塑性分析
张 玥,薛 磊,杨宝刚,周 敉
(1.西安科技大学建筑与土木工程学院,陕西 西安 710054;2.长安大学桥梁与隧道陕西省重点实验室,陕西 西安 710054)
城市经济的高速发展及人口的迅速增加,使得我国的交通网络面临巨大的压力[1]。多层桥面的桥梁可以实现人车分流,解决由城市空间受限所导致的交通堵塞,在今后的一段时间里我国将会加大对多层桥梁建设的投入[2]。然而,近年来,国内外地震频发,由地震导致的建筑结构发生破坏的实例已屡见不鲜[3-6],再加上国内外对于多层桥梁结构的抗震设计可借鉴的资料十分有限[7-12],尚无成熟的理论提供参考,进行多层桥梁结构的动力分析就显得尤为迫切。
多层桥梁的桥墩受力具有多样性及复杂性,其塑性铰的出现位置及时间与单柱墩有很大的差距,我国的《公路桥梁抗震设计规范》(JTG/T 2231-01—2020)[13]及《城市桥梁抗震设计规范》(CJJ 166—2011)[14]中仅给出了单层桥梁的桥墩塑性铰可能出现的位置,对于多层桥梁的桥墩并无说明。基于此,笔者以某双层三跨及三层三跨混凝土箱型简支桥梁为背景,采用增量动力的分析方法,给出多层桥梁桥墩塑性铰的产生机制,以期充实桥梁抗震设计理论,完善抗震规范。
1 工程背景
以某双层三跨及三层三跨混凝土箱型简支桥梁为背景,双层桥梁的总体布置图及断面图如图1所示。主梁断面为单箱三室截面,桥墩采用直径为1.3 m的框架式桥墩,基础采用直径为1.5 m的桩基础;三层桥梁的总体布置图及断面图如图2所示。上层桥与中层桥主梁为单箱四室截面,底层桥主梁为单箱三室截面;桥墩为2×1.3 m的框架式桥墩,桩基础呈三角形分布,直径为1.3 m。桥墩和基础纵筋均为HRB335级钢筋,支座采用板式橡胶支座,型号为:GYZ550×110。

图1 双层桥梁示意图Fig.1 Diagram of double-deck bridge

图2 三层桥梁示意图Fig.2 Diagram of the three-story bridge
2 有限元模型
2.1 模型建立
地震响应提取第二跨的计算结果,建模时在计算模型第二跨的左右末端各加一联作为边界条件,且在临联结构上施加边跨荷载,考虑相邻结构和边界条件的影响。采用Sap2000中的桥梁模块分别建立4墩3跨的两种桥梁模型,模型的主梁、桥墩、系梁、承台及桩基础均采用梁单元模拟,桥面铺装采用面荷载模拟,采用双线性的恢复力模型模拟板式橡胶支座,滑动前的竖向刚度为5.94×106kN/m,剪切刚度为3 564 kN/m。场地类别为II类,特征周期为0.35 s。基础长度为30 m,采用分层土弹簧模拟桩土相互作用,每2 m施加一个土弹簧,弹簧刚度根据我国规范的“m”法计算,其中m动=2m静。有限元模型见图3所示。

图3 有限元模型Fig.3 Finite element model
2.2 地震动的输入
合适的地震记录对于增量动力分析尤为重要,根据我国《建筑抗震设计规范》(GB50011—2010)[15]的选波规定,选取符合条件的4条天然地震波,再加上规范反应谱拟合的一条人工合成地震波,共计5条地震波,地震波信息见表1所示。

表1 地震波信息Table 1 Seismic wave information
在地震动调幅的过程中,地震动幅值由0.1g增加到1.4g,增加步长取0.1g。调整方式如下:
(1)

3 关键截面的弯矩曲率分析
截面的弯矩-曲率分析是评价截面抗震性能的重要手段之一。为方便记录,在描述关键截面的弯矩-曲率分析时采用截面编号的形式进行记录,截面编号示意图如图4所示。恒载作用下,双层及三层桥梁的弯矩曲率分析数值如表2、表3所示。

图4 截面编号示意图Fig.4 Schematic diagram of section number

表2 双层桥梁弯矩-曲率分析数值

表3 三层桥梁弯矩-曲率分析数值
4 多条地震波下的IDA曲线
增量动力分析最重要的一步就是选取合适的地震动强度参数,常见的地震动强度指标有地震峰值加速度、地震峰值速度、结构第一个周期振型与阻尼对应的反应谱加速度值和结构的折减系数等[16-18]。地震动强度参数选取越合适,结构性能指标的偏差就越小,分析难度会下降。传统的地面峰值加速度PGA能够直接、有效的反映地震动的特性,选择PGA作为地震动强度参数,选用曲率作为判断结构进入屈服及破坏的指标。
4.1 IDA分析的终止条件
笔者进行IDA分析是为了确定墩柱塑性铰的潜在位置,因此应保证所有可能出现的塑性铰均不能发生破坏,即塑性铰区的曲率不能大于极限曲率,一旦任一塑性铰截面的曲率大于极限曲率,IDA分析终止[19]。以双层桥梁结构的San Fernando波为例,绘制单条地震动下的IDA曲线,如图5所示。图5中的黑色实线表示相应截面极限曲率的数值,黑线与曲线相交,表明该截面已达到极限曲率。
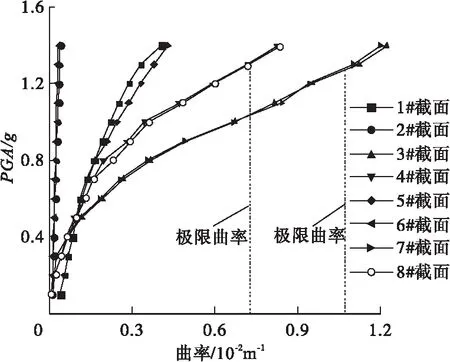
图5 双层桥梁San Fernando波的IDA曲线
由图5可知,1#、2#、5#及6#截面在PGA达到1.4g时,截面不会发生破坏;当PGA超过1.2g后,3#及7#截面的曲率已经超过极限曲率,截面已经发生破坏;当PGA超过1.3g后,4#及8#截面的曲率会超过极限曲率。以3#及7#截面达到极限曲率时所对应的PGA作为IDA分析的终止条件,即PGA为1.2g时,IDA分析终止。
同理,可以给出双层及三层桥梁结构在其余地震动分析时的终止条件,如表4所示。其中,San Fernando 地震波中的三层桥梁没有确定终止条件,这是因为PGA达到1.4g时,截面并未达到极限曲率,已无必要再增大PGA,因此三层桥梁San Fernando地震波分析的终止条件暂不考虑。

表4 各地震波分析的终止条件
4.2 双层桥梁的IDA曲线
将所选取的5条地震波按照前述的方法,以0.1g为步长,严格执行前述的终止条件,绘制不同地震波时的IDA曲线,在IDA曲线中标明各个截面等效屈服曲率的位置,即可看出该曲率对应的PGA,若该截面已达到等效屈服曲率,则该截面出现塑性铰。将各个截面达到等效屈服曲率时所对应的地震峰值加速度的结果列于表5中。双层桥梁的桥墩左右为对称结构,鉴于篇幅有限,仅给出1~4#截面的IDA曲线,如图6所示。

表5 等效屈服曲率对应的地震峰值加速度Table 5 Earthquake peak acceleration corresponding to equivalent yield curvature

图6 关键截面的IDA曲线Fig.6 IDA curves of key sections
图6中未出现黑色虚线的表示截面的曲率并未达到等效屈服曲率。在1~8#截面中,达到等效屈服曲率的截面有1#、3#、4#、5#、7#及8#截面,也就是说这些截面均出现了塑性铰,而2#及6#截面基本不会出现塑性铰,按照出现塑性铰时PGA的大小,可初步得出塑性铰的产生顺序为底层桥墩底→底层桥墩顶→顶层桥墩顶。塑性铰的出现位置如图7所示。
4.3 三层桥梁的IDA曲线
根据同样的方法,给出多层桥梁结构的IDA曲线,三层桥梁的桥墩左右为对称结构,仅给出1~6#截面的IDA曲线,如图8所示。

图7 双层桥梁的桥墩塑性铰的出现位置


图8 三层桥梁的IDA曲线Fig.8 IDA curve of the three-story bridge
将各个截面达到等效屈服曲率所对应的PGA结果列于表6。

表6 等效屈服曲率对应的地震峰值加速度Table 6 Earthquake peak acceleration corresponding to equivalent yield curvature
在1~12#截面中,达到等效屈服曲率的截面有1#、3#、5#、6#、7#、9#、11#及12#截面,不同的地震波,激发的塑性铰的个数稍有差异,但变化不大,塑性铰出现的位置有1#、3#、5#、6#、7#、9#、11#及12#截面,其余截面基本不会出现塑性铰,按照出现塑性铰时PGA的大小,可初步得出塑性铰的产生顺序为底层桥墩底→中间层桥墩顶→顶层桥墩顶→底层桥墩顶。塑性铰的出现位置如图9所示。
图9 三层桥梁的桥墩塑性铰的出现位置
5 塑性铰位置的比较
对于单层带有盖梁的双柱墩桥梁,抗震规范中已给出了塑性铰的出现位置,笔者又同时给出了双层桥梁及三层桥梁桥墩塑性铰的出现位置,如图10所示。

图10 不同层数桥梁桥墩塑性铰位置的比较
对于单层桥梁,塑性铰常常出现在墩顶和墩底位置;对于双层桥梁,塑性铰的出现位置有顶层桥的墩顶位置,底层桥的墩顶和墩底,而顶层桥的墩底位置不会出现塑性铰;对于三层桥梁,塑性铰的出现位置有顶层桥的墩顶,中间层桥的墩顶,底层桥的墩顶和墩底位置,而顶层桥和中间层桥的墩底位置不会出现塑性铰。双层及三层桥梁往往底部的塑性铰较易产生。
从前述的三种桥型来看,塑性铰的出现位置有较大的差异,但同时也有一定的规律可言。对于桥梁结构而言,最底层的桥墩底部会出现塑性铰,其余层墩底不出现塑性铰,各层的墩顶均会出现塑性铰,在进行延性抗震设计时,可以在这些塑性铰的三潜在位置设置抗震措施。
6 结 论
(1)对于双层桥梁结构,塑性铰可能出现在底层桥的墩底和墩顶、顶层桥的墩顶位置,塑性铰的产生顺序为底层桥墩底→底层桥墩顶→顶层桥墩顶;对于三层桥梁结构,塑性铰可能出现在底层桥的墩顶和墩底、中间层桥的墩顶、顶层桥的墩顶位置,产生顺序为底层桥墩底→中间层桥墩顶→顶层桥墩顶→底层桥墩顶。
(2)对于多层桥梁结构而言,最底层的桥墩底部会出现塑性铰,其余层墩底不出现塑性铰,各层的墩顶均会出现塑性铰。

