基于有限时间一致性的微网分布式二次控制

马秀娟，李范，赵玫，张华强

(哈尔滨工业大学(威海) 新能源学院，山东 威海 264200)

0 引 言

随着分布式发电在电力系统中的渗透率不断提高，由分布式电源(distributed generation，DG)、负荷、储能以及控制装置汇集而成的微电网备受关注[1-3]。当微电网运行于孤岛模式，分布式电源通常采用下垂控制，但下垂控制易受到线路阻抗特性、拓扑结构等因素的影响，使功率按比例分配效果不佳，且会导致频率与电压存在偏差，影响系统的稳定性。学者们针对下垂控制进行改进[4-8]，文献[5-6]增加微分和积分项自适应调节下垂系数以提高功率分配的精确度，但会影响系统电压水平。文献[7-8]引入自适应虚拟阻抗，实现了功率的解耦控制，提高了无功功率分配的精度。

上述研究是针对微电网一次控制进行改进，但无法同时满足频率、电压的无静差控制以及功率按比例分配的控制目标，进而引入微电网二次控制策略。微电网二次控制包括集中式和分布式两种。传统的微网二次控制主要是集中式控制，利用中央控制器收集交换每一个DG的电气信息，这需要复杂的双向通信网络，易发生单点故障，降低了系统的可靠性[9-10]。为克服集中式控制的弊端，基于多智能体系统(multi-agent system，MAS)的分布式控制被广泛应用于微电网的二次控制中[11-16]。基于多智能体理论的微电网分布式控制结构中将每一个DG看成一个智能体(Agent)，微电网可视为多智能体系统。分布式控制中每个DG只需与其相邻的DG交换信息达到控制目标，通信网络简单，能有效地避免单点故障，可靠性较高。文献[12]通过将获取的电压和频率的平均值与系统参考值的误差信息传给每一个对应的一次控制器来弥补频率与电压的偏差，与采用集中式控制器来收集系统的全局信息的方法类似，通信结构复杂。文献[13-14]通过反馈线性化的方法，将微电网的二次控制中频率、电压调节问题转化为多智能体系统跟踪同步问题，实现了在固定或时变的通信方式下频率与电压的调整及有功功率的按比例分配。文献[15]提出了基于多智能体一致性算法的频率、电压恢复控制，但未考虑线路阻抗不匹配对电压与频率恢复的影响。文献[16]采用多智能体动态平均一致性算法获取频率和电压的平均量实现了对频率与电压的调节，但在切换拓扑情况下有功功率按比例分配有误差。由于孤岛微电网可能会遭受突变的外部干扰，如DG的故障、负载变化等情况，因此加快收敛速度，实现有限时间内收敛具有重要意义。

受上述研究思路启发，本文提出了一种基于有限时间一致性的孤岛微电网分布式二次控制策略。一次控制采用下垂控制，二次控制结合多智能体理论与有限时间一致性协议并根据各DG与相邻DG交换的频率、电压及功率信息，设计了频率-有功功率控制器和电压-无功功率控制器，引入虚拟阻抗控制，根据无功功率的不匹配信息自适应调节虚拟阻抗，有效解决了线路阻抗不匹配问题下无功功率难以按比例分配的情况，实现有限时间内频率与电压无静差控制以及功率按比例分配，最后通过仿真验证所提出控制策略的有效性。

1.1 一次控制

图1为在孤岛运行模式下的第i个DG单元的控制结构框图，每个DG单元简化模型包含直流电源、DC/AC逆变器，LC滤波器、输出端以及控制器等部分。在d-q同步坐标系下建立每个DG单元的非线性动态模型，一次控制由电流控制回路、电压控制回路、功率控制回路组成[17]。

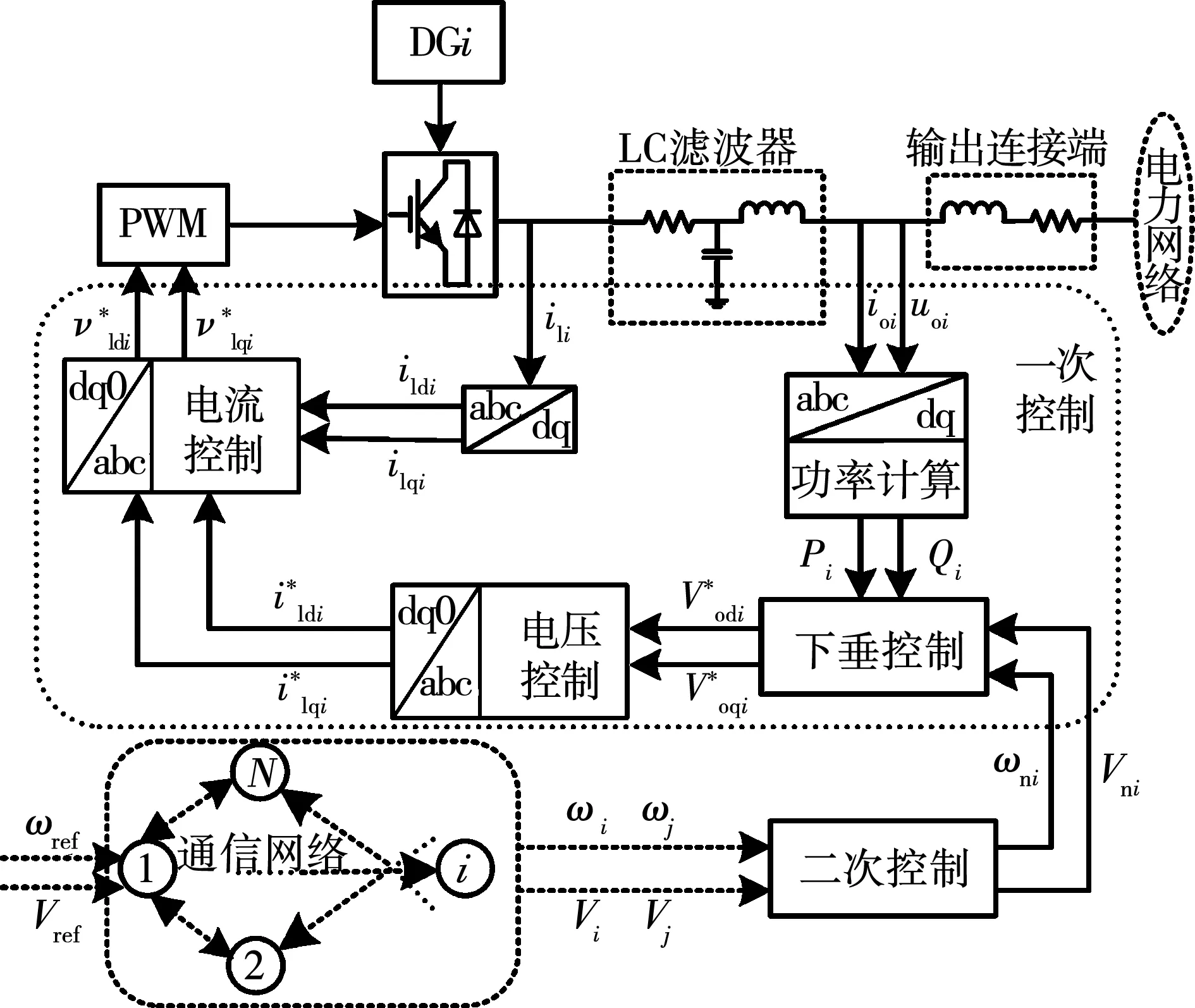
图1 DG控制结构框图Fig.1 Diagram of single DG control structure

一次控制对DG输出频率和电压的调节通常采用下垂控制，由于DG逆变器接口大多配置LC或LCL滤波器可以使其等效输出阻抗为感性，等效输出阻抗为感性的传统下垂控制方程为[18]

ωi=ωni-miPi，

(1)

Vi=Vni-niQi。

(2)

式中：ωi、ωni为DGi的输出频率和一次控制输出频率的参考值；Vi、Vni为第DGi输出电压和一次控制输出电压幅值的参考值；mi、ni为有功和无功的下垂系数；Pi和Qi为DGi输出有功功率和无功功率。

一次控制能够维持输出电压和频率的稳定，但其为有差调节。因此需要设计二次控制策略使系统输出频率ωi和电压Vi在有限时间实现无差调节以及DG间有功功率Pi和无功功率Qi的按比例分配。

1.2 多智能体协调分布式理论

若DG间存在通信连接，并将DG视为智能体通信网络中的节点，在分布式一致性控制中，节点状态xi仅取决于自身以及相邻节点的状态xj，最终达到所有节点状态的一致[19]。而当系统状态需要收敛到给定参考值xref，引入领导节点接收参考值信息通过与相邻节点进行信息交互后，使所有节点状态收敛至期望参考值，控制协议为

(3)

式中：xi表示节点i的状态量，用来代表微电网中频率、电压、功率等信息；ui(t)表示节点i的控制协议，若节点i可以从节点j接收信息，aij=1，否则，aij=0。bi(t)≥0表示第i个节点有参考输入。

为了提高收敛速度，改善系统的收敛性能，考虑有限时间控制内的分布式一致性控制，设计控制协议为

bi(t)φ2(sig(xi-xref)α)。

(4)

式中：00(∀x≠0)的连续奇函数，且对于常数Ck>0(k=1,2)在x=0附近有φk(x)=Ckx+o(x)。定义sigα(x)=sign(x)|x|α且sign(x)为符号函数。

1.3 二次控制

1.3.1 分布式频率-有功功率控制

分布式二次频率-有功控制的目标是设计合适的控制器在有限时间内补偿由一次控制导致的频率偏差，使系统内所有DG输出频率ωi在有限时间内恢复至频率参考值ωref并且维持之前输出有功功率Pi的按比例分配。

为使所有的DG输出频率同步到系统频率参考值ωref，在式(1)的基础上对其求导可得：

(5)

(6)

式中：ωni为分布式频率-有功功率控制器输入变量，包含δcωi和δcPi两部分，δcωi为输出频率辅助控制器，用来控制输出频率的同步，δcPi为有功功率辅助控制器，用来控制DG间输出有功功率的按比例分配。

假设微电网系统的通信网络是双向连通结构，即每个DG可以直接与其相邻的DG通信。根据每个DG自身以及与其直接相邻DG的输出频率信息，在协议(4)的基础上，设计输出频率辅助控制器δcωi如下：

bi(t)tanh(sig(ωi-ωref)α))。

(7)

式中：控制增益Cωi≥0；当且仅当DG有参考频率ωref输入时，bi(t)=1，反之为0。

对于多个并联DG组成的微电网，若各DG的频率相等，DG间的有功功率比例分配应满足：

m1P1=m2P2=…mnPn。

(8)

为实现式(8)的控制目标，令控制增益CPi≥0，并根据每个DG自身以及与其相邻直接通信的DG的输出有功功率，设计输出有功功率辅助控制器δcPi如下：

(9)

分布式二次频率-有功控制器δcωi和δcPi能够在有限时间使得所有DG的输出频率ωi同步到参考值ωref的同时满足系统中所有DG之间的有功功率按比例分配。

1.3.2 分布式电压-无功功率控制

分布式二次电压-无功控制的目标是使得所有DG的输出电压幅值Vi均恢复到电压参考值Vref并且实现无功功率Qi的按比例分配。在式(2)的基础上对其求导可得：

(10)

(11)

式中：Vni为分布式电压-无功功率控制器输入变量，包含δcVi和δcQi两部分；δcVi保证输出电压的同步，δcQi用来控制DG间输出无功功率的按比例分配。

根据各DG自身以及与其直接相邻通信的DG的输出电压信息，设计输出电压辅助控制器δcVi为：

bi(t)tanh(sig(Vi-Vref)α))。

(12)

与有功功率比例分配类似，DG间输出无功功率的分配应满足：

n1Q1=n2Q2=…=nnQn。

(13)

为实现式(13)的控制目标，令CQi≥0并根据每个DG自身以及与其相邻直接通信DG的输出无功功率信息，设计输出无功功率辅助控制器δcQi如下：

(14)

分布式二次电压-无功控制器δcVi和δcQi能够在有限时间内使微电网系统中所有DG的输出电压Vi同步到参考值Vref的同时实现系统中所有DG之间的无功功率按比例分配。

1.4 稳定性分析

以分布式二次电压-无功功率控制器为例进行分析，证明所设计的二次电压-无功控制器δcVi和δcQi能够在有限时间内使微电网系统中所有DG的输出电压Vi同步到参考值Vref的同时实现系统中所有DG之间的无功功率按比例分配。

首先，证明在控制器(14)的作用下可以在有限时间内实现无功功率的按比例分配。

1) 证明控制器(14)是全局渐进稳定的。

设niQi最终同步至nQ，令ζQi=niQi-nQ，那么可以将式(14)改写为

(15)

构造如下的Lyapunov函数，并对其求导，由于tanh(sig(·)α)是奇函数，根据文献[20]中引理2.1可得：

(16)

(17)

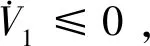
2)控制器(14)可以在有限时间内达到稳定。

根据函数tanh(x)为奇函数且其在零点时的泰勒展开式满足tanh(x)=x+o(x)，可将式(14)表示为

(18)

其中，令

当r1=r2=…rn=R，有

(19)

由式(19)可知，εαR=εσ+R，σ=R(a-1)，当R=2，σ=2(a-1)。因为0<α<1，因此σ<0。于是对于∀γ>0，∃t1>0，可以使得‖ζQi‖<γ，由于γ的任意性，因此ζQi对于所有t>t1是有界的。于是可以推出：

(20)

其次，证明在控制器(13)的作用下可以实现系统电压在有限时间内恢复至参考值，其证明过程与无功功率的比例分配证明过程类似，分布式二次频率-有功功率控制器的稳定性证明过程与上述证明过程相似。

2.1 线路阻抗不匹配对无功功率分配影响

图2为2台DG并联运行的等效电路模型，逆变器DGi的输出电压为Ei∠θi，θi为逆变器输出电压与公共点间的相位差，Zli为线路等效阻抗，ZDGi为逆变器等效输出阻抗，Zload为公共负载，公共耦合点电压为VPCC∠0°，DGi输出端电压与公共点电压之间的相角差为δi。

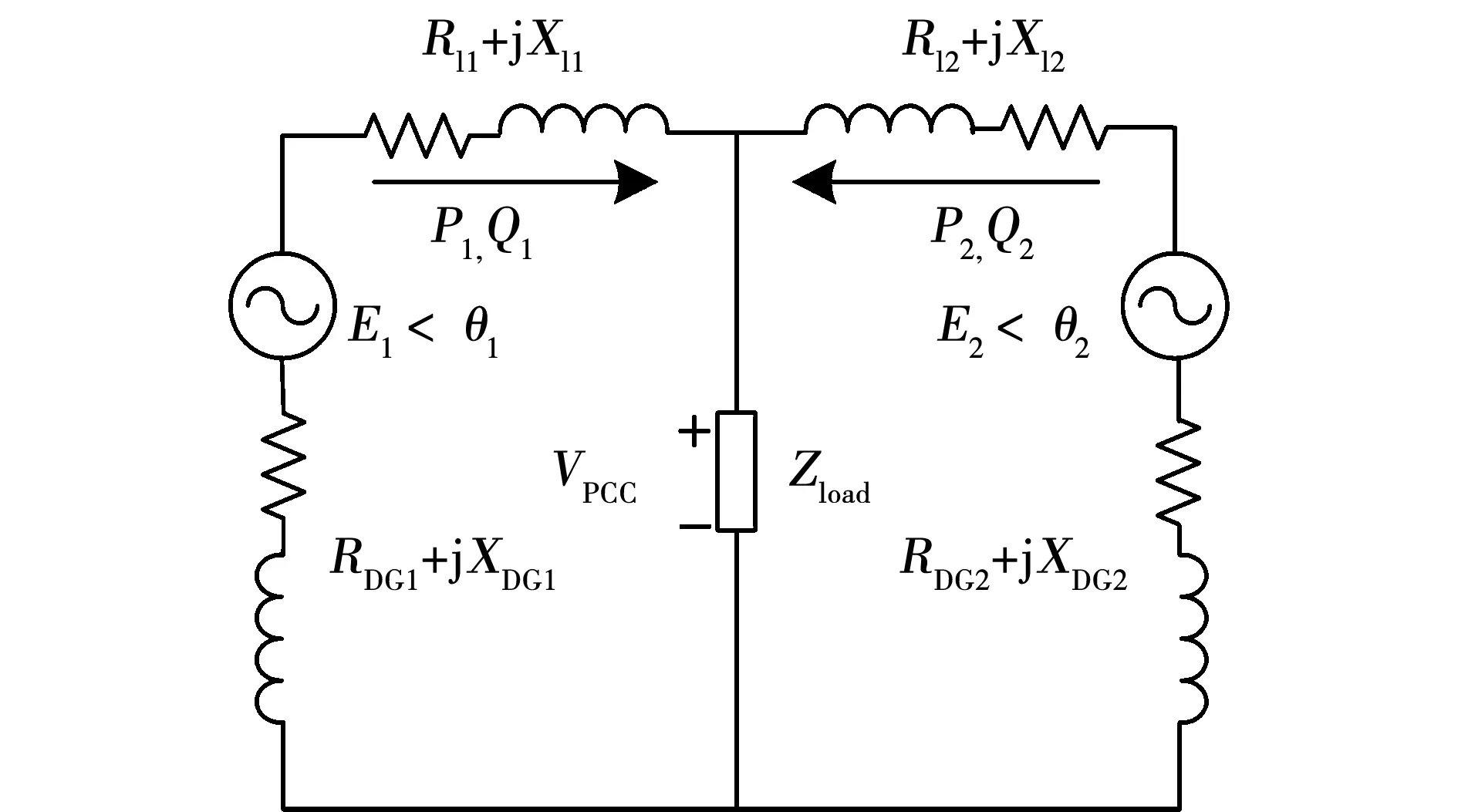
图2 两台DG并联等效模型Fig.2 Equivalent model of two DGs in parallel

根据图2可知逆变器输出的有功功率Pi和无功功率Qi可表示为[17]：

(21)

(22)

考虑在实际输出电压之间的相角差δi几乎为0，结合式(2)并改写式(22)，得到无功功率比niQi的表达式为

(23)

为满足无功功率的比例分配，应使线路等效电抗与其容量成反比，即

X1Q1=X2Q2=…=XnQn。

(24)

实际微网线路阻抗往往不匹配，式(24)很难满足导致其对无功功率按比例分配有影响，因此引入自适应虚拟阻抗控制并结合上文设计的辅助控制器来动态调整线路等效阻抗以实现无功功率的按比例分配。

2.2 基于自适应虚拟阻抗的无功功率控制

为实现无功功率Qi的按比例分配，应保证所设计无功功率辅助控制器中的niQi相同，根据DG自身以及与其相邻直接通信的DG输出无功功率信息得到的无功功率不匹配项δcQi，通过PI控制器对δcQi进行校正，得到虚拟阻抗校正项εcQi，用于更新虚拟阻抗进行自适应调节。图3为虚拟阻抗与虚拟电压控制框图。

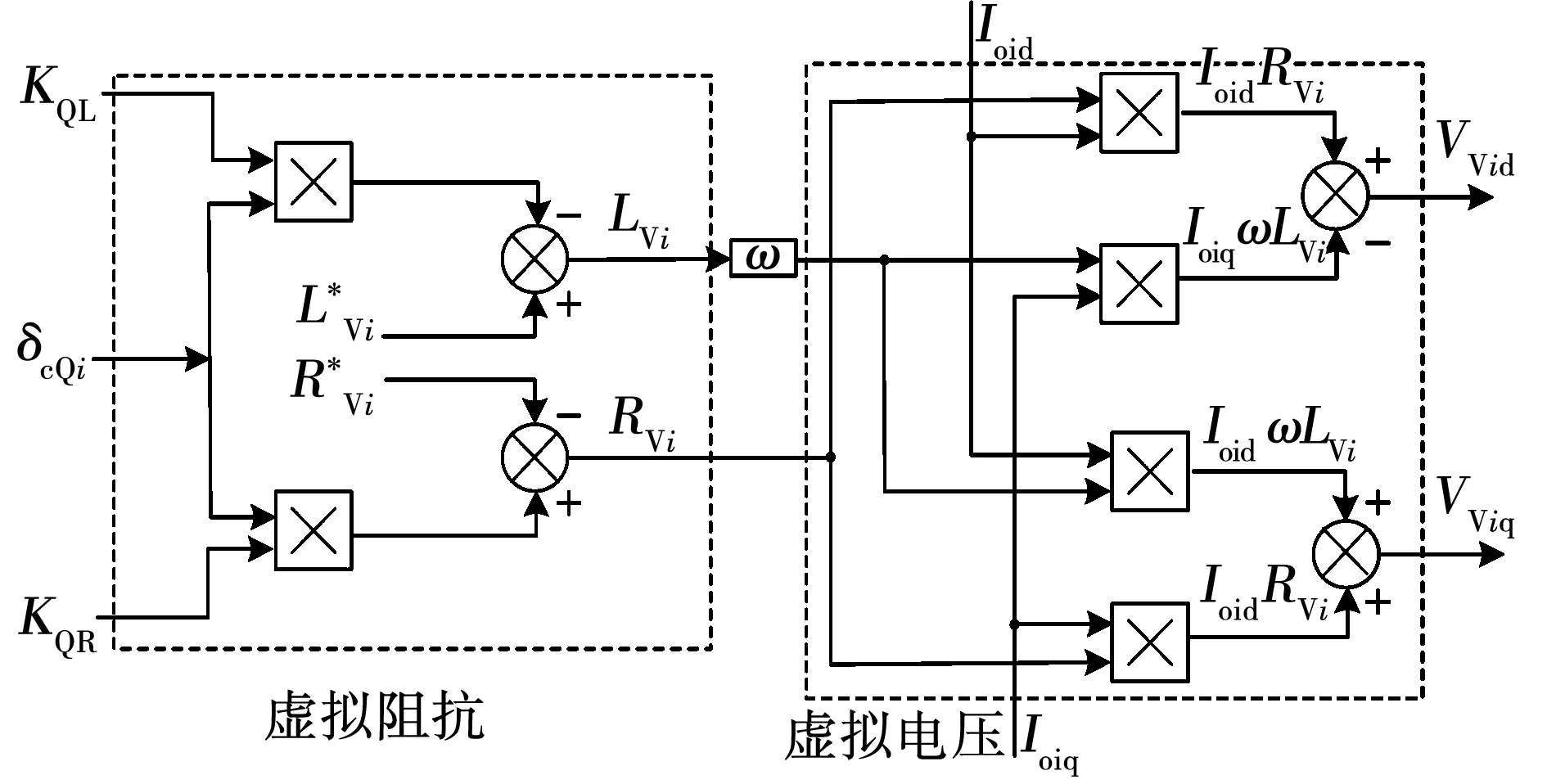
图3 虚拟阻抗与虚拟电压控制框图Fig.3 Virtual impedance and virtual voltage control

若DG间的无功功率分配未满足控制目标，可使DG间的虚拟阻抗利用下式自适应调节，即

(25)

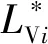
虚拟阻抗在d-q同步参考坐标系下所产生的虚拟压降为：

(26)

式中：VVid和VViq是无功功率经过二次控制后通过虚拟阻抗送往一次电压外环控制的电压校正值；Ioid和Ioiq为d-q坐标系下DG的输出电流分量。

从式(26)可以看出，虚拟阻抗的引入降低了有功功率和无功功率的耦合。将式(26)与电压下垂控制方程结合，式(2)可改写为

Vi=Vni-niQi+VVi。

(27)

此时假设第i个DG单元分配的无功功率比负荷所需要的无功功率多，根据所设计无功功率辅助控制器可知式(14)为负值，从而虚拟阻抗的修正量为负值，式(25)中的虚拟阻抗项增加，由于较大的等效阻抗的存在，减少了该DG单元的无功功率分配，因此，当无功功率的分配误差为0，实现无功功率的按比例分配，系统达到稳态，此过程不需要获得具体线路参数值。

结合上文内容，得到如图4所示的有限时间内微电网分布式二次控制框图。

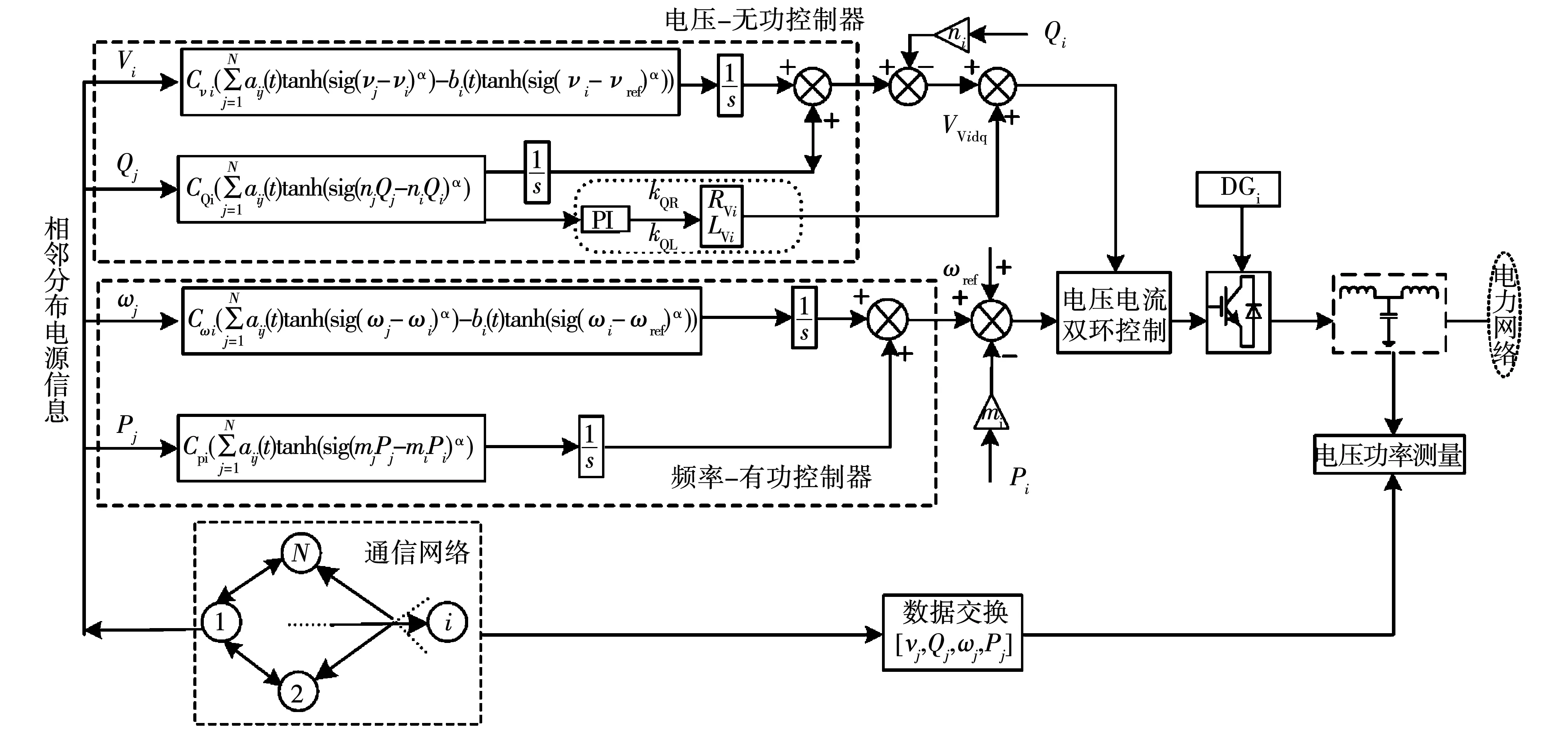
图4 有限时间内微电网分布式二次控制图Fig.4 Finite-time distributed secondary control in microgrid

搭建如图5所示的微电网系统仿真模型以验证所提分布式二次控制策略的有效性。令DG1可以直接获取电压与频率的参考值信息，电压参考值Vref为380 V，频率参考值fref为50 Hz。DG间通信拓扑如图6所示，微电网各个DG仿真参数与控制系统参数如表1和表2所示。

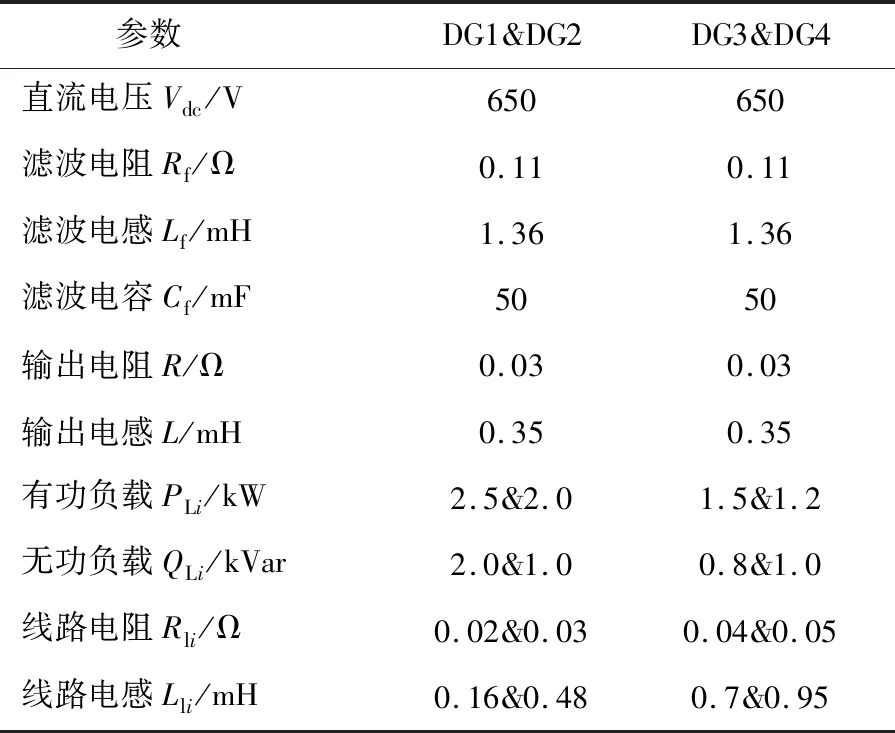
表1 微电网系统参数Table 1 Parameters for the test system and control

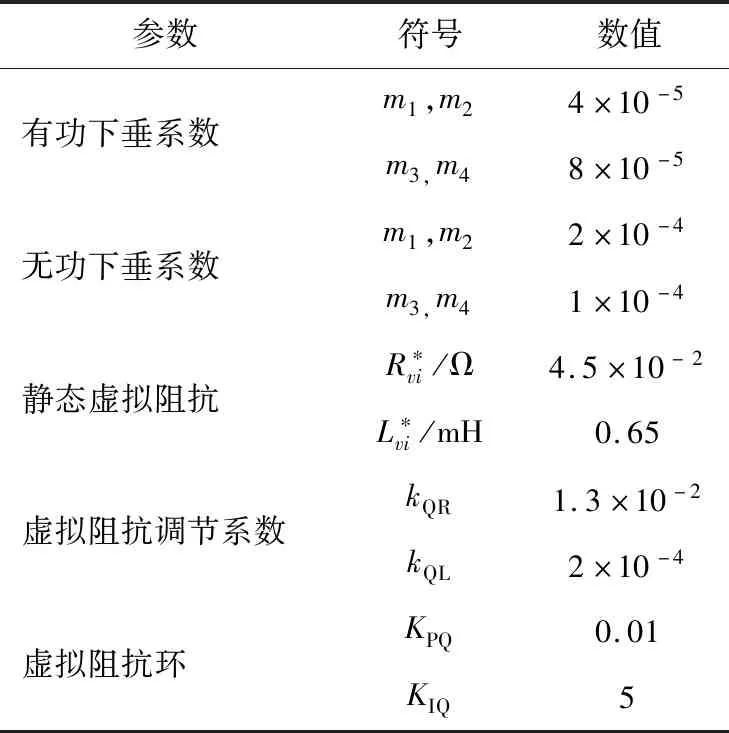
表2 控制系统参数Table 2 Parameters for control system

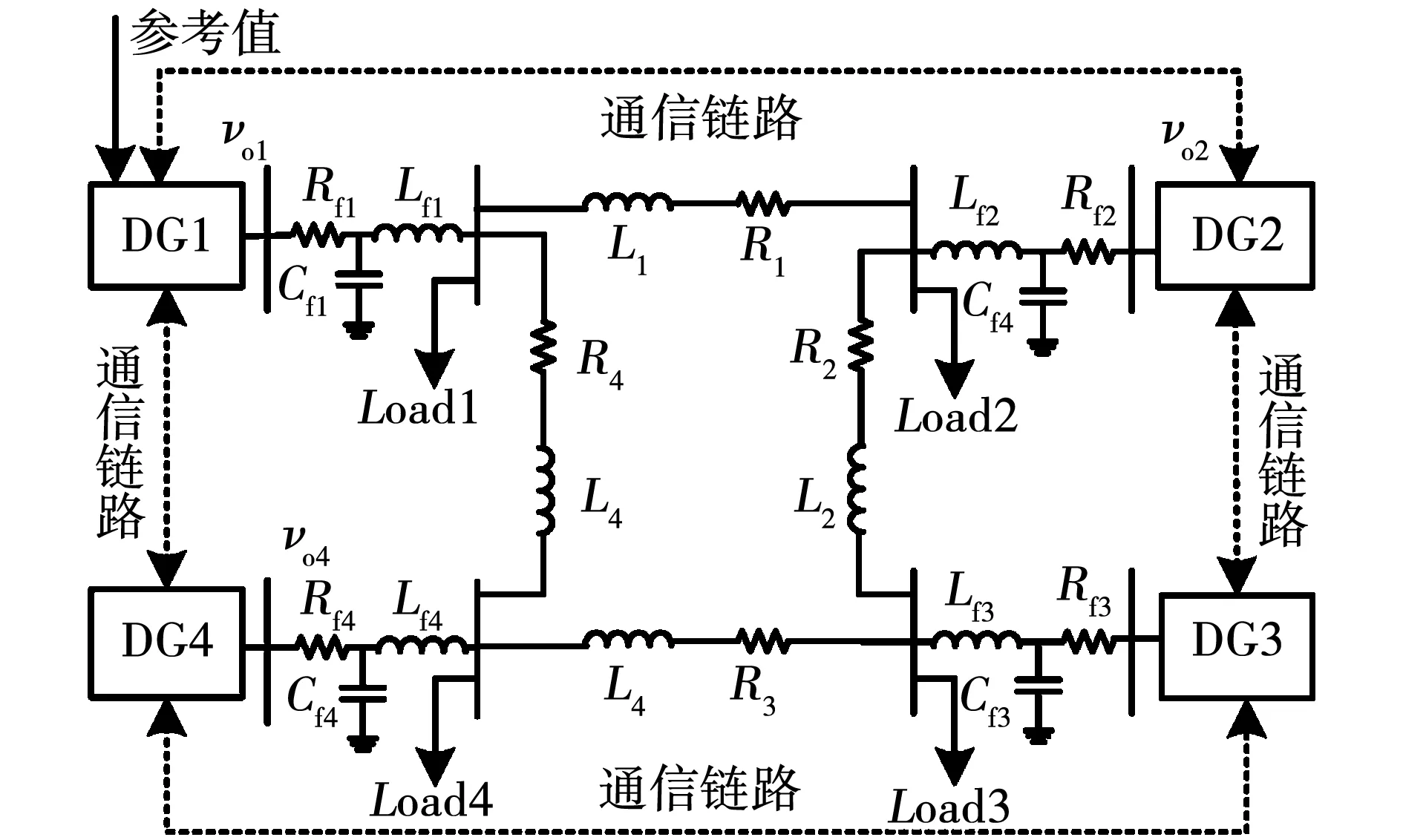
图5 4台DG单元组成的孤岛微电网系统Fig.5 Isolated microgrid system with four DGs

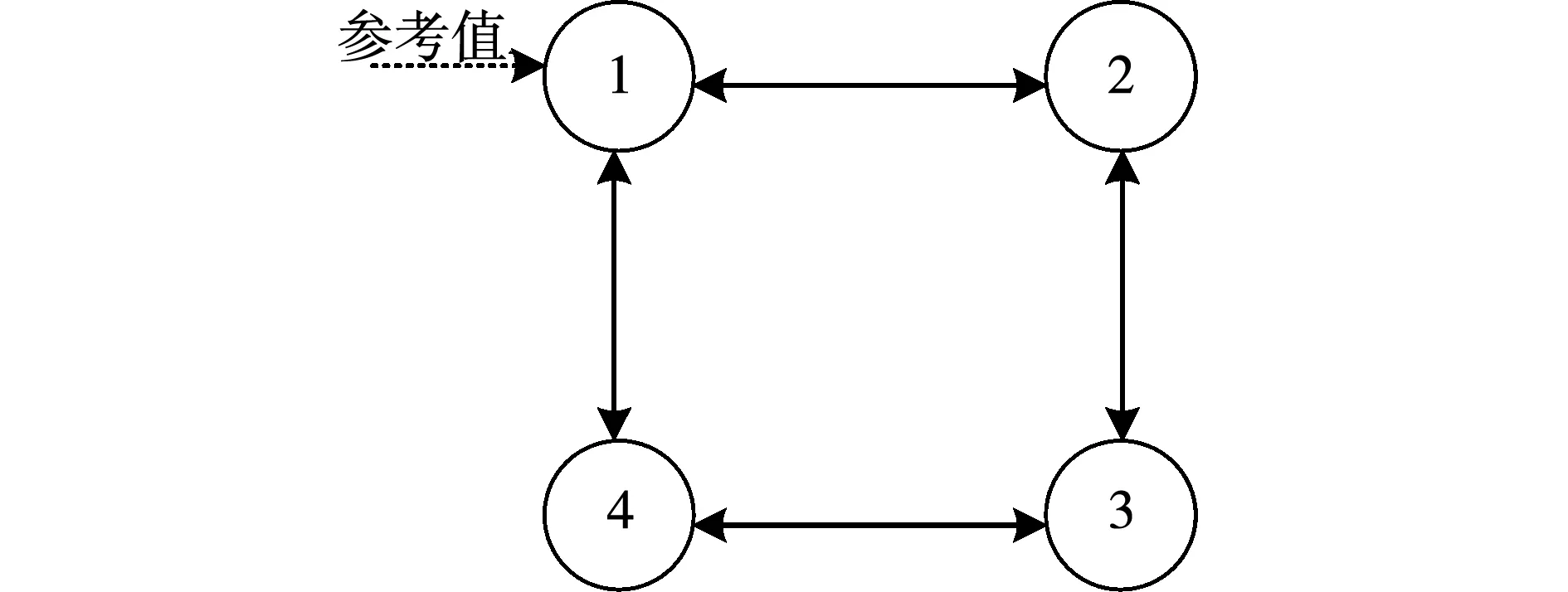
图6 DG间通信拓扑图Fig.6 Communication topology of DG units

3.1 算例1：负载变化

此情况下采用图6所示的通信拓扑，仿真分为4个阶段。阶段1：在t=0 s时微电网仅采用一次控制，且负载1在此时未接入系统，阶段2：在t=0.5 s时加入所提二次控制策略，阶段3：在t=1.5 s时，将负载3从电路中切除，阶段4：在t=2.5 s将负载1和3重新接入电路。负载变化情况下的仿真结果如图7所示。

从图7(a)和图7(b)可以看出，只有一次控制作用时，频率和电压与参考值有一定的偏差，在t=0.5 s加入二次控制策略后，经过短暂时间的过渡调节，电压和频率恢复至参考值，且无论负载如何变化，所提出的控制策略都可以将电压和频率恢复到参考值。从图7(c)和图7(d)可以看出，系统输出的功率会随着负载断开和接入相应的增加与减少，仍可在有限时间内完成有功功率和无功功率的按比例分配，维持系统的稳定。

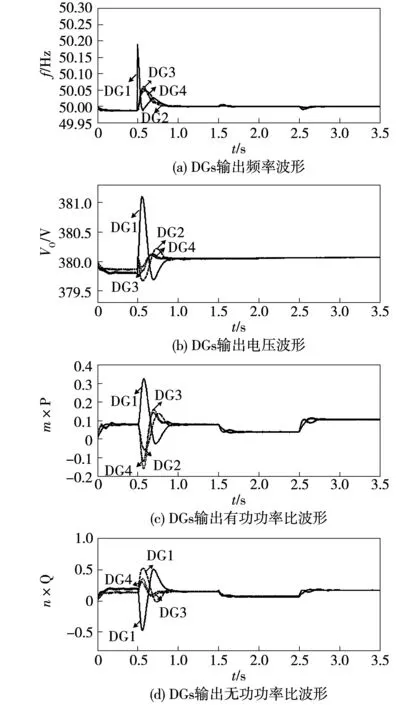
图7 负载变化仿真结果Fig.7 Performance evaluation under load perturbation

3.2 算例2：DG即插即用

即插即用是微电网在运行过程中需要满足的关键性能，设置DG2退出运行相当于中断与DG2相连的所有通信链路，此时通信拓扑变化为图8所示结构。仿真前两阶段与算例1相同，4个负载均接入系统，阶段3：DG2在t=1.5 s时退出运行；阶段4：DG2在t=2.5 s时重新接入系统。即插即用仿真结果如图9所示。

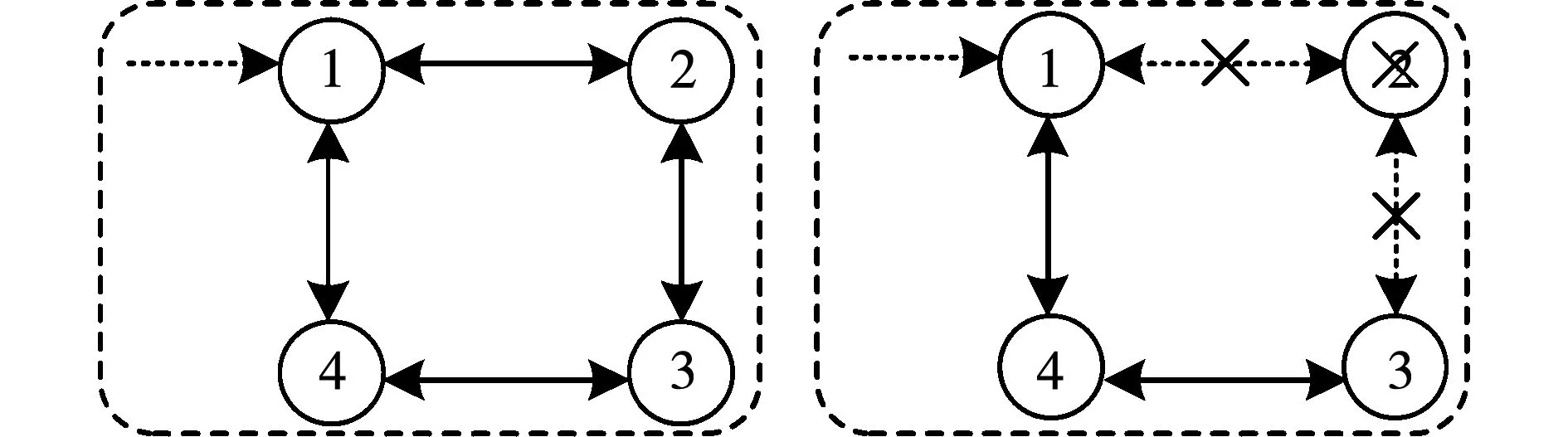
图8 DG即插即用特性通信拓扑Fig.8 Communication topology of DGs under plug and play operation

从图9可以看出，DG2在退出运行之前，系统经过调节后已达到稳定状态。当t=1.5 s，DG2从系统中退出运行时，DG2所输出的有功功率和无功功率缓慢的减至零，其他的3个DG在所提控制策略的作用下，产生更多的功率以补偿之前由DG2退出运行对功率分配的影响，仍可实现按比例分配新状态，DG2在当t=2.5 s时再次接入系统后，系统中的所有DG经过短暂协调控制，再次实现了功率的按比例分配，该功率分配状态与DG2退出运行前的分配状态相同，如图9(c)和图9(d)所示。因此针对DG2投切运行情况，除了某些瞬变外所提出的控制策略仍具有功率按比例分配以及频率和电压的恢复功能，且满足系统即插即用的性能要求。

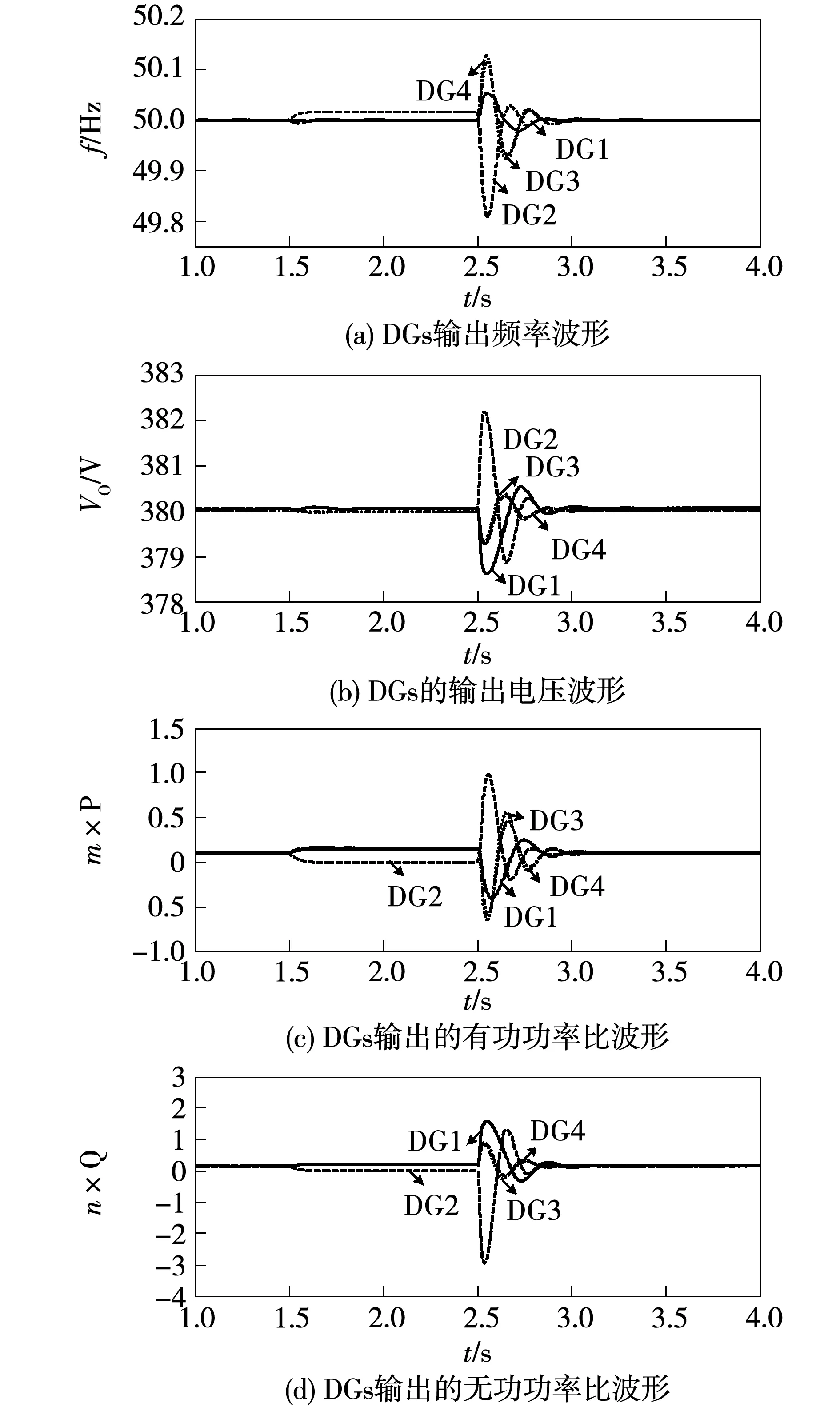
图9 即插即用性能仿真结果Fig.9 Performance evaluation under plug and play

3.3 算例3：控制策略对比分析

将本文所提基于有限时间一致性控制策略与基于传统渐进一致性控制策略进行对比，微电网系统参数设置参照表1，采用图6所示的通信拓扑，分两个阶段进行仿真。阶段1：在t=0 s时微电网仅采用一次控制且4个负载均接入系统；阶段2：在t=1 s时加入二次控制策略，以DG1为例的有功功率和无功功率的功率比对比曲线如图10所示。从图10知，在t=1 s加入二次控制策略后，基于传统渐进一致性控制策略经过0.7 s和0.6 s内达到有功功率和无功功率按比例分配的控制目标，而本文所提控制策略后分别经过在0.4 s内和0.3 s内实现有功功率和无功功率比例分配的控制目标，由此可见本文所提控制策略不仅可以实现功率按比例分配的要求，还加快了系统的收敛过程。

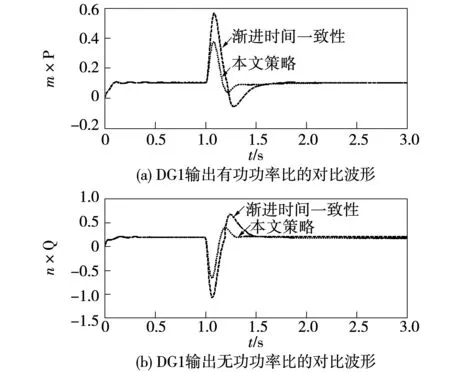
图10 DG1输出功率比的对比波形Fig.10 Output power ratios comparison waveforms of DG1

为实现孤岛微电网中多个分布式电源并联功率的按比例分配以及频率、电压的恢复控制目标，提出了一种基于有限时间一致性的微电网分布式协同控制策略，得出结论如下：

1)根据多智能体理论设计了分布式二次控制器，同时采用相关理论证明了所提策略的稳定性。所设计控制器中各DG单元仅需获得相邻DG的频率、电压及功率信息，可实现对频率、电压的恢复控制，避免对全局信息的依赖，可靠性较高。

2)研究了线路阻抗不匹配情况下的无功功率比例分配问题，引入虚拟阻抗控制，根据无功功率的不匹配信息得到的虚拟阻抗修正项自适应调整等效阻抗的大小，实现无功功率的按比例分配。

3) 在理论分析的基础上构建了微电网仿真模型，验证了所提控制策略的有效性且满足系统即插即用要求，增加了系统的灵活性。