数字自适应滤波器的性能退化规律

刘亚静，段超，李海东

(北京交通大学 电气工程学院，北京 100044)

0 引 言

基于SOGI的自适应滤波器，广泛应用于电网电量测量[1-3]、电机位置、速度检测与估计[4-9]等场合。目前，使用锁频环(FLL)来实现频率自适应算法是一种较为普遍的方法[1-6,8-9]。

在电网同步领域，基于SOGI的自适应滤波器主要用来提取电网电压中的正负序分量[1-3]。其中文献[1]采用MSOGI-FLL，在电网电压三相不对称或畸变的情况下，能够快速准确地提取电网电压的正负序分量和其他特定次谐波分量。

在PMSM的无位置传感控制领域，文献[4-5]分别将基于SOGI的频率自适应滤波器应用到基于电动势的位置观测器和模糊滑模观测器来消除谐波误差；文献[6]提出了一种复合SOGI-FLL用于PMSM的转子位置与转速估计；文献[7]将两个SOGI的组合结构用于转子位置检测。另外，文献[8-9]将基于SOGI的频率自适应滤波器用于异步电机的转子磁链观测算法中。

上述文章均是基于s域提出了新算法或新结构，然而工程实现时基本采用全数字实现方式，通常在z域中进行，而从s域到z域的转换过程中，所研究系统会产生性能的退化[10-18]，特别是对于信号-采样频率比比较大的应用场合，性能退化的影响难以忽略，因此有必要分析数字化实现对系统性能的影响。文献[10]详细研究了SOGI的不同离散方法，提出了一种可以将SOGI应用于不同场合的通用数字结构。文献[11]讨论了谐振控制器和滤波器在定点算法实现时的一些重要问题。文献[12]针对基于双积分器的谐振控制器数字实现时的性能退化问题，对数字实现算法进行了改进。文献[13]提出了一种结构高鲁棒性的定点数字谐振控制器。文献[14]对比分析了不同离散方法对谐振控制器性能的影响，指出了离散会带来频率偏移的问题。文献[15]采用不同方法对基于SOGI的自适应滤波器进行离散化，对比分析了性能差异，由于是针对电网的应用场合，该文章只对低频50Hz进行了对比分析。

虽然上述文章针对不同离散方法对数字系统性能影响进行了详细研究，但数字系统中的计算延迟使得反馈回路中必然存在滞后一拍问题，在s域内可由e-sT代替，目前绝大多数文献为了简便均选择忽略此问题，而此问题往往是造成数字系统性能退化的主要原因[16-18]。文献[16]提出一种基于FPGA/ASIC的全数字硬件化锁相环的建模方法，考虑了数字锁相环中存在的滞后一拍现象。文献[17]研究分析了全数字硬件化锁相环的性能退化规律，并指出了反馈中存在的滞后一拍现象是引起性能退化的主要原因。文献[18]在文献[17]的基础上提出了一种改进算法，消除了数字实现时的滞后一拍问题，显著提高了系统性能。

文献[16-18]主要对全数字锁相环中的滞后一拍进行分析并提出补偿措施，而基于SOGI的自适应滤波器为双闭环结构，此结构中的滞后一拍对系统的影响分析仍未见报道，因此非常有必要分析滞后一拍对全数字自适应滤波器的影响。

本文采用双线性变换对基于SOGI的自适应滤波器进行离散并分析其数字系统的性能退化规律。首先对考虑了滞后一拍的数字自适应滤波器的稳定性进行了分析，随后详细定量地分析了数字系统的性能退化规律，最后对理论分析进行了仿真证明和实验验证。

在应用于电网参数测量时，因为电压、电流的频率较低，此时的信号-采样频率比比较小，滞后一拍所造成的影响可以忽略不计，因此，绝大多数文献为了分析简便，通常在s域内忽略滞后一拍e-sT的影响，得到基于SOGI的自适应滤波器s域模型如图1(a)所示，实质为一个带通滤波器。设定频率参数ω*由外围自适应算法确定，决定了滤波器的中心频率；放大倍数k决定了滤波器的带宽，k值越小，带宽越小，灵敏度越高，需要根据实际情况折中选取。

采用双线性变换将图1(a)所示s域模型进行离散化，得到不考虑滞后一拍的传统z域模型，如图1(b)所示。图1所给出的s域和z域模型都未考虑滞后的影响，因此本文定义其为理想模型。

图1 自适应滤波器理想模型Fig.1 Ideal model of adaptive filter

采用全数字方式实现图1(b)的z域模型时，nT时刻的输入v(n)只能与上一时刻(n-1)T的反馈值v′(n-1)相减，得到nT时刻的误差值εv(k),此误差乘以系数k后送入SOGI进行运算，在SOGI中，kεv(n)同样只能与上一时刻(n-1)T的反馈值相减，然后经过一个积分器后得到nT时刻的更新值v′(n)，此值作为下一次计算的反馈值。这就造成z域实际模型如图2所示，即反馈存在滞后一拍现象。当滤波器在应用于电机位置、速度检测与估计等场合时，信号-采样频率比比较大，此时滞后一拍造成系统的静态和动态性能退化，其影响不能忽略。本文定义考虑滞后一拍的系统为实际模型。

图2 考虑滞后一拍的z域自适应滤波器实际模型Fig.2 Practical model of z-domain adaptive filter with one-step delay

数字自适应滤波器的性能退化主要表现为稳定性下降、频率偏移、幅值增益变化和非正交性。频率偏移指系统的实际选通信号频率偏离设定频率参数ω*，幅值增益指系统输出信号与输入信号的幅值之比。造成系统性能退化的主要原因便是系统数字化实现时存在的滞后一拍现象。

2.1 稳定性问题

图1(a)所示理想模型的s域传递函数为

(1)

式中：ω*为设定频率参数；k为放大倍数。

图1(b)所示理想模型的z域传递函数为

(2)

式中:a0=T2ω*2+2kTω*+4；a1=2T2ω*2-8；a2=T2ω*2-2kTω*+4；b0=b1=2kTω*；T为离散周期。

根据z域稳定性判据，式(2)稳定条件为：

(3)

易知，当不考虑滞后一拍时，放大倍数k与设定频率参数ω*均不受限制，系统恒稳定。

考虑滞后一拍的实际模型如图2所示，z域闭环传递函数为

(4)

式中:a3=T2ω*2+2kTω*-8；a4=2T2ω*2+4；a5=T2ω*2-2kTω*；b2=b3=2kTω*。

根据z域稳定性判据，式(4)的稳定条件为

(5)

取离散周期T=10-4s，式(5)所示实际模型的稳定区间如图3所示。

图3 数字自适应滤波器的稳定区间Fig.3 Stability area of digital adaptive filter

图3中，阴影区域为稳定区域，从图中可知，由于滞后一拍的引入，放大倍数k和设定频率参数ω*的取值范围均受到限制，系统的稳定性下降。

2.2 频率偏移

该小节对数字自适应滤波器的频率偏移规律进行理论分析。基于畸变预修正双线性变换的等效公式为

(6)

将式(6)代入式(4)，可得其在s域的传递函数

(7)

式中：c0=4α3；c1=2(2-kTω*)ωα2；c2=(2k-Tω*)Tω*ω2α；c3=T2ω*2ω2；d0=2kTω*ωα2；d1=2kTω*ω2α。

知s=jω，当考虑了滞后一拍，系统对应于ω*的实际选通信号频率为ω0。当ω=ω0时，为H1(s)相频特性曲线过0点，可得等式：

∠[d0(jω0)2+d1jω0]=∠[c0(jω0)3+

c1(jω0)2+c2jω0+c3]。

(8)

由式(8)整理可得ω0与ω*的关系等式为

(9)

式中α=tan(Tω0/2)。

可得实际数字系统的频率偏移量e为

e=ω0-ω*。

(10)

图4给出了离散周期T=10-4s，放大倍数k=0.6、0.8、1.0、1.2时的频率偏移量曲线。从图中可知：频率偏移量e随着ω*和k的增加呈现上升的趋势；k一定时，ω*取值范围受到临界稳定曲线的限制，当超过临界稳定曲线时，系统发散。取k=1，ω*=3 000 rad/s时，e的值为425 rad/s，相当于ω*的14.2%，已严重影响系统的选频性能。

图4 频率偏移量e的理论数据Fig.4 Theoretical results of frequency offset e

2.3 幅值增益

该小节在2.2小节的基础上，分析系统的幅值增益现象。知s=jω，系统对应于ω*的实际选通信号频率为ω0。当ω=ω0时，为H1(s)相频特性曲线过0点，将s=jω代入式(7)变换得

(11)

式中：a0=-2kTω*α2；a1=2kTω*α；b0=-2(2-kTω*)α2+T2ω*2；b1=Tω*(2k-Tω*)α-4α3；α=tan(Tω0/2)。

式(11)所对应的幅值增益为

(12)

图5给出了离散周期T=10-4s，放大倍数k=0.6、0.8、1.0、1.2时的幅值增益曲线。幅值增益随着ω*的增加呈现指数型上升的趋势；ω*取值范围受到临界稳定曲线的限制，当超过临界稳定曲线时，系统发散。取k=1，ω*=3 000 rad/s时，幅值增益为3.733 dB，即输出信号是输入信号的1.537倍。

图5 幅值增益的理论数据Fig.5 Theoretical results of amplitude gain

2.4 正交特性分析

由图1(a)可知，输出信号v′经过一个积分器再乘以ω*便得到输出信号qv′，因此两个输出信号之间的传递函数为

(13)

理想情况下，当信号频率ω=ω*时，Gqd(s)=-j，两个输出信号之间正交[15]。

实际数字系统中两输出信号之间的z域传递函数为

(14)

将式(6)代入式(14)得s域等效传递函数

(15)

式中α=tan(Tω/2)。

本节通过仿真验证上一节理论分析的正确性。

仿真参数设定如下：离散周期T=10-4s；放大倍数k选取为0.6、0.8、1、1.2；设定频率参数ω*的取值范围为整个稳定区间，间隔500 rad/s。

仿真过程中考虑滞后一拍，对采用双线性变换离散方法的全数字自适应滤波器模型进行仿真，根据系统的伯德图数据可以得到实际数字系统中对应着不同ω*的频率偏移量e以及相频特性曲线过0点处对应的幅值增益。

图6给出了系统的频率偏移量e的仿真数据。从图中可以看出，在稳定区间内，频率偏移量e随着设定频率参数ω*和放大倍数k的增加呈现上升的趋势。例如，当放大倍数k=1，设定频率参数ω*=3 000 rad/s时，e的仿真值为425 rad/s，相当于ω*的14.167%，此时e的理论计算值为424.7 rad/s，相当于ω*的14.157%，仿真值与理论值相差0.01%；k=1，ω*=6 000 rad/s时，e的仿真值为1 215 rad/s，相当于ω*的20.25%，此时e的理论计算值为1 215.1 rad/s，相当于ω*的20.251%，仿真值与理论值相差0.001%。可见，e的仿真数据与理论计算值基本一致。验证了数字系统频率偏移规律理论分析的正确性。

图6 频率偏移量e的仿真数据Fig.6 Simulation results of frequency offset e

图7给出了系统相频特性曲线过零点对应的幅值增益的仿真数据。从图中可以看出，在稳定区间内，幅值增益随着设定频率参数ω*的增加呈现指数型上升的趋势。例如，当放大倍数k=1，设定频率参数ω*=3 000 rad/s时，幅值增益仿真值为3.733 dB，即输出信号幅值是输入信号幅值的1.537倍，此时幅值增益的理论计算值同样为3.733 dB，与理论分析一致；当k=1，ω*=6 000 rad/s时，幅值增益仿真值为12.935 dB，即输出信号幅值是输入信号幅值的4.433倍，此时幅值增益的理论计算值同样为12.935 dB，与理论分析一致。验证了数字系统幅值增益规律理论分析的正确性。

图7 幅值增益的仿真数据Fig.7 Simulation results of amplitude gain

图8给出了不同设定参数的数字系统中，两个输出信号之间的相频特性曲线仿真图，从图中可知，两个输出信号之间相位恒差90°，与理论分析一致。验证了两个输出信号之间正交特性理论分析的正确性。

图8 Gqd(z)的相频特性曲线仿真图Fig.8 Simulation results of phase frequency curve of Gqd(z)

实验平台如图9所示，采用TI公司的28335DSP芯片实现本文数字自适应滤波器的功能，定时器设定100 μs作为中断周期，确保采样周期为10-4s，自适应滤波器的参数设定与仿真一致。采用Newtons4th公司的PSM1700频率响应分析仪(扫频仪)产生幅值为0.2 V的等差频率正弦信号，通过AD采样将正弦信号作为数字自适应滤波器系统的输入信号，扫频仪对数字系统的输入、输出信号进行采样分析获得数字系统的幅相频特性曲线的数据，最后对扫频仪得到的数据进行整理分析。实验工作流程图如图10所示。

图9 实验平台Fig.9 Experimental platform

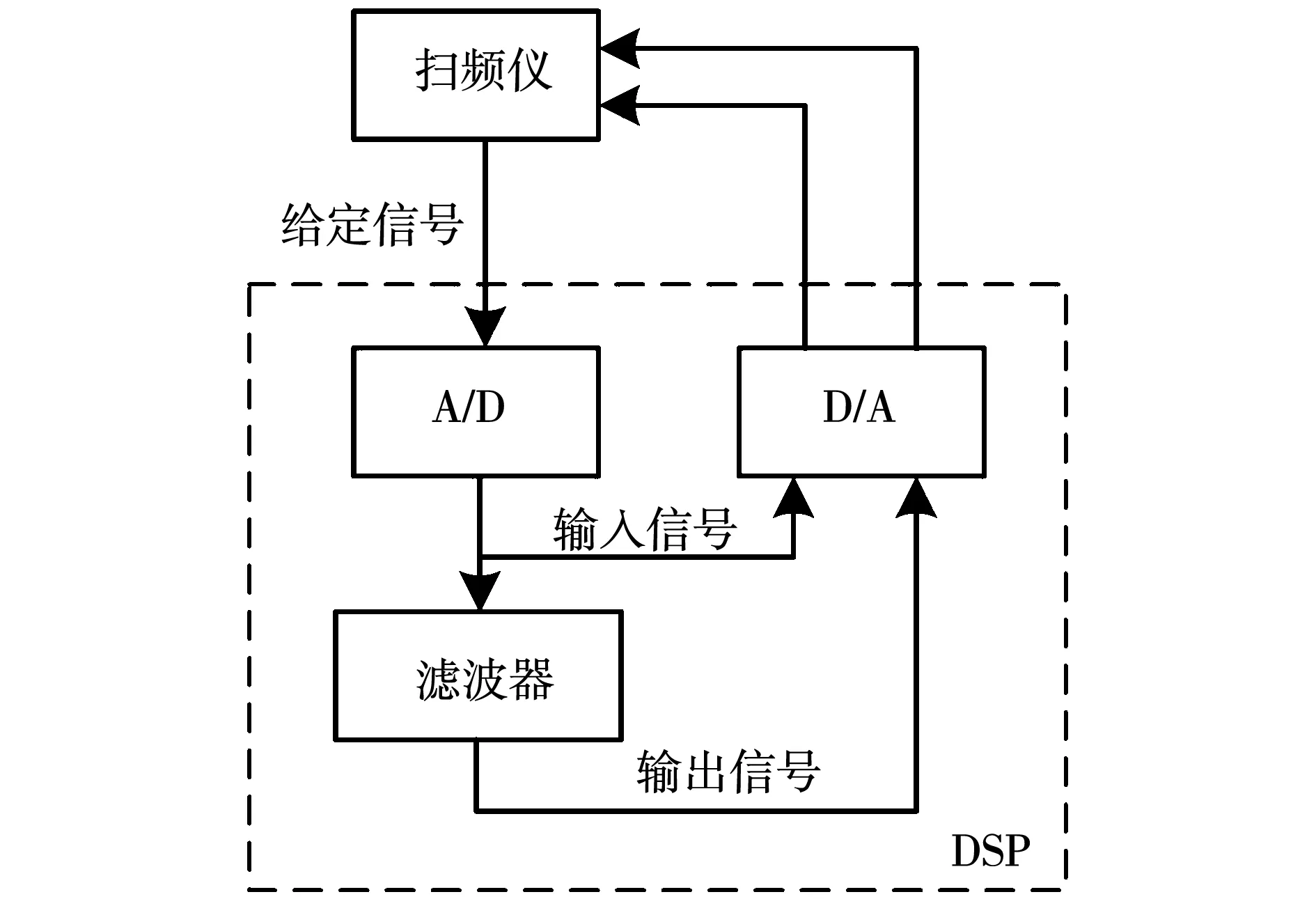
图10 实验工作流程图Fig.10 Experimental work flow chart

图11给出了数字系统的频率偏移量e的实验数据，从图可知，在稳定区间内，e随着设定频率参数ω*和放大倍数k的增加呈现上升的趋势；放大倍数k=1，设定频率参数ω*=3 000 rad/s时，e的实验值为416.733 rad/s，相当于ω*的13.9%，此时的e的理论计算值为424.7 rad/s，相当于ω*的14.157%,实验值与理论值相差0.257%；k=1，ω*=6 000 rad/s时，e的实验值为1 186.33 rad/s，相当于ω*的19.772%，此时e的理论计算值为12 515.1 rad/s,相当于ω*的20.251%, 实验值与理论值相差0.479%。可见，e的实验数据与理论计算值基本一致。随着ω*的增加，系统接近临界稳定，实验中测量频率偏移量e的误差有所增大，但仍小于1%。可验证频率偏移规律理论分析的正确性。

图11 频率偏移量e的实验数据Fig.11 Experimental results of frequency offset e

图12给出了系统的相频特性曲线过零点对应的幅值增益的实验数据，从图可知，在稳定区间内，幅值增益随着设定频率参数ω*的增加呈现指数型上升的趋势。放大倍数k=1，设定频率参数ω*=3 000 rad/s时，幅值增益实验值为3.828 dB，即输出信号幅值是输入信号幅值的1.554倍，此时幅值增益的理论计算值为3.733 dB，输出信号幅值是输入信号幅值的1.537倍，实验值与理论值相差0.095 dB；当k=1，ω*=6 000 rad/s时，幅值增益实验值为12.99 dB，即输出信号幅值是输入信号幅值的4.462倍,此时幅值增益的理论计算值为12.935 dB，输出信号幅值是输入信号幅值的4.434倍，实验值与理论值相差0.055 dB。与理论分析基本一致。可验证数字系统幅值增益规律理论分析的正确性。

图12 幅值增益的实验数据Fig.12 Experimental results of amplitude gain

采用双线性变换方法离散的数字自适应滤波器的设定频率ω*设为6 000 rad/s，放大倍数k=1。根据本文理论分析可得：实际选通信号频率ω0=7 215 rad/s，此时数字系统对应的幅值增益为12.93 dB，两个输出信号之间正交。

扫频仪对上述数字自适应滤波器扫频得到系统的幅相频特性曲线如图13所示。为了便于对比分析，图13中加入了理想自适应滤波器的幅相频特性曲线。理想滤波器的相频特性曲线过0点处对应的实际选通信号频率为6 000 rad/s，对应的幅值增益为0 dB；实际数字系统相频特性曲线过0点处对应的实际选通信号频率ω0约为7 188 rad/s，对应的幅值增益约为13 dB。

图13 滤波器频率响应实验结果Fig.13 Experimental results of frequency response of filter

向上述数字滤波器分别输入频率为6 000 rad/s以及7 215 rad/s的正弦信号，示波器采样所得到的时域图形如图14所示。当输入信号频率为6 000 rad/s时，输出信号较输入信号相位超前49.59°，幅值增益为7.3 dB；当输入信号频率为7 215 rad/s时，输出信号较输入信号相位滞后0.15°，幅值增益为12.9 dB。数字滤波器对频率为7 215 rad/s的正弦信号有更好的选通效果。

图14 滤波器时域输入输出波形Fig.14 Filter input/output waveform in time domain

扫频仪对上述数字自适应滤波器的两个输出端口进行采样分析可获得Gqd(z)的相频特性曲线，如图15所示。由图15可知，两个输出端口之间相位相差90°。可验证两个输出信号之间正交特性理论分析的正确性。

图15 Gqd(z)的相频特性曲线实验图Fig.15 Experimental results of phase frequency curve of Gqd(z)

本文对采用双线性变换离散的全数字自适应滤波器的性能退化规律进行了定量地理论分析，分别给出了实际数字系统的频率偏移和幅值增益曲线图以及正交性的理论分析结果。通过仿真与实验验证了理论分析的正确性。主要结论如下：

1)滞后一拍会造成数字自适应滤波器系统的稳定性降低，系统的放大倍数k与设定频率参数ω*的选取范围均受到限制，可依据本文对数字系统稳定域的理论分析结果调节参数。

2)在数字自适应滤波器的稳定区间内，由于滞后一拍的存在，频率偏移量和幅值增益均随着设定频率参数ω*的增加呈现上升的趋势；数字系统的正交性没有受到双线性变换的影响。

3)T一定时，设定频率参数ω*的增大，相当于信号-采样频率比增大。在信号-采样频率比高的应用场合，数字自适应滤波器频率偏移明显，可以依据本文的分析结果，在自适应算法中对设定频率参数ω*进行修正，数字滤波器有更好的选频效果。