基于同态加密的图像特征提取

常 亮（北方工业大学 信息学院，北京 100144）

0 引言

随着数字时代的到来，图像的数量急剧増长，使对大规模图像数据进行存储成为一个迫切需要解决的问题。得益于计算机技术的迅猛发展，云存储技术的出现，用户可选择将大规模图像数据外包到云端进行存储。这样不仅能减轻用户的存储和管理负担，还可以为用户的数据访问提供便捷服务。然而，作为一个第三方存储服务提供商，云服务器不是完全可信的[1]。图像内容中的一些敏感信息可能会泄露给云服务器，造成用户的隐私泄露。为了保护图像数据隐私，防止图像被非法访问。用户必须在图像外包以前对图像进行加密，然后再将加密后图像上传到云端[3]。使用图像时，用户需要先从云端将图像下载到本地，然后解密后才能使用。当图像数据的规模很大时，这种“加密上传、下载解密”的使用方式将会变得非常低效，这也违背云计算所倡导的数据便捷使用的初衷。所以对加密域的图像进行检索就变得非常重要，而在此之中，对加密图像进行特征提取则是重中之重。如何对加密域的图像进行处理、提取特征，并且不会使第三方获得所提取到的关键点，使对加密域内的图像进行处理这项工作具有重要的意义[7-10]。

现有的大多数方案采用Paillier加密来实现，然而Paillier加密具有计算量大、效率低等问题。为了解决该问题，本文利用对称同态加密算法来对图像进行加密，并基于密文域来实现图像的特征提取。它不仅保证外包图像的隐私安全，也保证了图像特征提取时的隐私。

1 对称同态加密算法的构造

1.1 对称同态加密算法

现有在密文域上对图像特征进行提取的方案大多数采用Paillier加密来实现，然而Paillier加密具有计算量大、效率低等问题，而对称加密具有计算量小、加密速度快、效率高等特点。为此，本文将构造一种新的对称同态加密算法用来对图像进行处理。其算法流程如下：

1）密钥生成

KeyGen(x)→(key,p)该密钥生成算法是一个概率算法。其中，p，q是大的素数且p＞＞q，b是一个随机整数。

2）加密

E(m,w,a)=(awq+bm)modp加密算法也是一个概率算法，用来对消息m进行加密。其中，a是一个小正整数，w是一个大的随机整数，m为输入的明文。

3）解密

D(key,c)=(cmodp)×q-1×b-1解密算法是一个确定性算法，c为所需的密文。

1.2 同态性证明

设c1，c2分别是明文i1和i2的密文，w1和w2是两个正的随机整数，a1和a2是两个正的小随机整数，p和q是两个大的素数并且p＞＞q，c1=(a1w1q+bi1)modp，c2=(a2w2q+bi2)modp。

同态加性证明：

上述的同态加法、同态减法这些操作表明：此加密算法可以对存储在云上的密文数据进行操作。

1.3 密钥空间分析

在本文中，密钥长度为150位，密钥空间约为2150位，密钥大小为2150的加密图像不易受到暴力破解的影响。因此，这个密钥大小就足够了。在实现过程中，密钥的位数可以增加。然而，这样做可能会导致系统的速度降低，对硬件的要求也会变高。

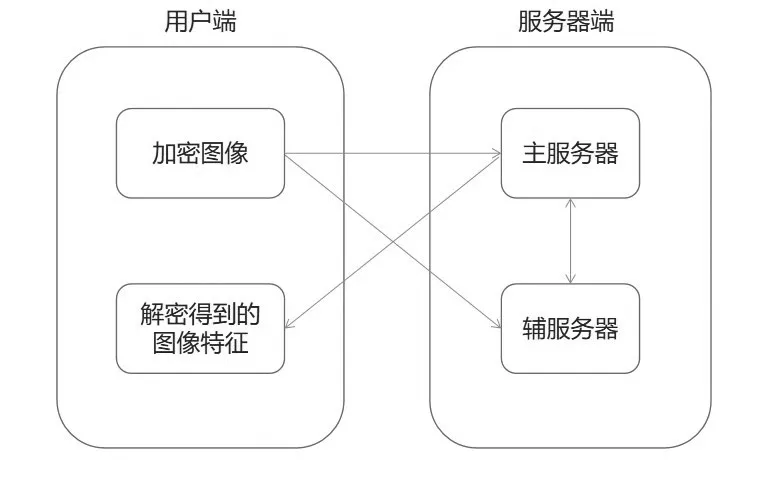
图1 用户与云端交互模型Fig.1 User cloud interaction model

2 同态加密的图像特征提取

2.1 用户与云端交互模型

如图1所示，在此模型中，服务器端由两个服务器组成，一个为主服务器S1，一个为辅服务器S2。首先，在用户端，用户加密图像image→Ie，生成密钥对(key,p)，并将密钥q分解为q1和q2，即q=q1*q2，并将它们分别发送给服务器端S1和S2。之后，由S1和S2联合计算得到图像的特征。最后，由服务器端将得到的结果发送给用户端，用户用密钥解密即可得到结果。

2.2 矩阵运算协议

1）加密矩阵的卷积运算(CMC)：给定一个公共矩阵B和加密矩阵A，则

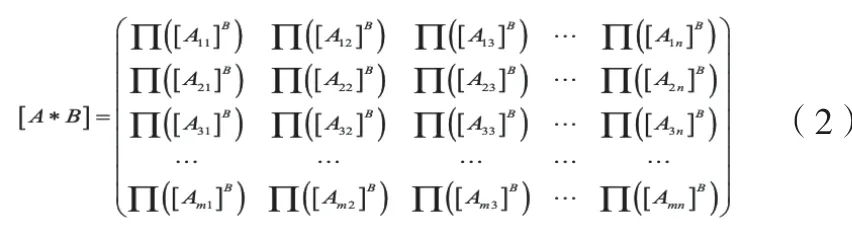
2）加密矩阵的乘法运算(CMM)：给定加密矩阵A和B，则

a） S1计算RA，RB(RAi,j,RBi,j，)，然后计算X=[A]·[RA]，Y=[B]·[RB]，X1=PDec(1)(X,b,q1)，Y1=PDec(2)(Y,b,q2)，然后将(X,Y,X1,Y1)发送给S2。

b） S2计算h=PDec(2)(X,X1,b,q2)·PDec(2)(Y,Y1,b,q2)，再将h加密为[H]给S1。

c） S1计算[A·B]=H·[RA·RB]P-1·[A]EP-PA·[B]EP-PB，其中EP为全P矩阵。

3）加密矩阵异或运算(CMXOR)：给定[A]和[B]，计算[A⊕B]=CMM([E]·[A]P-1;[E]·[B]P-1)·CMM([A];[B])，其中E为全1矩阵。

4）加密矩阵的差值运算(CMD)：给定两个加密矩阵[A]和[B]返回一个密文矩阵[F]用来表示这两个矩阵之间的差值。

a）S1计算[A']=[2A+E]=[A]2·[E]，[B']=[2B]=[B]2，其中E为全1矩阵。之后，S1选择两个随机矩阵[R]，[S]，其中||R||≤||P||/4，Si,j∈{0,1}，然后计算[T]=[R·(A'-B')·S+R·(B'-A')·(E-S)]，之后将[T]和PDq(1)([T])发送到S2。

b）S2将[T]解密后得到T，如果||Ti,j||≤||P||/2，那么S2令Uij=1，否则为0。

然后S2用密钥加密U，并把[U]发送给S1。

c）S1计算[F]=([U·S+(E-U)·(E-S)])=([U]S)·([E]·[U]P-1)E-S，若Fi,j=1，则ai,j＞bi,j，否则相反。

2.3 在加密域中对图像的特征提取

1）首先，在用户端生成密钥对(key,p)，并将图像进行加密image→Ie，将密钥q分为q1和q2且q=q1*q2，并将它们分别发送给服务器端S1和S2。S1收到I后，计算[D]，[D]=[(G(x,y,kσ)-G(x,y,σ))*I(x,y)] ，并生成27个相邻矩阵。

2）S1和S2共同计算[Ui]=CMD([D];[Ai])，1≤i≤27；若Uij=1，则为潜在特征点。

4）S1加密Hessian矩阵[H]，设

并计算

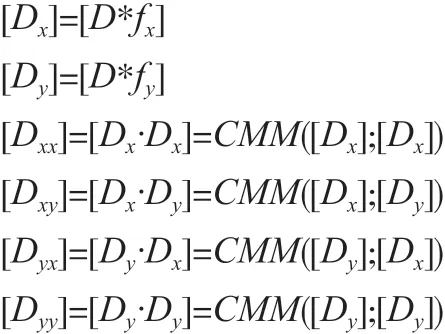
之后由S1计算

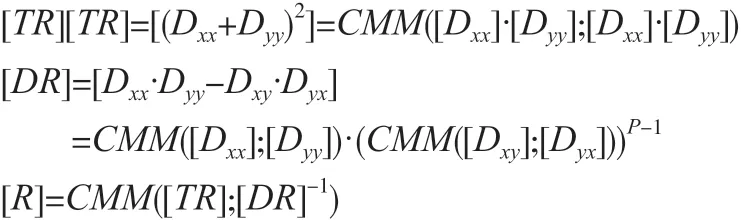
最后，S1用密钥加密阈值矩阵[ET]，ET是全阈值矩阵，S1和S2共同计算

S1将[F]发送给用户，用户用密钥即可解密获得特征值。

2.4 描述子的获取

1）给定[I]，S1计算[L]，并生成4个方向的矩阵L1，L2，L3，L4。

2）S1和S2共同计算

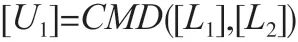
图2 实验结果Fig.2 Experimental results

表1 特征点匹配对比结果Table 1 Comparison results of feature point matching

3）S1和S2共同计算

对于一个4*4的子块，最终会形成一个64维的加密矩阵[V]，用户通过之前得到解密结果来解密[V]，便可得到描述子。[V]为被加密的特征描述子。

3 实验结果

本文在Intel(R)Core(TM)i7-8700CPU@3.20GHz环境下，使用Neo4j数据库进行实验，并选取了几幅有代表图像作为本次实验的结果，图2为本次实验结果的示意图，表1为选取了3组图像的3张图像作为本方案和原始sift方案提取出特征点的对比结果。

如图2所示，该方法实现了安全的外包，完成了对图像的特征提取，同时保持了关键点位置的隐私性。表1选取多幅图像的实验结果进行对比，表1表明：与明文域所提取出的特征相比，提取结果正确率接近90%，表明该方案具有较高的可行性。

4 总结

本文提出了在加密域内对图像特征提取的框架。适用于对隐私保护有需求的用户，当用户将加密数据作为查询内容发送至服务器端，服务器则可以在接收到加密的数据时进行运算，最终将对应的加密数据返回给用户。整个过程中，服务器端以及在传输过程中都是加密的图像，保护了数据隐私。