基于计算机视觉技术的焊接机器人定位精度分析

樊景博，田祎，任鑫博

(商洛学院 继续教育学院, 陕西 商洛 726000)

0 引言

计算机视觉技术中应用最为广泛的是双目视觉技术，该技术利用视差原理通过多个摄像机获得物体的信息[1]。在焊接技术领域，基于双目视觉技术在焊接机器人的末端安装摄像机，通过图像处理可以获得焊缝的坐标信息，并用以机器人末端的焊接过程。图像识别以及焊接机器人的精度均会对焊缝信息的计算产生影响[2]。本实验在商洛学院的陕西省尾矿资源综合利用重点实验室完成，采用加拿大Lumenera高性能工业相机进行拍摄，并利用“昆山一号”焊接机器人控制软件(昆山工业技术研究院机器人研究所与东南大学合作研发)进行数据分析和处理，用MatLab软件进行定位误差曲线绘制。本实验采用视觉方法对焊接机器人的定位精度进行了分析，通过建立视觉计算误差分析模型，确定了焊接机器人定位精度的影响因素，并确定了合理的系统配置参数。

1 焊接机器人的定位精度

焊接机器人的末端与安装在上面的摄像机组成了“手眼”系统[3]。机器人通过“手眼”系统将获取到的焊缝三维信息转换到机器人坐标系下。机器人的位姿关系对“手眼”系统标定精度产生了影响，并最终影响了焊接机器人的定位精度。

本文采用重复定位精度为±0.02 mm的MotoMan UP6型机器人和重复定位精度为±0.08 mm的新松SR6型机器人进行对比试验。焊接前需标定工具中心点(TCP)，使机器人绕轴旋转时，控制点的位置保持不变。然而控制点受标定误差和机器人精度的影响会产生一定误差。TCP标定后，UP6的精度可达0.3 mm，SR6的误差范围为3-5 mm。

焊接机器人定位精度的误差主要来源于机器人的重复定位和运动对视觉计算及定位精度的影响[4]。首先给出第一个实验，检测重复定位对视觉计算的影响。首先调整焊接机器人保持某一位姿，采用加拿大Lumenera高性能工业相机拍摄并计算标准棋盘格任意3个格子的距离；然后调整机器人改变位姿并再次保持原位姿，拍摄并计算任意3个格子的距离。实验用标准棋盘格，每个格子的尺寸为27×27 mm。每个位姿重复实验20次，将实验数据的平均值作为该位姿的实验数据，并与标准数据进行对比，如图1所示。

图1 实验用标准棋盘格

某4个位姿的实验数据分别为：80.772 0 mm、80.921 2 mm、80.449 6 mm和81.245 5 mm。3个格子的标准距离为81 mm，与实验数据的最大误差为0.550 4 mm。该误差来源于棋盘格印刷误差和机器人视觉计算误差等多个因素。为了研究机器人视觉计算受重复定位精度的影响，应将多个计算值的变化作为判定指标，因此采用数据离散度评价指标SD(标准差)判断重复定位精度对机器人视觉计算的影响大小。经计算，某一位姿20次重复实验的SD为±0.304 3 mm。

第二个实验检测机器人运动对视觉计算的影响。首先检测TCP误差恒定时位姿变化对视觉计算的影响。将标准棋盘格固定在机器人工作台上，标定TCP(标定误差为0.3 mm)后，改变机器人位姿，采用Lumenera高性能工业相机拍摄18幅图像对，利用“昆山一号”焊接机器人控制软件转换到机器人坐标系下计算棋盘格左上角第1点的坐标值，如图2所示。

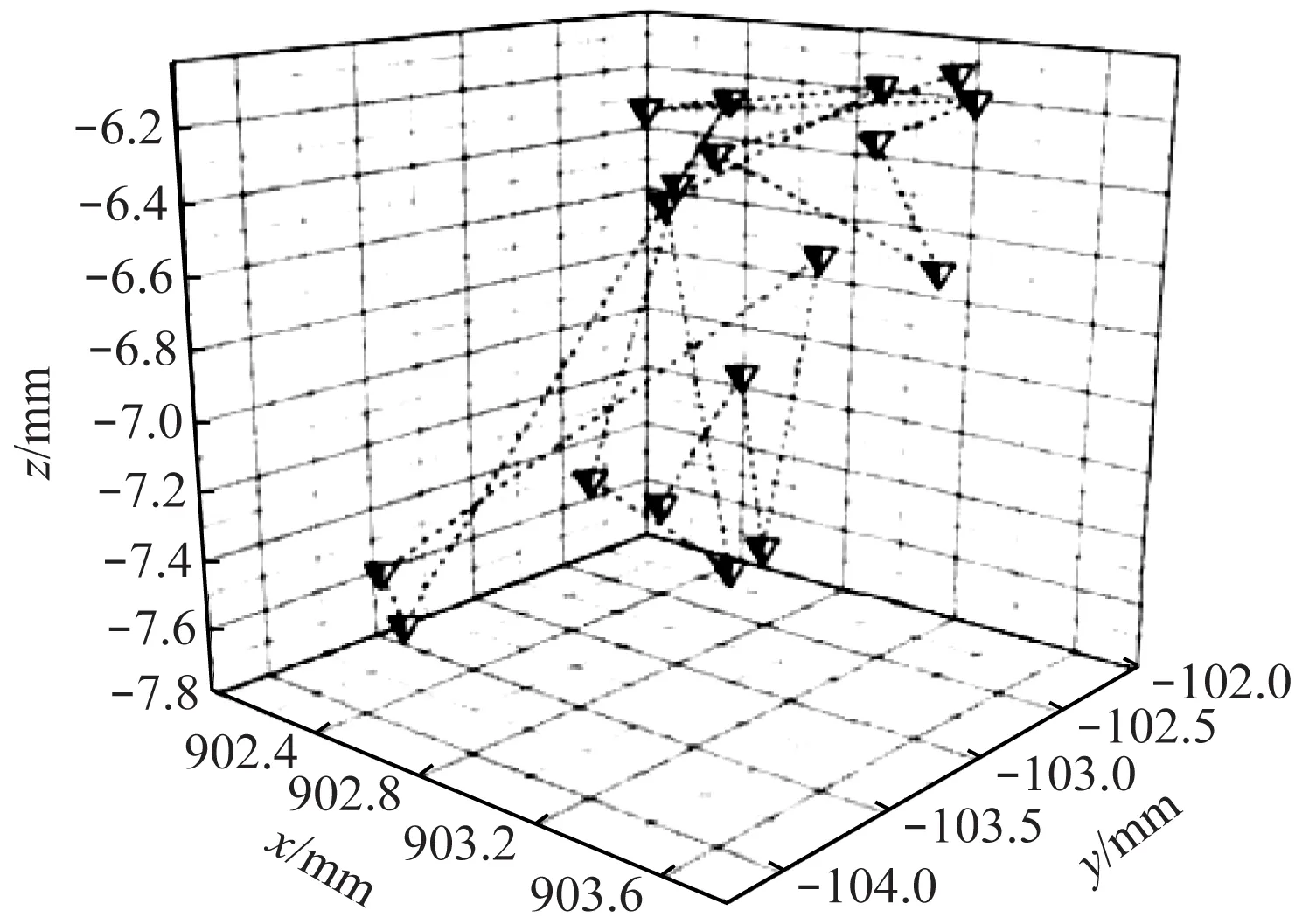
图2 TCP误差恒定时位姿变化对视觉计算的影响

经计算，实验数据的SD为±0.512 4 mm。采用类似的方法检测TCP标定对视觉计算的影响。首先通过标定手段改变TCP标定误差，并在每个标定误差下，改变机器人位姿，拍摄18幅图像对，并按照图2所示方法计算出X、Y、Z三个方向的SD和最大值，如表1所示。

表1 TCP标定对视觉计算的影响

分析表中数据可知，SD和最大误差均随着TCP误差的增大而增大。当TCP误差超过1.7后，计算误差达到了cm级，已无法满足实际应用。因为TCP误差并非精准控制的，1.7也非临界值。当前工业用焊接机器人的视觉计算精度主要受到TCP标定的影响，而成熟的工业机器人都具有较高的重复定位精度，对视觉计算的影响较小[6-7]，为了降低TCP误差，建议TCP标定误差控制在1 mm范围内，能够满足实验要求的同时，为该技术应用到成熟的焊接机器人提供了必要的参数价值。

2 视觉计算误差分析模型

有效视场范围内，待焊工件的放置位置影响着视觉计算的精度[8]。因此需对视觉系统配置即焊件摆放姿态以及传感器与焊件的相对位置对视觉计算的影响。

将两台Lumenera高性能工业相机任意放置进行拍摄，利用“昆山一号”软件采集图像信息后进行数据分析。建立的误差分析模型，如图3所示。

图中Ol、Or分别为两个工业相机的透视中心，并以Ol为坐标原点，两点连线为x轴，两点距离为b。CCD像面中，X轴与Y轴垂直，采用右手准则确定深度方向的z轴。双目传感器有效视场的高度与单台相同。本文仅对XOZ平面内的有效视场进行讨论，其宽度和深度由图3中的参数b、α和β决定。图中，θ为1/2视场角，β为1/2光轴夹角，将光轴交点向X轴投影，得到βl和βr，且有βl+βr=2β。当两个摄像机任意摆放时，图中XOZ平面内沿z轴方向MSN连线的以上区域为双目系统的有效视场，其宽度为ω。假设任意一点P(x,y,z)在两个摄像机图像上的投影分别为pl(ul,vl)和pr(ur,vr)。P点相对两摄像机透视中心即Ol、Or的张角分别为αl和αr。对模型进行简化，假设摄像机具有相同的配置，且对称放置，由几何关系即可计算出P点坐标x、y、z的值。

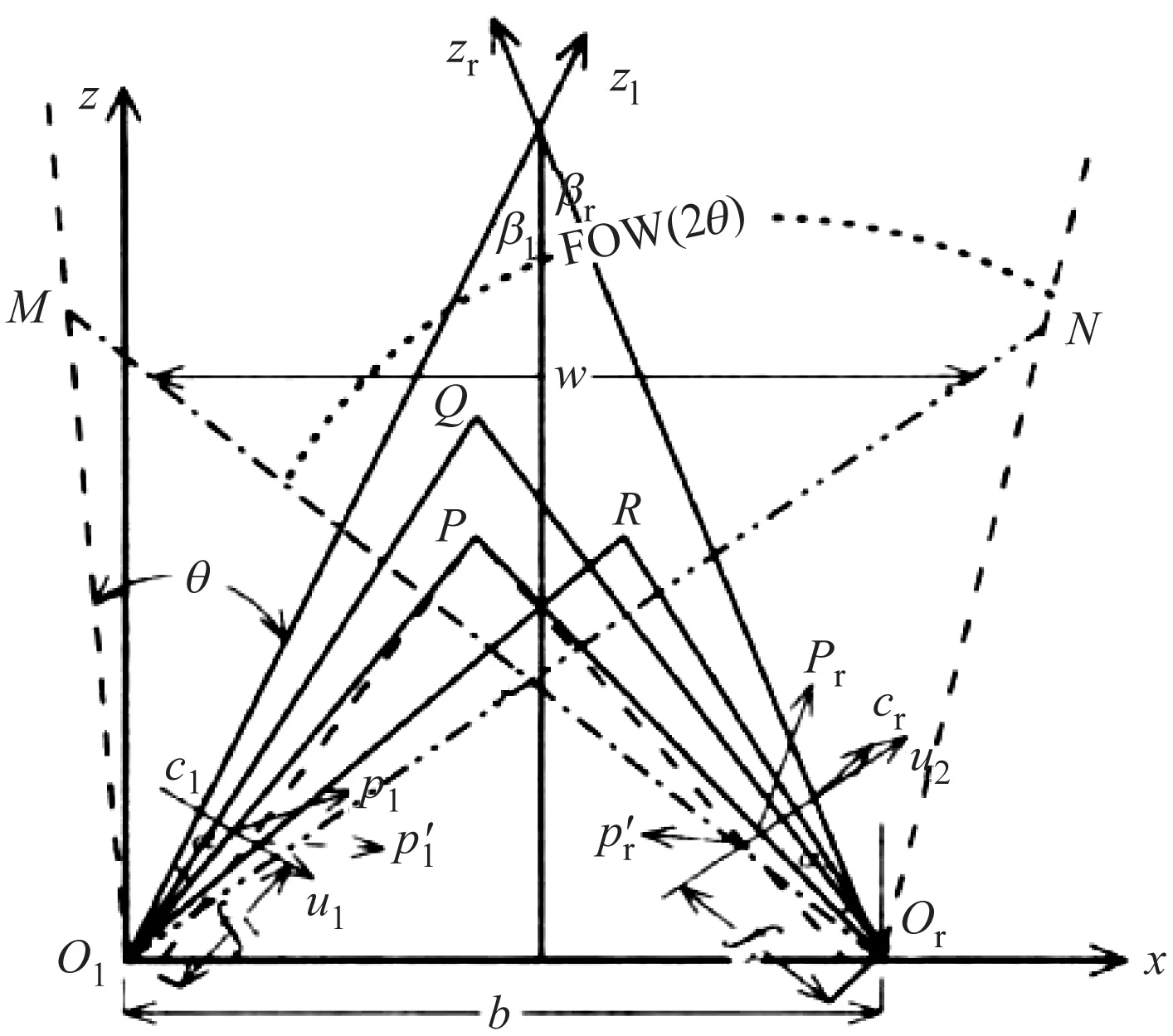
图3 两个摄像机任意放置时的误差分析模型

3 系统配置对定位精度的影响

像平面内的像素坐标和传感器的结构参数均会对空间点的三维坐标计算产生影响。由视觉计算误差分析模型可知，影响P点定位精度的因素有P点在图像上的投影误差和坐标提取误差；传感器的标定误差和结构参数b，f，βl和βr。

图像校正和图像匹配因提取图像产生的误差称为图像误差，设摄像机在u方向上的图像误差为Δε，在v方向上的图像误差为Δω，且图像误差伴随成像位置的改变不发生变化。将P点的坐标值x、y和z分别对u和v求导，即可求出图像误差对定位精度的影响。为了简化计算，假设视觉系统配制不变，u方向和v方向的图像误差相等，即有b和f为定值，βl=βr=β，Δε=Δω。根据误差分析理论[5]，采用x、y、z方向的误差表示定位综合误差Δ的表达，如式(1)。

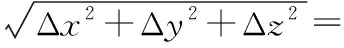
(1)

本文视觉系统标定后，fx和fy分别为587.962 4像素和585.875 1像素，b为228.964 7 mm。设图像误差Δε和Δω均为0.5像素，P点坐标x和y均为100 mm，可得到定位误差与测量距离z值的关系曲线，如图4所示。

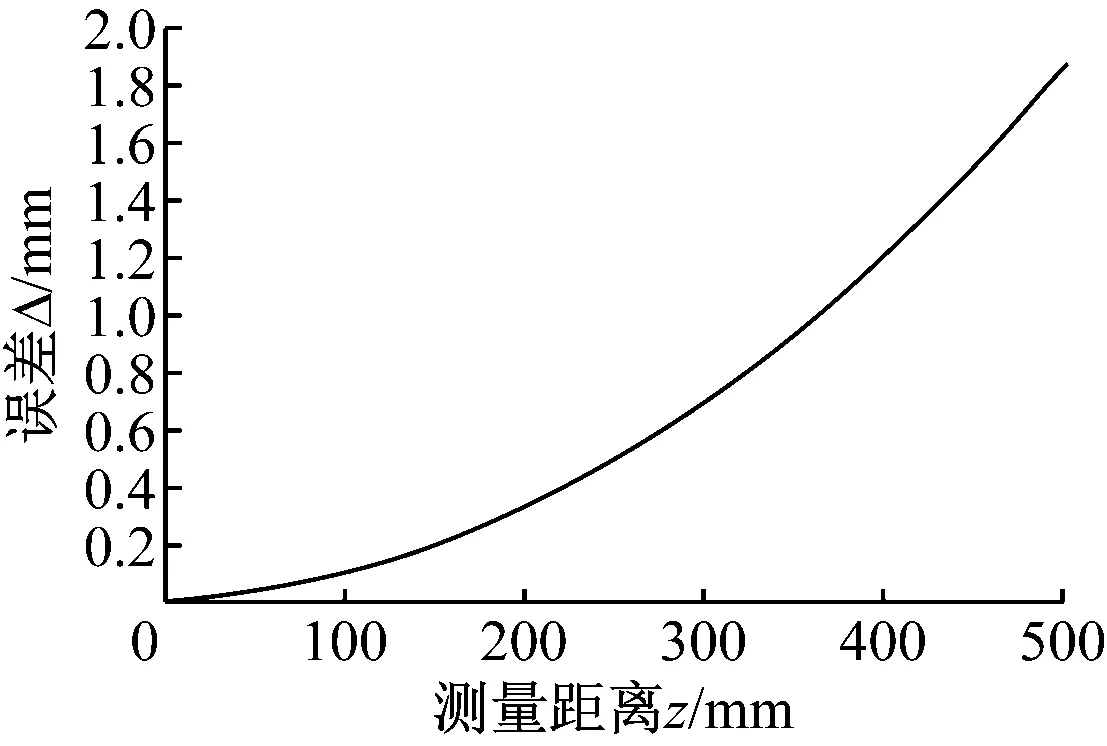
图4 定位误差与z值的关系曲线

可以看出，定位误差伴随测试点与CCD距离的增大而逐渐增大。考虑实际应用中工件摆放以及有效视场等因素，建议焊接机器人合理的工作范围为150-450 mm。

由图3视觉误差分析模型可知，R点与P点的高度相同，αl和αr随x值的不同发生了变化。由此可知，x值改变，计算误差也会随之改变，但无法判断其变化趋势。设z为200 mm，得到定位误差与x值的关系曲线，如图5所示。

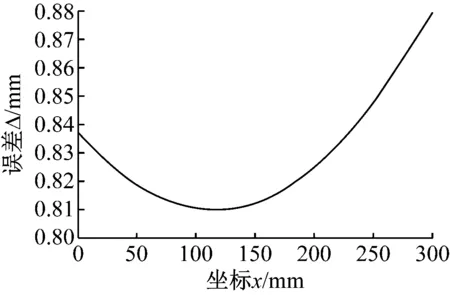
图5 定位误差与x值的关系曲线

可以看出，x=b/2时，定位误差最小；相比定位误差随z值的变化，其变化幅度较小，由此表明，测量距离的改变对定位误差的影响较大。

4 总结

焊接机器人定位精度的误差主要来源于机器人的重复定位和运动对视觉计算及定位精度的影响，其中，重复定位的影响较小，建议TCP标定误差控制在1mm范围内。通过建立视觉计算误差分析模型和定位综合误差表达式可知，定位误差伴随测试点与CCD距离以及测试点x值的改变而改变，其中测试距离的影响较大，建议焊接机器人合理的工作范围为150-450 mm。