圆锥曲线中与离心率相关的性质

云南省弥勒市第一中学(652399) 孔繁文

题目(2020年高考数学全国卷理科数学模拟试题(十一)第20 题)已知椭圆C:= 1(a ＞0,b ＞0)的右焦点为F,点M(1,)在椭圆C上且MF垂直于x轴.

(Ⅰ)求椭圆C的方程;

(Ⅱ)设P为椭圆C上的动点,直线PM与x=4 交于点N,求证: 点N到直线PF的距离为定值,并求出这个定值.

答案(Ⅰ)椭圆C的方程为=1;(Ⅱ)定值为3.

本题着重考查椭圆的方程,点和直线、点和椭圆的位置关系,直线和直线的方程,点到直线的距离等知识,同时还考查划归与转化的数学思想及综合运算的能力.笔者对(Ⅱ)进行深入探究,得到了圆锥曲线中与离心率相关的性质.

命题1F和l分别是椭圆Γ:=1(a ＞b ＞0)的焦点和相应准线,若一条直线与椭圆Γ 相交于A、B两点,与l相交于C点,且BF垂直于x轴,则点C到直线AF的距离是椭圆Γ 的通径与其离心率之比的一半.

证明依题意, 设F(c,0), 则直线l的方程为x=设A(x0,y0),,t); 将x=c代入= 1 解得y=, 于是因为A,B,C三点共线,所以因为直线AF的方程为y=即y0x −(x0−c)y −cy0=0,所以点C到直线AF的距离

其中e是椭圆Γ 的离心率,所以点C到直线AF的距离是椭圆Γ 的通径与其离心率之比的一半.

又由于直线AB的方程为c), 将点C的坐标,t) 代入AB的方程解得t=所以所以直线CF的斜率kCF=又因为直线AB的斜率kAB=所以kAB −kCF=即|kAB −kCF|=e(其中e是椭圆Γ 的离心率).于是又得

命题2F和l分别是椭圆Γ:=1(a ＞b ＞0)的焦点和相应准线,若一条直线与椭圆Γ 相交于A、B两点,与l相交于C点,且BF垂直于x轴,则直线AB的斜率与直线CF的斜率之差的绝对值是椭圆Γ 的离心率.

命题3F和l分别是双曲线Γ := 1(a ＞0,b ＞0)的焦点和相应准线,若一条直线与双曲线Γ 相交于A、B两点,与l相交于C点,且BF垂直于x轴,则点C到直线AF的距离是双曲线Γ 的通径与其离心率之比的一半.

证明与命题1 类似,从略.

命题4F和l分别是双曲线Γ := 1(a ＞0,b ＞0)的焦点和相应准线,若一条直线与双曲线Γ 相交于A、B两点,与l相交于C点,且BF垂直于x轴,则直线AB的斜率与直线CF的斜率之差的绝对值是双曲线Γ 的离心率.

证明与命题2 类似(略)

命题5F和l分别是抛物线Γ :y2= 2px(p ＞0)的焦点和准线,若一条直线与抛物线Γ 相交于A、B两点,与l相交于C点,且BF垂直于x轴,则点C到直线AF的距离是抛物线Γ 的通径与其离心率之比的一半.

证明依题意,设0),则直线l的方程为x=设A(x0,y0),C(,t);将x=代入y2= 2px解得y=±p,于是,±p);因为A,B,C三点共线,所以

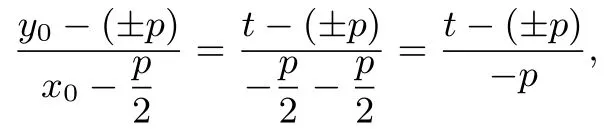
即−py0=因为直线AF的方程为y=即y0x −(x0−= 0,又=2px0,所以点C到直线AF的距离

其中1 是抛物线Γ 的离心率,所以点C到直线AF的距离是抛物线Γ 的通径与其离心率之比的一半.

又由于直线AB的方程为y −(±p) =将点C的坐标,t) 代入AB的方程解得t=所以所以直线CF的斜率

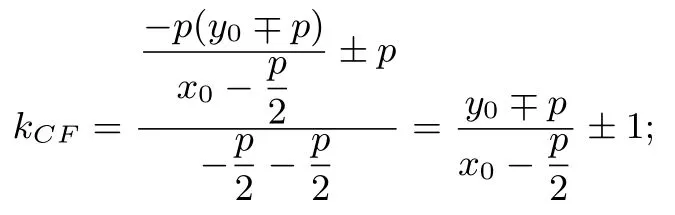
又因为直线AB的斜率

所以kAB −kCF==∓1, 即|kAB −kCF|= 1(其中1 是抛物线Γ 的离心率) .于是又得

命题6F和l分别是抛物线Γ :y2= 2px(p ＞0)的焦点和准线,若一条直线与抛物线Γ 相交于A、B两点,与l相交于C点,且BF垂直于x轴,则直线AB的斜率与直线CF的斜率之差的绝对值是抛物线Γ 的离心率.

由上述命题可得圆锥曲线中与离心率相关的如下两个性质:

性质1F和l分别是圆锥曲线Γ 的焦点和相应准线,若一条直线与Γ 相交于A、B两点,与l相交于C点,且BF垂直于F所在的轴,则点C到直线AF的距离是Γ 的通径与其离心率之比的一半.

性质2F和l分别是圆锥曲线Γ 的焦点和相应准线,若一条直线与Γ 相交于A、B两点,与l相交于C点,且BF垂直于F所在的轴,则直线AB的斜率与直线CF的斜率之差的绝对值是Γ 的离心率.