考虑动态分合的可重构设施布局方法研究

丁祥海，诸天亮，姚文鹏

(1.杭州电子科技大学 工业工程与管理研究所，浙江 杭州 310018;2.中国移动通信集团衢州分公司，浙江 衢州 324000)

可重构设施布局(Reconfigurable Facilities Layout，RFL)是一种下一生产周期生产信息(产品种类、工艺路线等)已知，考虑当前车间设施布局，以某一个(或多个)绩效为目标的布局方法[1]，在多品种变批量的市场中，获得了广泛应用[2-5]。但是RFL通常不考虑设施拆分布置的情况。当车间加工的物料有多种，工艺路线互不相同时，它会导致工艺路线存在迂回，造成浪费从而提高了成本。分布式布局(Distributed Facilities Layout，DFL)虽然考虑了同类设施分开布置，但是基于多个生产周期预测数据，没有考虑当前车间布局情况[6]。市场需求是动态变化的，预测与实际需求之间往往存在较大偏差，这既会影响DFL方法的效果，又会催生物料流动态分配难题[7]。本文为了解决RFL的浪费问题和DFL的单周期效果差问题，考虑同类设施分合情况，提出一种兼具RFL单周期优势和DFL分布优势的布局方法，将此方法命名为动态分合可重构设施布局(Dynamic Combination Reconfigurable Facilities Layout，DC-RFL)方法。目前，分别研究RFL和DEL的文献较多，但研究DC-RFL的文献较罕见。

一、动态分合可重构设施布局问题

(一)问题描述和假设

DC-RFL考虑了同类设施的分合情况，在兼具RFL和DFL各自优势的情况下，解决了可能出现的工艺路线迂回导致的浪费问题、多周期预测导致的单周期效果差问题。该方法扩大了问题的规模，而且会引起物料分配的动态性，是一个比RFL和DFL更难的问题。

1.布局方案的描述和假设

为了能够具体、可视化地描述设施的位置和面积信息，这里采用空间填充曲线(Space filling curve)的方法。它将车间视为一块网格图形，图形面积即车间面积，并将图形分为若干面积相等的网格，网格按照空间填充曲线的规则连续编号，将设施以网格为最小单位摆放。假设车间的入料口和出料口唯一，有M种设施需要进行布局；Mmi表示第m类第i台设施(m=0，1，……，M+1)。当m=0时表示入料口，m=M+1时表示出料口，入料口和出料口位置固定，i≥1。各种类单台设施所需面积和生产能力已知且不变，布局方案可用设施起始网格编码表示。

2.设施分合的描述和假设

在DC-RFL中，同一类设施的拆分有多种情况，如3台钻床可能的拆分方式：(钻1钻2钻3)、(钻1，钻2钻3)等。为了简化问题，引入设施相邻和生产区域的概念。若设施A的最大网格编码为k，设施B的最小网格编码为k+1，则设施A和B相邻。相邻的同类设施组成一个生产区域。进行如下规定：①同类型生产区域由相邻变为不相邻称为分离；由不相邻变为相邻称为合并。分离后的两个生产区域，单独布局，合并后的两个生产区域，作为整体参与布局；为进一步简化问题，假设同类设施的面积需求和生产能力相同。②某类设施的可拆分数等于该类设施的数量，M种设施的可拆分数可以用一个M维的向量来表达。基于以上假设，可以减少设施的拆分方式，如上述钻床的情况，可以只需考虑(钻1,钻2,钻3)一种拆分方式，其它方式可以在布局过程中，通过不同的合并方式获得。

3.物料分配的描述和假定

(二)模型构建

把物料加工过程简化为一个物流系统[8-9]，以物料小车运送物料的过程为对象，不考虑各生产区域的等待、加工和搬运等细节情况，从三个方面重点考虑生产区域的能力约束：一是总量约束，即各类设施总负荷不能超过该类设施总生产能力；二是拆分数约束，考虑到设施总生产能力和实际负荷大小，对布局方案的多样性做出限制；三是物料小车运输路径约束，小车运输路径是根据下一生产区域剩余生产能力来判断选择的。在此基础上，以物流成本和重构成本最低为优化目标,建立DC-RFL模型如下：

(1)

(2)

(3)

(4)

式(1)是总成本费用的目标函数，前项是物流成本，后项是重构成本；式(2)是对满载量的约束，表示任一生产区域，其生产能力至少满足小车一次满载量负荷；式(3)是对周期加工任务的约束；式(4)考虑可能存在SPAj生产能力未充分利用时加工物料总数和设施拆分数的共同约束，rem为取余函数。

下面给出一个小规模算例，说明上述模型参数定义和约束设置等的可行性和有效性。设车间内网格按照空间填充曲线规则的排列顺序及坐标，入料口是编码为1的网格，坐标为(0,0)，出料口是编码为64的网格，坐标为(5,8)。设车间内有3类生产设施M1至M3，所占车间网格数分别为30、12、20，初始网格数编号分别为1-30、31-42、43-62。下一个周期的物料加工种类为a1、a2，a1的工艺流程是in→M1→M3→M2→out，加工数量为500，a2的工艺流程是in→M2→M1→out，加工数量为500。in到M1、M2、M3、out的单位成本系数分别为0.15、0.17、0.14、0.12;M1到M2、M3、out的单位成本系数分别为0.13、0.13、0.15;M2到M1、M3、out的单位成本系数分别为0.16、0.17、0.13;M3到M1、M2、out的单位成本系数分别为0.12、0.14、0.15。设施重构成本C=[15,15,30]；设施拆分数矩阵m=[2,1,1]；各类设施的总生产能力Cb=[2 000,3 500,2 500]；物料小车的满载量Fl=50。经计算得12种布局，其中初始布局方案为M1→M2→M3，RFL方案为M2→M1→M3，DC-RFL方案为M11→M3→M2→M12，成本费用分别为2 490.77元、2 281.55元、2 029.26元，可以发现DC-RFL的总成本费用更优。

二、模型求解

(一)算法设计

染色体编码。染色体即为设施拆分编码，例染色体i的编码(1 0 1 0 1 )，表示5类设施M1至M5中M1、M3和M5拆分。染色体的基因数量即为设施的种类数。染色体基因全为“0”对应RFL情形；染色体基因全为“1”对应单周期的DFL。每个染色体对应一个布局方案及其目标函数值，这个布局方案和目标函数值是通过粒子群算法获得的。

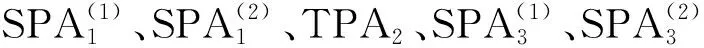
粒子更新。个体最佳位置由Lkhg确定，是第g次迭代的最佳布局；全局最佳位置由Lkh确定，它是染色体h决定的粒子群迭代过程中的最佳方案。粒子更新迭代公式如下[9]。

(5)

为了防止陷入局部收敛，引用遗传算法的变异概念，在每次粒子更新时随机产生因数Kr(0a，(a为一个设定数，0

粒子解码。通过式(5)获得的粒子位置值需要和空间填充网格编码对应，这个过程称为解码。对新产生的粒子中各个体位置值的大小进行排序，位置值最小个体对应的生产区域放置在空间填充曲线的入口端，然后根据顺序和各生产区域面积数确定各生产区域起始网格编号。例如，粒子A(x1,x2,x3,x4,x5,x6,x7,x8)对应的位置值为(0.55，0.32，0.94，0.41，0.55，0.73，0.29，0.77)，根据大小可得排序向量B=(4,2,8,3,5,6,1,7)。向量B中数值为1的元素对应向量A中的元素x7，表示x7排在空间填充曲线最前端，故元素x7的起始网格编码为“1”；向量B中数值为2的元素对应A中的元素x2，故元素x2应紧邻在x7后面，其起始网格编码为x2的起始网格编码值加上x2所需的网格数减去1；其余类推。

(二)遗传-粒子群混合算法流程设计

之所以采用遗传-粒子群混合算法而不单独只用其中一种算法来实现重构布局的计算主要有两个原因：其一是上文提到的为了实现在设施拆分信息编码不变时能够改变设施布局信息编码的目的；其二是若采用单一算法，则会对各类设施全部拆分后进行重构，而混合算法则会优先确定设施是否需要拆分。遗传-粒子群混合算法具体步骤如下：

1.设置好相关参数，输入车间初始布局和下一周期的产品需求等数据；

2.利用遗传算法进行运算，确定设施的拆分编码，即拆分方案；

4.判断是否满足粒子群算法终止条件，满足则转到下一步，否则重复步骤3；

5.保存该拆分编码对应的最优设施布局方案；

6.判断是否满足遗传算法终止条件，满足则算法结束，选取最满意的拆分编码及其对应的设施布局方案，否则重复步骤2，并且为了避免最优解的遗漏，同时保存每代种群中具有最优目标值的拆分编码及其对应的设施布局方案。

步骤1中输入数据包括基础数据、物流数据和程序运行数据三类。基础数据包括各类设施面积大小、初始布局方案、费用值(包括重构成本、运输成本)等；物流数据包括下一周期的物料种类、物料量、物料加工工艺流程等需求数据；程序运行数据包括种群规模、最大迭代次数、最大进化代数、Kr值等。

三、算例分析

(一)基本数据

算例采用MatlabR2018a编码实现。在单周期情况下，分别就DC-RFL、RFL和DFL进行对比分析，从而验证所提出方法的优越性。

图1 车间网格编码及坐标

A车间设施布局以网格编码及坐标的形式表示如图1，车间内仅有一个入料口和一个出料口，坐标分别为(0,0)和(16,30)。A车间有7种加工设施M1至M7，所占车间网格数分别为96、96、60、96、60、96、96，初始网格数编号从1-564按照M1至M7的顺序依次排列，例如M1为1-96、M2为97-192。M1-M7的可拆分数分别为2、4、3、5、2、3、2；重构成本分别为100、100、150、100、200、100、150；生产能力分别为2 000、3 500、2 500、2 000、3 000、2 500、2 500。物料小车满载量Fl=50。下一周期有5种加工物料b1至b5，加工数量分别为500、600、450、500、550，工艺路径为b1：in→M1→M2→M5→M6→M3→M2→M4→out；b2：in→M4→M5→M3→M7→M6→M2→M3→M7→out；b3：in→M2→M5→M6→M7→out；b4：in→M2→M7→M5→M1→out；b5：in→M3→M6→M5→M2→M1→out。物料成本系数cij如表1。

表1 物料运输成本系数cij

(二)计算结果及分析

1.计算结果

粒子群参数设置：种群规模为10，C1=C2=2，w=0.5，迭代次数1 000。遗传算法参数设置：种群规模为10，进化代数30，交叉概率为60%。应用遗传-粒子群混合算法运行20次后，DC-RFL的最优结果为21 195.03，对应拆分码为[1 1 0 1 1 1 1]，布局方案如表2，结果平均值为21 453.34。

表2 DC-RFL最优结果的布局方案信息

2.比较分析

与RFL比较。拆分码[0 0 0 0 0 0 0]对应RFL。此时用单一的粒子群方法求解。应用改进粒子更新过程的PSO运算20次，迭代1 000次，得到最优解为28 239.84元，平均值为28 426.44元，得到最优解的平均迭代次数为68次。应用未改进粒子更新过程的PSO运算20次，迭代1 000次，得到最优解为28 239.84元，解最大值为31 849.83元，平均值为29 944.33元。

与单周期DFL比较。拆分码[1 1 1 1 1 1 1]对应DFL(单周期)。这种情况运算20次得到最优解为22 554.4元，对应布局方案如表3。考虑到DFL的所有可能布局方案涵盖了DC-RFL的结果，其全部寻优结果中也存在应用DC-RFL后得到的较优目标值，再以更大迭代次数(考虑到运算时间，迭代上限为10 000次)对DFL进行多次寻优，较优解(目标值为21 815.2元)仅出现一次，平均值为22 429.34元。

表3 单周期下DFL最优结果的布局方案信息

结果表明：①在粒子更新时添加随机因数Kr能有效避免粒子群算法陷入局部收敛；②DC-RFL能够获得比RFL更优的布局方法；③DC-RFL比DFL(单周期)具有更快的搜索效率。

四、结论

针对传统可重构设施布局(RFL)的同类设施不拆分可能导致的工艺路线迂回浪费问题和分布式布局的多周期预测可能导致的单周期效果差问题，本文提出了新的布局方法，即动态分合可重构设施布局(DC-RFL)，它兼具可重构设施布局(RFL)的单周期最优化优势和分布式布局(DFL)的选择优势。DC-RFL最大的难题是如何分合设施，以及分合后物流在设施之间如何分配。引入空间填充曲线来表征车间中设施的摆放位置和形状，较方便地将设施的分合问题转化为网格号是否相连的问题；利用就近原则和设施的能力约束，有效解决了分合后设施之间的物流分配问题。

本文构建了动态分合可重构设施布局优化模型，并提出了一种适用的遗传-粒子群混合算法求解模型，该算法求解是一个两步骤决策问题，旨在以遗传算法模块搜寻到的设施拆分方案为基础，通过粒子群算法模块对各类拆分方案不断寻优得到最终结果。最后寻优得到的结果与原始布局方案和RFL进行对比，发现DC-RFL方法能以更短的搜索时间和更少的搜索次数得到一个总成本更低的布局方案，成本分别降低40.02%和24.94%。在如今多品种变批量的市场环境中，企业车间如何降低物流方面的成本投入是一个重要的管理问题。本文方法综合考虑了物流成本和重构成本，贴近现实情况，极大提高了企业车间的管理效率，大大降低了设施布局方面的投入。

本文不足之处在于，只考虑同类设施之间的分合问题，没有考虑不同类型设施可能因为物流的紧密性，可以组合成单元参与布局的情况。另外，本文在目标函数只涉及了成本费用，没有全方位考虑到在制品库存、生产工序的交叉等因素。课题组将继续从事这方面的研究。