关于二部图上的颜色最多独立集问题

周 圆，陈光亭，陈 永，张 安

(1.杭州电子科技大学理学院，浙江 杭州 310018；2.台州学院电子与信息工程学院，浙江 台州 318000)

0 引 言

顶点着色图在多个学科领域有着十分重要的作用，文献[1]介绍了其在生物信息学中的应用。文献[2]给出了在一般图中找最大独立集问题是NP-hard。文献[3]提出限制奇偶度时的有界度图上的近似算法，对于一些特殊的图，文献[4-6]分别提出在无爪图(claw-free graph)、无P5路的图(P5-free graph)和完美图(perfect graph)中，寻找最大独立及问题(Maximum Independent Problem，MIP)是多项式时间内可解的，文献[7]提出，对于余图(cograph)和弦图(chordal graph)，可在线性时间内解出MIP问题。当前对颜色数最多的独立集问题(Maximum Colorful Independent Set Problem，MCISP)的研究中，文献[8]提出聚类图(cluster grpah)和树(tree)中的MCISP问题是多项式时间内可解并给出相关算法，而在无P5路(P5-free graph)图和余图(cogrpah)中，求解MCISP问题是NP-hard。

1 一般二部图上的MCISP问题

定义1给定任意图G=(V,E)，将图G中的顶点集V分为两部分，分别是V1和V2且V1和V2都是独立集，图G中的边集E由V1中的顶点到V2中的顶点的连线组成的图称为二部图[10],记作G=(V1,V2,E)。

定义2给定任意二部图G=(V1,V2,E)，V1中的每一个顶点与V2中的每一个顶点之间都有边的图称为完全二部图[10]，记作KV1,V2。

定义3给定任意二部图G=(V1,V2,E)和颜色集C，使得G中每个顶点都着有C中至少一种颜色的图为顶点着色图[8]，其中C中的颜色由自然数N表示，不同的自然数i表示不同的颜色，i∈N。|C(Vi)|表示不同集合的不同颜色数，i∈{1,2}，记作Gc=(V1,V2,E)。

对于任意给定的顶点着色二部图Gc=(V1,V2,E)，在图G上找到一个包含G中顶点颜色数最多的独立集S，其中集合S记作算法解得到的不同颜色顶点组成的集合，S*表示最优解中颜色不同的顶点组成的集合，这一问题叫做二部图上的MCISP问题。

下面给出求解MCISP问题的一个多项式时间近似算法。

算法1:一般二部图上的近似算法输入:1个简单二部图Gc=(V1,V2,E)输出:Gc中包含颜色最多的独立集S步骤:令S=⌀,比较集合V1与V2中的颜色种类,若C(V1)≥C(V2),则令S=V1,否则令S=V2,结束算法。

定理1算法1的最差情况界为2且是紧的。

证明不妨假设C(V1)≥C(V2)，即S=C(V1)，则由二部图的性质知，C(V1)+C(V2)≥S*，从而2C(V1)≥S*，故2S≥S*。证毕。

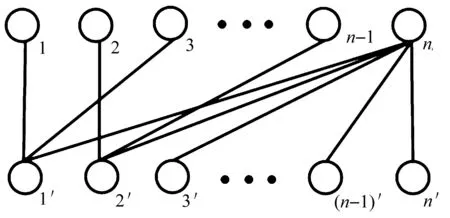
图1 算法1的紧例

2 完全二部图块上的MCISP问题

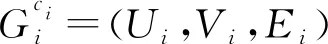
给定任意的完全二部图块Gc=(U,V,E)和颜色集C，i∈{1,2,…,n}。G中恰有3个顶点着有相同颜色且每一个Gi中的顶点颜色都不同，此时在G中找到一个独立集S并使得其中所包含的颜色种类最多。这一问题是完全二部图块上的MCISP问题。

下面给出求解MCISP问题的多项式时间近似算法。

算法2:完全二部图块上的近似算法 输入:1个简单完全二部图块Gc=(U,V,E)输出:G中包含颜色最多的独立集S步骤1:令S=ϕ,从任意的完全二部子图Gcii=(U,V,E)开始,其中i∈{1,2,…,n}。比较Gcii中的顶点集Ui和Vi,当C(Ui)≥C(Vi)时,令S=Ui,反之令S=Vi;步骤2:对每个Gcrr,比较Gcrr中Ur和Vr可在当前S中增加的颜色类,当C(Ur∪S)≥C(Vr∪S)时,令S=Ur∪S。反之令S=Vr∪S。其中r≠i,r=1,2,…,n。结束算法。

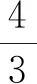
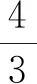
当A=∅时，S=S*，结论成立；

当A≠∅时，假设A中至少存在一个顶点αmp，使得αmp至多对应于S中2个颜色不同的顶点。其中m,t,p,q∈{1,2,…,n}，m,t表示颜色不同的顶点，p,q表示其所在二部图分支被选入集合S中的顺序。

若αmp对应于S中0个顶点，但αmp与A中至少一个顶点αtq所对应的颜色在同一个二部图分支中但p≤q，此时颜色是C(αmp)的顶点所在的原二部图分支中，除C(αmp)之外只包含C(S)中的颜色，即这些颜色在这一二部图分支之前已被选入C(S)中，则由算法2可知，C(αmp)∈C(S)与A的定义矛盾。若颜色是C(αmp)的顶点与C(S)中的颜色所在顶点均不在同一二部图分支上，则颜色是C(αmp)的顶点与颜色是C(S)的顶点在不同的二部图分支上，此时可向S中添加包含新颜色的点或者C(αmp)∈C(S)，与S是算法2的解矛盾。

若αmp对应于S中1个顶点，当αmp与A中某些顶点对应于相同颜色的顶点，同理可得，则至少有一个与αmp颜色相同的顶点所在的二部图分支，使得这个二部图分支中其它顶点的颜色已对应于A中某些顶点，即这些顶点所着颜色已被选入S。故由算法2得出C(αmp)∈(S)，与S是算法2的解矛盾。若αmp与A中所有顶点所对应颜色都不同，而C(αmp)这一颜色恰在原图中出现3次，则此时必至少有一个C(αmp)所在的二部图分支中所包含颜色均不在其中，与S是算法2的解矛盾。

若αmp对应于S中2个顶点，则C(αmp)所在原二部图分支中，要么恰有一个颜色是C(αmp)的顶点所在二部图分支，使得算法2运行到这一个二部图分支时，包含了此时C(S)中两种尚无对应的不同颜色的顶点。要么只有两种颜色是C(αmp)的顶点所在的二部图分支在当前算法2运行到这两个二部图分支时，各对应了此时C(S)中不同颜色所在的顶点。若αmp与A中某些顶点所对应的颜色相同，同理可得，则必至少有一个αmp或与αmp颜色相同的顶点所在的二部图分支中只有已选入S中的点，与S是算法2的解矛盾。当αmp与A中其它任意一个顶点所对应顶点颜色都不相同时，同理可得，与S是算法2的解矛盾。即f:A→S且A中每个顶点在对应关系f下至少映S中3个顶点，3|A|≤|S|≤|S*|。

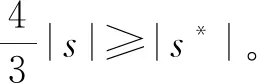
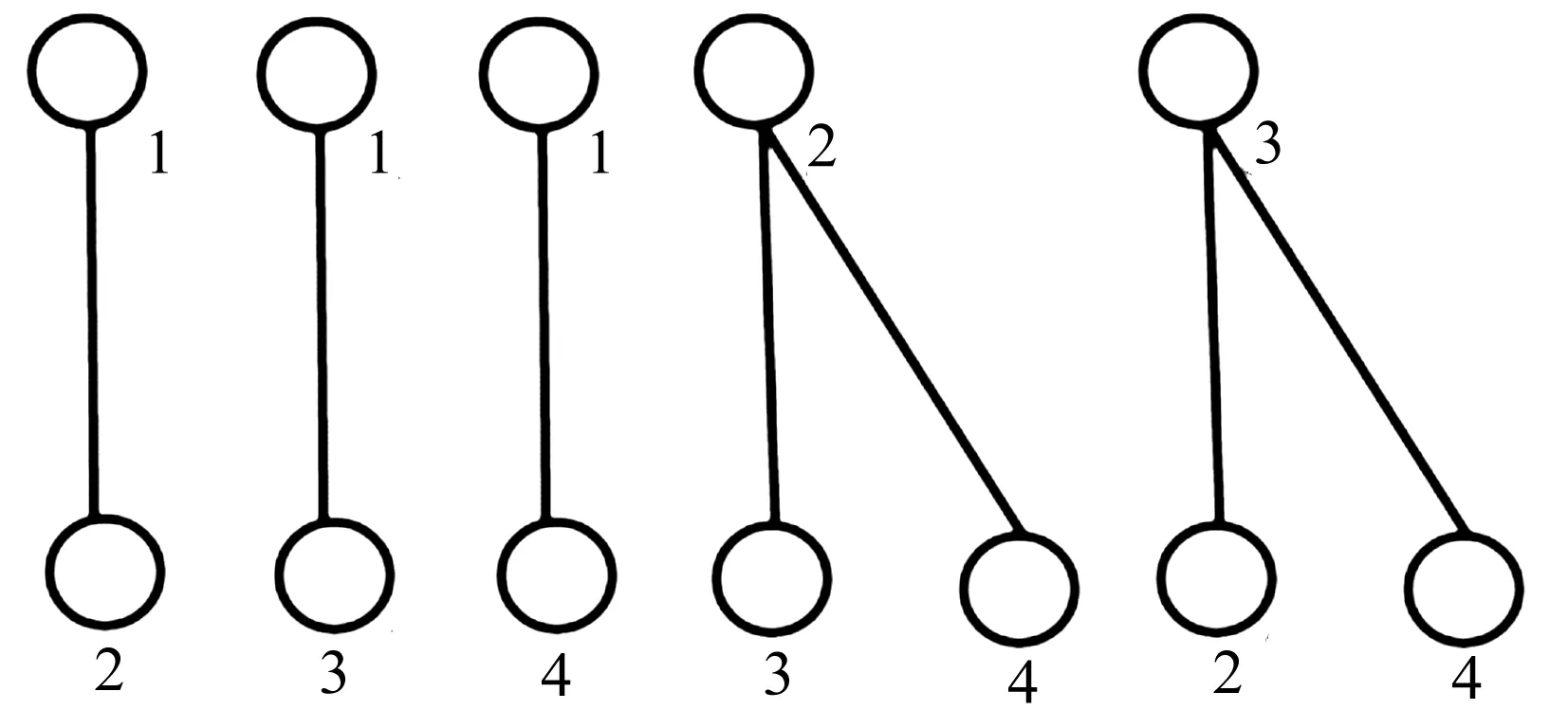
图2 算法2的紧例

3 结束语