交替方向乘子法求解混合约束二次规划问题

刘琬纯，何洪津

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

二次规划(Quadratic Programs, QP)是一类经典的数学优化模型，在工程、管理和经济等领域有着广泛的应用。在过去的几十年中，二次规划，尤其是凸二次规划的相关理论和算法得到了较完善的发展，但大规模二次规划的高效算法设计仍值得深入研究。近十年来，交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)在压缩感知、机器学习和图像处理等领域取得了诸多成功应用，在各领域掀起了交替方向乘子法的研究热潮。文献[1]给出了求解二次规划问题的交替方向乘子法。随后，有学者分析了交替方向乘子法求解二次规划时具有线性收敛速率[2]；文献[3-4]进一步分析了交替方向乘子法求解严格凸二次规划时的最优化参数选择策略。不难发现，按照文献[1]提出的交替方向乘子法框架，其线性等式约束的子问题可归结为一个增大规模的线性方程组。当线性方程组系数矩阵无特殊结构时，文献[1]中的处理方式降低了交替方向乘子法的执行效率。另外，现有交替方向乘子法解二次规划的相关文献主要讨论仅含等式和简单约束，或仅含不等式约束这两种情形。然而，现实生活中的案例可能同时具有等式、不等式和简单凸集约束条件。因此，本文针对一般的混合约束凸二次规划问题，设计新的交替方向乘子法，使得其子问题保持与原问题同规模，并且具有封闭解，从而达到提升计算效率的目的。

1 问题描述

考虑二次规划问题：

s.t.Ax=b,Dx≤d,x∈

(1)

式中，P∈n×n为对称半正定矩阵，q∈n,A∈m×n,b∈m,D∈r×n,d∈r,⊂n为简单凸集。这里简单凸集指投影到集合是易于计算的，其中投影由如下定义给出。

定义1对于给定的向量v∈n,v到凸集的投影由下式给出

本文重点考虑凸二次规划问题的求解，因此假设凸二次规划问题(1)的解集非空。

2 问题转化和交替方向乘子法

对于可分离凸规划模型：

minf(u)+g(v)

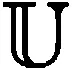
(2)

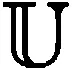
其中β>0为罚参数。给定迭代点(vk,λk)，由文献[1]可得求解(2)的交替方向乘子法迭代格式为：

(3)

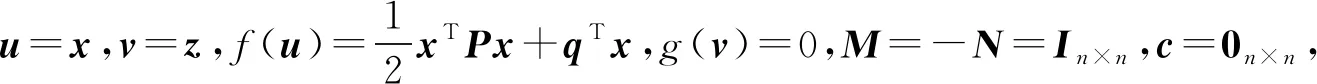
(4)

注意到式(4)中x-子问题是一个约束优化问题，可采用文献[1]给出的方法寻找(xk+1,γ)满足如下线性方程组：

(5)

显然，方程组(5)是一个增大规模的子问题，即由原问题的n维变成了(m+n)维。在这种情况下，即使系数矩阵是一个正定矩阵，理论上有封闭解，但随着A的规模增大，子问题(5)的求解代价会迅速增加。这一缺陷促使我们寻找方法降低交替方向乘子法子问题求解难度。另外，若进一步考虑凸二次规划(1)的一般形式，文献[1]的迭代格式会变得更复杂。

考虑混合约束凸二次规划问题(1)，引入松弛变量y∈将不等式Dx≤d转化为Dx+y=d。此时，令模型(2)中的且

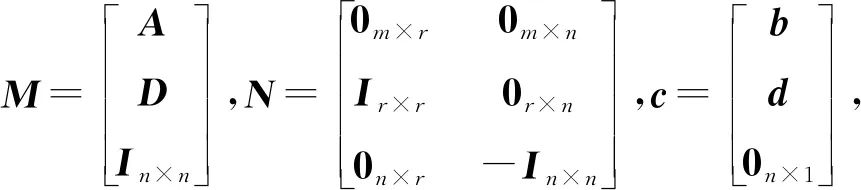
基于上述讨论，不难得到交替方向乘子法求解问题(1)的迭代格式如下：

(6)

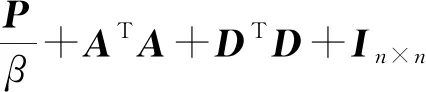
根据文献[5]中的定理4.1可知，由迭代格式(6)所产生的序列{(vk,xk,λk)}收敛到问题(1)的一个解点。特别地，已有相关文献对二次规划问题的交替方向乘子法给出了局部线性收敛速率的估计，具体见文献[2,6,7]。因篇幅限制，本文不再赘述收敛性证明和收敛速度的估计。

3 数值实验

为了进一步验证本文的交替方向乘子法(记为NADMM)在求解混合二次规划模型的有效性，分别采用3种方法进行实验，将NADMM、MATLAB优化工具包中二次规划问题的求解包quadprog(记为QUADP)和文献[1]中的交替方向乘子法(4)(记为OADMM)进行比较。

实验中QUADP采用默认设置，其精度为10-6，算法为内点法。为了保证算法的公平性，NADMM和OADMM算法的终止条件均设为

最大的迭代次数为1 000。另外，根据文献[5]的分析，罚参数β可采用自适应的方式提升交替方向乘子法的计算效率。因此，本文按如下方式调节βk+1：

(7)

其中β0=10。所有数值实验运行环境为Windows10操作系统下的MATLAB R2015b，电脑配置为Intel Corei5-4210U CPU和4GB内存。

例1考虑仅含等式和箱型约束的二次规划问题(1)，即

D=0,d=0,={x∈n|0≤x≤1}

实验中，取P=QTQ，其中Q=rand(l,n)，l取100。为了得证问题的解集非空，先随机生成x*使其元素服从均匀分布即x*=rand(n,1)，再分别令q=-Px*和b=Ax*,其中A=rand(m,n)。

例2考虑混合约束二次规划问题(1)，且

x=z,={z∈n|0≤z≤1}

实验中，取P=QTQ，其中Q=rand(l,n)，l取100。为了得证问题的解集非空，先随机生成x*,y*使其元素服从均匀分布即x*=rand(n,1),y*=rand(r,1)，再分别令q=-Px*，b=Ax*和d=Dx*+y*,其中A=rand(m,n),D=rand(r,n)。

由于例1和例2都是随机生成的二次规划问题，本文针对每一规模算例都进行10次测试，目的是为了观察算法对本类问题的稳定性。从算法的平均计算时间Time、平均迭代次数Iter和平均目标函数值Obj等3个方面进行比较，计算结果如表1和表2所示。

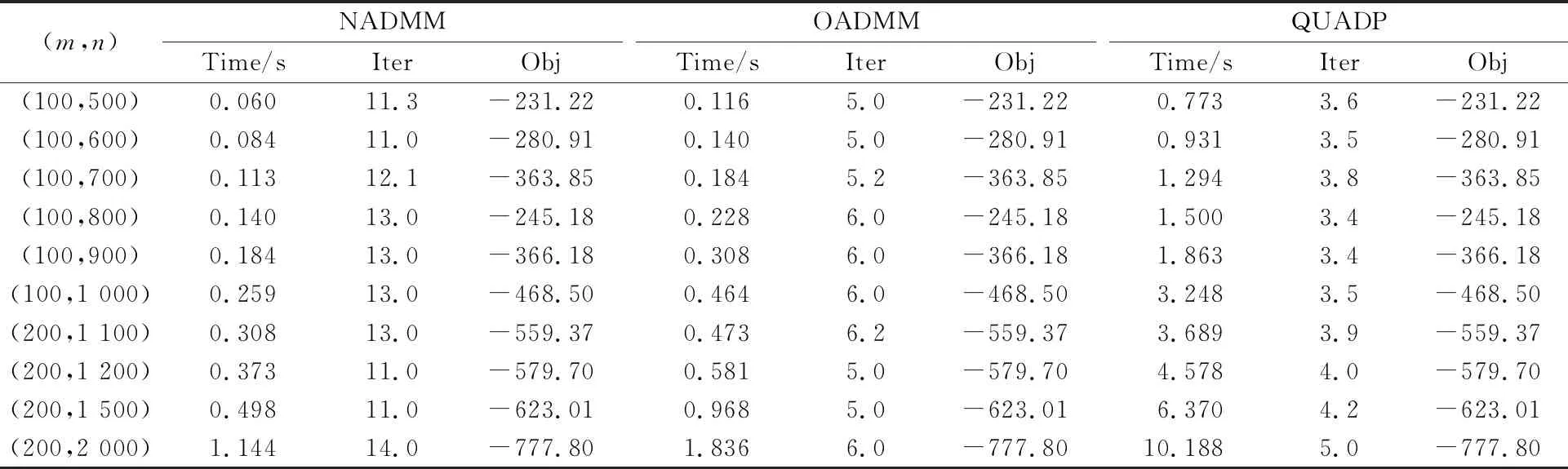
表1 3种算法求解例1的结果

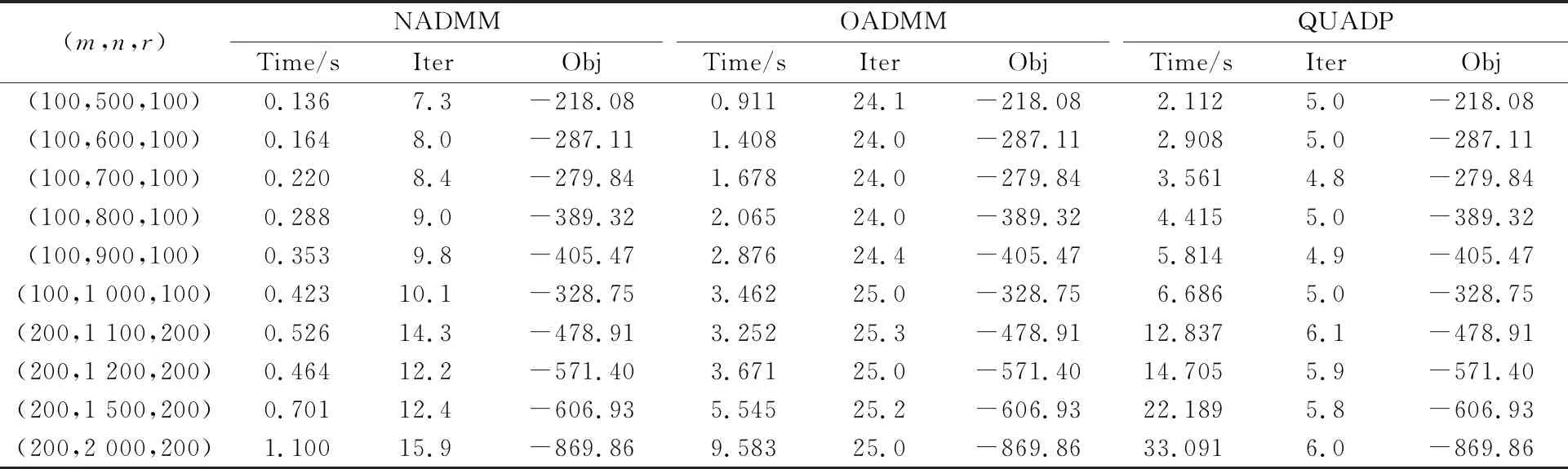
表2 3种算法求解例2的数值结果

从表1可看出，在迭代次数方面，本文提出的NADMM算法在求解例1类型的二次规划问题上比文献[1]的OADMM算法更多，但NADMM的计算时间更少。而从表2可看出，对于一般混合约束凸二次规划问题(1)NADMM在计算时间和迭代次数上都要优于文献[1]中的处理方式。另外，无论是NADMM还是OADMM，都比MATLAB中的quadprog求解函数更高效，这也说明交替方向乘子法在二次规划求解中的优势。从表1和表2的结果可以发现， NADMM比其它算法需要的计算时间更短。

为了进一步观测3种方法的稳定性，针对例1和例2其中一种情形，对3种方法进行10次随机测试，比较其运行时间，结果如图1所示。

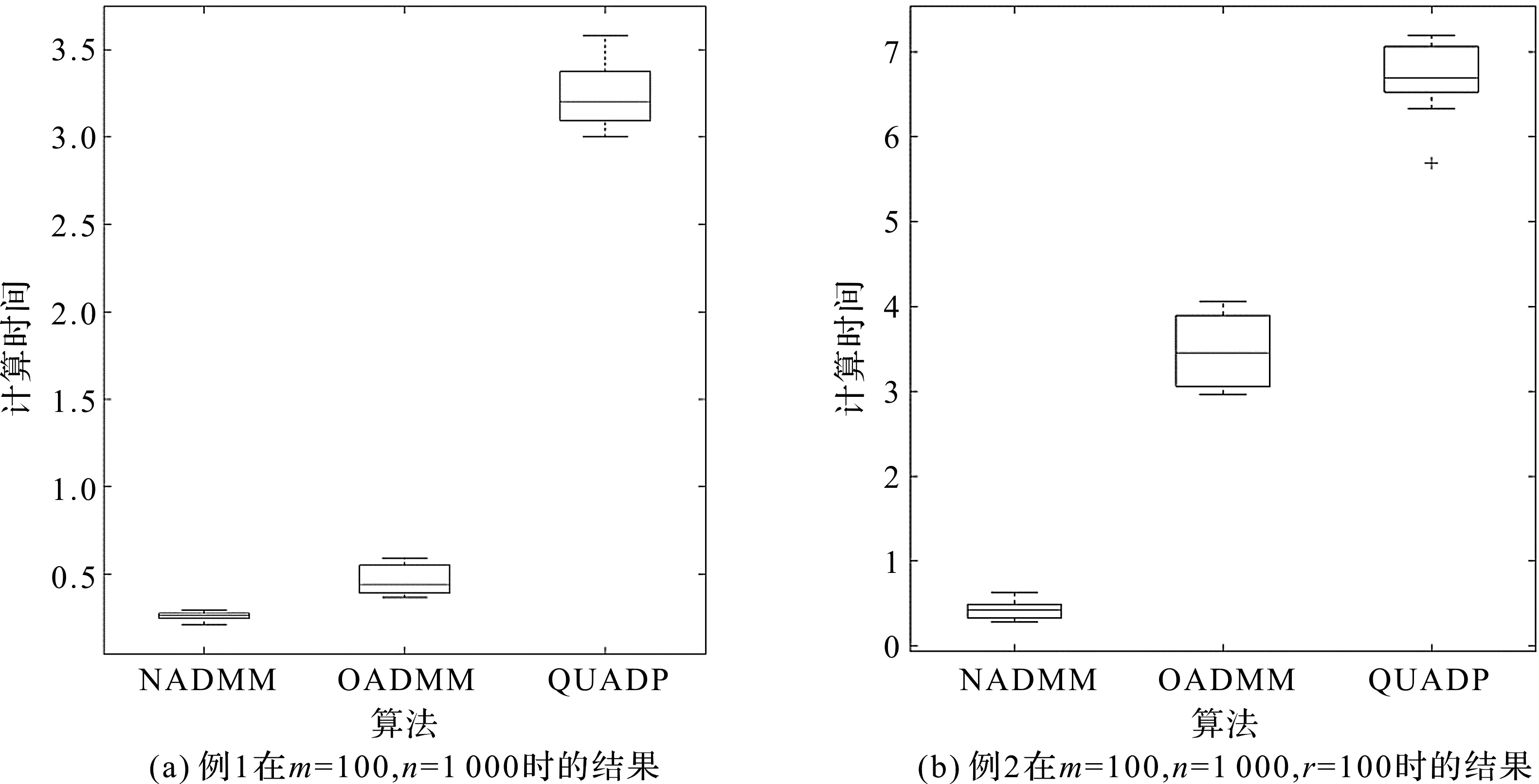
图1 3种算法求解10组随机问题的计算时间箱线图

从图1可以看出，本文的NADMM较另外2种算法有较好的稳定性。

4 结束语

针对一般混合约束的凸二次规划模型，本文提出一种改进的交替方向乘子法迭代格式，有效克服了文献[1]需求解一个增大规模的线性方程组问题的缺点，保持了每个子问题都具有封闭解形式的优势，同时，改进算法的计算时间达到最短。下一步将对非凸二次规划的交替方向乘子法设计展开进一步研究和探讨。