旋翼机双速传动系统低速档动力学建模与特性分析
陈志刚,王国强,刘志辉
(1.邵阳学院机械与能源工程学院,湖南 邵阳 422000;2.邵阳学院高效动力系统智能制造湖南省重点实验室,湖南 邵阳 422000)
0 引言
旋翼机双速传动系统是一种可以实现两档速度输出的变速系统,广泛应用于民用运输工具、精密设备、武器装备等。行星齿轮传动系统的非线性特性研究主要从建模方法、求解方法、稳定性判断等3 个方面展开研究。模型主要有纯扭转模型、弯扭耦合模型和扭摆横向轴向耦合模型[1-3],其中对于纯扭模型只考虑各构件扭转方向的振动,由于自由度较少,模型简单,故又称之为精简模型,数学建模过程中一般只考虑齿侧间隙、时变啮合刚度和综合啮合误差。孙涛[4]等在考虑纯扭转的情况下建立了ZK-H 行星轮系非线性动力学方程,通过谐波平衡的方法分析了系统的频域特性;宋轶民和许伟东[5]等建立了ZK-H 型行星齿轮传动的修正扭转模型并研究了其固有特性。
基于非线性动力学模型,为了对行星齿轮传动系统有一个直观的了解,XIANG L 等[6]通过全局分岔图、Poincare图、相图、FFT 谱和最大李亚普诺夫指数对行星轮系系统的非线性动力学特性进行了分析。XIANG L 等[7]通过全局分岔图、最大李亚普诺夫指数(LLE)、Poincare 图、相图、FFT 谱和时间序列等方法,识别了系统运动对侧隙变化的影响。周璐等[8]通过相轨线、Poincare 图、时间历程曲线和相轨线分析了齿侧间隙、啮合频率和啮合阻尼对系统分岔与混沌特性的影响。
通过对纯行星齿轮传动系统非线性特性较为深入的分析后,本研究拟针对旋翼机双速传动系统,研究低速档在档状态,采用集中参数法建立考虑时变啮合刚度、齿侧间隙和齿轮副综合啮合误差的纯扭非线性动力学微分方程组,然后利用变步长四阶龙格库塔法对无量纲化微分方程组进行求解,定性分析激励频率对旋翼机双速传动系统非线性动态特性的影响规律。
1 低速档非线性动力学模型
限于篇幅本次以双速行星传动系统低速档为对象,建模时假设各传动轴和轴承刚度足够大,且不考虑运动状态下支撑轴承间的摩擦影响;同级同类型的行星轮各参数相同;齿轮副之间的啮合状态简化为由弹簧相连接的圆柱体,弹簧的刚度系数为啮合齿轮的啮合刚度[9]。以图1 所示的工况为对象,采用集中质量法建立动力学模型进行建模和详细分析。

图1 旋翼机双速传动系统低速档在档动力学模型
图中Rbs为太阳轮基圆半径;Rp1为第一级行星齿轮的基圆半径;Rp2为第二级行星齿轮的基圆半径;Rbr1为内齿圈的基圆半径;TD为驱动力矩;TL为负载力矩;JC为行星架转动惯量;θc为行星架扭转变形;Ksp1为太阳轮与第一级行星轮时变啮合刚度;Csp1为太阳轮与第一级行星轮啮合阻尼;Kp1p2为第二级行星轮与第一级行星轮时变啮合刚度;Cp1p2为第二级行星轮与第一级行星轮啮合阻尼;Kp2r1为内齿圈与第二级行星轮时变啮合刚度;Cp2r1为内齿圈与第二级行星轮啮合阻尼。
2 双速传动系统低速档在档数学模型
定义Xsp1i、Xp1ip2i、Xr1p2i分别为齿轮副沿啮合线方向上的动态相对扭转位移。根据啮合状态的各齿轮的相对位置关系,计算各齿轮间的相对位移:
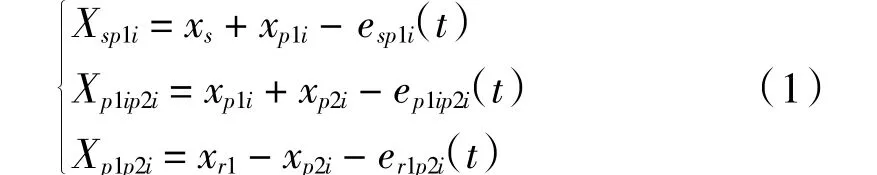
式中:ei为齿轮副综合啮合误差,一般假定按正弦函数变化[4]:
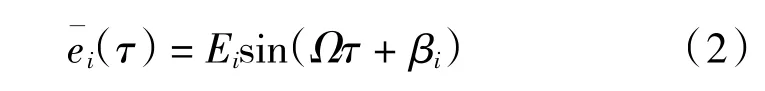
式中:Ei为各齿轮副的综合误差的幅值;βi为各齿轮副综合啮合误差的初相位;Ω为轮系啮合齿频;t为时间。假设令xs=Rbsθs、xp1i=Rbp1iθp1i、xp2i=Rbp2iθp2i、xr1=Rbp1θr1,其中xs、xp1i、xp2i和xr1分别为太阳轮、行星轮1、行星轮2、内齿圈的当量线位移。由牛顿第二定律推导得到旋翼机双速传动系统低速档在档运动微分方程:

式中:Ci为齿轮副的啮合阻尼。如:
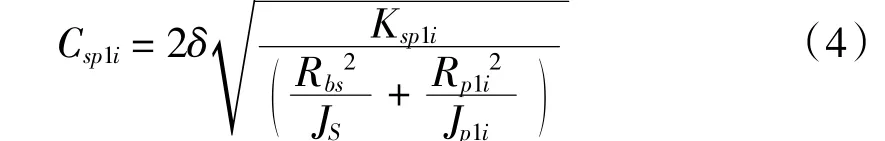
f(X,b)为齿侧间隙非线性函数如下:
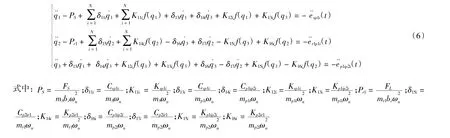

3 激励频率影响规律
本研究的结构参数见表1,图2 为旋翼机双速传动系统低速档模式下,以激励频率ωh为控制变量绘制的太阳轮和第一级行星轮形成的齿轮副a 的无量纲化位移分叉图。由图3 可知齿轮副a 在ω=0.62 和ω=0.78两处存在明显的跳跃现象;当激励频率位于0.62≤ω≤0.78 段时,齿轮副a 以不太稳定的周期形式运动;当激励频率处于低频段(ω≤0.62)时,齿轮副a 随着激励频率ω的增加,振动幅度差会有轻微的增大的趋势;当激励频率处于中低频段(0.78≤ω≤1.19)时,齿轮副a 由单周期响应随着激励频率ω的增加,振动幅度差明显增大,有进入混沌的趋势;当激励频率处于中频段(1.19≤ω≤1.41)时,齿轮副a 的运动表现为,随着激励频率的增大,齿轮副a 由双倍周期响应转向三倍周期以及多倍周期,从图3-b 部分时域图可以看出,再进入混沌期前转为双倍周期;当激励频率位于(1.41≤ω≤2.61)时,齿轮副a 进入了混沌区,从图3 中的c 部分相图可以看出,线条充满空间某一部分、相互缠绕交叉,既不重复又不封闭的曲线,当激励频率位于(2.61≤ω≤2.82)时,系统的运动从双倍周期向单倍周期变化,从图3-d 部分时域图可以看出;最后激励频率位于(2.82≤ω)时,齿轮副a 为单倍周期响应。图3 为激励频率点ω, 其取值分别为:0.612,1.023,1.923,2.712 时系统的时域图、相图和庞加莱截面图。
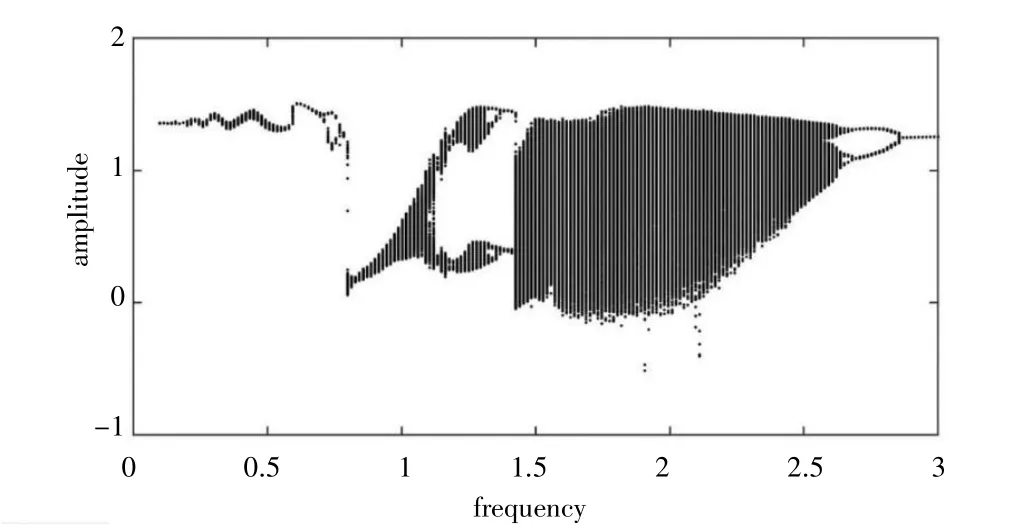
图2 太阳轮和第一级行星齿轮形成的齿轮副a 随激励频率ω 变化的全局分叉图
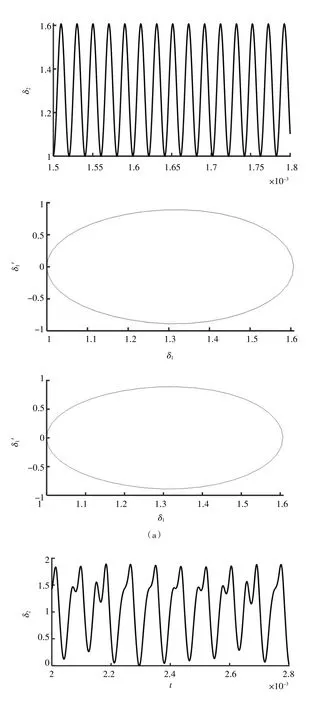
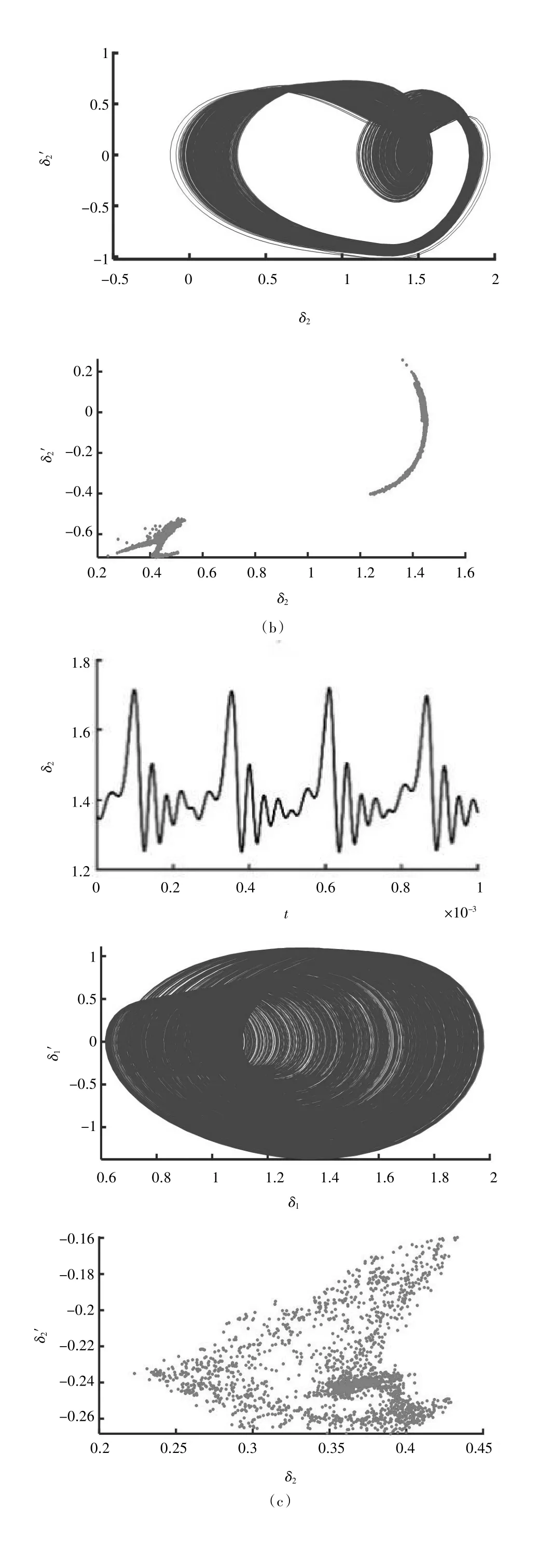
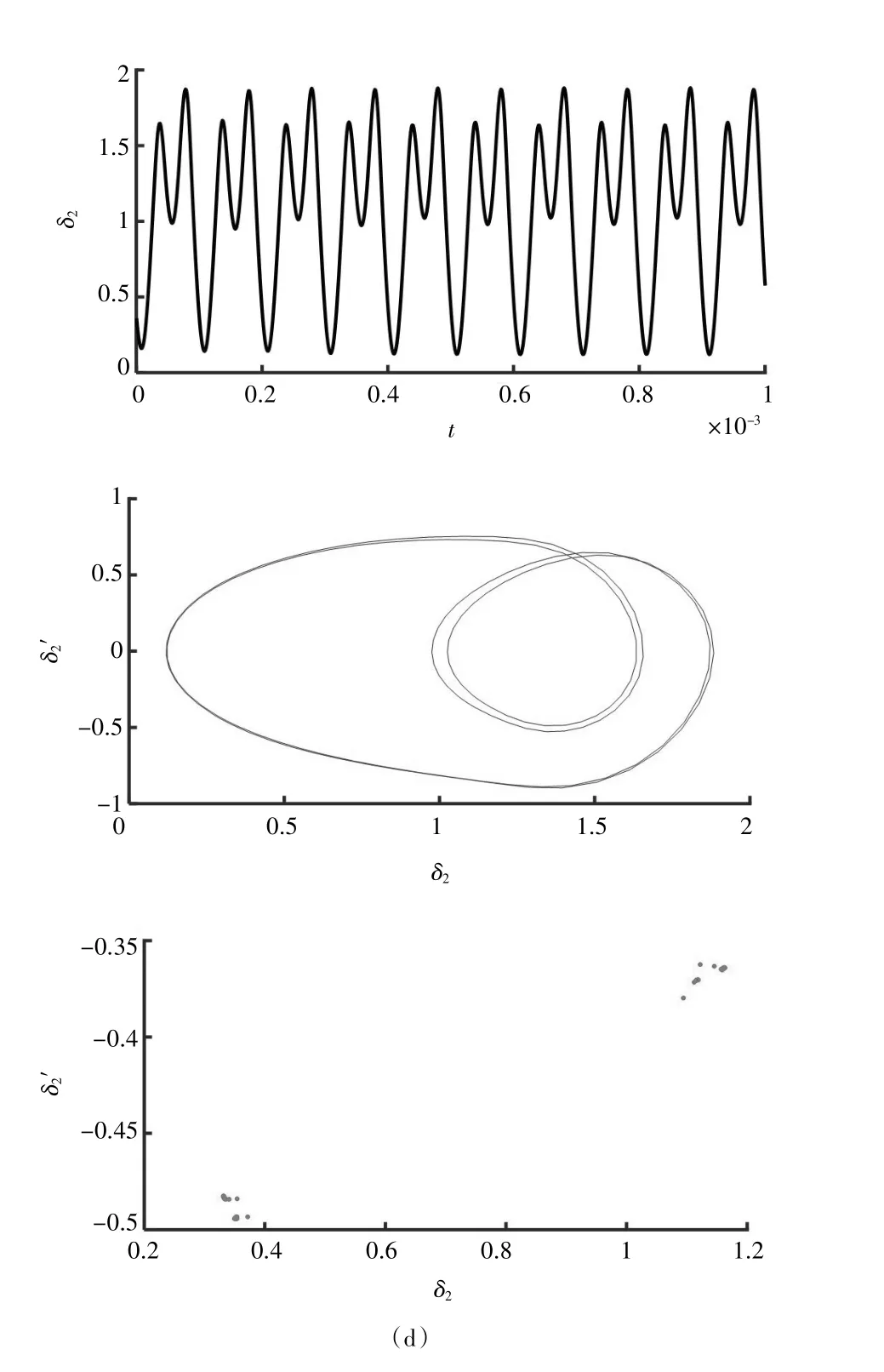
图3 齿轮副a 不同激励频率点对应的时域图、相图和庞加莱截面图:(a)0.612;(b)1.032;(c)1.923;(d)2.712

表1 旋翼机双速传动系统低速档模型参数
4 结论
本研究在考虑时变啮合刚度、齿轮副综合啮合误差和齿侧间隙的基础上建立了旋翼机双速传动系统低速档在档的非线性动力学模型,用数值仿真的方法对系统方程进行求解,得到太阳轮和第一级行星齿轮形成的齿轮副a 随激励频率变化的分叉图,由分叉图再结合不同区域的激励频率展现出的时域图、相图和庞加莱截面图,结果表明,在激励频率位于(0≤ω≤3)范围内,位于低频段时,系统的振动响应幅值变化不大;主要变化在中频段(0.78≤ω≤2.82)内,随着激励频率的增大,系统由单倍周期响应逐渐从双倍周期响应进入多倍周期响应,再由双倍周期响应进入混沌响应,最后在激励频率为(2.61≤ω≤2.82)时段,系统由混沌响应进入双倍周期响应再转为单周期响应。

