四轴陀螺组件突变故障的检测与隔离
胡晓强, 张霄力, 彭侠夫
(厦门大学 航空航天学院,福建 厦门 361101)
在联邦滤波结构的组合导航系统中,惯性导航系统(likelihood ratio method,INS)作为公共参考系统,与其他辅助导航系统组成滤波子系统[1]。许多文献假设INS系统工作的可靠性具有绝对保证,重点分析INS系统对其他导航子系统故障检测与识别(FDI)的辅助方法[2]。惯导系统的可靠性直接影响到航行体的可靠性,因此提高惯导系统的可靠性对于提高航行体的生存能力具有重要意义[3]。
惯性导航系统常采用余度技术为其容错设计提供硬件基础[4],器件级冗余技术在提高可靠性和控制成本等方面,较系统级冗余技术具有较大优势。针对冗余惯性测量组件(RIMU)的故障诊断,常采用基于等价空间原理的最优奇偶向量法(OPT),广义似然比法(GLT)与奇异值分解法(SVD)。许多文献将模糊决策[5]、支持向量机[6]、主成分分析[7-8]、小波变换[9]、滤波器[10-11]等方法引入RIMU故障诊断中,对基于奇偶空间的算法进行改进与扩展。
在不显著增加系统成本的前提下,4个陀螺组成的冗余配置方案比无冗余系统的可靠性高1.75倍[12]。因此,四陀螺冗余惯性测量组件在民用设备和常规武器上具有重要的研究价值。但是在仅存在1个余度的情况下,传统的奇偶空间法只能检测出故障,而不能对故障仪表进行正确隔离。王晨等[13]针对运载火箭双捷联系统,基于多个并行反向传播神经网络(BP)的预测结果,实现三度陀螺故障的分离,但神经网络观测器的设计需要控制指令作为额外输入。李勇等[14]使用小波包分解提取陀螺的能量特征,结合支持向量机分类器进行陀螺的故障诊断,但提出的算法只适用于平稳过程,无法区分载体的正常机动与故障。De Oliveira等[15]针对光纤陀螺的最小冗余配置,使用小波包变换获得奇偶向量的能量分布,通过计算噪声高频能量在残差空间的投影大小进行故障辅助分离。程建华等[16]研究了五轴RIMU双故障并发的容错问题,采用线性估计的方法辅助GLT算法对陀螺器件进行故障分离。吴唯强等[12]使用小波变换检测陀螺信号的突变时刻,结合GLT的检测结果实现四轴RIMU的故障诊断。但由于没有考虑GLT的故障检测延时,上述2个方法仅适用于较大的突变故障。
本文针对四轴陀螺组件中故障器件的识别问题,提出一种基于广义似然比法与斜率突变检测相结合的两级故障诊断方法。该方法通过残差广义似然比法实现四陀螺RIMU的故障检测;在检测出故障的情况下,根据陀螺的输出数据拟合信号斜率。以陀螺输出数据的斜率变化定位故障器件,从而使得四陀螺RIMU发生故障的情况下,能够准确地识别故障器件,进行有效的器件隔离和输出重构,提高惯性导航系统陀螺组件的精度和可靠性。
1 四轴陀螺冗余配置分析
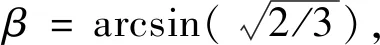
(1)

(2)
陀螺组件的冗余测量方程可表示为:
V=Hω+ε
(3)
式中:V∈R4为陀螺的量测数据;ω∈R3为待测的系统角速度;H是陀螺的测量矩阵;ε∈R4是均值为0、方差为σ2I4的高斯白噪声序列;σ为噪声标准差;I4∈R4×1表示元素数值为1的向量。
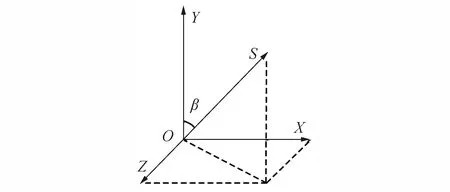
图1 三正交一斜装配置Fig.1 Three orthogonal one oblique configuration

图2 锥面斜置配置Fig.2 conical surface configuration
(4)

(5)

(6)
式中:Fp为陀螺组件的量测性能指标,其数值越小,表明陀螺组件输出中所包含的噪声越小。
四轴RIMU共有5种输出模式:123、124、134、234与1234,其数字对应于测量矩阵中的行向量。三正交一斜装配置与锥面斜置配置2种输出形式的量测性能如表1所示。
由表1可见,当所有陀螺正常工作时,配置2在1234模式下将取得最优的量测性能;当四轴RIMU的某一陀螺因故障被隔离后,配置2的量测输出在3种模式下(分别为124、134与234)优于配置1的对应输出,若每个陀螺的故障概率相同,则配置2的量测性能在一次故障条件下有75%的概率优于配置1。

表1 四轴RIMU配置的量测性能Table 1 Measurement performances of gyro-quadruplet
当四轴RIMU的某一陀螺发生故障,组件的冗余测量方程为:
V=Hω+ε+F
(7)
式中:F为陀螺故障向量,故障器件对应的元素为f,其他元素为0。使用解耦矩阵U获得的奇偶残差r为:
r=UV=Uε+UF
(8)
利用Potter算法分别求取2种配置方法的解耦矩阵为:
(9)
(10)
以器件某一量级大小的故障f与奇偶残差噪声标准差的故障噪声比衡量器件的故障检测性能,定义冗余组件的故障检测性能为:
Ffdi=uif/σr,i=1,2,3,4
(11)
(12)
式中:Ffdi(i=1,2,3,4)分别为4个陀螺的故障检测性能;Ffd为整个陀螺组件的故障检测性能,其数值越大表示陀螺组件的故障检测性能越好;ui为解耦矩阵U中的对应元素;σr为奇偶残差的噪声标准差。2种配置方案奇偶残差的故障检测性能如表2所示。可见,配置2的故障检测性能更好。

表2 四轴RIMU配置的故障检测性能Table 2 Fault detection performances of gyro-quadruplet
根据上述分析,为了获取最优的数据输出量测性能与故障检测性能,本文选取配置2(锥面斜置配置)作为四轴陀螺组件的配置方式。
2 基于斜率突变辅助的故障诊断方法
2.1 基于斜率突变检测的故障隔离方法
根据广义似然比法(GLT)检测到故障后,需要准确地识别故障器件,才能有效地进行故障器件的隔离和输出重构。当陀螺仪工作正常时,由于载体角运动的连续性,在足够小的时间段内,陀螺仪测量输出序列的拟合斜率近似于1个常值;当陀螺仪出现故障时,陀螺仪测量输出值将呈现不连续性,其拟合斜率将在短时间内发生明显的变化。
设定陀螺仪的量测输出序列为:
ρi(t)=[vi(t-c1+1),vi(t-c1+2),…,vi(t-1),vi(t)]
(13)
式中:ρi(t)(i=1,2,3,4)为第i个陀螺在t时刻获得的测量输出向量;vi(t)为第i个陀螺在t时刻的测量输出;c1为ρi(t)的序列窗口长度。为了降低量测噪声的影响,以整数序列τ=[1,2,…,c1]为自变量,陀螺量测输出序列ρi(t)为因变量,使用最小二乘法将c1个数据对拟合为直线,则目标函数为:
(14)
式中:a、b分别为直线的斜率与截距。记a为Gi(t),则:
(15)
当第i个陀螺器件在t时刻发生故障,其拟合斜率Gi在故障后的一段时间内呈现出先增大后减小的变化趋势。但由于陀螺输出噪声的影响,Gi的数值围绕着变化趋势上下波动。为了增强斜率变化趋势,计算陀螺输出序列的拟合斜率增量:
(16)
(17)

Δηi(t)={ΔGi(t-c3+1),…,ΔGi(t-1),ΔGi(t)}
(18)
式中:c3为增量序列的时间窗口长度。则陀螺器件的故障判定原则:

(19)
式中:φ={ΔGi(j)|ΔGi(j)∈Δηi(t)&ΔGi(j)>TI};TI为预先设置的阈值;∅表示空集。
2.2 陀螺组件的故障诊断与重构方法
当载体由于机动运动产生姿态变化时,陀螺的正常输出数据与故障情况的输出在信号特征上具有高度的相似性,使用斜率突变检测的方法将难以区分机动运动和故障。因此,基于斜率突变检测的故障诊断方法,需要结合整个陀螺组件的故障检测结果对四陀螺组件进行复合诊断。本文提出的斜率突变辅助故障诊断算法(slope mutation assisted fault diagnosis algorithm,SAD)采用广义似然比法判断冗余陀螺组件是否发生故障,若系统发生故障,采用斜率突变的故障隔离方法判断冗余系统中的哪个陀螺发生故障,其组合方案流程图如图3所示。
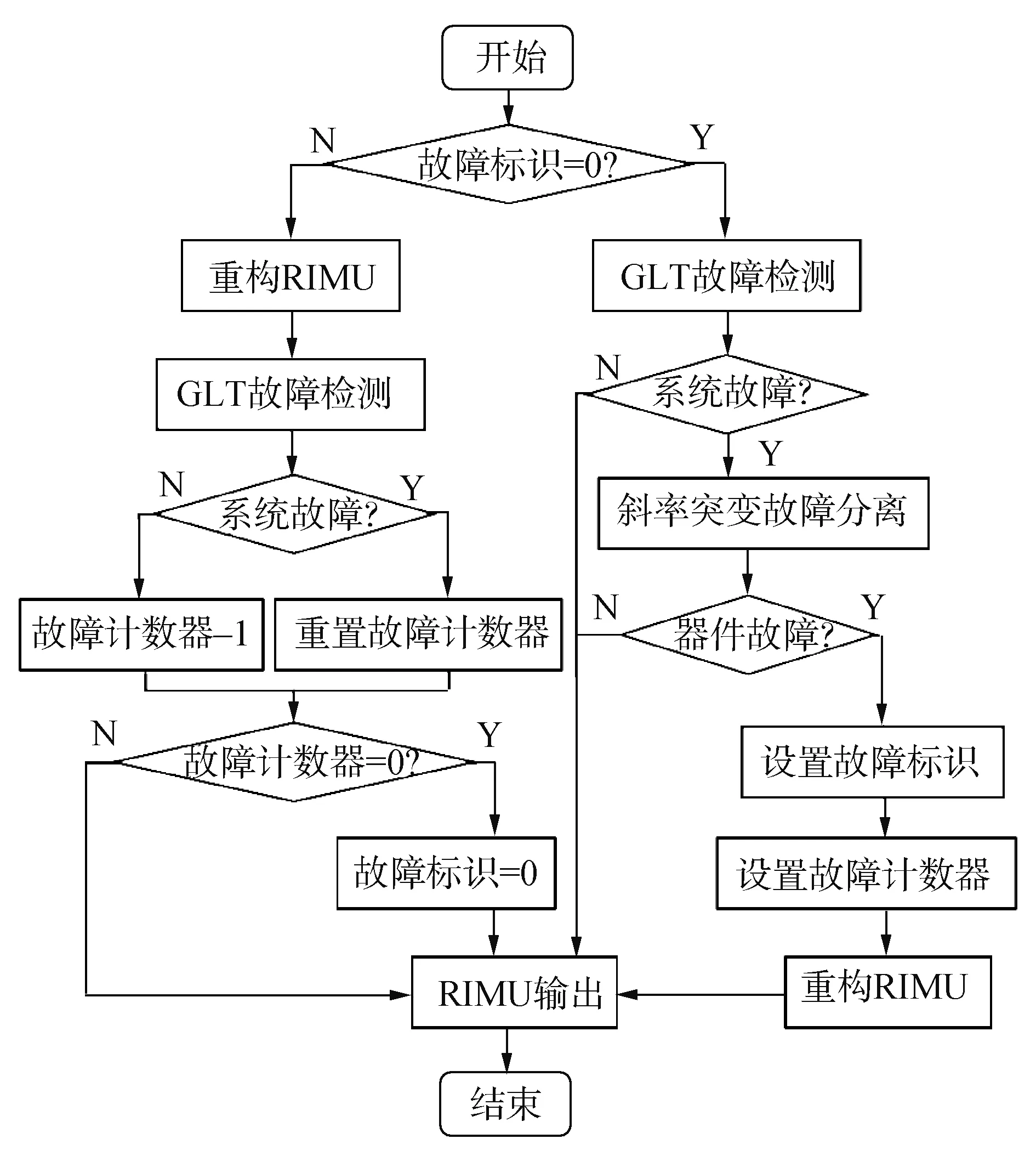
图3 斜率突变辅助故障诊断算法流程Fig.3 Flow chart of SAD algorithm
在隔离故障陀螺后,需进行系统重构并更新陀螺的测量输出,使其不含有故障信息。假设t时刻通过广义似然比法判断系统发生故障并采用斜率突变方法隔离出故障陀螺k,构建故障信息矩阵W,进行系统重构:
(20)
式中:故障信息矩阵W为m×m维矩阵,当系统无故障时,W为单位矩阵,当系统隔离第i号陀螺,则W的第i行设置为零行。
根据上述设计的故障隔离和重构方案进行诊断
后的处理,在损失一定精度的条件下,可以确保四轴RIMU输出不受故障影响,实现陀螺组件一次故障正常工作的容错能力。
3 故障检测与隔离仿真
3.1 算法性能分析
为了验证本文所提出算法的有效性,建立数字模拟平台,故障检测与隔离仿真条件如下:
1)选取四轴陀螺组件在某一6 s内的输出作为算法性能验证数据,其中前2 s为平稳输出过程,后4 s为机动运行过程;
2)RIMU中的陀螺仪的噪声标准差为0.5(°)/h1/2,数据输出频率为100 Hz;
3)整个陀螺组件的故障检测方法采用窗口长度n=6的固定历元检验法设置了2个故障检测阈值进行对比;斜率突变分离法参数分别为c1=30、c2=4和c3=50,故障分离门限为TI=0.08σ;
4)仿真实验在个人电脑上进行,CPU为i5-8265U,频率1.60 GHz,内存为8 GB。
定义如下性能指标:虚警率为无故障情况下故障诊断算法判定某陀螺故障的概率;漏检率为算法在故障持续时间内没能定位故障器件的概率;误警率为故障存在情况下,诊断算法错误定位故障器件的概率;检测延时为算法正确定位故障器件所使用的故障数据个数;诊断耗时为诊断算法对数据输入进行1次完整的检测、分离所花费的时间。
从第3 s开始分别在4轴上加入不同大小的突变故障,分别使用本文提出的SAD算法与文[16]中的线性估计辅助算法(LSG)进行故障诊断,每种情况重复试验100次,当判定某器件故障时停止该次试验。记录程序每次试验最后一个数据的诊断时间,计算算法平均诊断耗时。为了分析对比2种辅助诊断算法的性能差异,LSG采用相同的FSS算法作为整个RIMU系统的故障检测算法。其中x轴陀螺的实验结果如表3所示。

表3 X轴陀螺的故障检测结果Table 3 Detection result of X-axis faults
由模拟结果可知:
1)阈值TD越大,FSS的虚警次数就越小,同时对于突变故障的平均检测延时就越大;
2)对比TD=19.905时LSG算法与SAD算法的虚警率:只要FSS检测法虚警就将造成LSG算法的虚警;而SAD算法由于器件级算法也采用阈值比较,其最终检测结果未必虚警,这使SAD的虚警率比LSG的虚警率低了19%~32%;
3)对比小故障情况的“漏检次数/误检次数”,采用阈值比较的SAD可能因为不能分离小故障而出现漏检,而选取最大值的LSG则因误检将正常器件从陀螺组建中分离;
4)在仿真实验设置的阈值TD下,LSG算法对4σ突变故障的检测次数分别为16与26次,而SAD算法在TD=26.540时仍有44次试验检测出3σ故障,在TD=19.905时仍有34次试验检测出3σ故障,更加适用于小幅值故障的检测;
5)在TD=19.905时,SAD算法在每组试验中分别出现2~5次虚警,当将试验数据换成平稳过程时该现象消失,这说明该现象是由于2 s时载体的爬升过程造成FSS检测法的虚警,进而造成SAD算法的虚警;
6)相比于LSG算法,SAD算法的计算复杂度偏高,在仿真试验条件下,其完成一次检测与分离的时间约为0.04~0.1 s。
综上所述,LSG算法由于没有考虑突变故障的检测延时,并且通过选取线性预测误差最大的陀螺作为故障器件,因此容易出现虚警与故障器件错误分离的情况,而SAD算法虽然计算复杂度较高,但在绝大多数情况下都能够快速准确地实现较大故障的检测与分离,并且对小幅值故障具有一定的诊断效果。
3.2 INS/GPS容错导航模拟验证
在上述仿真参数基础上增加如下仿真条件:
1)固定翼飞行器的仿真轨迹包括加速、爬升与协调转弯等机动动作,仿真时长总共436 s;
2)载体的初始姿态为[0, 0, 0]T,初始失准角分别为30″、-30″、20′;初始速度为0。初始速度误差为0.1 m/s;初始位置为东经58.91°、北纬50.25°和高度380 m,初始位置误差为[2,2,5]T(m);
3)GPS提供位置信息,其水平位置量测误差与高度量测误差分别服从标准差为2 m和5 m的高斯分布,数据输出频率为1 Hz;
情景1:FSS的阈值TD=19.905,故障计数器的初值为10,故障参数设置如表4所示。
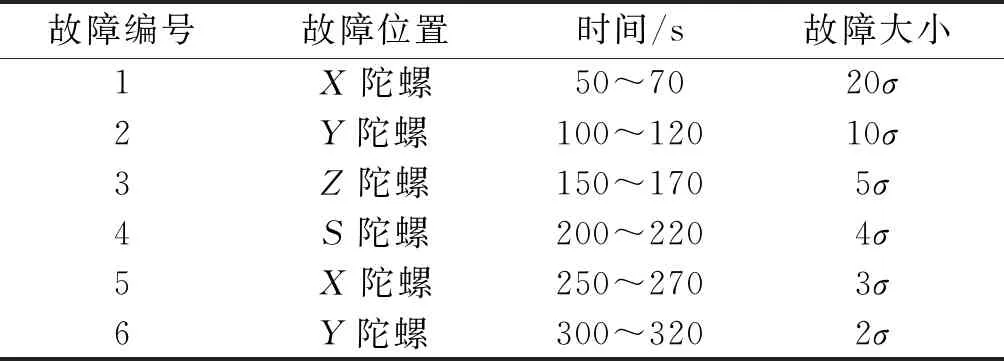
表4 情景1中注入的故障信息Table 4 The fault information injected in scenario 1
分别使用本文提出的SAD算法与线性估计辅助算法对陀螺组件进行故障诊断与系统重构,并将载体的导航位置信息与载体的真实位置进行对比。多次重复试验的结果大体相似,其中1次的实验结果如图4所示。
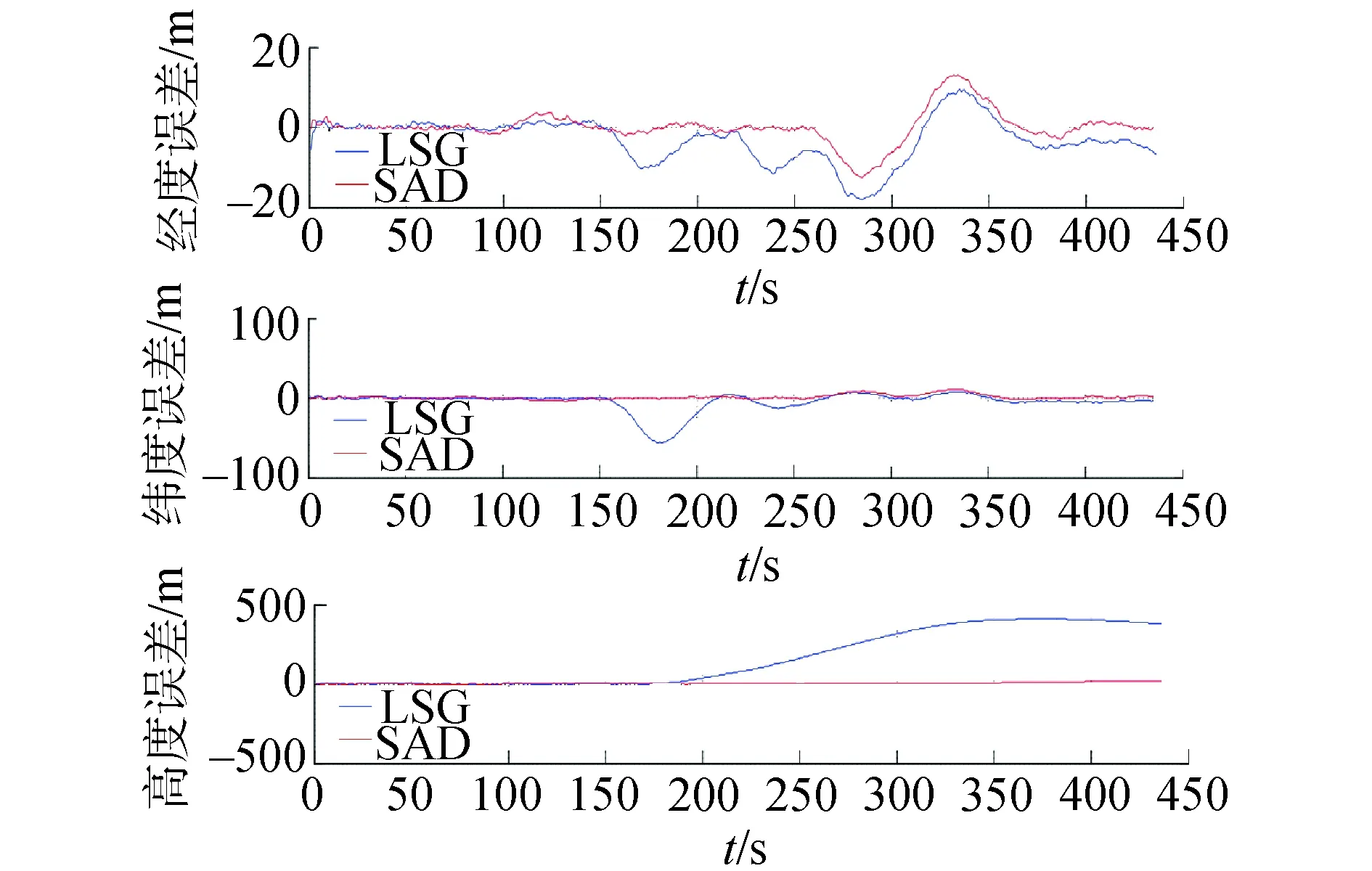
图4 SAD算法与LSG算法的组合导航位置误差对比Fig.4 Comparison of position errors between integrated navigations using SAD or LSG
由图4可知,在20σ与10σ等较大突变故障情况下,LSG算法与SAD算法都能够实现四轴陀螺组件的故障诊断与重构,保证组合导航输出不受故障陀螺的影响;在本次实验中,LSG算法无法实现陀螺组件在5σ突变故障的正常输出,因此其导航误差从150 s开始发散;而SAD算法从3σ突变故障开始引入故障信息,影响组合导航系统的正常输出,但其保留了所有正常器件参与角速度估计,降低了微小故障的影响程度,最终的高度误差在25 m内。
情景2:FSS的阈值TD=26.540,故障计数器的初值为20,故障参数设置如表5所示。
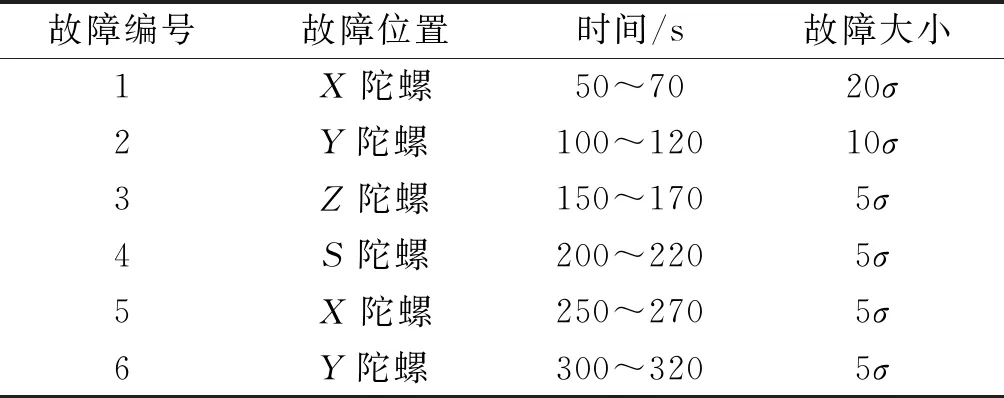
表5 情景2中注入的故障信息Table 5 The fault information injected in scenario 2
分别使用本文提出的SAD算法与LSG进行故障诊断,并将载体的导航位置信息与载体的真实位置进行对比,实验结果如图5和图6所示。
由图5与图6的仿真结果可知,LSG算法与SAD算法都能够保证组合导航系统的陀螺组件不受10σ以上突变故障的影响;在本次实验中,使用LSG算法的组合导航系统受到5σ故障的影响,导航位置误差发散;而使用SAD算法的组合导航系统,在4次5σ突变故障情况下均能对故障器件进行准确定位,并实现有效的隔离与处理,保证在任何一个陀螺发生故障的情况下组合导航系统的正常运行。
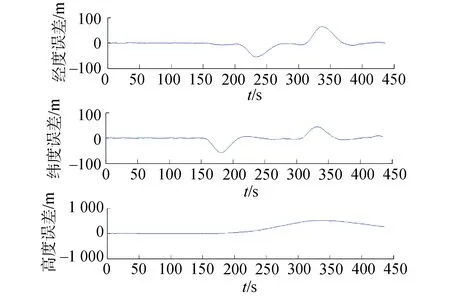
图5 LSG故障容错情况INS/GPS组合导航位置误差Fig.5 Position error of INS/GPS system using LSG

图6 SAD故障容错情况INS/GPS组合导航位置误差Fig.6 Position error of INS/GPS system using SAD
4 结论
1)SAD算法采用两级的阈值诊断方式,相对于LSG算法降低了19%~32%的虚警率;
2)SAD算法能够准确识别3σ以上的突变故障,相对于LSG算法具有更高的故障灵敏性;
3)SAD算法在小故障情况下具有更低的误检率,避免了陀螺组件正常器件的错误隔离。
SAD算法能够快速准确地识别具有更低幅值的突变故障,实现故障器件的准确定位和有效处理,提高了惯性导航系统陀螺组件在最小冗余配置条件下的精度和可靠性,对于保证冗余式捷联惯导系统的可靠性具有重要的实际意义。

