基于CIES-CA的水声阵列多目标方位估计技术
王辛, 郭龙祥, 生雪莉, 殷敬伟, 李佳馨
(1. 哈尔滨工程大学 水声技术重点实验室,黑龙江 哈尔滨 150001;2. 海洋信息获取与安全工业和信息化部重点实验室(哈尔滨工程大学),黑龙江 哈尔滨 150001;3.哈尔滨工程大学 水声工程学院,黑龙江 哈尔滨150001)
传统的水声方位估计中,通常使用的是均匀直线阵列结构,但由于水声探测环境多目标、多干扰的特点,为了有效地分辨目标,对阵列的空间分辨力有一定的要求。而阵列的空间分辨力与阵列孔径直接相关,对于均匀直线阵列而言,为了避免角度模糊,阵元间距限制在分析信号频率上限的半波长以下,在这种条件下要想获得高的空间分辨力就需要大量的阵元组成长线阵[1]。但是出于对制造成本以及信号处理实时性等方面的考量,实际的水声阵列使用过程中不便使用过多的阵元通道数据。为了解决这一问题,诸多学者研究如何使用较少的阵元数完成对多目标方位的高分辨估计。为此,许多稀疏阵型结构被提出,Moffet[2]提出了最小冗余阵的概念,但由于其结构不唯一导致实际应用中的不便。Vaidyanathan等[3]提出由2个子阵组成嵌套阵列的概念,但由于第一子阵的阵元间距较近容易受互耦效应影响而存在缺陷[4]。Vaidyanathan等[5]又提出了互质采样和互质阵(coprime array, CPA)的阵列模型概念。此后提出的改进的互质阵结构通过对子阵压缩平移获得新的互质阵结构(coprime array with compressed inter-element spacing, CIES-CA)[6],减少了互质阵虚拟阵列损失的孔径影响。
为此,本文站在水声多目标方位估计的背景上,利用信号分类算法与虚拟阵元法,从多目标方位分辨能力以及多目标方位估计误差2个方面,分析子阵压缩的互质阵在多目标估计中的算法性能。并通过实验数据处理验证子阵压缩互质阵的有效性和高分辨能力。
1 基于子阵间距压缩的互质阵列
从阵型以及虚拟阵元法角度描述子阵间距压缩互质阵的基本原理,为下文对比常规均匀直线阵列、原型互质阵以及子阵间距压缩互质阵的多目标方位估计能力提供理论基础。
1.1 互质阵列结构
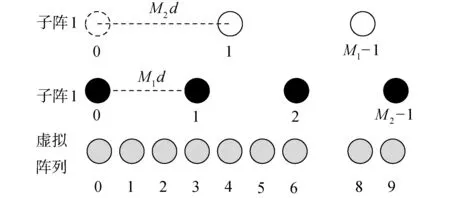
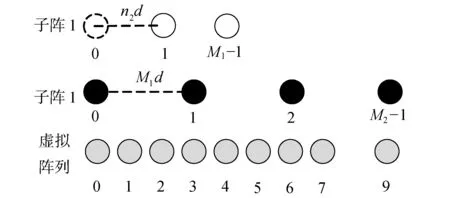
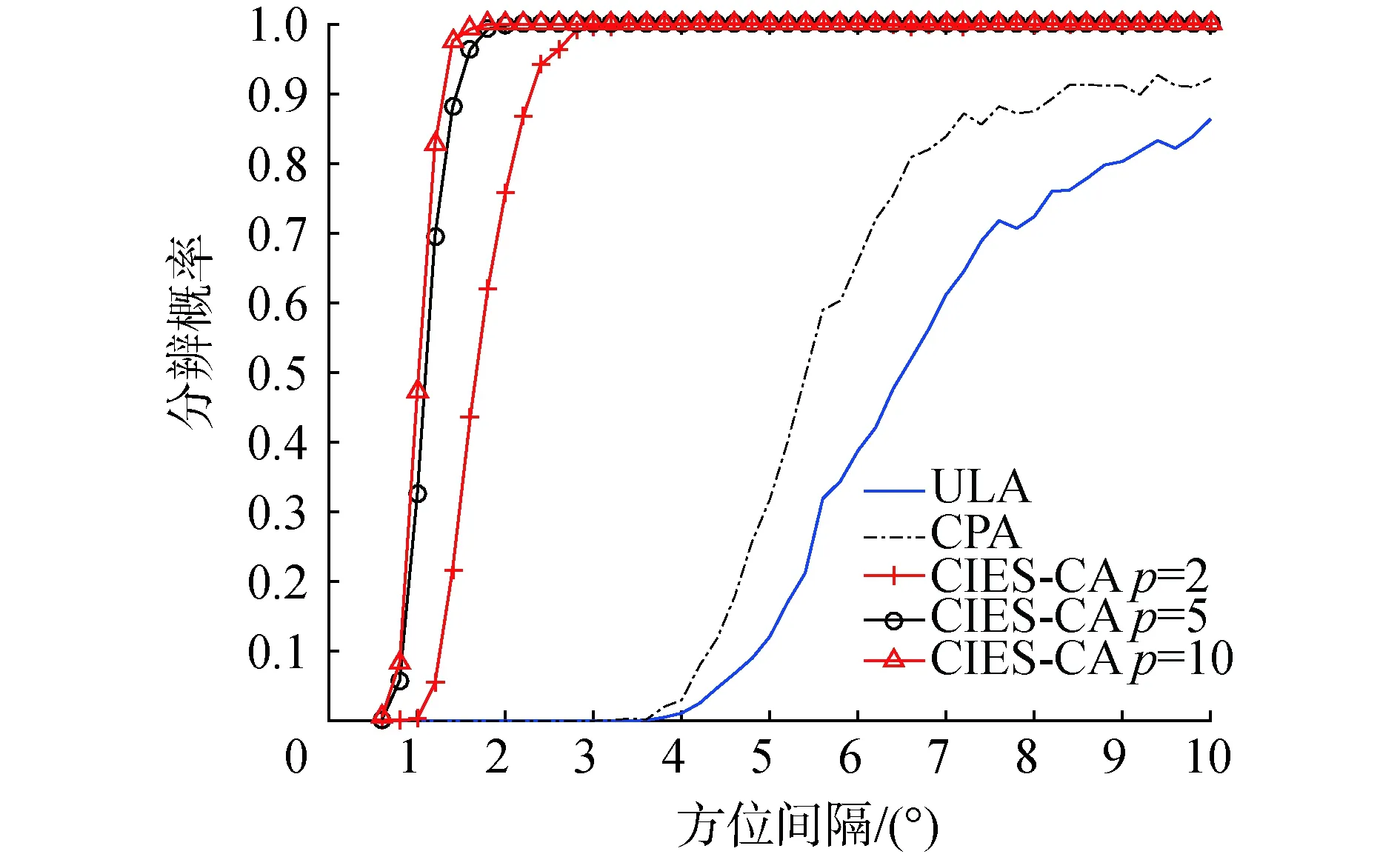
互质阵由2个子阵组成,假设子阵1含有M1个阵元,子阵2含有M2个阵元,且M1 图1 互质阵结构Fig.1 Structure of CPA 由于2个子阵共用第1参考阵元,因此互质阵总阵元数为M1+M2-1,阵列孔径表示为(M2-1)M1d。 对比相同阵列孔径的均匀直线阵列,稀疏阵列存在阵元数少,目标分辨自由度低的缺点,而虚拟阵元法能够利用稀疏阵列阵元不均匀分布的特点进行孔径扩展,从而提高信号检测的自由度和分辨率。因此,在互质阵等稀疏阵列的信号处理过程中通常会使用虚拟阵元法[7]提高自由度以适应多目标的探测情况。 以互质阵为例,各阵元的位置表示为: (1) 假设存在K个目标信号源,互质阵的阵列流形可以表示为: A=[a(θ1)a(θ2) …a(θK)] (2) (3) 式中θk表示第k个目标的来波方向。 将阵列接收信号表示为: X(t)=AS(t)+N(t) (4) 将阵列接收信号的协方差矩阵表示为: (5) 以M1=3,M2=4为例,虚拟阵列的阵元位置如图2所示。 图2 互质阵的虚拟阵元Fig.2 Virtual element of CPA 可以看到虚拟阵列中连续的阵元数为7,大于原型互质阵列的总阵元数6,提高了阵列的自由度。虚拟阵元法可以使得稀疏阵列的自由度得到一定的提高,但是由于互质阵阵型结构的原因,无法保证获得虚拟阵元全部连续,影响了虚拟阵元法阵列孔径扩展的效果。 子阵间距压缩的互质阵通过使用压缩因子改变子阵的阵元间距获得了新的阵型结构。将较大的阵元数M2表示为2个正整数p、n2的乘积,令子阵一的阵元间距由单位阵元间距的M2倍压缩为单位阵元间距的n2倍,且阵元数不变仍为M1。可以看出,此时2阵的阵元间距倍数仍然保持互质关系,且阵列孔径仍为(M2-1)M1d不变。p最小为1时阵型与原型互质阵相同,p最大为M2时转化为嵌套阵阵型。 以M1=3,M2=4为例,分别令p=2、p=4,子阵间距压缩的互质阵的结构如图3、图4所示。 图3 子阵间距压缩互质阵的虚拟阵元(p=2)Fig.3 Virtual element of CIES-CA (p=2) 图4 子阵间距压缩互质阵的虚拟阵列(p=4)Fig.4 Virtual element of CIES-CA (p=4) 可以看到p=2时虚拟阵列中连续的阵元数为8,p=4时虚拟阵列中连续的阵元数为10,均大于原型互质阵列的连续虚拟阵元数7,提高了阵列的自由度。并且,当p值越大时,虚拟阵列连续阵元数越多,自由度越高,当p值最大即等于M2时获得的虚拟阵元全部连续,自由度达到最大值。虽然在水声环境下互耦影响较小,当p值最大时阵型等同于嵌套阵,具有最好的多目标估计性能,但也具有更大的计算量。所以,在水声阵列的应用中,为了保证实时性,应当在计算量与多目标估计能力方面做出平衡。基于子阵间距压缩的互质阵列在原型互质阵与嵌套阵之间做出了平衡,可以通过p值的选择更好地适应实际需求。 多重信号分类算法(multiple signal classification, MUSIC)[8]空间谱估计是一种利用子空间分解的算法。其基本思路不同于波束形成算法的空间谱估计,突破了传统波达方向(direction of arrival, DOA)估计中瑞利限的限制,获得了超分辨的方位估计能力。基本思想是将阵列输出数据的协方差矩阵进行特征值分解,从而得到与信号分量相对应的信号子空间与信号分量相正交的噪声子空间,然后利用这2个子空间的正交性来估计信号的方向。 假设阵元数为M,目标信号源数量为K,则阵列接收信号可以表示为信号与噪声2部分,对协方差矩阵进行特征分解可以得到: (6) 式中:US表示信号子空间;UN表示噪声子空间。 对特征值向量从大到小排列,前K个较大的特征值对应信号子空间US,其余较小的特征值对应噪声子空间UN。由于信号子空间与噪声子空间正交,得到空间谱估计结果: (7) 此外,当接收信号为相干源时,需要通过空间平滑算法[9]提高方位分辨能力。 当扫描角度等于期望角度时,分母接近为0,能够形成较高的谱峰。利用角度扫描搜索可以较准确地估计空间谱的情况,获得信源的方位信息情况。 模拟多目标情况下的空间谱估计结果,模拟互质阵M1=7、M2=10,单位阵元间距为200 Hz对应半波长,分别取p=2,5,10。假设存在10个目标,在-60°~60°内均匀分布,采样率为10 kHz,采集1 s信号。利用MUSIC算法得到空间谱估计结果如图5所示。 图5 多目标空间谱估计结果Fig.5 Multi-target spatial spectrum estimation results 可以看到不同间距压缩参数下的互质阵均能有效地估计多目标方向,并且p值越大自由度越大,多目标估计能力越强。此外,当目标数目K逐渐增多时,子阵间距压缩的互质阵将按p值由小到大的顺序依次丧失对全部多目标实现方位估计的能力。 为了分析子阵压缩的互质阵的多目标方位分辨能力,模拟互质阵M1=7、M2=10,分别取p=2,5,10,同时模拟原型互质阵与均匀直线阵。假设存在2个目标,第1个目标位于50°固定不变,第2个目标从50.6°到60°变化,2目标间隔从0.6°到10°变化,经过1 000次蒙特卡洛试验,统计得到不同方位间隔下各阵型的多目标方位分辨概率结果如图6所示。 图6 不同阵型下的多目标方位分辨概率与信号源方位间隔的关系Fig.6 Relationship between azimuth resolution probability of multiple targets and azimuth interval of signal source under different formations 如图6可以发现,原型互质阵的多目标方位分辨能力要强于均匀直线阵。此外,相比于原型互质阵,子阵压缩的互质阵的多目标方位分辨能力更高,且压缩倍数越大多目标方位分辨能力越高。 分析不同阵列结构下的方位估计误差,模拟互质阵M1=7、M2=10,分别取p=2,5,10,同时模拟原型互质阵与均匀直线阵。首先分析单目标情况,假设单目标位于60°方向,信噪比从-5 dB到10 dB变化,经过1 000次蒙特卡洛试验,统计得到不同信噪比下各阵型的单目标方位估计误差结果如如图7所示。 图7 单目标方位估计误差与信噪比的关系Fig.7 Relationship between single-target bearing estimation error and signal-to-noise ratio 如图7,可以看到单目标条件下,子阵压缩的互质阵方位估计性能始终优于原型互质阵。在低信噪比的情况下原型互质阵性能弱于均匀直线阵,但随着信噪比的增加,原型互质阵性能优于均匀直线阵。 分析多目标情况,假设存在5个目标,在-60°~60°内均匀分布,其余仿真条件保持不变,蒙特卡洛仿真结果如图8所示。 图8 多目标方位估计误差与信噪比的关系Fig.8 Relationship between multi-target bearing estimation error and signal-to-noise ratio 如图8,可以看到在多目标条件下,子阵压缩的互质阵方位估计性能始终优于原型互质阵。但随着信噪比的升高,基于虚拟阵元法的各型互质阵性能均呈现变差的趋势,当信噪比升高到一定程度后性能弱于均匀直线阵。 水声阵列方位估计的过程中,除了需要面对多目标的问题外,还存在难以避免的阵列误差问题,会对方位估计以及目标方位分辨的能力产生影响。因此,在分析水声阵列的多目标方位估计能力时还需要考虑阵型在阵列误差存在的情况下,阵列对多目标方位估计的性能。本节主要针对水声中常见的多阵元通道幅相误差[10]与阵元位置误差进行分析。 阵元通道的幅相误差是一种复增益误差,通常是由于接收通道内放大器的增益不一致造成的,这一幅相误差直接影响阵列接收信号的导向向量。幅相误差可以表示为: Γ=diag{ρ1ejφ1,ρ2ejφ2,…,ρmejφm} (8) 式中:ρm为第m通道阵元的幅度误差;φm为第m通道阵元的相位误差。 假设ρm服从均值为1、均方差为0.1的高斯分布,φm服从均值为0°、均方差为10°的高斯分布,模拟互质阵M1=7、M2=10,分别取p=2,5,10,同时模拟原型互质阵与均匀直线阵。分析幅相误差存在情况下的多目标方位分辨概率与信号源方位间隔的关系。假设存在2个目标,第1个目标位于50°固定不变,第2个目标从50.6°到60°变化,2目标间隔从0.6°到10°变化,经过1 000次蒙特卡洛试验,统计得到不同方位间隔下各阵型的多目标方位分辨概率结果如图9所示。 图9 幅相误差存在情况下的多目标方位分辨概率与信号源方位间隔的关系Fig.9 Relationship between the azimuth resolution probability of multiple targets and the azimuth interval of the signal source in the presence of amplitude and phase errors 如图9可以发现,原型互质阵的多目标方位分辨能力要强于均匀直线阵,此外,相比于原型互质 阵,子阵压缩的互质阵的多目标方位分辨能力更高,且压缩倍数越大多目标方位分辨能力越高。对比图6可发现,幅相误差存在情况下,原型互质阵与均匀直线阵的多目标方位分辨概率明显下降,而子阵压缩的互质阵则性能保持较好。 具体分析子阵压缩的互质阵的多目标方位分辨概率随着幅相误差增大的变化趋势。假设第1个目标位于50°,第2个目标位于51.3°,假设只存在一种误差的基础上,分别逐渐增大幅度和相位误差的均方差,阵型参数不变,经过蒙特卡洛试验,统计得到不同误差下各阵型的多目标方位分辨概率结果如图10所示。 如图10可以发现,在不同的压缩倍数下,子阵压缩互质阵的多目标方位分辨能力均会随着幅相误差的增大而减弱,此时高压缩比的阵型分辨概率明显更强。 进一步分析幅相误差对多目标方位估计误差的影响,假设存在5个目标,在-60°~60°均匀分布,假设只存在一种误差的基础上,分别逐渐增大幅度和相位误差,保持阵型参数不变,经过蒙特卡洛试验,统计得到不同误差下各阵型的多目标方位估计误差结果如图11所示。 图10 多目标方位分辨概率与幅相误差的关系Fig.10 Relationship between azimuth resolution probability of multiple targets and amplitude and phase errors 图11 多目标方位估计误差与幅相误差的关系Fig.11 Relationship between multi-target azimuth estimation error and amplitude-phase error 如图11可以发现,在不同的压缩倍数下,子阵压缩互质阵的多目标方位估计误差均会随着幅相误差的增大而增大,此时高压缩比的阵型分辨概率明显更强。且相比于子阵压缩互质阵,均匀直线阵的估计误差明显增大,当幅相误差大于一定阈值时均匀直线阵的估计误差大于子阵压缩互质阵。 阵列导向向量是阵列对空间单位功率信源的空间响应,它与阵元的空间位置密切相关,不同的空间位置对应导向向量中不同的传播时延从而造成不同的空间响应,所以当阵元位置出现扰动时,可以等效为阵列导向向量中存在方向依赖的相位扰动。 理想阵元位置表示为: Pos=[(x1,y1),(x2,y2),…,(xM,yM)] (9) 阵元位置误差表示为: ΔPos=[(Δx1,Δy1),(Δx2,Δy2),…,(ΔxM,ΔyM)] (10) 实际阵元位置表示为: (11) 式中:Δxm、Δym为第m阵元的x、y轴坐标误差。 假设Δxm、Δym服从均值为0、均方差为0.1 m的高斯分布,模拟互质阵M1=7、M2=10,分别取p=2,5,10,同时模拟原型互质阵与均匀直线阵。分析幅相误差存在情况下的多目标方位分辨概率与信号源方位间隔的关系。假设存在2个目标,第1个目标位于50°固定不变,第2个目标从50.6°到60°变化,两目标间隔从0.6°到10°变化,经过1 000次蒙特卡洛试验,统计得到不同方位间隔下各阵型的多目标方位分辨概率结果如图12所示。 图12 阵元位置误差存在情况下的多目标方位分辨概率与信号源方位间隔的关系Fig.12 Relationship between multi-target azimuth resolution probability and signal source azimuth interval in the presence of array element position error 如图12可以发现,原型互质阵的多目标方位分辨能力要强于均匀直线阵,此外,相比于原型互质阵,子阵压缩的互质阵的多目标方位分辨能力更高,且压缩倍数越大多目标方位分辨能力越高。对比图6可发现,阵元位置误差存在情况下,原型互质阵与均匀直线阵的多目标方位分辨概率明显下降,而子阵压缩的互质阵则性能保持较好。 具体分析子阵压缩的互质阵的多目标方位分辨概率随着阵元位置误差增大的变化趋势。假设第1个目标位于50°,第2个目标位于51.3°,逐渐增大位置误差,阵型参数不变,经过蒙特卡洛试验,统计得到不同误差下各阵型的多目标方位分辨概率结果如图13所示。 如图13可以发现,在不同的压缩倍数下,子阵压缩互质阵的多目标方位分辨能力均会随着阵元位置误差的增大而减弱,此时高压缩比的阵型分辨概率明显更强。 继续分析阵元位置误差对多目标方位估计误差的影响,假设存在5个目标,在-60°~60°均匀分布,逐渐增大阵元位置误差,保持阵型参数不变,经过蒙特卡洛试验,统计得到不同阵元位置误差下各阵型的多目标方位估计误差结果如图14所示。 图14 多目标方位估计误差与阵元位置误差的关系Fig.14 Relationship between multi-target azimuth estimation error and array element position error 如图14可以发现,在不同的压缩倍数下,子阵压缩互质阵的多目标方位估计误差均会随着阵元位置误差的增大而增大,此时高压缩比的阵型分辨概率明显更强。且相比于子阵压缩互质阵,均匀直线阵的估计误差明显增大,当阵元位置误差大于一定阈值时均匀直线阵的估计误差大于子阵压缩互质阵。 1)结果表明子阵压缩的互质阵能够有效地估计多目标方向,且压缩倍数越大能估计的目标数目越多。 2)在低信噪比条件下,不同压缩倍数下子阵压缩互质阵的性能均高于均匀直线阵与原型互质阵,且压缩倍数越大多目标方位分辨能力越高、估计误差越低。 3)随着阵列误差的增大,基于子阵压缩的互质阵列受阵列误差的影响小于均匀直线阵,性能下降更慢,在抗阵列误差影响方面具有更高的的稳健性。
1.2 虚拟阵元法
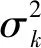
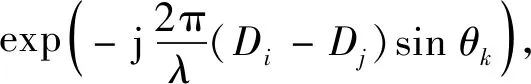
1.3 基于子阵间距压缩的互质阵列

2 水声阵列多目标方位探测性能分析
2.1 MUSIC空间谱估计
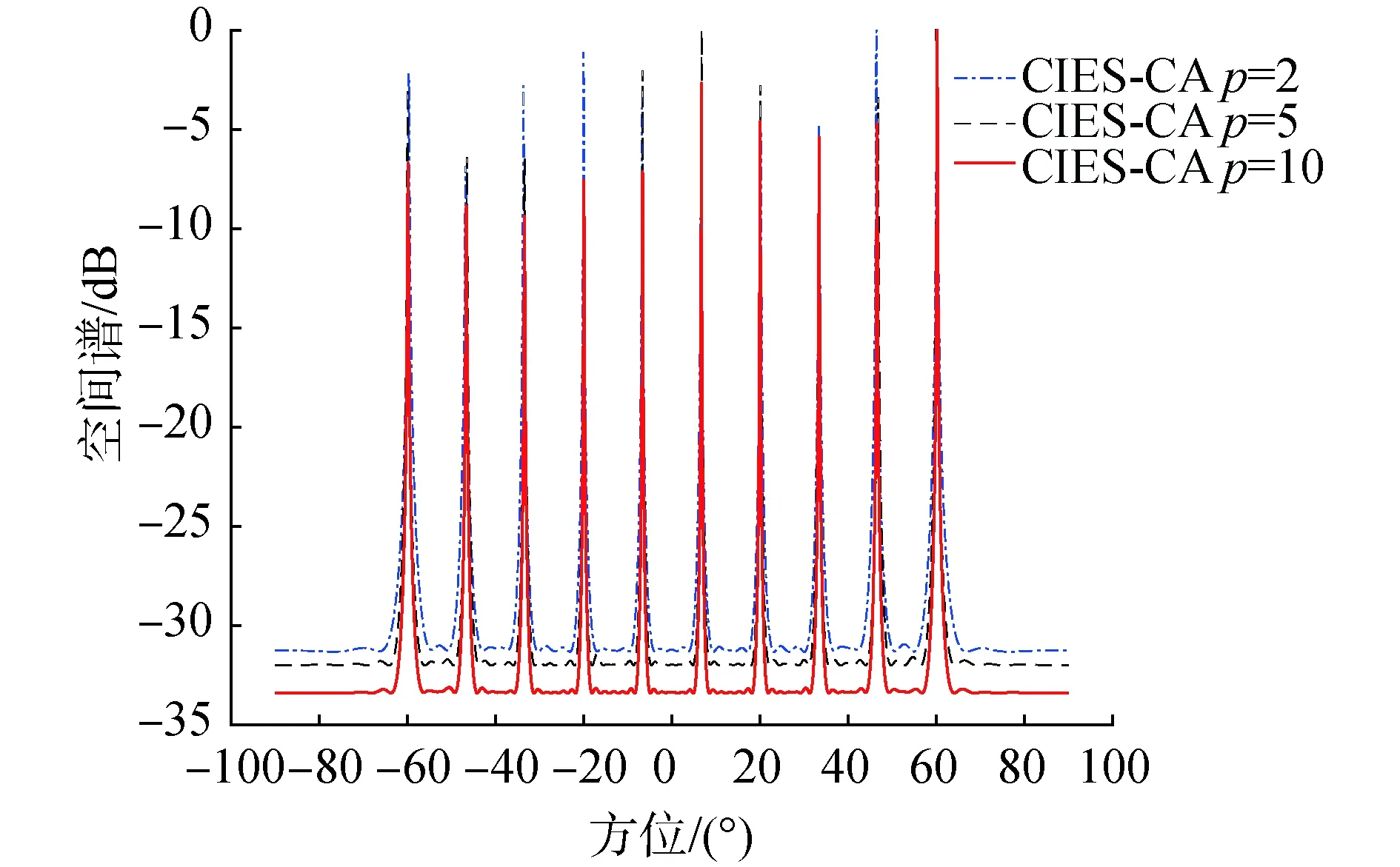
2.2 多目标估计能力

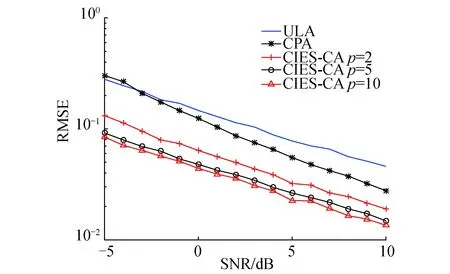
2.3 方位估计误差
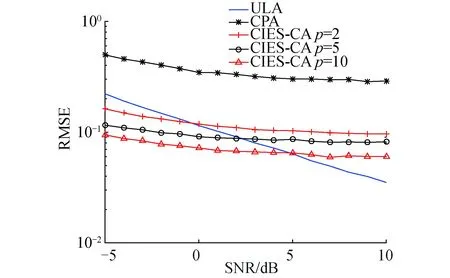
3 阵列误差对方位估计性能的影响分析
3.1 通道幅相误差条件下的多目标方位估计

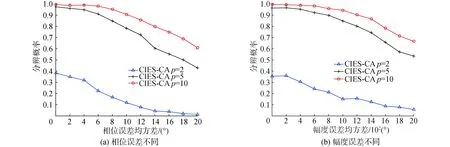

3.2 阵元位置误差条件下的多目标方位估计

4 结论

