对称轨道型单侧碰撞非线性能量阱的振动抑制

黎文科， 杨铁军， 李新辉

(哈尔滨工程大学 动力与能源工程学院，黑龙江 哈尔滨 150001)

结构在极端载荷作用下容易发生破坏，造成严重的经济损失及人员伤亡。有效控制结构振动一直是各国学者研究的热点问题[1]。非线性能量阱(nonlinear energy sink, NES)是一种新型的被动振动控制设备，当其与主结构相连接时，由于非线性作用力的原因，常常具有独特的动力学特性。例如，NES能够实现从主结构向NES单向地、不可逆地传递能量，这种现象被称为靶能量传递[2-3]。另一方面，NES还能够实现能量从低频振动向高频振动的转移，由于在相同能量水平下，高频振动常常具有幅值较小，更容易被阻尼等耗散的特点，这种能量转移能够有效的降低结构动力学响应[3-4]。轨道型非线性能量阱(track NES)是一种新型的NES，由Wang等[5]提出之后就受到学者的广泛关注。不同于其他NES设备，轨道型NES通过设置一个质量在特定的轨道上运动实现非线性回复力。数值仿真[5]和实验研究[6]都表明，轨道型NES能够有效地抑制结构在地震载荷作用下的动力学响应。进一步的，刘中坡等[7]将轨道型NES应用于大型楼房结构的抗震控制之中，实验结果表明，在多种地震载荷作用下，轨道型NES均能有效地抑制结构响应，尤其对位移均方根响应控制效果最为突出。随后，刘中坡等[8]又将轨道型NES应用于高层结构的脉动风振控制之中，结果表明，优化的轨道型NES能够同时抑制多个模态的振动，提高建筑在脉动风振载荷作用下的舒适程度。在轨道型NES设计过程中，轨道形状，NES质量以及阻尼等是重要的设计参数，不同的参数将会导致不同的控制效果。因此，对轨道型NES设计参数的研究和分析对其实际应用有着重要的指导意义。王菁菁等[9]研究发现，当实际输入系统中的能量与设计输入能量差异较大时对轨道型NES性能的影响较大，但是这种影响可以通过调节阻尼而消除。王菁菁等[10]还比较了不同轨道形状对轨道型NES性能的影响，并从控制效果和实际实现等方面给出了轨道形状的选择建议。Lu等[11]给出了一种轨道型NES的参数优化的通用方法，并将其应用于大型结构的振动控制之中，实验结果验证了优化策略的有效性。碰撞过程会导致速度的迅速改变，并伴有能量损失，在NES的设计过程中常常被考虑。Wang等[12]通过在轨道型NES的基础上增加一个单侧的碰撞表面，将其扩展成单侧碰撞轨道型非线性能量阱(single-sided vibro-impact track nonlinear energy sink, SSVI Track NES)。该SSVI Track NES在运动过程中会产生光滑和非光滑非线性回复力。并且由于碰撞表面的引入，进一步增强了能量从低频振动向高频振动的转移。大量结果表明这种SSVI Track NES能够在更宽的范围内有效抑制结构振动响应。Li等[13-14]考虑了主结构竖直方向的动力学特性，并通过数值仿真发现SSVI Track NES能够将主结构水平方向的振动转移至竖直方向的振动。对于建筑结构，由于结构竖直方向的刚度通常很大，且不容易发生破坏。因此，水平方向向竖直方向的能量转移有利于保护结构。受到以往研究[13-15]的启发，本文提出一种对称单侧碰撞轨道型非线性能量阱(symmetric single-sided vibro-impact track nonlinear energy sink, SSSVI Track NES)，克服了SSVI Track NES振动控制性能受载荷方向的影响这一问题。首先，推导系统的动力学方程，并讨论设计参数变化对其振动控制性能的影响。经过研究发现，SSSVI Track NES不仅仅是2个SSVI Track NES的简单组合，还存在更加复杂的动力学过程，会产生更复杂的运动。数值仿真表明，SSSVI Track NES不仅能够有效的抑制结构动力学响应，实现能量从低频振动向高频振动的能量转移，还对轨道形状及NES质量等设计参数的差异具有很强的鲁棒性，这对其实际应用具有十分重要的现实意义。

1 对称轨道型单侧碰撞NES

作为一种新型的NES，SSSVI Track NES不仅具有SSVI Track NESS的优点：通过与待减振结构之间的光滑和非光滑非线性回复力，实现在较短的时间内迅速降低结构动力学响应。对称布置可以克服SSVI Track NES对于外部载荷方向的敏感性这一问题。

如图1为带有SSSVI Track NES的系统示意图。主结构为1个单自由度线性振子，其质量为m1，通过刚度为k1的线性弹簧和阻尼系数为c1的线性阻尼与基础相连接，其位移用X1表示。SSSVI Track NES由2个质量mN1和mN2分别在形状H1(U1)和H2(U2)的轨道上运动构成，其中U1和U2分别代表质量mN1和mN2的相对于主结构的位移，XN1和XN2分别代表质量mN1和mN2的绝对位移。NES与主结构之间为线性阻尼，阻尼系数分别为cN1和cN2。在距离轨道底部B和-B的位置布置碰撞表面，当NES中的质量运动到碰撞表面时，NES与主结构发生碰撞，同时伴有动量交换和能量损失。

图1 对称轨道型单侧碰撞NES系统示意Fig.1 SDOF system with a SSSVI track NES

1.1 非碰撞间隔运动方程

假设SSSVI Track NES的2个质量mN1和mN2在运动过程中均不与轨道分离。当质量块mN1和主结构质量m1之间的相对位移大于间隙-B、且非线性能量阱的质量块mN2和主结构质量m1之间的相对位移小于间隙B时，NES中的2个质量均未达到碰撞表面，主结构与SSSVI Track NES不发生碰撞。此时，整个系统的势能为：

(1)

整个系统的动能为：

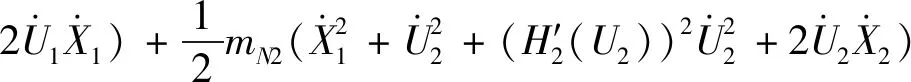
(2)

非保守力所做虚功为：

(3)

将式(1)～(3)分别代入拉格朗日方程：

(4)

可以得到系统的运动方程：

(5)

式中：U1、U2分别代表SSSVI Track NES中质量mN1和mN2相对主结构的位移；X1代表主结构位移，重力加速度为g。NES在运动过程中产生的非线性回复力为：

(6)

式中FNi(i=1,2)分别代表SSSVI Track NES中质量mN1和mN2在运动过程中产生的非线性恢复力。

(7)

其中NES在运动过程中产生的无量纲化非线性回复力为：

1.2 碰撞时运动方程

当主结构与SSSVI Track NES的相对位移之差等于碰撞间隙的时候，主结构与SSSVI Track NES质量发生碰撞。假设在碰撞的时，主结构和SSSVI Track NES的速度迅速改变，SSSVI Track NES与主结构之间发生动量的交换，同时伴有能量损失。碰撞结束后，SSSVI Track NES和主结构又以新的初值运动，直至下一次碰撞发生。假设碰撞是一瞬时发生的，恢复系数为：

(8)

式中上标-和+分别表示碰撞前时刻和碰撞之后时刻。当SSSVI Track NES中的2个质量mN1或mN2中仅有1个与主结构m1发生碰撞时，通过引入动量守恒定律，碰撞前后SSSVI Track NES和主结构的速度为：

(9)

然而，整个系统在运动过程中还存在另一种碰撞，即SSSVI Track NES的2个质量同时到达碰撞边界，则会发生3个质量的相互碰撞。结合恢复系数定义及动量守恒方程可以得到：

(10)

因此，SSSVI Track NES不仅仅是2个SSVI Track NES的简单对称布置，而是存在更加复杂的动力学行为。

2 仿真结果及分析

在仿真过程中检测SSSVI Track NES的质量mN1或mN2是否抵达碰撞表面。若判断结果为真，则中断仿真，判断此时属于何种碰撞模式，并将速度代入到式(9)或式(10)中计算碰撞后的速度。将得到的结果视作新的初始条件，重新开始计算。

2.1 轨道形状和NES质量的影响

SSSVI Track NES由于碰撞耗散的能量如图2所示，从图中可以观察到对于质量较小的情况，碰撞耗散的能量很少，这是由于质量过于小从而不能有效的从主结构吸收能量并耗散。相比较轨道形状而言，质量对碰撞耗散的能量影响更为明显。另一方面，存在最优的轨道形状参数和质量组合使碰撞损耗的能量达到最大值(约占总能量的60%)。

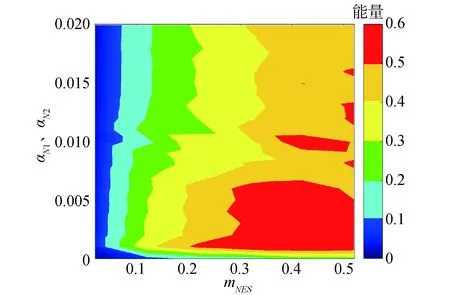
图2 碰撞耗散的能量Fig.2 Energy dissipated due to impact

从图3可以看出，随着轨道形状参数aNi的增加，阻尼耗散的能量明显降低，而说明轨道形状对阻尼耗散的能量影响较大。观察到当固定轨道形状而改变SSSVI Track NES质量参数时，阻尼耗散的能量并未发生明显改变，说明相比较NES质量而言，轨道形状对阻尼耗散的能量影响更为明显。

图3 阻尼耗散的能量Fig.3 Energy dissipated due to damping

从图4可以看出，当质量过小或者轨道形状参数过大的时候，SSSVI Track NES耗散的总能量都很少。存在1个特定的SSSVI Track NES轨道形状和质量的组合使得总耗散的能量达到最大值。

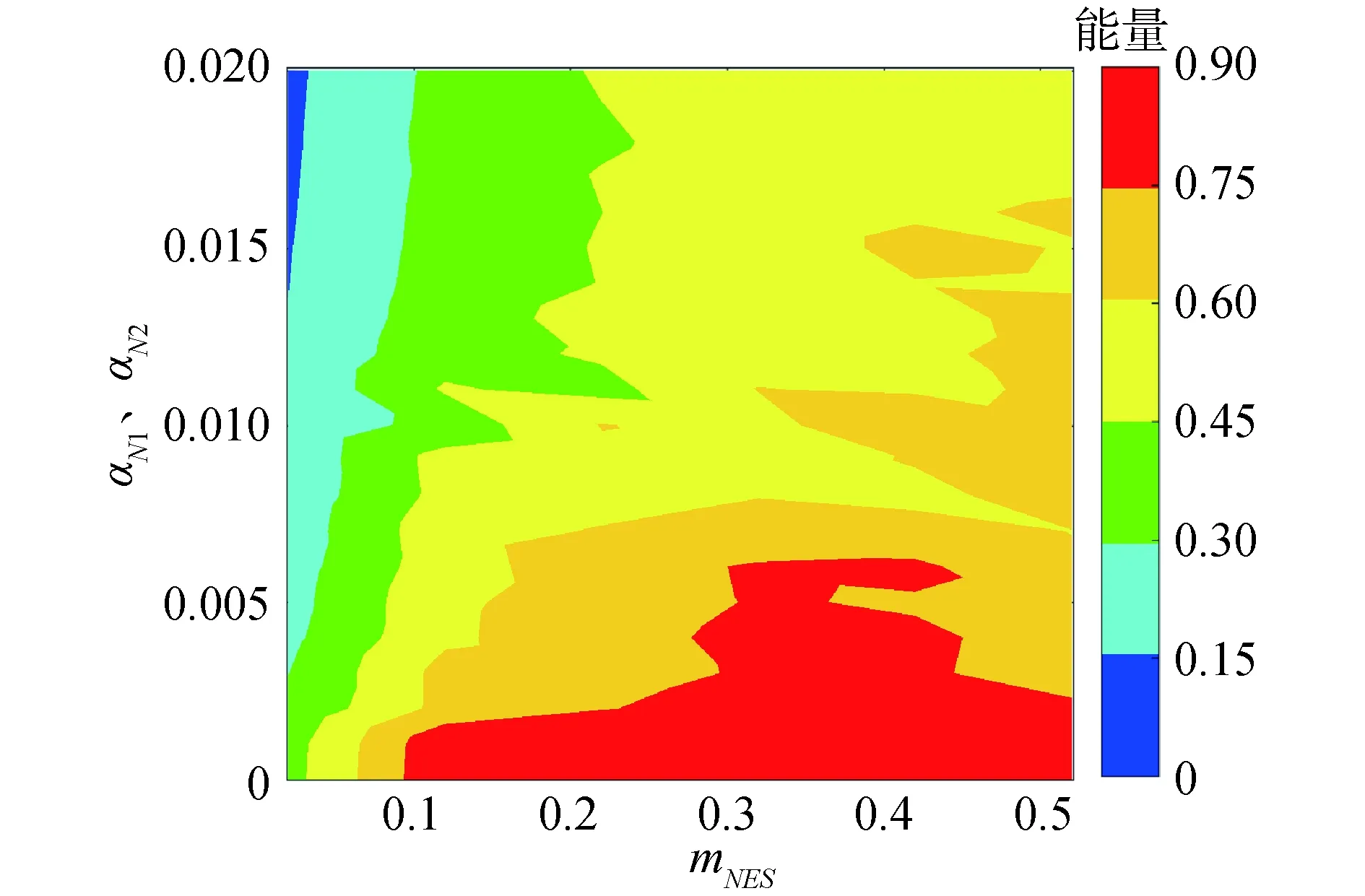
图4 总耗散的能量Fig.4 Total energy dissipated

2.2 系统响应分析

选取从图4中总耗散能量最多的NES轨道形状和质量组合aN1=aN2=0.001和mNES=0.32作为以下仿真参数。同时将SSSVI Track NES与NES锁住的情况进行对比。NES锁住是将NES与主结构固定在一起，主结构与NES之间没有相对运动，NES锁住时SSSVI Track NES的2个质量块和主结构相当于一个整体。从主结构振动的角度来看，这样选择时具有相同的附加质量。

如图5为NES锁住和NES未锁住2种情况下主结构的响应。从图5(a)可以看出，当NES未锁住时，主结构的响应迅速降低，说明SSSVI Track NES能够迅速降低结构响应。从图5(b)可以看出，除了迅速降低主结构的速度响应之外，SSSVI Track NES还会引起速度的突然改变，这种速度的突然改变是由碰撞引起的。

主结构的速度响应进行小波变换如图6所示。比较SSSVI Track NES锁住和SSSVI Track NES未锁住的情况发现，对于SSSVI Track NES锁住的情形，整个系统只存在一种频率的振动；而对于SSSVI Track NES未锁住的情形，除了低频率的振动以外，还存在更高频率的振动，说明SSSVI Track NES能够实现低频振动向高频振动转移。结合图5可知这种低频振动向高频振的转移主要是由碰撞引起的。低频振动向高频振的转移对于降低结构振动响应是有意义的：高频振动的能量更容易被阻尼等耗散，另一方面，在同等能量量级下，高频振动的幅值小于低频振动的幅值，因此能够快速、有效地抑制结构的振动响应。

2.3 鲁棒性分析

在实际应用过程中，由于加工误差等的存在，使设备参数完全符合设计要求将会导致巨大的成本。另一方面，设备在使用过程中会存在损耗，从而导致偏离设计要求。基于这些考虑，检验SSSVI Track NES参数差异对其性能的影响则显得十分重要。SSSVI Track NES的设计参数主要体现在轨道形状和质量2个方面。首先考虑当SSSVI Track NES质量为mNES=0.32时，轨道形状变化对其降低系统中能量的影响。选取aN1=0.001，而将aN2的变化范围设置为最优值的0.8～1.2。图7可以看出，随着aN2/aN1的增加，碰撞耗散的能量减少，阻尼耗散的能量增加，但总耗散的能量变化不明显，说明在小范围内改变轨道形状，对其性能的影响并不大。因此，可以说明SSSVI Track NES对轨道形状差异具有很好的鲁棒性。

图5 主结构的响应Fig.5 Primary structure response

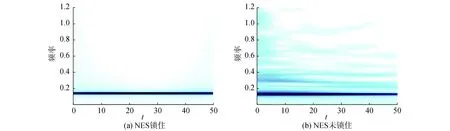
图6 主结构速度响应小波变换Fig.6 Wavelet spectrum of velocity response of the primary structure

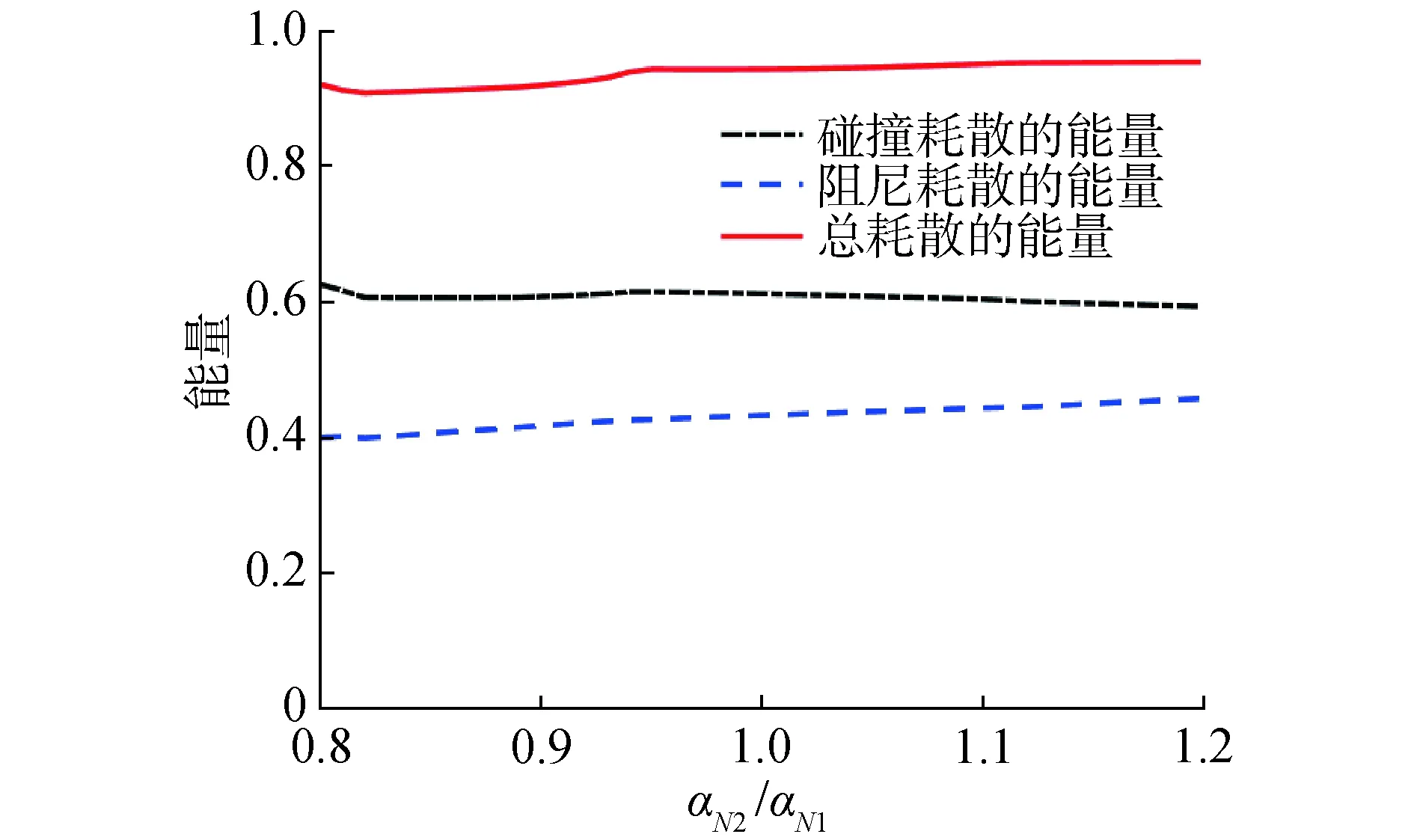
图7 对轨道差异性的鲁棒性Fig.7 Robustness to track shape differences

为了检验SSSVI Track NES中2个质量mN1和mN2之间的差异对其性能的影响，固定mN1=0.16，而将mN2的变化范围设置为最优值的0.8～1.2倍。从图8可以观察到，随着mN2/mN1的增大，总耗散的能量和碰撞耗散的能量均增加，而阻尼耗散的能量减少。注意到，碰撞的耗散能量的增加会更有利于系统响应的降低，这主要是由于碰撞会导致低频振动向高频振动转移，进而更容易将能量耗散。当mN2/mN1超过1之后，总耗散的能量增加并不明显，却导致NES的总质量增加，这是不利的，因此应该避免增加额外的质量。总体来说，SSSVI Track NES对于设计参数变化具有较强的鲁棒性。

图8 对质量差异的鲁棒性Fig.8 Robustness to mass differences

3 结论

1)本文提出一种对称单侧碰撞轨道非线性能量阱(SSSVI Track NES)，并将其应用于一个单自由度振动结构的响应控制之中。通过分析SSSVI Track NES参数变化对碰撞耗散能量、阻尼耗散能量及总耗散能量的影响，得到SSSVI Track NES的最优参数，为其设计应用提供指导。

2)优化后的SSSVI Track NES能够实现能量从低频振动向高频振动转移，并能有效降低主结构的振动响应。随着SSSVI Track NES轨道形状和质量差异的增加，整个系统中总能量的耗散并未发现明显变化，表明SSSVI Track NES对主结构振动控制性能对设计参数差异的显示了相对较好的鲁棒性和很强的实际应用价值。

本文通过数值方法研究了对称单侧碰撞轨道非线性能量阱对单自由度主结构的振动抑制性能，将对称单侧碰撞轨道非线性能量阱应用于复杂结构的振动控制及对其性能进行实验验证是后期研究的重点。