自由状态冰对螺旋桨水动力性能的影响

王超， 宋梅筠， 汪春辉， 李兴， 徐佩

(哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001)

船舶在极地航行时的工况十分复杂，常出现碎冰沿底部滑动至船艉对螺旋桨产生干扰的现象，因此在设计极区螺旋桨时，必须考虑自由运动的浮冰对螺旋桨水动力性能的影响。自由状态冰对螺旋桨水动力性能的影响分为接触干扰与非接触干扰，其中冰块的位置、进流的速度都与冰桨间的非接触干扰有关。对于冰桨间的非接触干扰，国内外学者已经开展了很多研究工作。Shih 等[1]基于2D面元法对冰阻塞工况和敞水工况下螺旋桨的水动力性能进行了计算对比，发现冰阻塞工况下螺旋桨叶元体的最大升力系数和最大阻力系数都会大幅增加，最多可至敞水工况的5.78倍；Yamaguchi[2]通过推导得出了一种改进升力面方法并进行了实践计算，认为该方法适用于冰桨非接触工况下螺旋桨的水动力性能计算；Bose[3]利用3D非定常边界元法模拟了冰阻塞流下螺旋桨的水动力性能，并将3D面元法的计算结果和Luznik等[4]的实验结果进行了对比分析，发现在冰桨非接触工况下，冰桨间距这一因素对螺旋桨水动力性能有较大影响；Veitch[5]建立了一种用于计算冰桨接触工况下螺旋桨的表面应力与冰块运动的新模型，该模型主要针对船舶大侧斜桨与水下冰块的相互作用关系这一问题；Walker[6]将冰桨干扰载荷分为接触载荷和非接触载荷，认为非接触载荷在碎冰后方的尾流场区域中会达到和接触载荷相同的量级。Liu等[7]开发了基于3-D边界元法的计算程序PROPELLA，并在此基础上添加了冰块的输入模块，与实验结果的对比证明其数值结果能较好地吻合实际情况；随后Liu等[8]对破冰螺旋桨进行了设计研究，并对3D面元法程序进行了改进，改进后该程序具备了大幅缩短螺旋桨设计过程的能力。王国亮[9]将势流理论面元法、粘流CFD技术及模型试验相结合，探讨并验证了冰的几何参数空间位置对螺旋桨水动力性能的影响规律；常欣等[10]使用重叠网格模拟了不同空间位置条件下的冰桨间非接触干扰；王超等[11]也已经开展过非接触工况下冰桨干扰水动力载荷的实验研究，建立了冰桨干扰实验台并验证了其可行性；武坤等[12]设计试验对比了均流和冰阻塞条件下的螺旋桨模型水动力性能；郭春雨等[13]以试验手段探究了固定位置的模型冰处于不同空间位置时对螺旋桨水动力性能影响的区别；李兴等[14]已经采用DFBI运动模型对冰桨非接触作用下螺旋桨对自由状态冰的运动轨迹的干扰展开了相关研究。

目前，在试验方面与数值模拟方面都已经有了不少关于冰桨间非接触干扰的研究，但其中绝大多数都在一定程度上简化了冰块的运动，仅孤立地研究固定在某个空间位置的冰块，与真实工况差别较大。因此，本文通过CFD方法模拟并分析不同进速系数下自由状态冰块对螺旋桨水动力性能的影响，对冰块的位移以及由冰块的位移带来的流场变化进行比对与分析。

1 冰浆计算模型设置

1.1 计算原理

动态流体-固体相互作用(dynamic fluid body interaction，DFBI)是指在流体中运动的过程中，对物体受到的流体动力的作用影响积分得出其运动的过程[15]。重叠网格由Steger在20世纪50年代提出的[16]，在解决不同区域的相互运动时具有明显的优势。

本文采用STAR-CCM+软件，使用DFBI与重叠网格进行相关计算。其中，自由状态冰块在水中所受合力为：

f=fr(fp+fτ+fg+∑fext)

(1)

n=fr(np+nτ+∑next)

(2)

式中：fτ和nτ为作用于物体的剪力和剪力矩；fp与np为作用于物体的力和力矩；fg为物体的重力；fr是一个阶跃函数：

(3)

式中：ts为指定释放时间；tr为释放时间。

1.2 计算模型

本文采用由R-class破冰船螺旋桨[17]改进而来的ICEPROPELLER螺旋桨[11]和中国船级社规范中强度校核推荐使用的长方体冰块模型。为了减少计算量，本文中将冰块与螺旋桨按20∶1进行了缩小。缩小后冰块尺寸为0.075 m×0.15 m×0.225 m，螺旋桨的直径D=0.2 m，主要参数如表1所示。在计算中需要先建立一个局部坐标系，原点选在冰块的质心，遵从右手坐标系，冰桨相对位置如图1所示。在释放冰块前需要对流场进行1 s的稳态计算来使流场趋于稳定，之后再释放冰块，释放过程中调用DFBI模块，并将冰块的运动设定为自由运动。

表1 ICEPROPELLER螺旋桨模型主要参数

图1 冰桨局部坐标系Fig.1 Ice-propeller local coordinate system

为了正确地模拟冰块受力状态下的运动情况，除了重力，还需要设定冰块的转动惯量矩阵。转动惯量矩阵中各个变量的定义如下:

(4)

1.3 网格划分

首先建立一个被称之为大域的圆柱体静止域，其中心位于坐标原点，直径为6倍螺旋桨直径。将大域前端设置为速度进口，后端为压力出口，前端离原点的距离为6倍螺旋桨直径，后端为10倍。同时，在坐标中心建立一个由导入的螺旋桨表面和圆柱体组成的旋转域，圆柱直径为1.5倍螺旋桨直径，前后表面以YOZ平面对称，均距离坐标轴原点0.5倍螺旋桨直径。冰块在(-0.5, 0.1,0)的位置释放。静止域、旋转域以及冰块区域如图2所示。

图2 计算域划分Fig.2 Computational domain partition graph

使用六面体网格划分大域、旋转域以及冰块域，旋转域和冰块域的外表面的边界类型设定为重叠网格。基于对冰块持续运动的计算需求，对其运动区域进行加密，冰块运动加密区为一个中心位于坐标原点、能包住螺旋桨以及冰块运动区域的圆柱体，如图3所示。

图3 截面加密Fig.3 Section diagram

此外，还要细化冰块和螺旋桨的表面网格，特别是螺旋桨的导边以及随边。冰块以及螺旋桨表面网格如图4所示。

2 计算验证与结果分析

2.1 实验流程

为了验证计算方法的正确性，本文选取1组工况在哈尔滨工程大学循环水槽进行实验，与数值模拟对比分析。

图4 螺旋桨面网格与冰块网格Fig.4 Propeller surface mesh and ice mesh

该实验选择循环水槽主要是因为循环水槽中测试模型没有前进速度而周围流场以指定速度持续运动的状况与计算模拟条件较为接近，且不受实验时间的限制，能较好地控制环境条件和实验过程，实验效率和精度较高。同时，循环水槽的宽度与深度远大于6倍螺旋桨直径，对水动力性能影响可忽略[18]。

实验中采用的装置如图5所示。根据现有研究，桨毂形状对总体水动力性能影响较小，且主要集中于叶根处[19]，对本文研究内容影响可忽略。

图5 实验设备Fig.5 Experimental equipment

实验的工况设置如下：来流速度0.6 m/s，螺旋桨转速600 r/m。进速系数计算：

(5)

式中：J为进速系数；n为螺旋桨转速；V为来流速度；D为螺旋桨直径。

由式(5)可得，本次实验的进速系数J=0.3。

实验时，正确安装实验设备，确保高速摄像机的拍摄区域能重叠地捕捉到螺旋桨及冰块运动区域，满足后期处理要求。

装置全部安装完毕后，先启动机器使水流的来流速度与螺旋桨转速达到预定值并保持稳定数秒，再通过单块碎冰释放装置释放冰块，并同时启动高速摄像机进行记录。冰块在经过实验捕捉区域后，由后方足够远处的碎冰回收装置进行回收。

在进行数据的采集和分析时使用了运动跟踪处理器(qualisys track manager，QTM)，利用2台高清摄像机捕捉被测物体上预先设置的标志物的位置，通过相关计算来求得物体的实时位置信息。

2.2 计算验证

数值模拟中，先将冰块固定0.6 s，流场趋于稳定后再释放冰块，直到冰块与螺旋桨发生碰撞，停止模拟。实验过程如图6所示。

接下来将从冰对桨的影响、桨对冰的影响2方面出发，对实验与数值模拟的数据进行对比分析。

图6 实验过程Fig.6 Experimental process diagram

如图7可见，数值模拟中在冰块距离螺旋桨较远时，推力T、扭矩Q均为较为稳定数值。冰块离螺旋桨较近时，由于冰块的阻塞使流场发生变化，T、Q均围绕平均值开始剧烈波动。

图7 推力、扭矩随时间变化曲线Fig.7 T, Q curve with time

将数值模拟与实验的结果分别代入推力系数KT和扭矩系数KQ的公式进行计算得表2，数值模拟与实验的水动力系数误差均在9%以内。

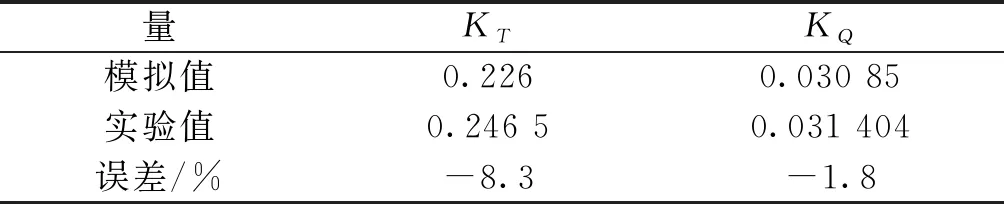
表2 数值模拟与敞水实验KT、KQ平均值

实验与数值模拟结果以冰块在x-z平面内的位移变化进行分析和对比。如图8所示。

图8 数值模拟与敞水实验的冰块位移对比Fig.8 Comparison of ice displacement between numerical simulation and open water experiment

从图8可以看出，在冰块运动轨迹方面，实验值与模拟值误差较小，变化趋势一致。在x=0.2 m左右，实验先于数值模拟发生了冰块与螺旋桨的撞击，使冰块的运动状态发生了较大改变，这一点在图中x=0.2 m处实验值的增加量突然变大可以体现出，这一现象与数值模拟结果存在一定误差，主要是由于实验中螺旋桨桨叶位置存在一定随机性，影响碰撞现象发生的时间，从总体上来看，数值模拟与真实现象的误差在可接受范围内，可以较为真实地模拟自由状态冰对流场以及螺旋桨水动力性能的影响，具有参考价值。

2.3 进速对螺旋桨水动力性能变化

本文通过式(5)确定进速与进速系数的关系，通过改变大域进口的进速V来改变进速系数J，共选取了4个进速系数(J=0.2、0.4、0.6、0.8)。

由图9可以看出，当冰块距螺旋桨较远时，螺旋桨的推力系数和扭矩系数较为稳定，而当冰块逐渐接近螺旋桨时会对螺旋桨的流场产生较大影响，水动力曲线发生明显跳跃，整体上，螺旋桨的推力系数和扭矩系数随进速系数增大而下降，且在一定的范围内进行波动，随进速系数逐渐变大，波动过程中推力系数KT逐渐高于敞水曲线，且随着进速系数变大而愈发明显。

大多数情况下，螺旋桨的推力系数低于敞水工况，扭矩系数大于敞水工况，但随着冰块在运动过程中越来越靠近螺旋桨，螺旋桨的推力与扭矩系数有可能大于敞水工况下的值。当J=0.2时，KT、KQ曲线均在冰块接近螺旋桨时表现出了遵循螺旋桨旋转周期的波动，但并未出现明显的上升或下降趋势；当J=0.4时，水动力曲线在冰块靠近螺旋桨时出现了波动上升的趋势；当J=0.6和J=0.8时，水动力曲线呈现出明显的先上升后波动的趋势。

图9 不同进速系数下的KT、KQ曲线Fig.9 KTand KQ curves with different speed coefficient

综合分析，冰块后同时存在“加速区”和“阻塞区”，当冰块离螺旋桨较远时，螺旋桨主要受其后方的加速区的影响，桨前来流整体加速，导致其推力系数和扭矩系数会下降，低于敞水工况；当冰块逐渐靠近螺旋桨，冰块的阻塞效应会明显超过其加速效应，使桨前来流速度小于敞水工况，因此推力系数和扭矩系数会变大；随着进速系数的增加，阻塞区的影响会随之增大，体现为推力系数和扭矩系数的上升趋势在数值上的增大和在时间上的提前。当冰块充分接近螺旋桨时，推力系数和扭矩系数曲线会出现显著的波动，波动周期与螺旋桨旋转周期在时间上呈现出一致性，因此可认为该震荡是加速效应与阻塞效应同时作用于螺旋桨盘面，使螺旋桨流场不均匀造成的。

综上所述，自由运动冰块对螺旋桨的影响可分为阻塞效应、加速效应，以及某些时刻由于加速效应与阻塞效应同时作用于螺旋桨盘面导致的流场不均匀造成的影响。

2.4 螺旋桨水动力性能波动情况

由图9可得，绝大多数情况下螺旋桨的推力系数会明显低于敞水工况。从数值上来分析，分别提取出各个进速系数下螺旋桨的推力系数的最大和最小值，将其差值与最大值的比值看作是推力系数的波动百分比，如表3所示。可以看出，低进速下螺旋桨的推力系数波动比较小，随着进速系数增加，推力系数波动比会逐渐增大，这是因为在高进速下，冰块后方存在一定的涡脱落现象，且这种脱落在高进速下比较明显，这使流场变化较大，最终导致螺旋桨的推力系数变化较大。此外，在高进速工况下有冰干扰的螺旋桨推力系数会超过敞水工况，因此在螺旋桨阻塞效应明显的情况下，提高进速系数会使得螺旋桨的推力系数有所提高。

表3 KT波动比Table 3 KT fluctuation ratio

2.5 某时刻不同进速下冰桨之间流场

图10是时间t=1.4 s时不同进速下冰桨相互作用下的流场图，从图中可以看出，随着进速系数的增加，冰块与螺旋桨的距离会越来越近，这是由于当进速系数增加时，流体对冰块的作用力也会随之增加，因此在t相同时冰块的运动距离会远。

图10 t=1.4 s时不同进速下流场Fig.10 Flow field diagrams at different velocities at t=1.4 s

影响冰块运动姿态的主要因素为水流的冲击作用与螺旋桨的抽吸作用，由于冰块与螺旋桨的位置关系，在Z方向上，螺旋桨的抽吸作用对冰块有一个前后不均匀的力，而水流的冲击作用在冰块发生偏转时会产生将冰块的姿态纠正回水平的力。因此当进速系数较小时，水流影响较弱，冰块姿态主要受螺旋桨的抽吸作用影响，冰块会发生一定的翻转现象；而当进速系数较大时，水流对冰块的冲击作用较大，且冰块运动较快，螺旋桨对冰块的影响时间相对较短，冰块的运动姿态变化不明显。

2.6 冰块位移变化曲线分析

图11是变进速情况下，冰块在XYZ3个方向上的位移曲线。当进速系数变大时，冰块在各个方向上的位移都随之增加，这主要是由于当进速增加时，水流对冰块的冲击作用较大，所以在X方向上的位移会增加；当进速增加时，螺旋桨旋转时会导致冰块左右和上下的压差不均匀变大，因此会导致Y、Z方向的位移增加。

图11 不同进速冰块位移曲线Fig.11 Displacement Curves of Ice Blocks with Different Forward Velocities

从上述的位移曲线可以看出，冰块位移以X轴向为主，Y、Z方向位移较小，这说明冰块主要受到水流沿X方向的冲击和螺旋桨的抽吸作用，这是在X方向产生位移的主要原因；冰块在Y方向上主要受到重力和浮力，这也是在Y方向上产生位移的主要原因，从图11中可以看出，冰块在Y方向上的位移不大，所以冰块在垂直方向上的上升并不大；冰块在运动过程中所受的侧向力很小，这也说明了在均匀来流下，螺旋桨对前方的水流不会有太大的影响，主要会对后方水流产生预旋作用。

3 结论

1)经与实验值对比，本文数值计算方法可以较好地预报非接触条件下冰桨干扰水动力性能和冰的运动轨迹。

2)自由运动的冰块后方存在一定的“加速区”和“阻塞区”，当这2种区域同时作用于螺旋桨桨盘时，螺旋桨的来流有较大的不均匀性，螺旋桨水动力系数出现周期性震荡。

3)当冰块较远时，螺旋桨受加速区影响较大，此时螺旋桨推力系数和扭矩系数会下降，低于敞水工况；当冰块逐渐靠近螺旋桨，螺旋桨受阻塞区影响较明显，此时推力系数和扭矩系数会上升。

4)随着进速系数的逐渐增加，总体上螺旋桨的推力系数和扭矩系数都会下降，阻塞区的影响会更为显著，推力系数和扭矩系数的上升趋势更显著，上升时间更长。

运动的冰块对螺旋桨的水动力性能的影响是周期间歇性的，这在螺旋桨旋转过程中会使推力和扭矩发生幅度较大的波动，可以预见，当螺旋桨转速继续提高时，螺旋桨水动力性能将呈现更大的波动性，对船体尾部区域的振动影响会更加明显，这是在螺旋桨设计过程中需要重点考虑的问题。与现有的研究相比，本文对冰桨非接触干扰的研究考虑到了冰在自由状态下，受螺旋桨与水流影响的位移，更能反映真实状态。但是，本文采取的变量主要为进速系数，后续可针对其余变量以及螺旋桨、冰块本身的变化进行测试分析。