连续摆动吊舱推进器水动力性能数值模拟
胡健, 赵旺, 王子斌, 王雅楠, 张维鹏
(哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001)
吊舱推进器是一种新型的电力推进形式,它集螺旋桨和操舵装置于一体,使得船舶具有更好的操纵性能,吊舱推进器应用于船舶推进器领域,吊舱推进器在斜流中,所受水动力载荷会发生显著变化,尤其在瞬时回转工况下,水动力载荷变化更加剧烈,需要密切关注。
关于吊舱推进器的水动力性能研究,理论方法包括基于势流理论的升力面法和面元法,Bal[1]分析了吊舱单元周围的流动情况,并对螺旋桨在吊舱上的性能特性进行了研究。杨晨俊等[2]采用单桨吊舱推进器的定常计算方法,计算了吊舱与桨叶之间的相互影响。胡健等[3]用迭代方法求解了吊舱和螺旋桨之间的相互影响,并且还研究了在船后伴流中推进器的水动力性能。Liu等[4]采用面元法预测了不同方位角下吊舱推进器的非定常力、扭矩和弯矩。
国内外很多学者用CFD法做了很多工作,CFD 方法的基本思想是:用一系列连续的多面体网格分割原来连续的计算域,用网格点的变量值表示原来位置的物理量,再运用物理场中的控制方程,通过不断迭代求解得到数值解,作为物理变量的近似解[5]。Shamsi等[6]基于雷诺平均Navier-Stokes(reynolds averaged Navier-Stokes,RANS)的求解器研究了不同角度下的吊舱推进器的水动力特性的变化。王智展等[7]结合RANS法计算了吊舱桨的瞬时推力系数和扭矩系数,并计算了吊舱单元水动力系数随回转角的变化。罗晓园[8]采用面元法计算了3种不同纵斜螺旋桨的敞水特性,并结合CFD计算了不同静水系数下吊舱推进器的水动力性能。常欣等[16]研究了斜流中螺旋桨的非定常水动力性能,结果表明,斜流角度越大,单桨叶受力的脉动幅度越大。徐嘉启[17]等研究了HCRSP推进器在操舵工况的空泡性能,通过吊舱后桨与前桨的组合用以展示空泡特征。张维鹏等[18]等对斜流工况中桨舵的干扰过程进行了分析,结果表明舵表面的脉动压力受斜流和尾涡的双重影响。孙聪等[19]基于分离涡模拟方法研究了导管桨在斜流中的水动力性能,结果表明斜向来流使得桨叶水动力载荷非定常性增强。Dubbioso等[20]基于雷诺时均方程研究了10°~30°斜流角下螺旋桨的水动力性能,研究结果表明桨的推力随斜流角的增大而增大。Li等[21]对泵喷推进器的尾涡进行了比较研究,结果表明,混合RANS/LES方法能够捕捉到丰富的湍流特征。
很多学者从试验角度研究了吊舱推进器的水动力性能。Maciej[9]采用试验方法对吊舱推进器在-45°~45°的斜流角下的水动力性能开展了研究,并测量了不同进速系数下的水动力特性。Islam[10]将数值预报方法与实验评价相结合,用于探索吊舱推进器的水动力性能。赵大刚等[11]通过试验研究了L型吊舱推进器在动态操舵时的螺旋桨载荷,研究表明:右旋桨L型吊舱推进器在向右操舵时螺旋桨整体上的推力要较静态操舵状态的大。沈兴荣等[12]通过模型试验研究了拖式吊舱推进器±30°舵角时的水动力性能,分析了舵角和进速系数对吊舱推进器水动力性能的影响。张志荣等[13]应用数值方法计算了直航条件下推式和拉式吊舱推进器的水动力性能,还给出了斜航条件下吊舱推进器的流场模拟,并将其推力、扭矩等与试验值作对比。谢清程等[14]测量了0°~180°方位角下吊舱推进器的水动力特性,探索了吊舱推进装置研制中可能遇到的技术难点。
上述研究的重点主要是在稳定斜流工况下吊舱推进器的水动力性能。吊舱推进器的主要贡献之一是提高了船舶的操纵性。因此,有必要对全方位吊舱推进器的瞬态水动力载荷进行更详细的分析。本文使用数值模拟软体STAR-CCM+,进行数值模拟。在数值模拟广泛收敛性研究的基础上,分析了吊舱推进器产生的力和力矩。同时,还研究了螺旋桨载荷与水流入射角的关系。
1 吊舱推进器模型及计算域
1.1 控制方程
在选择物理模型时,假设流体恒密度不可压缩,忽略质量力,采用时间平均法建立了雷诺湍流平均方程。
连续性方程为:
(1)
动量方程为:
(2)
本文计算选用的模型为SSTk-ω湍流模型,它考虑了湍流剪应力的输运特性,能够准确预报由于逆压梯度导致的流动分离点和分离区域。SSTk-ω湍流模型方程:
k的运输方程:
(3)
ω的运输方程:
(4)
式中:u为速度;x为坐标轴(i,j=1,2,3分别表示x、y、z3个空间坐标);k为湍流动能;ω为比耗散率。F1、β、γ、σk、σω均为模型参数;β*为模型常数,取0.09。
在式(3)和式(4)中,雷诺应力的涡粘性模型为:
τtij=2μt(Sij-SnnSij/3)-2ρkSij/3
(5)
式中:μt=ρk/ω为涡粘性;Sij为平均速度应变率张量;Snn为克罗内克算子。生成项Pω为:
Pω=2γρ(Sij-ωSnnSij/3)Sij
(6)
1.2 几何模型
吊舱推进器包括螺旋桨、支架和吊舱,计算时所用的螺旋桨为四叶定距桨,旋向为右旋,相关参数如表1所示,图1给出了吊舱推进器吊舱和支架的尺寸参数。

表1 螺旋桨主要参数Table 1 Main parameters of propeller

图1 吊舱和支架的几何参数Fig.1 Geometric parameters of pod and support
1.3 计算域划分
所设置的计算域能够模拟吊舱推进器所处的工作环境,计算域应尽量设置足够大,可以避免边界水波反射对尾波系造成影响,速度进口和压力出口应与吊舱推进器保持一定的距离,这样能够得到均匀的入射流和桨后发育完全的流场。
设吊舱螺旋桨的直径为D,以下用螺旋桨直径作为度量长度的单位,用长方体代替吊舱推进器工作的水域,入口距吊舱单元的距离为3D,出口距吊舱单元的距离为6D,考虑到吊舱单元瞬时回转工况回转的工况,因此水域侧向长度设为8D,设有2个圆柱形旋转域,螺旋桨旋转域直径为1.12D,吊舱单元旋转域直径为2.4D。图2展示的是大域和近场域的位置,定义螺旋桨初始位置的轴向与x轴重合,y轴和z轴的方向如图2所示。

图2 计算域Fig.2 Computational domain
1.4 网格划分
在湍流模型下,棱柱层的设置至关重要,对于螺旋桨而言,y+值应取小于1的值,y+值过大会导致棱柱层过厚,计算结果不准确,通过经验公式可以求得第1层棱柱层的厚度[15]:
(7)
式中:L以螺旋桨直径D作为特征长度(L=0.25 m);一般来说,雷诺数Rn越大,棱柱层厚度越小,此工况下雷诺数为Rn=UrefLref/ν=8.68×105,Lref=D/2=0.125 m,Uref为螺旋桨梢端的线速度,Uref=nπD≈7.85 m/s。除了在吊舱表面设置棱柱层外,为了精细网格,还特别对吊舱特征线及其包裹的特征面进行了加密,生成的网格如图3所示。

图3 吊舱推进器表面的网格Fig.3 Mesh of podded propulsor surface
2 网格和时间步验证
从船艉向船艏看,吊舱推进器向左舷偏转为正,向右舷偏转为负。示意图如图4所示。

图4 吊舱推进器受力示意Fig.4 Force sketch of podded propulsor
螺旋桨的推力和转矩可用无因次化系数来表示,对于螺旋桨的吊舱单元的推力系数和转矩系数,分别为:
(8)
式中:n为螺旋桨的转速;i=x,y,z分别代表x向、y向和z向;Ti和Qpi分别为吊舱桨i向的受力和力矩;Fi和QU分别为吊舱单元i向的受力和转舵力矩;KTPi和KQPi代表吊舱桨i向的推力系数和力矩系数;KTUi和KQU代表吊舱单元i向的推力系数和转舵力矩系数。吊舱单元包括螺旋桨、吊舱和支架3部分。
在模拟中,通过改变来流速度来实现进速系数的变化,进速系数定义为J=VA/nD,VA代表来流速度。螺旋桨转速为n=10 r/s,吊舱单元旋转域运动的角速度函数为:
(9)
即吊舱单元的在-50°~+50°运动,运动周期为T=20/3 s,吊舱单元所处的初始位置为0°。
由于缺少高斜流角下的实验数据,因此本研究通过将用不同网格数量和时间步条件下的计算结果作收敛性验证。
2.1 网格验证
针对吊舱单元设置3组不同的网格数量,计算域内的其他网格尺寸按照同等百分比去变化,在整体网格数量发生变化时,保证y+值和时间步不变。通常在不同的网格数量下,计算得到的值之间的误差应在5%以下,特别的,对于3种及以上的情况,求解的不确定度应满足Gi+2-Gi+1≤Gi+1-Gi,即随着网格数量增加,所求的解应有逐渐稳定的趋势。表2中展示了稳定斜流工况中3种网格数量下所求解(J=0.2,θ=0°),可以看到,在Coarse Grid下,所求解与Medium Grid和Fine Grid下的结果相差较大,Medium Grid和Fine Grid下的结果相差不大,综合求解精确度和求解速度来考虑,最后网格条件选用Medium Grid。
2.2 时间步收敛性分析
时间步的选择对计算结果的收敛与否至关重要,验证过程中保证网格条件不变(Medium Grid),根据螺旋桨的转速选取了3个时间步长,分别对应每一时间步螺旋桨旋转了1°、2.5°和5°,分别对应Δt=2.778×10-4,Δt=6.944×10-4,Δt=1.388 9×10-3,以在瞬时回转工况下螺旋桨的y向力矩系数曲线为例,如图5所示。

表2 网格独立性分析Table 2 Mesh independency
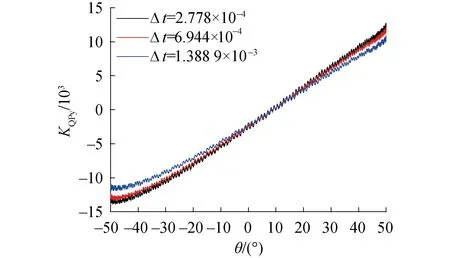
图5 不同时间步长下螺旋桨y向力矩系数Fig.5 y direction moment coefficient of propeller at different time steps
选取图5中低斜流角(-2.5°~2.5°)和高斜流角(40°~45°)2种情况观察。
在转向角为-2.5°~2.5°的过程,在图6中可以看到3条曲线几乎重合;再选取40°和45°过程,可以看到Δt=1.388 9×10-3的曲线与其他2条曲线相差较大,另外2个时间步所绘曲线虽不完全重合,但误差在5%以下,考虑到是在±50°这种极端工况下,这样的误差是可以接受的。兼顾运算速度以及计算精确度,最终选取的时间步长为Δt=6.944×10-4。
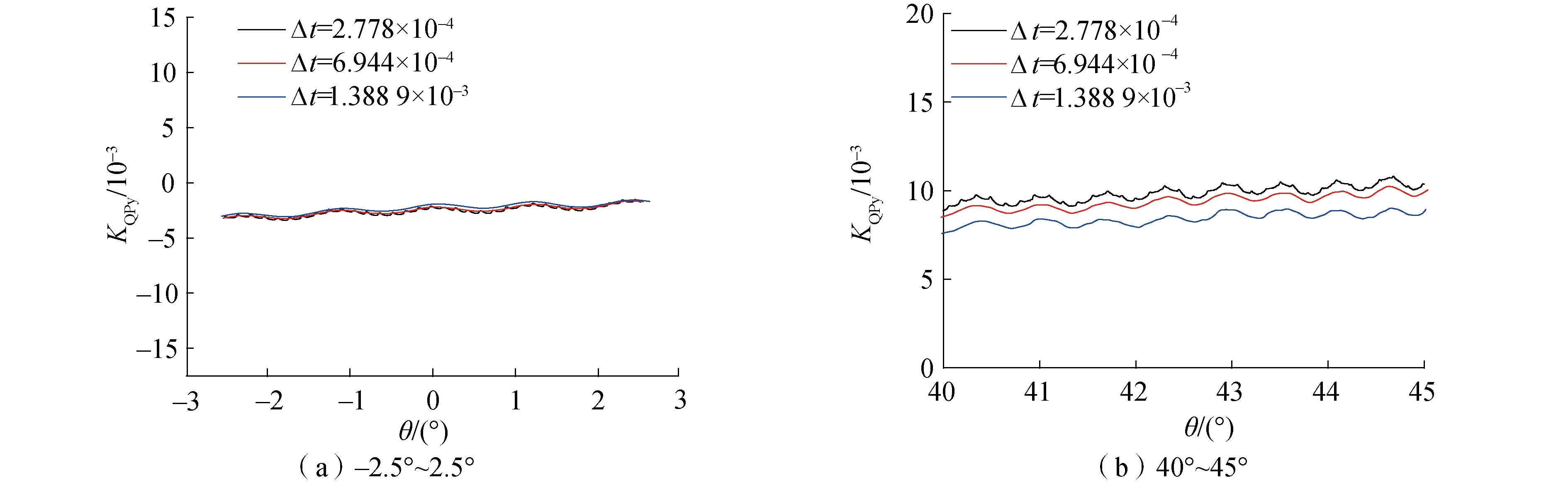
图6 2种斜流角条件下的螺旋桨y向力矩系数Fig.6 y direction moment coefficient of propeller under the condition of two oblique flow angles
3 操纵工况载荷计算
3.1 进速系数对吊舱性能的影响
图7展示了螺旋桨载荷随着进速系数的变化情况。在图7中可以看到KTPx自中间向两边逐渐增大,这是因为随着斜流角的增大,经过螺旋桨轴向的水流速度越小,进而使得螺旋桨推力增加;还可以发现在同一斜流角度下,随着进速系数增加,KTPx在减小,这是由于水流速度增加,使得经过螺旋桨轴向的水流速度变大,因此导致KTPx降低。

图7 螺旋桨x向推力系数Fig.7 x direction thrust coefficient of propeller
3.2 斜流工况
图8为斜流工况中的单桨叶受力,选取的是单桨叶0°~360° 1个周期内的载荷变化。从图8中可以看到,KTx曲线有1个波峰和1个波谷,并且随着斜流角度的增加,KTx曲线变化更为剧烈。图8中的进速系数选取为J=0.2,斜流角选取5个角度,分别为10°、20°、30°、40°和50°。
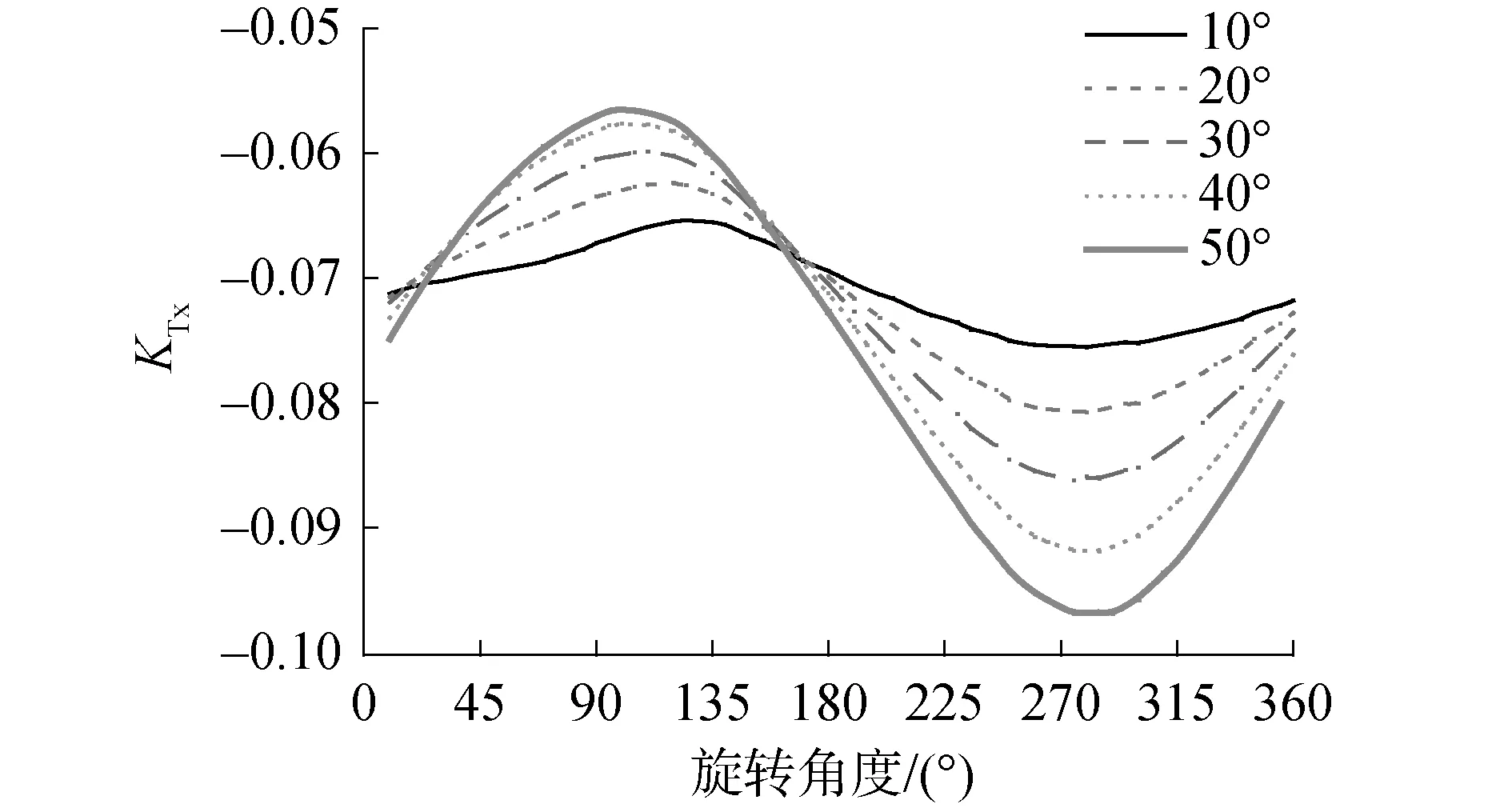
图8 单桨叶x向推力系数Fig.8 x direction thrust coefficient of single propeller blade
图9展示了吊舱单元在瞬时回转工况和斜流工况两种情况下的载荷比较,进速系数选取为J=0.2,选取了吊舱单元1个完整的运动周期从图9(a)可以看到,在斜流角为-40°~-50°时的曲线规律性不明显,这是因为吊舱单元在-50°斜流角处转向导致流场紊乱,从而使得此处力的变化更加剧烈。从图9(b)、(c)中可以看到,吊舱单元在向左转和向右转的过程中载荷并不完全重合,这说明2个过程还是有区别的。对于斜流工况的吊舱单元载荷而言,可以发现,载荷曲线与瞬时回转工况下的载荷曲线变化趋势一致,且位于其中间。

图9 瞬时回转工况和斜流工况中吊舱单元载荷对比Fig.9 Comparisons of pod unit loads under maneuvering and oblique flow conditions
图10展示的是在z=0截面处的桨后速度场,分别是在斜流角为-30°和30°下瞬时回转工况和稳定斜流工况的对比,瞬时回转工况选取的是从左舷转向右舷的过程,可以看到2种工况下的速度场存在明显差别,这是由于瞬时回转工况下的吊舱单元一直在作回转运动,导致了不定常入射流的产生。

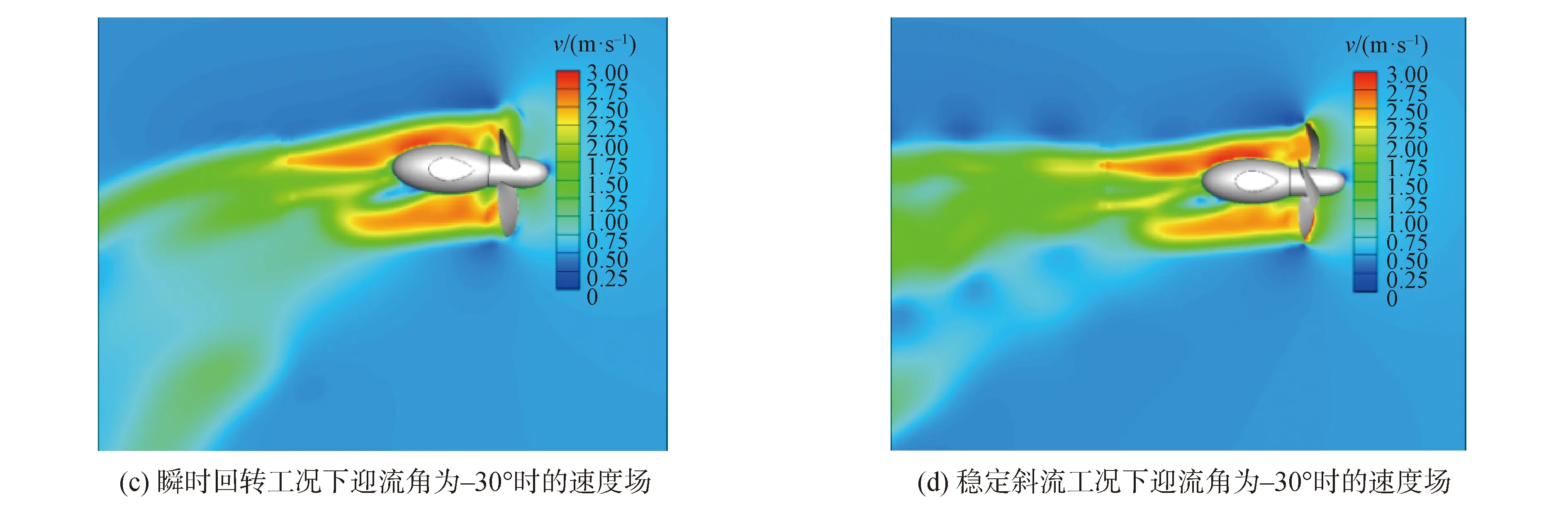
图10 在z=0截面上吊舱单元在瞬时回转工况和稳定斜流工况的速度场对比Fig.10 Comparison of velocity field of pod unit in instantaneous rotary condition and steady oblique flow conditions at z=0
4 结论
1)在稳定斜流工况下,螺旋桨x向载荷随斜流角增加而增加,y向载荷随斜流角增加而增加。
2)在瞬时回转工况下,吊舱单元在向左和向右回转2种状态下的螺旋桨载荷不同,以y向推力系数为例,在0°斜流角时,向左转时其值为-0.01,向右转时其值为-0.04。
3)在稳定斜流工况和瞬时回转工况下并不相同,以z向的推力系数为例,在0°斜流角时,稳态载荷为0.035,而吊舱单元在向左转时载荷为0.03,向右转时为0.044。

