高寒高海拔地区长大隧道温度场测试与二衬结构应力场耦合分析

陈华鑫， 黄庆庆， 何 锐， 薛 成， 白永厚

(1. 长安大学 材料科学与工程学院， 陕西 西安 710061;2. 西安市市政设施管理中心， 陕西 西安 710016;3. 中交第二公路工程局有限公司， 陕西 西安 710065)

随着我国交通基础设施快速发展，其建设重心正向西部地区转移，其中高海拔隧道越来越多，然而复杂的气候环境导致了一系列病害，例如，隧道的冻胀开裂、衬砌混凝土剥落、挂冰泛水等.国内外学者通过现场实测隧道温度场变化规律，利用有限元软件模拟隧道受力及变形，对寒区隧道温度场展开了研究.李彬嘉等[1]、C. COMINI等[2]通过完善相变热传导温度场的数值求解方法，建立了隧道有限元模型，研究了冰-水相变对寒区隧道动态温度场的影响.JUN K. J.等[3]、ZENG Y. H.等[4]采用变量控制法，通过控制风速、风温、时间、距离及有无保温层，探究了隧道洞内及围岩的温度变化规律.南方地区隧道多富水，温度场的研究必须考虑渗流场的耦合非线性问题，隧道的主要病害集中在渗漏水.北方寒区隧道冻胀问题显著，很多学者通过建立寒区隧道温度场计算模型，对冻结的深度和隧道保温层的厚度进行研究.在西部高海拔地区，由于特殊的地理环境，导致年温差和昼夜温差较大，加之隧道二衬结构属于超静定结构，温差作用使二衬内部产生温度应力，尤其造成隧道洞口段二衬结构开裂明显[5-7].现有研究多关注平原地区隧道温度场模型的建立，且所依托的隧道大多数属于短小隧道，而对于高寒高海拔地区长大隧道温度场与二衬结构应力场研究相对较少.

为此，以西藏地区某长大隧道为依托，选取典型断面展开温度场研究，运用有限元软件，结合现场实测温度场数据对隧道二衬结构进行模拟，探讨大温差环境下隧道二衬结构的变形，以及应力分布特点，量化二衬结构出现破坏时的温度应力占比，以期为高海拔大温差环境下隧道建设提供理论依据和参考.

1 隧道温度场测试内容

1.1 工程概况

隧道位于西藏自治区，隧址区海拔4 400 m.隧址区内气候干燥、缺氧、温差大、日照充足，根据达孜气象站2018年全年观测数据资料，月极端最高气温27 ℃，月极端最低气温-15 ℃，全年最大温差42 ℃.隧道系左右分离式双洞隧道，两洞相距20.0～37.0 m，隧道全长12.8 km，未贯通.进口浅埋5.5 m，单洞开挖断面面积81.4 m2.主洞洞身围岩级别：III级占30%，IV级占60%，V级占10%.

1.2 测试项目与设备

测试仪器包括温度计(-50～50 ℃)、YTTYJ20A型振弦式土压力盒、测温探头、数显仪等.YTTYJ20A型振弦式土压力盒量程为2.00 MPa，灵敏度为0.01 MPa.

1.3 测试断面布置

隧道中选取9个测试断面.由于隧道洞口段温度场的变化较洞内更为复杂，洞内纵深温度场趋于稳定，因此洞口段测点较密集，洞内逐渐增大测试间距，分别在洞外50 m及洞内5、20、50、100、300、500、1 000和1 600 m处布设测温计，编号依次为①、②、…、⑨.

在②、⑥、⑦和⑧断面进行隧道围岩温度的监测，隧道初期支护完工后，立即打孔埋设.测温探头布置在隧道截面的拱顶、边墙和拱腰部位，探头每隔0.6 m设置一个，延伸至围岩深度3.0 m处，每个断面设置25个测温探头.

在②、⑧断面对二衬结构的接触压力进行监测，每个断面布设5个监测点，在二次衬砌浇筑之前，由拱顶开始每隔30°布置一个测试元件.

压力盒数据通过频率读数仪进行采集并保存，可通过USB接口导入到电脑中进行处理.接触压力计算公式为

F=K(f2-f02)，

(1)

式中：F为接触压力，MPa；K为测试元件标定系数，MPa·Hz-2；f为实测频率，Hz；f0为仪器测得初始频率，Hz.

2 隧道温度场分布规律

2.1 隧址区全年空气温度变化规律

图1、2分别为该隧道所在地2018年全年的日均气温与日温差变化规律曲线.

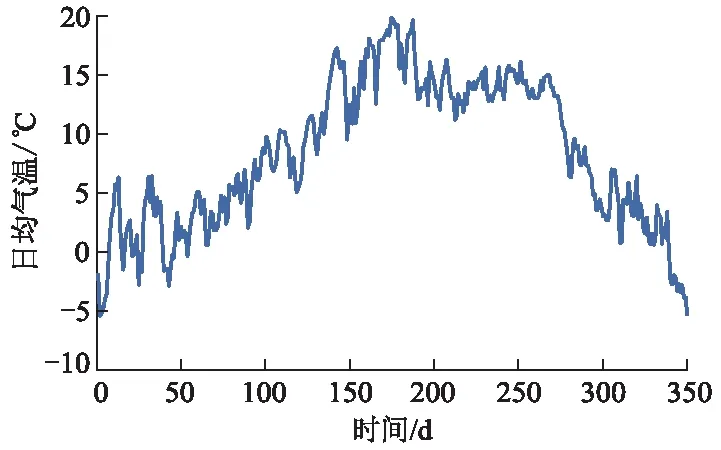
图1 全年日均气温变化规律

由图1可知：温度变化趋势为正弦曲线，温度曲线随着测试天数的增加呈先上升后下降的趋势；最高日均温度为6～7月，最低为1～2月.隧址区全年日均最高气温达到20.0 ℃，最低气温为-5.5 ℃，全年最大日均温差约为25.0 ℃.

由图2可知：隧址区最小日温差4.7 ℃，最大日温差为25.3 ℃；最大温差出现在1～2月，最小温差出现在7～8月.分析认为：隧道位于海拔4 400 m处高原地带，云层稀薄，1～2月温度下降明显，白天接受太阳照射强度较大，地面升温较快，因此温差比较大；在7～8月，整体气温较高，夜晚温度散失较少，因此温差较小.为了探究大温差环境对于隧道内温度场及二衬结构的影响，结合该地区温差变化规律，试验选择在温差最大的1～2月进行.

图2 全年日温差变化规律

2.2 隧道内温度变化规律

在隧道洞口、⑥、⑦、⑧号断面布设测温计，进行实时监测洞内各断面24 h的温度变化.初测时间为凌晨5点，24 h后得到不同断面温度变化规律曲线如图3所示.

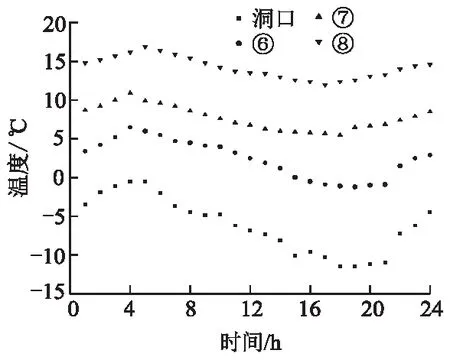
图3 各断面24 h空气温度变化规律

图3可知：隧道各断面温度变化曲线接近正弦函数，随着入洞深度的增加，温度变化幅度逐渐减小，洞口最大温差为11.0 ℃，⑧号断面最大温差为4.9 ℃.平原地区温度峰值出现在下午2点左右，温度最低值出现在上午7点左右.在高原地区实测一天中温度峰值出现在上午10点左右，温度最低值出现在0点左右.因为当地云层稀薄，地面热量散失较快，当阳光直射时，空气温度在短时间内升至最高；当没有阳光照射时，气温急剧下降，表现出相比于平原地区温度峰值向后推移的规律.而隧洞内是一个相对密闭的环境，气温受到外界环境的影响较小，温度变化趋势与外界相同，但幅值随着入洞深度的增加而减小.

在隧道内各个断面布设测温计，实时监测各时刻温度随隧道深度的变化规律，现场选取6个样本进行研究，洞内温度变化规律如图4所示.

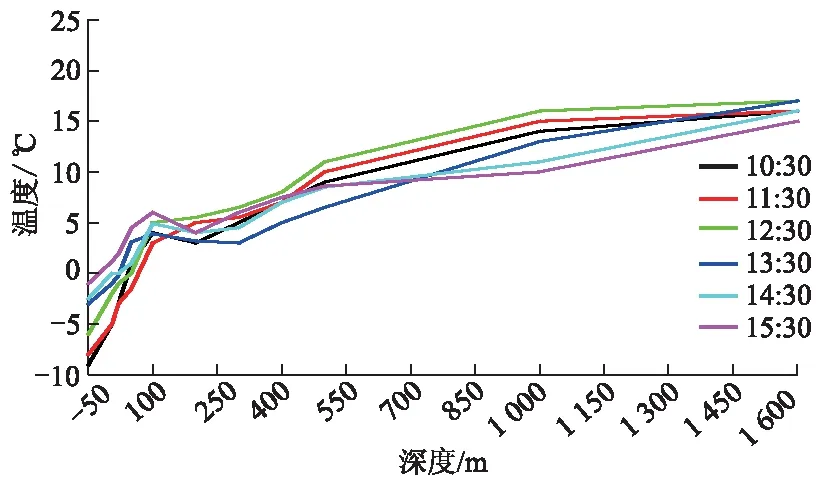
图4 洞内温度变化规律

由图4可知：隧道温度在距离洞口为0～100 m时上升最快，且在100 m处达到峰值，在100～300 m时出现下降趋势，300～1 600 m时温度持续上升，并趋于稳定；整体温度变化范围为-10～17 ℃，中部温度基本稳定在10～17 ℃.因为环境气温不断变化，洞口段产生对流，所以温度变化较快；在隧洞200 m处，设置有横通道，增加了左右洞空气的对流作用，因此在200 m左右温度出现下降趋势；洞深处空气几乎不与外界产生对流和热交换，受地热影响，达到一定的入洞深度后，温度持续升高，并趋于稳定.

2.3 隧道内围岩温度变化规律

选取4个测试断面对隧道围岩温度进行研究，围岩温度变化规律如图5所示.

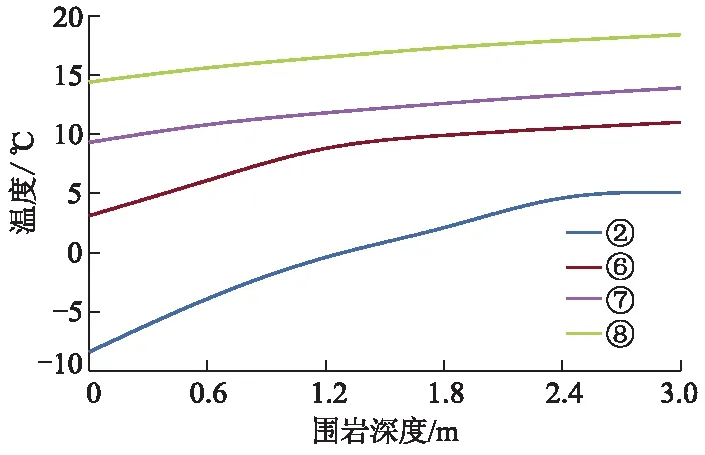
图5 围岩温度变化规律

由图5可知：随测试深度的增加，温度在围岩内呈现非线性上升的趋势；随着入洞深度增加，越靠近洞口的断面温度变化越明显.由于洞口围岩受环境影响较大，达到一定测试深度后，温度上升明显.而随着洞深的增加，地热对围岩温度变化的影响越来越大，在一定测试深度内围岩温度缓慢上升，并趋于稳定.

2.4 隧道内断面温度变化规律

同一隧道截面各部位的温度也会有所差异，这种变化会使二衬结构的内力更加复杂化.选取4个典型断面对二衬结构各部位进行测试，结果见图6.

图6 隧道断面温度变化规律

由图6可知：隧道②号断面各部位温度变化由大至小依次为拱顶、路面和边墙，⑥、⑦和⑧断面各部位温度变化由大至小依次为路面、拱顶和边墙；②号断面路面温度比拱顶低0.9 ℃，⑥、⑦和⑧号断面路面温度高于拱顶0.1～0.3 ℃，对于所有的截面拱顶温度均高于两侧边墙.究其原因如下：对于路面温度，②号断面受外界环境影响较大，气温升高时，路面首先解冻吸热，从而导致路面温度较拱顶低；⑥、⑦和⑧号断面中，由于水蒸气凝结于拱顶，造成拱顶温度略低于路面；两侧边墙的温度均小于拱顶与路面，这主要是由于隧道中下部空气流动方向与上部相反，在隧道截面中部存在复杂的对流作用，加剧了隧道边墙的热量散失.

3 隧道温度场模拟与分析

3.1 本构模型及基本假定

Drucker-Prager屈服准则是对Mohr-Coulomb准则的近似，它修正了Von Mises屈服准则.其屈服面并不随着材料逐渐屈服而发生改变，因此没有强化准则，塑性行为被假定为理想弹塑性.假定二衬结构外侧接触面与初支完全贴合，初支产生的接触压力垂直作用于结构表面，二衬混凝土材质均匀，各向同性，混凝土为理想材质.底部设置仰拱，仰拱在模型中仅起到二衬结构边界固定的作用，并不在温度及受力计算范围内，二衬结构内外侧均为自由边界状态.考虑其重力效应、接触压力和温度效应的影响，利用包含内变量的屈服准则描述混凝土材料的硬化和软化，通过在硬化参量的表达式中的温度变量来反映温度的影响[8-9].基于Drucker-Prager强度准则，构造如下的屈服函数：

(2)

(3)

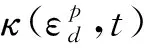
(4)

式中：a1和a2为温度软化因子，表征高温条件下混凝土材料力学性质的弱化，其表达式为

(5)

(6)

式中：f′为常温下混凝土抗压强度;t0为初始温度.

3.2 模型构建及网格划分

隧道截面特征较为明显，构建模型时假定沿纵向为无限延伸的状态，根据各断面温差及各部位接触压力的不同，模拟该断面受力及变形情况.二衬结构模型构建如图7所示.

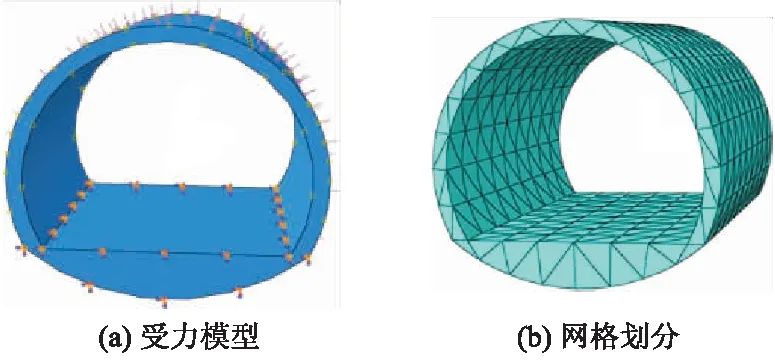
图7 二衬结构模型构建

根据实际条件对模型施加约束均如图7a所示，二衬结构围岩侧不同部位施加接触压力，结构内外侧设置不同温度.采用有限元法进行荷载应力分析时，模型尺寸越接近工程实际情况，网格划分越细，则计算结果与实际的相关程度越高[10].本研究中选取的模型尺寸如下：长度为30 m，净宽为10 m，净高为5 m，开挖面积为81 m2，二衬厚度为40 cm.模型单元采用C3D10(十结点二次四面体单元)进行网格划分如图7b所示.通过对不同模型长度进行收敛性分析，验证模型收敛性分析结果的可靠性，模型长度为10、30、50、70和100 m的温度应力分别为3.669、3.671、3.679、3.702和3.733 MPa.由此可见，在一定的洞深范围内，温度应力误差能够控制在2%以内，因此认为本模型完全能够达到工程应用的精度要求.

3.3 参数及数据分析

C40混凝土本构模型参数如表1所示，表中ρ为密度，E为杨氏模量，ν为泊松比.②和⑧号断面二衬结构各部位测试的温度如表2所示，表内数据为一天内二衬结构内、外侧温度最大差值，并非同一时刻的温差.②和⑧号断面二衬结构与初支之间的接触压力测试结果如表3所示，本研究中主要计算二衬结构自身的温度效应，二衬结构与初支之间的接触压力是围岩和初支作用于二衬结构的作用力，其温度效应远小于二衬结构本身，因此接触压力采用定值.

表1 C40混凝土本构模型参数

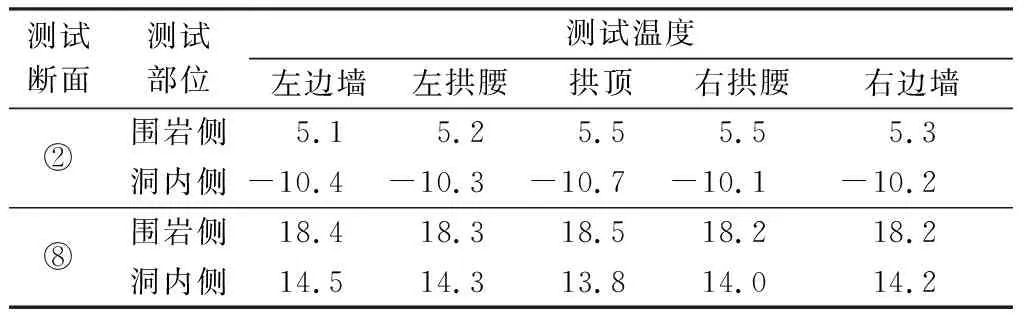
表2 围岩侧和洞内侧的温度 ℃

表3 二次衬砌结构接触压力 kPa

3.4 模拟结果与分析

热传导计算原理由Fourier定律给出，即由于温度梯度引起一个物体不同部分之间内能交换.根据热传导Fourier定律，热流密度公式为

(7)

式中：q″是热流密度，W·m-2；k是导热系数，W·(m·℃)-1.对②号断面建立温度分布模型见图8.

图8 二衬结构内温度分布云图

由图8可知，温度在二衬结构中呈梯度分布，围岩侧温度最高为5 ℃，内侧温度最低为-10 ℃，此时二衬结构内、外侧最大温差为15 ℃.②和⑧号二衬结构产生的温度应力及变形情况分别见图9、10.

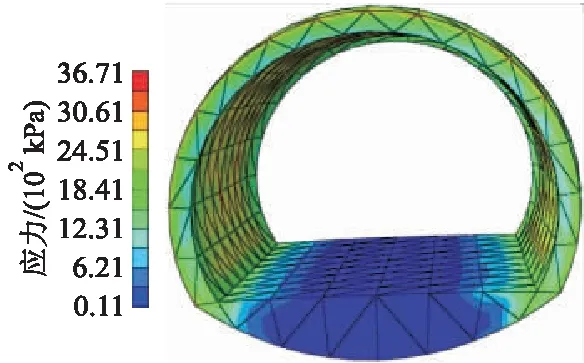
图9 ②号二衬结构温度应力云图

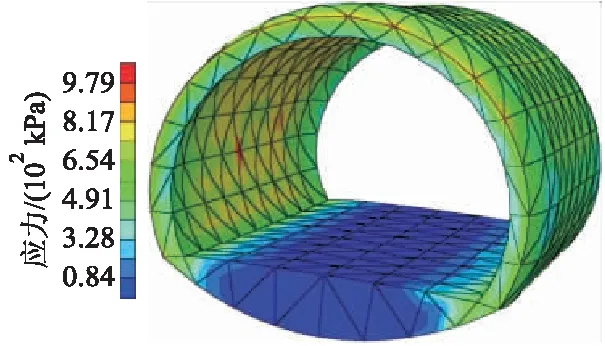
图10 ⑧号二衬结构温度应力云图

由图9和10可知：当二衬结构内、外侧产生温差时，在结构内部会受到温度应力的影响，使二衬结构内、外侧产生变形；②号断面受温差影响最大，最大温度应力σt1=3.67×103kPa，⑧号断面最大温度应力σt2=9.79×102kPa，两断面在二衬结构外侧均产生膨胀变形，考虑外部约束下及混凝土材料性质，结构膨胀变形受到围岩约束，二衬结构内侧将出现张拉裂缝.

由于隧道围岩性质及地质条件的不同，围岩压力并非均匀分布，因而导致作用在二衬结构的接触压力产生差异[11]，如表3所示.图11、12分别是②和⑧号断面二衬结构考虑接触压力和自重应力时的受力及变形情况.该隧道二衬结构所用C40混凝土的模型参数以及接触压力如表1和3所示，重力加速度g=9.8 m·s-2.

图11 ②号二衬结构应力云图

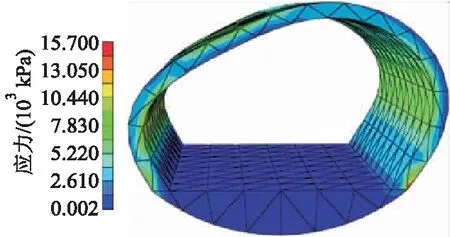
图12 ⑧号二衬结构应力云图

由图11和12可知：②和⑧号断面均受到偏压荷载的影响，②号最大应力σF1=2.93×104kPa，⑧号最大应力为σF2=1.57×104kPa；断面的衬砌结构受到偏压荷载的作用向右偏移，最大应力均出现在右侧拱脚位置，左侧拱腰均向内变形.接触压力在洞周不同部位相差较大，总体上应力由大至小依次为拱腰、拱顶和边墙，并表现出向内挤压的特征，受水平构造力影响较大.②和⑧号断面在温度应力、接触压力及自身重力耦合作用下结构的受力以及变形情况如图13和14所示.

由图13和14可知：在热力耦合作用下，二衬结构内应力均不同程度增大，②号断面最大应力σ耦1=3.05×104kPa，⑧号最大应力σ耦2=1.57×104kPa；热力耦合作用下，温度应力对于隧道变形有一定的缓解作用，但结构内应力均增大，并且温差变化越大，结构内应力变化越大，②号实际最大温度应力增大值Δσt1=1.22×103kPa，占总应力的4.00%，实际温度应力占比=(σ耦-σF)/σ耦×100%，⑧号实际最大温度应力增大值Δσt2=20 kPa，占总应力的0.13%，平均温差每增大1 ℃，温度应力增大至原来的2.71倍.GB 50010—2010《混凝土结构设计规范》中规定C40混凝土轴心抗拉强度设计值ft=1.71 MPa，而由温差引起的反复作用力，占到规范设计值的71.3%，这对于二衬结构是极为不利的.对于⑧号断面，温度应力占到规范设计值的1.2%，温差对于结构变形影响极小.考虑到二衬结构的疲劳破坏，因此当温差≥15 ℃时，必须对隧道结构采取防冻保温措施，结合高海拔地区温差曲线图(见图2)，可知3～10月温差一般小于15 ℃，可正常施工，其余月份温差多数超过该值，应当及时采取防冻保温措施.

图13 ②号耦合作用下二衬结构应力云图

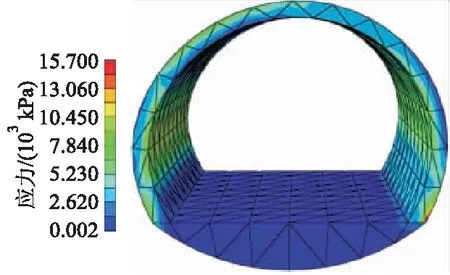
图14 ⑧号耦合作用下二衬结构应力云图

4 结 论

1) 隧道的年均气温及日均气温具有周期性，随时间呈正弦曲线变化，全年最大温差在1～2月，最小温差在7～8月，沿隧道纵深空气温度呈“快速增长—缓慢增长—趋于稳定”的变化规律，隧道洞内深度超过1 km以后，其温度基本保持恒定.

2) 越靠近隧道洞口的断面温度变化越明显，随着围岩深度的增加，温度趋于稳定，洞口断面各部位温度变化由大至小依次为拱顶、路面和边墙，而在超过某一深度后，各部位温度变化由大至小依次为路面、拱顶和边墙.

3) 隧道洞口段二衬结构受温差影响最大，温差越大，对隧道二衬结构的破坏越大，当日温差>15 ℃时，实际温度应力占二衬结构所受总应力的4.00%，由温差引起的反复作用力，占到规范设计值的71.3%，这对于二衬结构是极为不利的.分析认为在该地区3～10月可正常施工，其余月份日温差较大，最大日温差达到25.3 ℃，应提前对二衬结构采取防冻保温措施.