基于动态核PCA的复杂废水处理过程在线故障检测

刘鸿斌， 张 昊， 景 宜， 张凤山

(1. 南京林业大学 江苏省林业资源高效加工利用协同创新中心， 江苏 南京 210037； 2. 山东华泰纸业股份有限公司， 山东 东营 257335)

随着制浆造纸工业过程的日趋复杂化及生产规模的大型化，造纸过程中产生的废水问题也愈发凸显.造纸废水主要来自于黑液、白水等，其特点是水量大、浓度高、泡沫多及温度高，且非溶解性COD又为COD的主导成分，造成了水体的可生化性较差.此外，在造纸废水处理过程中存在诸如废液中残留的纤维、木质素及填料等较多干扰因素，造成Mg2+、Ca2+等离子与硫酸根、碳酸根及磷酸根离子形成钙化颗粒污泥，从而降低了废水处理反应器的处理能力.

在造纸废水处理过程中，集散控制系统(distri-buted control system, DCS)作为现代工业过程的控制平台被广泛运用.DCS系统使得过程中数据的采集量大幅增加，且DCS系统具有多闭环、强干扰及高耦合的特点，使得过程数据与故障信息之间无法得到清晰的逻辑关系[1].此外，过程中存在的耦合性、时变性等特征导致所采集的数据具有较强的非线性及动态特征，这为过程故障检测带来较大困难.废水处理过程的复杂性不仅造成故障检测难度的提升，而且使得整个系统中更加频发故障，极大地降低了污水处理效率及可靠性[2].这对于化工、石油等连续生产领域带来很大挑战，同时也对过程故障的及时发现提出更高要求.

针对以上问题，工业过程模型在过程监测等领域受到了广泛关注.过程建模方法主要分为基于数学模型的方法、基于知识的方法及基于数据驱动的方法.基于数学模型的方法针对复杂的工业过程往往难以建立准确的数学模型，使得该方法无法很好地应用于工业废水处理过程.此外，造纸废水处理过程的复杂性，也导致基于知识的方法在专家知识获取、自适应能力提高及实时性更新等方面存在较大缺陷，因此在实际运用中的通用性较差.相较于基于数学模型和基于知识的方法，基于数据驱动的方法不需要建立精确的模型，对于专家系统也无较强的依赖性，仅仅根据工业过程的历史数据，对数据中的信息进行深度挖掘，从而进行过程建模分析，以此实现过程故障检测的目的.因此基于数据驱动的方法被广泛用于复杂过程的故障检测及诊断.

传统的统计过程监测包括单变量和多变量统计监测.单变量过程统计主要包括Shewhart控制图和指数加权移动平均控制(exponentially weighted mo-ving average, EWMA)图等[3].然而单变量过程统计监测只考虑了过程中单一变量的变化，不能对多变量之间的相关性进行准确描述，在实际应用中无法满足现代造纸废水处理过程的监测要求.为了克服单变量在过程监测中存在的缺陷，多变量统计过程监测方法在20世纪90年代初运用于过程监测及故障诊断.多变量统计过程检测方法主要包括多元线性回归(multiple linear regression, MLR)[4]、主成分分析(principal component analysis, PCA)[5]及偏最小二乘(partial least squares, PLS)[6].然而传统的线性方法以满足线性关系为前提，且变量之间需以互相独立为条件[7]，因此传统的多变量故障检测方法无法较好适应非线性动态系统，易出现过程故障信息误报，甚至发生事故[8].针对过程中普遍存在的时变性，文献[9]首次提出动态PCA方法，该方法在建模过程中考虑了过程的相关性，提高了动态过程描述的准确性，但该方法在处理非线性过程变量时，不能进行非线性投影，造成故障检测过程中出现误报率较高的情况.为了克服变量之间存在的非线性问题，文献[10]提出核PCA方法，但该方法未考虑实际工业过程普遍存在的动态特性，导致对故障检测灵敏度不高，因此在运用中存在一定局限性.

为此，笔者将PCA方法与核函数相结合，利用高斯核函数的非线性映射来解决数据非线性问题，并通过构造增广矩阵及引入时滞系数的方法来嵌入动态模型，以此更好地描述过程的动态特征.在偏移、漂移及精度下降3种故障下，分别采用PCA、核主成分分析(kernel principal component analysis, KPCA)及动态核主成分分析方法(DKPCA)进行对比分析，以此来探究DKPCA方法在复杂造纸废水处理过程中的有效性.

1 方法原理

1.1 主成分分析

主成分分析(PCA)作为一种多变量统计分析方法，其基本思想是将高维数据投影至低维数据[11].PCA模型通过建立主元子空间和残差子空间，将数据样本投影到子空间上，并在两个子空间上分别建立T2统计量及平方预测误差(squared prediction error,SPE)统计量.

假设数据样本为X=[x1,x2,…,xn]T∈Rn×m，n为样本数，m为变量数，其协方差矩阵定义为Σ=XTX/(n-1)，利用PCA方法建立统计分析模型：

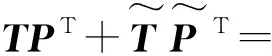
(1)

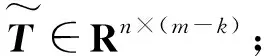
(2)

对式(1)两边同乘负载向量pi，可以得出主元向量ti为数据样本X在负载向量pi上的投影，即

ti=Xpi.

(3)

由式(3)可得主元向量，即为原始数据样本X在负载向量pi上的投影，投影越大，则表明所包含样本数据中的原始信息越多.通过PCA方法分解后，原始数据X变量空间维度由m降至k，且变量之间互不相关[12]，实现了低维度的多元统计分析.

1.2 核主成分分析

在实际工业过程中，数据普遍存在较强的非线性特征，使得传统PCA在解决该类问题时存在较大的局限性，因此相关学者提出核主成分分析(KPCA).KPCA方法用非线性映射将数据从原始数据空间映射到特征空间，从而在特征空间进行PCA统计方法的分析，利用统计量指标衡量故障检测率.KPCA方法关于核函数的选择主要包括线性核函数、多项式核函数及高斯核函数等，其中，由于高斯核函数具有所需要调整的参数较少等优点被广泛使用.笔者利用高斯函数K(xi,xj)=exp(-‖xi-xj‖2/c)作为核函数，‖·‖为l2范数，c为高斯函数带宽.假设数据样本为X=[x1,x2,…，xn]T∈Rn×m，通过非线性映射函数将原始数据进行投影，非线性映射关系为

x∈Rm→Φ(x)∈Rh，

(4)

式中：Φ(·)为非线性映射函数；m为原始空间数据维度；h为特征空间数据维度，且h通常较大.

首先计算特征空间中数据的协方差矩阵：

(5)

协方差矩阵Σφ对应的特征方程为

λv=Σφv，

(6)

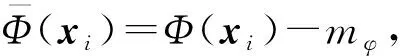
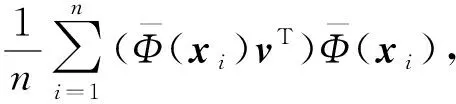
(7)

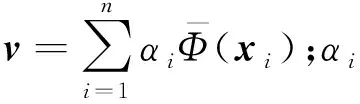
(8)

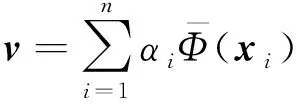
(9)

将式(7)进一步化简为

(10)

特征空间中的新样本xnew对应得分向量计算式：

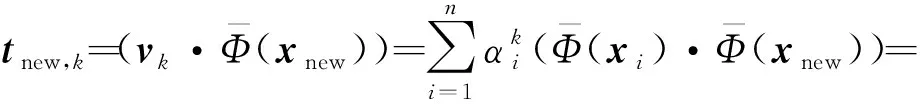
(11)

式中：k=1,2，…,p,p为KPCA中所选择的主元个数.

1.3 动态核主成分分析

利用非线性映射将原始空间数据映射到特征空间，并在特征空间中利用PCA建立统计分析模型，一定程度上优化了PCA无法克服非线性数据的问题.然而实际造纸废水处理过程普遍具有时变性等特征，使得不同变量之间存在序列相关性[13].因此在KPCA算法基础上通过构建动态模型，提出动态核主成分分析(DKPCA)方法，以此提高动态过程中故障检测的准确性.动态模型如下：

数据样本X的原始矩阵为

(12)

增广矩阵定义为

X(l)=

(13)

式中：t为时间序列中某一时刻；d为时滞变量.

通过引入动态方法，使得故障检测模型对数据的动态结构有更强的捕捉性能，对模型的过程监测性能有一定的改善.统计量指标用来实现故障检测准确率的分析，常用的统计量指标是平方预测误差(SPE)[14]，其控制线为过程检测临界值，当检测值超过控制线，则系统会将超过控制线的检测点认为是故障.SPE统计量控制线定义为

(14)

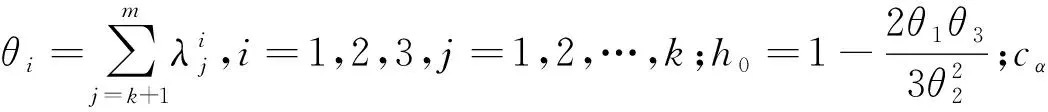
2 结果与讨论

2.1 造纸废水处理

2.1.1 废水数据

数据取自广东东莞造纸厂好氧段废水处理工况[15].图1为造纸废水处理过程数据.共170组数据，分别为流量(Q)、进水化学需氧量(w(COD)in)、出水化学需氧量(w(COD)eff)、进水悬浮固形物(w(SS)in)、出水悬浮固形物(w(SSeff))、溶解氧量(w(DO))、温度(t′)及pH值.

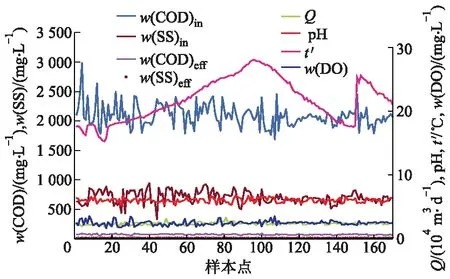
图1 造纸废水处理过程数据

2.1.2 废水处理过程

造纸废水处理工艺采用活性污泥法，利用悬浮生长的微生物絮体处理有机废水，其处理流程如图2所示.该系统由沉淀池、曝气池及污泥回流系统组成.制浆造纸生产过程中产生的废水首先进入初沉池过滤掉部分杂质，由初沉池处理后的上层废液进入曝气池，发生氧化反应，通过活性污泥与废水进行充分接触与混合，使得水体中可溶性有机物被吸附，并被水体中微生物群所分解.处理后废水进入二沉池，将活性污泥与废水进行分离，并将一部分污泥回流至曝气池.

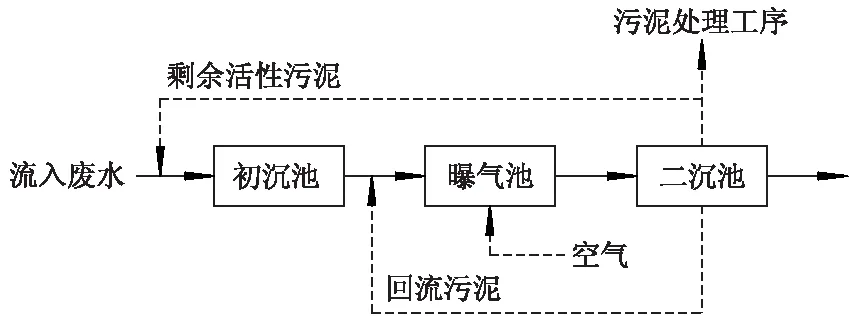
图2 好氧废水处理过程

2.2 故障构建及结果分析

针对造纸废水处理过程的复杂性，笔者构建了偏移故障、漂移故障及精度下降故障3类故障模型.偏移故障是基于正常工况数据加上原始变量数据均值的20%来构建故障(w(COD)in(t)+418)；漂移故障是以原始数据加上时间乘以0.05得到的数据来构建故障(pH(t)+0.05t)；精度下降故障是在原始变量的基础上加入均值为30、方差为1的正态随机噪声的方式构建故障数据(w(SS)eff(t)+N(30,12))；将样本数据的前110组样本点作为训练集，后60组样本点作为测试集.故障构建图如图3所示.

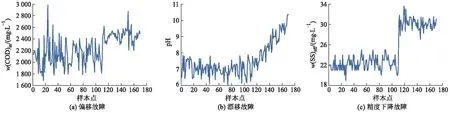
图3 3类故障数据

基于PCA、KPCA及DKPCA等3种过程监测方法，对造纸废水处理过程进行故障检测分析.不同方法的故障检测率如表1所示.基于PCA、KPCA及DKPCA等3种方法的故障检测图如图4-6所示.红色虚线为置信度为95%的控制线，超过红线则表示故障被准确检出，本研究采用SPE统计量来表征故障检测的准确性.

由表1可知：在SPE统计量指标下，相较于PCA及KPCA，在偏移故障中，DKPCA方法的故障检测率分别提升了96.96%及87.87%；在漂移故障中，KPCA未检测出故障，DKPCA的故障检测率相较于PCA提升了5.12%；在精度下降故障中，PCA及KPCA方法故障检测率均为100%，但DKPCA方法下降至68.33%.

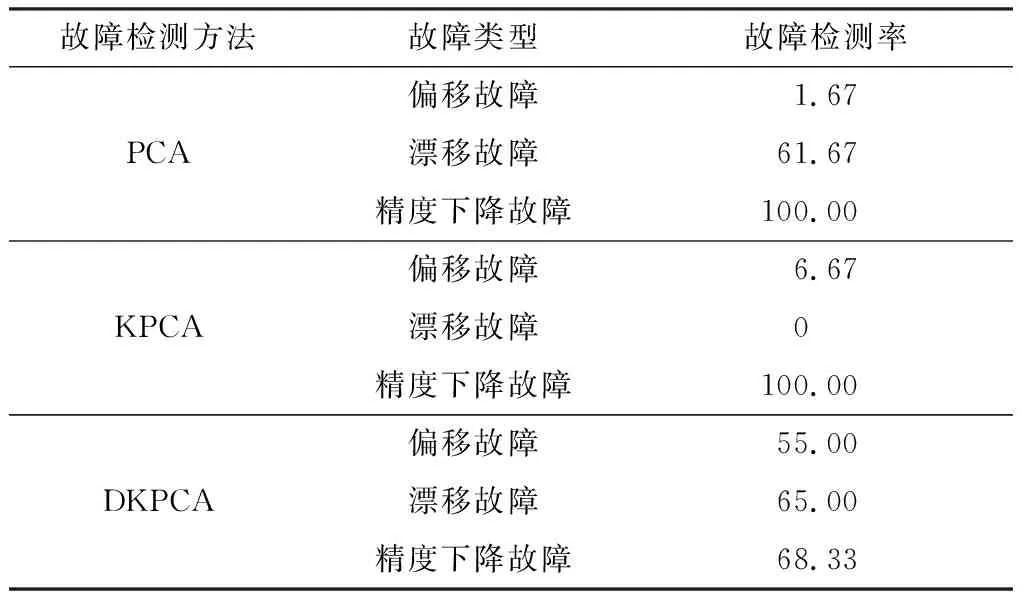
表1 SPE指标下3种方法的故障检测率比较 %

由图4-6可知：漂移故障中，相较于PCA方法，DKPCA方法故障检测率仅提升了5.12%，但DKPCA通过动态方法的引入，对于复杂过程的动态特性有着更强的捕捉能力，对故障检测的灵敏度也更高；DKPCA在初始出现故障时就可立即检测出故障，而PCA方法在第16个样本点处才检测出故障，因此动态方法对于在线故障检测的灵敏度有一定的改善；PCA及KPCA在精度下降故障下检测率均为100.00%，而DKPCA检测率为68.33%，得出DKPCA对于精度下降等此类微小故障的检测有一定的局限性.

图4 基于SPE指标的PCA故障检测结果

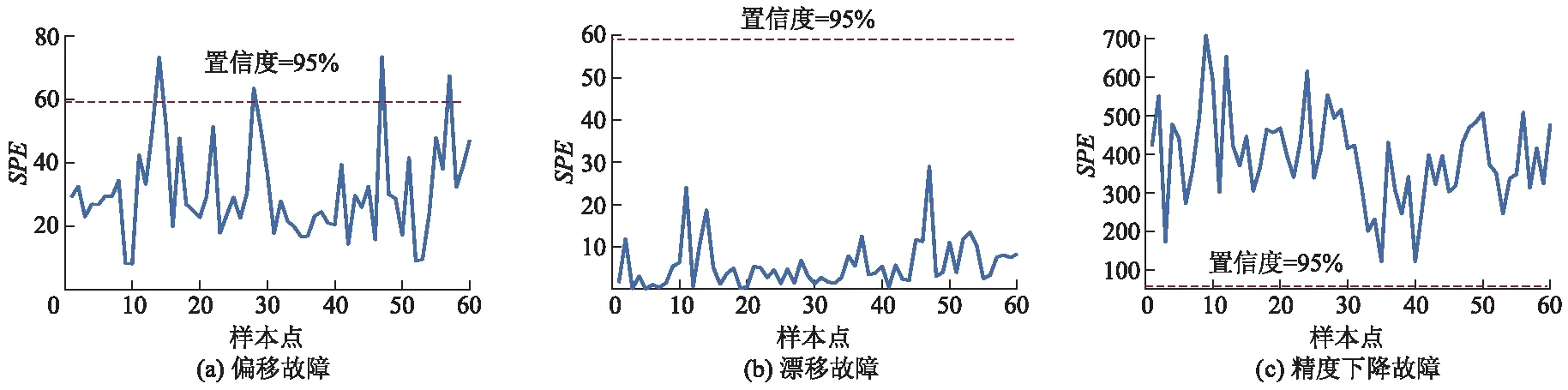
图5 基于SPE指标的KPCA故障检测结果

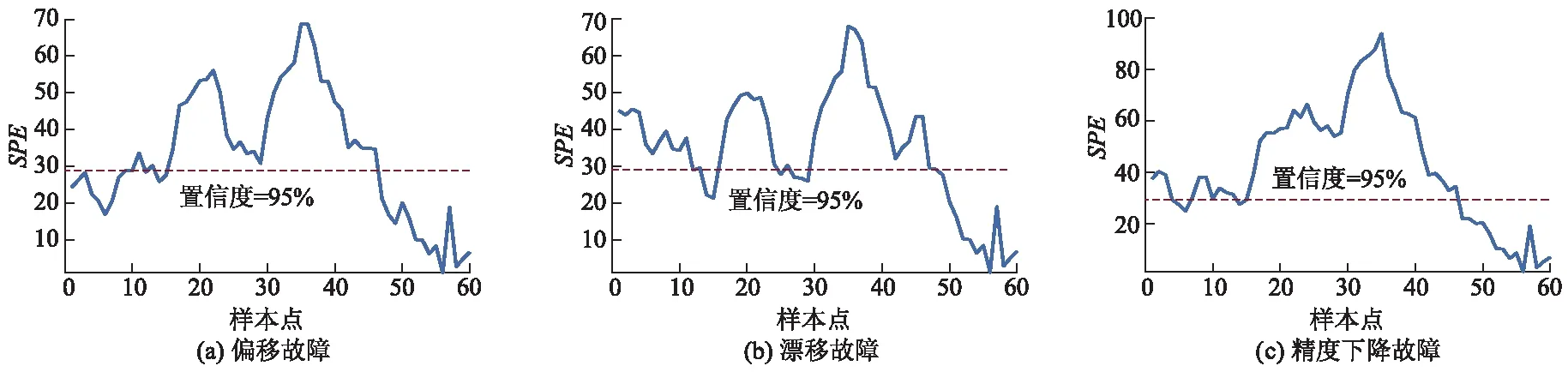
图6 基于SPE指标的DKPCA故障检测结果

3 结 论

1) 将动态技术与传统静态故障监测方法结合，表明了动态模型在故障监测中的有效性.

2) 在传统PCA和KPCA基础上提出了动态核主成分分析(DKPCA)方法，有效克服了过程数据存在的非线性及动态特性.

3) DKPCA方法在偏移故障下相较于传统的PCA及KPCA方法，其故障检测率分别提升了96.96%及87.87%，有效地提高了故障检测率.

4) DKPCA方法对于故障检测更为迅速，提高了在线检测的灵敏度及可靠性.通过动态技术及核函数的引用，有效解决了传统方法无法克服过程的非线性及时变性的问题，提高了实际工业过程检测的准确性及灵敏度.