论任意速度下导弹追击轨道的求解与条件

高浩渊

（陕西科技大学，陕西 西安 710021）

0 研究背景和研究方法

目前，有关导弹追击的研究包括多倍速导弹追击轨道[1]和制导系统运用[2]。其中，仅通过解微分方程组来求解ESR 模型[2]存在方程难以求解或者出现无意义解的问题，也忽略了导弹速度小于目标速度时根本不能成功拦截的情况。该文通过构建ESR 模型中相同条件模型的理论，给出了在该模型中判定和求解任意速度下导弹追击轨道方程和时间的可行方法。

该文所使用的研究方法包括近似建模和优化算法，这些也是在导弹总体设计优化过程中实现一体化优化的关键要素[3-8]。求解问题时运用求导链式法则、换元积分法、分离变量法和物理量纲分析；数值计算时运用MATLAB 求解高次方程和微分方程。该文研究的重点是基于优化方案合理地对现实问题进行抽象，建立近似模型，得到有速度参数的轨道方程，并给出对速度参数赋值计算轨道方程和打击时间的方法，从而讨论所需的条件。

ESR 模型：目标以恒定速率v在xy平面内沿y=xtanφ+b的直线飞行（φ 为目标运动方向与x轴方向的夹角；b为常数），当时间t=0 时，在（h′，0）点。导弹在t=0 时从原点出发，以恒定的速率V 运动，速度方向始终指向目标。求导弹的运动轨道和击中目标的时间可以转化为以下模型进行求解。

1 以垂直距离为导弹发射条件模型

1.1 无引力场的导弹追击模型

当φ=π/2 时，目标以恒定速率v在xy平面内沿x=h向y正半轴方向直线飞行，当时间t=0 时，在（h，0）点。导弹在t=0 时从原点出发，以恒定的速率V运动，速度方向始终指向目标。根据以上初始条件便可以求出导弹的运动轨道和导弹击中目标的时间。设t时刻导弹位于（x，y），此时目标位于（h，vt）点，如公式（1）、公式（2）所示。

用x对公式（2）的两端求导得到公式（4）。

公式（7）为导弹的轨道方程。

当导弹击中目标时，导弹与目标同时位于（h，vt）点，将y=vt、x=h代入公式（7）得到公式（8）。

公式（8）为导弹击中目标的时间。

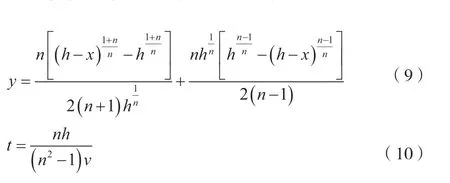
当V=nv（n为正整数）时[1]，化为多倍速导弹的追击轨道方程和打击时间，如公式（9）～公式（10）所示。

对公式（7）～公式（8）进行物理量纲分析发现，该模型中的导弹轨道方程和打击时间函数在物理学条件下成立。根据公式（8）可以发现：当V＜0 时，t＜0，即导弹不能成功拦截或击中目标。同理，当V=0（即导弹没有发射）时，t=0，即意味只有目标经过原点时才能成功拦截目标；只有当V＞v时，导弹才能成功拦截或击中目标。如果要使导弹在一定时间内能成功拦截或击中目标，即有给定时间T，根据公式（8）可以得到公式（11）。

从公式（12）中可以发现，在不清楚敌方目标速度的情况下，己方的导弹速度自然是越高越有把握在一定时间内击中目标。

1.2 有引力场的导弹追击模型

目标以恒定的水平速率v在xy平面内向y轴正半轴方向飞行，受到沿x轴负半轴方向大小为g的重力加速度（进行平抛运动），当时间t=0 时，在（h，0）点。导弹在t=0 时从原点出发，在受到同样的沿x轴负半轴方向大小为v的重力加速度的情况下，以初速率V运动，速度方向始终指向目标。根据以上初始条件便可以求出导弹的运动轨道和导弹击中目标的时间。可以证明的是，如果目标与导弹位于相同的引力场下，导弹击中目标的时间不变。

导弹击中目标时的坐标和时间如公式（13）所示。

2 以圆形半径为导弹发射条件模型

2.1 当cosφ＜0时，转化成求解模型

2.1.1 导弹成功拦截目标

导弹成功拦截目标，即将y=r2h2--vt、x=h代入公式（18）得到公式（19）。

公式（19）为导弹击中目标的时间。同理，对公式（19）进行物理量纲分析可以发现，该模型中的打击时间函数也在物理学条件下成立。从中可以发现，只有当V和v满足公式（20）的条件时，导弹才能够成功拦截目标。

可以通过MATLAB 在给定数值的情况下进行判定（具体方法如程序1 所示）。用MATLAB 判定是否满足不等式的程序1（在MATLAB 中输入以下程序）。

＞＞ syms V v h r H#设置变量#

＞＞V=3，v=1，h=10，r=100；#给变量赋值，对其他数值的计算只需把相关数字代入即可#

ans =

1 #其中1 表示成立，0 表示不成立。#

程序1 的结果意味当V=3、v=1、h=10 且r=100 时，不等式成立，导弹在这种条件下能成功拦截目标。

2.1.2 导弹没有击中目标

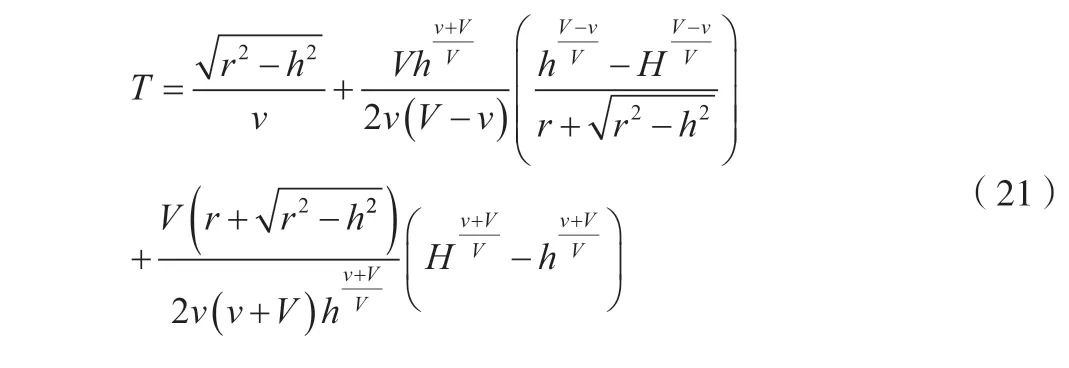
对公式（21）进行物理量纲分析发现，该公式有时间的量纲，因此该公式在物理学条件下成立。从中可以发现，当V=0时，意味导弹在目标移动到与导弹的最短距离前没有发射，即可转化为以垂直距离为导弹发射条件的模型（h为导弹沿x轴正半轴方向与目标的距离），如公式（22）所示。

联立公式（21）和公式（23）可得到关于H的方程。

诗人感慨现实中缺少后羿这样的英雄。月亮既然已经沦没而迷惑不清，还有什么可看的呢！可诗人心中的忧愤反而加深了，不忍一走了之，忧心如焚。

事实上，可以通过MATLAB 来求解H的值，因为该方程为高次方程，所以没有通解，但可以通过给V和v赋值来进行数值计算，解出H的近似值（具体方法和计算如程序2 所示）。当H没有非负实数解时，意味导弹成功拦截目标，从而转化成2.1.1 节所述的方法来求解。如果H有非负实数解，则如公式（24）所示。

公式（24）为拦截所用的总时间。值得一提的是，如果要求在时间T内功成功拦截目标，那么在V＜v且V、v满足公式（25）时得到关于最低成本的最优解。

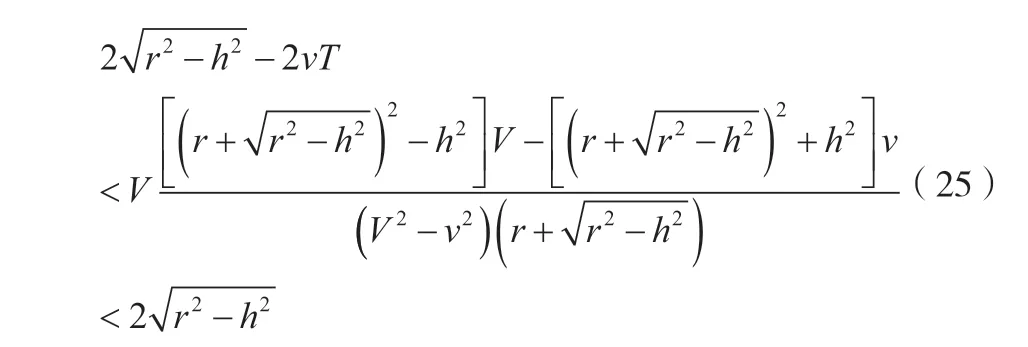
用MATLAB 为H赋值并求解的程序2（在MATLAB 中输入以下程序）。

-15.5367 + 2.1040i#可知此条件下H 无实数解，方程不成立，导弹拦截成功#

程序2 的结果意味当V=213.23、v=445.6、h=12 且r=57 时，方程解无实数，方程不成立，即H不存在，导弹在y=r2h2--vt之前就与目标相撞，只有当方程的解为非负实数时，得出的结果才为H的值。只需要再将数值代入公式（19）即可得到导弹击中目标所用的时间。当解出的时间大于0 时，得出的结果为拦截所用的时间，否则意味导弹不能成功拦截目标。

2.2 当cos φ＞0时转化成模型的求解

公式（31）为导弹击中目标的时间。对公式（31）进行物理量纲分析可知，该模型在物理学条件下成立。从中可以发现，只有当V、v满足公式（32）的条件时，导弹才能够成功拦截目标。

可以在给定数值的情况下用计算机来进行判定（具体方法如程序3 所示）。

用MATLAB 判定是否满足不等式的程序3（在MATLAB中输入以下程序）。

＞＞ syms V v h r H#设置变量#

＞＞ V=3，v=1，h=10，r=100；#给变量赋值，对其他数值的计算只需把相关数字代入即可#

＞＞V*（（（r+（r^2-h^2）^（1/2））^2-h^2）*V+（（r+（r^2-h^2）^（1/2））^2+h^2）*v）/（（V^2-v^2）*（r+（r^2-h^2）^（1/2）））＞2*（r^2-h^2）^（1/2）

ans =

1 #其中1 表示成立，0 表示不成立。#

程序3 的结果意味当V=3、v=1、h=10 且r=100 时，不等式成立，导弹在这种条件下能够成功拦截目标。只需要将相应的数值代入公式（31）就可以解得导弹成功拦截目标所用的时间。

3 结语

该文通过建立以垂直距离和圆形半径为导弹发射条件的模型来解决在ESR 模型中任意速度下导弹追击的轨道和时间问题，并对这些轨道方程和时间函数进行分析，得到了导弹成功拦截目标的必要条件和相关数值计算的方法。从工程技术的角度来看，这些模型中的导弹轨道公式过于理想，但是通过利用这种最优化方案可以从复杂的物理现象中合理地抽象出理想的数学模型，最终运用一系列计算手段和方法找到最优化解。该文所论述的模型的计算方法和条件对未来我国太空反导防御系统的设计具有一定的实际意义。