Artificial equilibrium points and bi-impulsive maneuvers to observe 243 Ida

Alln Krdec de ALMEIDA Jr, Gerldo Mgel Couto OLIVEIRA,Antonio Fernndo Bertchini de Almeid PRADO

a National Institute for Space Research (INPE), Sa˜o Jose´ dos Campos 12227-010, Brazil

b Federal Center for Technological Education of Minas Gerais (CEFET-MG), Belo Horizonte 30421-169, Brazil

KEYWORDS Artificial equilibrium points;Astrodynamics;Orbital transfers;Solar radiation pressure;Solar sail

Abstract In the restricted three-body problem, the traditional Lagrange points L1 and L2 are the only equilibrium points near the asteroid 243 Ida.The thrust generated by a solar sail over a spacecraft enables the existence of new artificial equilibrium points,which depend on the position of the spacecraft with respect to the asteroid and the attitude of the solar sail.Such equilibrium points generate new spots to observe the body from above or below the plane of motion.Such points are very good observational locations due to their stationary condition. This work provides a preliminary analysis to observe Ida through the use of artificial equilibrium points as spots combined with transfer maneuvers between them.Such combination can be used to observe the asteroid from more different points of view in comparison to fixed ones.The analyses are made for a spacecraft equipped with a solar sail and capable of performing bi-impulsive maneuvers.The solar radiation pressure is used both to maintain the equilibrium condition and to reduce the costs of the transfers and/or to create transfers with longer duration.This is a new aspect of the present research,because it combines the continuous thrust with initial and final small impulses, which are feasible for most of the spacecraft, because the magnitudes of the impulses are very low. These combined maneuvers may reduce the transfer times of the maneuvers in most of the cases,compared with the maneuvers based only on continuous thrust.Several options involved in these transfers are shown,like to minimize the fuel spent(Δv)as a function of the transfer time or to extend the duration of the travel between the points.Extended transfer times can be useful when observations are required during the transfers.

1. Introduction

The equilibrium Lagrange points that appear in the circular restricted three-body problem have several practical applications. They are five points of equilibrium, which means that a spacecraft placed there with zero velocity can remain there for long time through the use of a secondary control system that will not be taken into consideration here.This manuscript considers the Sun and the asteroid Ida1-3- a celestial body located in the asteroid belt-as the main bodies for the Circular Restricted Three-Body Problem(CRTBP).In the absence of a thrust, the traditional Lagrange pointsL1andL2are the only equilibrium points near the smaller primary.The main goal of the present paper is to propose a new technique of maneuvers,so we start with the circular model, which is simpler. The eccentricity of the orbit of Ida around the Sun is 0.041, which is not too large. Of course, if more accurate results are required, the elliptic restricted three-body problem is recommended.4The problem is that this model gives results for specific values of the true anomaly of Ida in its orbit around the Sun, which would extend too much the present study. Since this is the first study considering this type of combined maneuvers, we choose to use the circular model and leave the eccentric model for further studies.The differences between the two models do not impact in the conclusions, they just give some more accuracy for the results, in the case Sun-Ida-spacecraft.Of course, it makes larger differences in more elliptic systems.

Using a general thrust, new configurations of equilibrium may arise, which are the so called ‘‘Artificial Equilibrium Points” (AEPs).5-13The recent technological development of new lightweight and highly reflexive materials makes possible the use of solar sails14to generate the thrust required to achieve many general AEP in space.15,16Important missions used these materials, like NanoSail-D2,①https://directory.eoportal.org/web/eoportal/satellite-missions/n/nanosail-d2.Ikaros,17or LightSail-2.②https://directory.eoportal.org/web/eoportal/satellite-missions/content/-/article/lightsail-2.

Thus,the use of a solar sail gives new configurations for the equilibrium points,based on the position and inclination of the vector normal to the solar sail, i.e. its attitude. A solar sail allows a spacecraft to park at a closer distance to the secondary main body than the traditionalL1orL2. Besides that,new perspectives for viewing from above or below the plane of motion can be reached through the use of a solar sail to observe the body from a stationary condition.9,18-22

The idea of placing a spacecraft fixed in locations near the polar region to observe better a celestial body is not new. It was suggested to observe the Earth in Refs. 23,24 or other planets as well.25The use of solar sails has also been studied before in missions to asteroids.26Refs. 27,28 show that solar sails are especially interesting for rendezvous missions of a spacecraft with several asteroids, because there is no need to carry large amounts of on-board fuel.They also show hovering points and trajectories around some asteroids. Another publication considering solar sails in the restricted three-body problem can be seen in Ref. 29. Solar sail transfers between AEP has been studied in Refs. 30-32.

The present paper studies control and orbit transfer of a spacecraft equipped with a solar sail traveling in the circular restricted Sun-Ida system. Fixed points and their stability are considered in the paper, showing that they are not linearly stable in at least one direction, and thus control techniques are required to maintain the hover. Lyapunov stability under minimum control condition can be applied for a spacecraft through the use of a constant thrust.33Stability studies for the case of an oblate spheroid34and for a thrust in the radial direction11are available in the literature. Another option is to put the spacecraft in orbits around unstable AEP so that it is maintained near the fixed point for longer time.35-37The motion of a solar sail around AEP is also studied in Ref. 38.The fuel expenditure required to keep the spacecraft in the equilibrium points depends largely on the masses of the bodies involved. It means that the values for asteroids will be much smaller when compared to systems like Earth-Moon and Sun-Earth, so it is much more practical to use those points in the applications shown in the present paper.

The concept of finding artificial equilibrium points near asteroids has been recently explored in the literature,including double asteroid systems.39This paper also includes the calculations of displaced periodic orbits in these systems,whose mathematical model used is based on the Hill plus solar radiation pressure problem and the bi-circular four-body problem plus solar radiation pressure for the binary systems. They found pole-sitter-like orbits for the binary system 1999 KW4.Models based on the Hill problem avoid numerical problems due to the large differences in the masses involved, which is an alternative to make a rigid control of the accuracy of the numerical integrations. The Lambert perturbed problem using the Hill approach is investigated in Ref. 40. The Hill’s equations can be used to describe a spacecraft near an asteroid41particularly in the case where the solar radiation pressure is added to the problem.27,42However, the radius of the Hill’s sphere restricts the validity of the model, and its value is the distance of the two nearest collinear equilibrium points from Ida when no solar radiation pressure is taken into account.27In the case of the Sun-Ida-spacecraft system studied in this paper, this radius is only 9064 km.27It will be seen later in this paper that,in our results,when considering transfers between the artificial equilibrium points for longer time, the trajectory of the spacecraft may include paths whose distance from Ida may far exceed this value.Hence,the CRTBP is the model used in this paper.

The main idea of this manuscript is to offer new perspectives for the observation of Ida using new AEP to place a spacecraft equipped with a solar sail and to calculate the costs to transfer the spacecraft between these different equilibrium points, with the goal of giving some options to minimize the fuel consumption of these transfers. Those maneuvers are important, because they can make the spacecraft observe the system from different perspectives, so giving more scientific output for the mission.

In fact,the locations of the AEPs are functions of the areato-mass ratio of the spacecraft and the orientation of the solar sail.Therefore,by varying these parameters,it is found a family of AEPs, which can be represented by lines of solutions,instead of single points.

After finding the locations of the AEPs, the present research focuses on making orbital maneuvers transfer the spacecraft among those points and the traditionalL1andL2equilibrium points. There are several techniques available in the literature to make these maneuvers, as shown in Refs.16,24,29,39,43-49. Regarding the control available in the spacecraft, a space mission has many constraints, so it is important to have options for the trajectory control. The present paper shows a new approach, based on a bi-impulsive maneuver that applies the impulses at the end points involved in the transfer,but that uses the solar radiation pressure during the transfer to minimize the magnitude of the impulses applied.The reason is to explore a new approach,a combination of biimpulsive maneuver and solar radiation pressure,to give more options for a mission designer.

In that sense,the present paper has the goal of adding some new aspects to the existing literature: (A) obtaining artificial equilibrium points for the system Sun-Ida-spacecraft, which are important for observational operations; (B) proposing a new type of orbital maneuvers that combines the continuous thrust provided by the solar radiation pressure of the solar sail with the application of initial and final small impulses to the spacecraft. This technique has the disadvantage of requiring an impulsive engine available to the spacecraft, but this is not so difficult for most of the cases,considering that the magnitudes of the impulses are very small. On the other hand,these combined maneuvers may reduce the transfer times of the transfers in most of the cases, compared with the maneuvers based only on continuous thrust,and also give more flexibility to the maneuver,so giving more options to the mission.A detailed analysis of its use has to be made by the mission designers for specific situations. The goal of the present paper is to propose and shows some of the benefits of the maneuver.

2. Mathematical model

The mathematical tools used in this research are shown in this section.The mathematical description of the Artificial Equilibrium Points (AEPs) is shown in Subsection 2.3. The dynamics of the system for the transfers between different AEPs are explained in Subsection 2.4. The possible configurations of the solar sail during the transfers are shown in Subsection 2.5.

2.1. Rotating frame of reference

Two massive bodiesM1andM2are rotating around their barycenter in circular orbits with angular velocity ω with respect to an inertial coordinate system. A rotating frame of reference with axes （xr，yr，zr） is defined such thatM1andM2are on thexraxis,thezraxis is in the direction of their angular velocities around their barycenter, and theyraxis is according to the right hand rule. A spacecraft is subject to the gravitational interaction ofM1andM2plus a thrust fs. Its equations of motion in the rotating frame of reference is50,51

where r=［xr，yr，zr］ is the position of the spacecraft; r1and r2are the positions of the spacecraft with respect toM1andM2,respectively;r1=‖r1‖;r2=‖r2‖; μ1and μ2are the gravitational parameters ofM1andM2, respectively;mis the mass of the spacecraft.

The new parametersd1andd2defined below are the distances ofM1andM2from their barycenter, whose values are given by

whereRis the distance between the massive bodies. The vectors r1and r2can be written as

2.2. AEPs for a planar solar sail in the solar system

In this case,M1is the Sun andM2can be any body rotating around the Sun. In the case where the spacecraft is equipped with a planar solar sail,fsis the force over this planar solar sail due to the solar radiation pressure. In the case of a perfect reflection, this force is given by18

whereAis the area of the solar sail that reflects the solar rays,Reis the reference Sun-Earth distance,peis the value of the solar radiation pressure over the Earth (at a distanceRefrom the Sun), n=［nx，ny，nz］ is a unitary vector normal to the planar solar sail pointing upwards from the reflecting surface,and γ is the angle between nand the direction of the solar rays.In this work, since we deal with AEPs far from the Sun and close to thexraxis, for clarity purpose, we assume that the solar rays are parallel to thexraxis. Hence, γ is the angle between n and thexraxis. A drawing of the bodies and the solar rays relative to thexr-zrplane of the frame of reference is shown in Fig. 1.

A new parameterkpis defined askp=2peR2eA/m. Thus,using the thrust for a solar sail given by Eq. (6), the equilibrium condition given by Eq. (5) becomes

2.3. AEPs in the Sun-Ida system

In the case of the Sun-Ida system,M1is the Sun andM2is Ida.The distances of the bodies to their barycenter ared1=9×10-3m andd2=R-9×10-3m. Therefore, for this system, the approximationsd1=0 andd2=Rare used, i.e.the barycenter of the system is on the center of mass of the Sun.Note that we assumed circular orbits for the main bodies in the previous subsection. On the other side, the eccentricity of the orbit of Ida around the Sun is 0.041.53Thus,our model is a reasonable approximation of the real system. In this system, we replace r1→r, r2→rida, μ1→μsand μ2→μi, where rida=［xr-R，yr，zr］ is the position of the spacecraft with respect to Ida, whereRis the Sun-Ida distance,rida=||rida||,μsis the gravitational parameter of the Sun,and μiis the gravitational parameter of Ida.The angular velocity of the rotating frame of reference is approximated to ω=

Fig.1 Positions of bodies relative to the xr-zr plane of the frame of reference.

The AEPs are fixed points for the equations of motion.Using the above considerations and the thrust for a solar sail given by Eq. (6), the equilibrium condition given by Eq. (7)for the Sun-Ida system can be written in vector matrix form as

wherer=‖r‖. The AEPs shown in this paper reach values ofzrfar fromzr=0,and theirxr-yrcoordinates are still near thexr-yrplanar coordinates of Ida (they are placed ‘‘above” Ida).Such kind of orbits above the orbital plane are known as polesitter-like orbits,39and they provide a privileged point of view of Ida that cannot be accessed through traditional equilibrium points located in thexr-yrorbital plane. There are both allowed and forbidden zones in space to place a solar sail at AEPs,8depending on the direction of the thrust,52i.e. the direction of the vector n.In this research, the thrust generated by the solar sail is restricted to thexr-zrdirection in order to better analyze and show the results. According to Eq. (8),the solution forny=0 isyr=0, which means that only AEPs located on thexr-zrplane are chosen to observe Ida in this research. Hence, thenxandnzcomponents of the vector normal to the solar sail becomenx=cos γ andnz=sin γ,and the two nontrivial components left from Eq. (8) can be written as

For clarity purposes in the analysis of the results,a new set of coordinates is defined as［x，y，z］=［xr-R，yr，zr］.Note that the new coordinates can be seen as the position of the spacecraft with respect to Ida in the rotating frame of reference defined above. The values of the parameters used in this research are shown in Table 1. Using these values, Eqs. (9)and (10) are numerically solved forxandzas functions of the angle γ with an accuracy of the order of 10-13. They are shown in Figs. 2 and 3. These solutions represent artificial equilibrium points, which are a combined set of parameters and position so that the motion of the spacecraft is stationary in the rotating frame of reference.

2.4. Transfers between the AEPs near Ida

The parameters for the Sun-Ida system shown in Table 1 are taken into consideration.Thus,Eqs.(9)and(10)become functions of the position coordinatesxrandyrand the inclination of the solar sail γ. The AEPs which are solutions of Eqs. (9)and (10) are shown in Figs. 2(a) and (b) as functions of the position coordinatesxandzfor several values of the inclination γ. Note that each pair of solutionsx-zshown in red in Figs. 2(a) and (b) is related with a specific value for the inclination γ. Some of these values are also shown. The red lines in Figs.2(a)and(b)represent the AEPs close to the Lagrange pointsL1andL2, respectively. These points can be used to park a spacecraft to observe the asteroid 243 Ida from a stationary position above(or below)thex-yplane of this system.Some of the equilibrium points are highlighted in black next to their respective straight lines that represent the attitude of the planar solar sail, i.e. its inclination with respect to the solar rays coming from the left side. Note that there are several different locations to observe Ida, including the pole-sitter-like orbits. It is just a question of using the correct value of γ.The contours of the AEPs in thex-zplane shown in Figs. 2(a)and(b)are different from the ones well known in the literature as functions of the magnitudes of the thrusts (or the sail lightness number).8The difference is in the fact that the contours of Figs. 2(a) and (b) are shown as functions of the attitude of the sail, following a more recent work for the case of the Sun-Earth system,21but for the Sun-Ida system instead.

Since different perspectives are also good to observe several regions of Ida, some transfers will be made between some of the AEPs, like the ones marked by the pointsA, B, C, D,L1,andL2shown in these figures.The goal now is to simulate these transfers taken into account the solar radiation pressure over the spacecraft with the objective of finding the ones that consume as little fuel as possible. The fuel consumption of the transfers between the points is greatly affected by the solar radiation pressure,as shown in the results.We chose the pointsAandCdue to their privileged positions to observe Ida.Let an angle θ be defined as the angle between ridaand thexaxis.Among the AEPs on the red curve of Fig. 2(a) and (b) forx>0 andz>0, the pointAis approximately the one where this vector makes the highest angle θ with thexaxis(θA=47°),which means that it is a privileged point to observe Ida with different perspectives in comparison to points in thex-yplane. It can be seen in Fig. 3. The pointBis simply symmetrical toAforz<0. Analogous analyses were done to choose the pointC(and its symmetricalD), that is, among the red curves of Fig. 2(a) and (b), this point can best cover the pole-sitter-like orbits for Ida forz>0 or forz<0, in the case of pointD.

Table 1 Parameters of the Sun-Ida system [53,54].

In order to maintain consistency with the model to find the AEPs, the orbital maneuvers are also made using the threedimensional restricted three-body problem and are assumed to be a combination of bi-impulsive maneuvers, with the impulses applied at the initial and final points of the maneuver,and the continuous thrust given by the solar radiation pressure. This method was already used in several problems.43-49The main reason to find bi-impulsive transfers considering the solar radiation pressure is to make a more realistic study of orbital maneuvers that are based on the use of thrusters that act in the spacecraft for shorter time in an environment where the solar radiation pressure is important in the dynamics of the spacecraft. In locations where the gravity fields and other forces are weak, the thrusters do not need to be very high to be considered as ‘‘impulsive”. Their magnitudes depend on each particular case and the accuracy desired for the trajectories,so there is no general rules for that.The extra requirement of having an impulsive thruster in the spacecraft may be a problem in some missions, but not always, in particular considering the small magnitudes of the impulses. A spacecraft may require a thruster like that for other maneuvers to be realized during the trajectory from the Earth to the target bodies,and/or for the insertion in the asteroid system.In this way,the present paper makes the contribution of studying a combined‘‘solar radiation pressure + bi-impulsive maneuver” to show some important aspects of this idea,like the existence of transfers with minimum consumption of fuel, etc. It can be used in missions where it is practical from an engineering point of view.It is a topic that is not explored in the literature and that can offer useful solutions for some missions.

Fig. 2 AEP around Lagrange point L1 and L2.

Fig. 3 Angle θ.

The method of calculation is based on the ‘‘Lambert perturbed problem”,40,55where it is desired to find a trajectory in a force field that takes into account the gravity of the bodies and the solar radiation force and that passes by two given points in a given time.In that sense,the initial and final points for the transfer are given by the definition of the problem and the transfer time is varied.It makes this problem a Two-Point Boundary Value Problem (TPBVP) under a dynamics that gives no analytical solution. The numerical approach to solve this problem has the steps that are described below.

Step 1.Guess a first value for the initial velocity of the spacecraft at the initial point of the transfer so, together with its initial prescribed position,we have the complete initial state. This first guess is obtained from the solution of the Lambert problem,assuming a two-body dynamics with the asteroid as the central body.

Step 2.Specify a transfer time for the maneuver and integrate the equations of motion during this time.

Step 3.Verify the final position achieved by the spacecraft after the numerical integration and compare it with the prescribed final position.If there is an agreement,defined by a difference between the obtained and the prescribed positions less than a specified error, the solution is assumed to be found and the process can stop here. If there is no agreement, an increment in the initial velocity is made and the process goes back to Step 1.

There are many alternatives for the method to be used to find the increment in initial velocity, but we choose the standard gradient method, as described in Ref. 56. The main idea is to evaluate numerical derivatives of the final position of the spacecraft with respect to the initial velocity and use them to guide the search for the numerical solution.The routines available in this reference are also used here with minor modifications. More information can be seen in Ref. 57. The solution for such boundary value problem may not be unique for a given time of flight and families of paths may arise for a varying time of flight.58After finding this solution, the differences in the velocity of the spacecraft in the transfer orbit and in the given initial and final points are calculated. They represent both impulses of the bi-impulsive transfer. Then, by varying the transfer time, we can build families of solutions, from where we can find the ones with minimum increment of velocity required, as well as any other transfer desired, like given magnitude of impulses, given transfer time, etc. The results show that the natural force given by the solar radiation pressure can be used to reduce the fuel expenditure required by the bi-impulsive transfer by finding the proper time and geometry of the impulses.

The CRTBP is used in this work instead of the Hill model due to the fact that the trajectories of the transfers go outside the Hill’s sphere, whose radius is 9064 km.27The trajectories for transfers between the AEPAandBconsider paths that are up to 16000 km far from Ida. Transfers fromCtoDand fromL1toChave paths that are up to 20000 km from Ida.Transfers fromL2toAhave paths that are up to 12000 km from Ida. Thus, in order to keep the consistency with a more generalized problem (also valid for a spacecraft away from Ida),we preferred to use the CRTBP with solar radiation pressure instead of the Hill’s approximation.

The fuel consumed is specified by the total variation of the velocity Δvapplied to the spacecraft in both impulses.The necessary conditions used to simulate the transfers between these points are as follows:

(1) The initial and final coordinates of the transfer: (xi,0,zi)and (xf,0,zf), where (xi,0,zi) is the initial position of the spacecraft at the initial AEP and(xf,0,zf)is the final position of the spacecraft at the final AEP.

(2) The angle γ,that represents the attitude of the solar sail:(γi) in the initial point and (γf) in the final point.

(3) A given time T to transfer the spacecraft between these equilibrium points. In this work, the time T used to make the transfers ranges from 0 to 300 days,with intervals of 1 day.

(4) The light-catching surface of NanoSail-D2 is about 10 m2, while the mass of such spacecraft is about 4 kg.The area-to-mass ratio of such spacecraft is about 2.5 m2/kg. The Ikaros mission launched a spacecraft equipped with a solar sail whose area was about 180 m2. The initial total mass of the spacecraft was about 315 kg.Hence,the area-to-mass ratio of such spacecraft is about 0.6 m2/kg.17,59Although the area-to-mass ratio and other parameters like efficiency by reflectance of the spacecraft depend on the mission, in this work we have chosen an area-to-mass ratio fixed to be 0.3 m2/kg,which is compatible with actual technologies.

Table 2 shows the equilibrium positions in the （x，z） plane,and their respective γ for six points that are shown in Figs.2(a)and (b). These points are considered for the transfers in this work.

After solving this problem for each timeT,the velocities at the start and end of the maneuver are obtained. Those values are the magnitudes of the first and second impulse applied to the spacecraft, because they start and finish their transfer trajectories with velocity zero.

Table 2 Parameters for equilibrium points.

2.5. Solar sail configurations during the transfers near Ida

The vector n depends on the angle γ.In this work,it is assumed that the angle γ is constant or varies linearly in time.The most general case has a transfer according to the rule

where γiis the value of γ in the initial position of transfer phase(γi=γ（0）); α is a constant to be evaluated from α=（γf-γi）/T,whereTis the total transfer time and γf=γ(T)(the value of γ in the final position of the transfer phase).

Note that a reaction wheel with constant angular velocity can be used for the purpose of controlling the attitude of the spacecraft with a linear variation of γ.This assumption is made to give more control to the transfer, and at the same time,keeping a control law of the attitude of the solar sail that is not too complex to be implemented in the spacecraft. Besides complexity in implementation, variations of the attitude with more degrees of freedom would require more fuel consumption for the attitude maneuvers and introduce errors in the dynamics.In that sense,we limit this variation to linear.Note that,in the case where γi=γf,the angle γ（t）is assumed to be constant.This general case can be reduced to four different configurations for the solar sail in the present paper, according to Eq.(11):

Case 1.γ has a linear variation in time with constraints in γiand γf.In this configuration,the value for γiis given by γ of the initial equilibrium point for t=0(as shown in Table 2)and the value for γfis given by γ of the final equilibrium point for t=T (as shown in Table 2).

Case 2.γ has a linear variation in time with no constraints in γiand γf.In this configuration,the force due to the solar radiation pressure varies in time similarly to the previous configuration. However, the initial and final angles, γiand γf, have no restrictions. They are not fixed with the same values for the equilibrium points, as presented in Table 2.In this case, attitude maneuvers are made in the start and end of the transfer to meet the equilibrium conditions.

Case 3.γi=γf=0°→γ（t）=0°. In this configuration,according to Eq. (6), the force due to the solar radiation pressure is considered constant in its maximum value due to the term cos2γ=1, which means that, during the transfer, the vector normal to the solar sail and the solar rays make an angle of 0°.

Case 4.γi=γf=90°→γ（t）=90°

In this configuration,according to Eq.(6),the force due to the solar radiation pressure is zero due to the term cos2γ=0,which means that,during the transfer,the vector normal to the solar sail and the solar rays make an angle of 90°.

3. Results and discussion

First of all, analyses on AEP on thex-zplane are done for a general system in Subsection 3.1 in order to explore advantages of AEP for binary systems with very different masses,which is the case of a Sun-asteroid system. Thus, analyses of AEP and transfers between them will be done for the Sun-Ida system.Several families of transfer orbits between the equilibrium points are found as a result of the different configurations shown in Subsection 2.5, for several values of γi, γfand the total time of flight. In this section, we show the results for transfers between the points whose coordinates are given in Table 2:AtoB,CtoD,L1toC, andL2toA. The results for each transfer are presented in the next subsections.Remember that all the transfers are based on a bi-impulsive maneuver aided by the solar sail.

3.1. AEP on the x-z plane

The first investigation of the paper is the behavior of the artificial equilibrium points in thexr-zrplane around the LagrangianL1as function of the ratio massM1/M2. In order to accomplish the task, in this subsection, and only in it, an unit of length uL is defined such thatR=1uL,and an unit of time uT is defined such that μ1+μ2=1uL3/uT2.

The units ofkpdefined in Subsection2.2are uL3/uT2.Note that uL and uT depend on the system taken into consideration,i.e., on the ratio μr=μ1/μ2. On the other side, uL3/uT2is a constant for all systems. In the case where the area-to-mass ratio of the spacecraft isA/m=0.3 m2/kg, the value ofkpiskp=0.000461375.uL3/uT2for any value of the ratio μr.

We are investigating solutions in thexr-zrplane. Thus,yr=0 and the j component of n is null.In this case,the vector normal to the solar sail is n=［cos（γ）i，0，sin（γ）k］.The AEP on thexr-zrplane can be obtained by solving the two components left of Eq.(7).The AEP for all the values of γ from 0 to π/2 are shown in Fig. 4 for several different ratios of masses μr. This ratio for the Sun-Earth system is μr=3.28901×105, while for the Sun-Ida system is μr=4.82591×1013.

In the case where μr<1011, the equilibrium points path starts from the LagrangeanL1for γ=π/2,reaches some‘‘altitude”, i.e. increases itszrcomponent while decreasing thexrcomponent up to a maximum value forzrand then, decreases itszrcomponent while still decreasing thexrvalue.Finally,the path reaches thexraxis forzr=0 and γ=0. This pattern is changed for μr>1012. The equilibrium points start from the LagrangeanL1, whose coordinates are （xL1，0）, for γ=π/2 through a different path. Thexrvalues of the equilibrium points increase while they reach higher distances from the ecliptic plane of motion in thexr-zrplane. This different pattern means that, for μr>1012, the AEP may be located closer toM2and/or can be used as a better spot to observeM2that cannot be observed from the traditionalL1(the AEP may be aboveM2). The maximum angle θ for each set of equilibrium points (for each value of μr) shown in Fig. 4 is shown in Table 3.

Table 3 Maximum angle θ reached as function of mass ratio.

Fig. 4 AEP near xL1 for all the values of γ and for different values of mass ratio.

Fig. 5 AEP near L1 for the Sun-Ida system and for different values of γ.

The particular case of the Sun-Ida system(μr=4.82591×1013)is shown in Fig.5,in more suitable units.In comparison with the equilibrium pointA, the pointEis almost five times far from Ida. On the other side, the angle θ for the pointEis θE=81°, while this angle for the pointAis θA=47°. The pointEhas the highest value for θ for the Sun-Ida system. This point is better located over Ida and it can be used to observe the asteroid from ‘‘above” it with respect to the ecliptic plane. In the case where the asteroid rotates with low inclinations,this spot can be used to cover its poles.

3.2. Transfers from AEP a to b

The first transfer is between the two artificial equilibrium pointsAandBshown in Fig. 2(a) and (b). These AEPs have two main advantages: they are closer to the asteroid than the Lagrange pointL2and they are above/below thex-yplane.Thus, these points have special perspectives for pole-sitterlike orbits near Ida. During the transfer, the spacecraft is able to observe the asteroid from many different perspectives,moving from a positivezregion to a negative one and vice-versa,as shown in Fig. 6, which shows the trajectories projected in the(x-z)plane for different intervals of time of the transfers ranging from 1 to 300 days. The Cases 1, 2, 3, and 4 given in Subsection 2.5 are represented in Figs. 6(a) -(c), and (d),respectively. The paths of Fig. 6(a) look more ‘‘complicated”than the others shown in Figs. 6(b), (c), or (d). Thus, an analysis will be done for the trajectories of these figures.The paths that involve the shortest time are the ones with the shortest length. They are represented by the red dots. Such paths involve the highest Δvcosts. The paths get closer to Ida as the duration of the transfer is increased.We can note this continuity in the transition from the red to the green dots. Now,an analysis will be done in the green range of time (141 -208 days). The paths cross thex-yplane (z=0) in different behaviors (with discontinuities) for this range. They cross on the right side of Ida for lower time, but in the cases the time is increased, the paths transit to the other (left) side of Ida.Then,if the time is increased even more,the paths transit back again to the right side of Ida. Finally, for longer time, specifically in the blue range (more than 208 days), the paths cross thex-yplane on the right side of Ida.

The results found for this transfer are shown in Fig.7.The minimum Δvfound during the transfer as functions of different initial and final values of the angles (γiand γf) are shown in Fig. 7(a). The respective time of transfers for the minimum Δvare shown in Fig. 7(b). Note that the values of γ varies according to Eq. (11) in the range from -90° to 90°.

Fig. 6 Trajectories from A to B for Cases 1-4.

Fig. 7 Transfers from point A to B.

The best results with respect to the Δvcosts for this transfer are found in the top left of the plot of Fig.7(a),where the lowest values are found.It represents the region of minimum Δvin the order of 0.2 m/s, represented by the dark blue region. On the opposite side, the red regions around γifrom -45° to 90°and γffrom -90° to 45° represent the regions of larger fuel consumptions. These regions in red also represent the minimum time of flight, around 100 days, as can be seen if compared with Fig. 7(b), which shows that the longer transfer time is near γi=90°, in the order of 320 days, which in turn may also be useful for missions that require longer observation time.

The results for the four solar sail configurations described in Subsection 2.5 are shown in Fig. 7(c). Note that the minimum Δvare reached for a transfer time between 125 and 150 days, for most cases, as can be checked in Table 4.

Case 1 is shown by the red line, where γi=57.35°and γf=-57.35°, which are the values of γ that allows the spacecraft to remain in equilibrium at the pointsAandB, i.e. the spacecraft does not need to change its attitude before the travel and it arrives with the corresponding correct attitude to stay at the AEPB. Case 2 is represented by the green line, where γi=-76.71°and γf=76.71°the values of γ that resulted in the lowest fuel consumption. Although these values do not let the spacecraft to remain in equilibrium neither before nor after the transfer (attitude maneuvers are required before and after the transfer to place the spacecraft in equilibrium),the maneuver uses solar radiation pressure during the transfer to get very large savings in fuel, around 20% of the expenditures of the other simulations.Case 3 is shown by the blue line,where γi=0°and γf=0°,which means that, during the transfer, the vector normal to the solar sail and the solar rays will always make an angle of 0°, so maximizing the force applied over the spacecraft during the transfer. Case 4 is indicated by the red line,where γi=90°and γf=90°,which means that,during the transfer,the vector normal to the solar sail and the solar rays will always make an angle of 90°so minimizing the force applied over the spacecraft.Table 4 shows the lowest values of Δvfound for each solar sail configuration and the corresponding time required by the transfer. The discontinuities shown in Fig. 7(c) for the Cases 1-3 around the minimum Δvare due to a close approach to Ida during the transfer, as can be observed in the projection of the trajectories shown in Fig. 6. These discontinuities exist around the minimum Δv.

Table 4 Transfers from A to B.

Fig. 8 Trajectories from point C to D.

3.3. Transfers from AEP C to D

The transfers between the two artificial equilibrium pointsCandDshown in Fig. 2(a) and (b) are now studied. They are close to the Lagrange pointL1. The results found for these points are shown in Figs. 8 and 9. Trajectories for the Cases 1, 2, 3, and 4 given in Subsection 2.5 are represented in Figs. 8(a)-(d), respectively. Fig. 9(a) shows Δvas a function of γiand γf. In this transfer, the lowest values for the Δvcosts are found in the bottom left and in the top right of the plot of Fig. 9(a), in the order below 1 m/s, represented by the dark blue regions. On the opposite side, the red regions around-30°<γi<75°and -75°<γf<30 represent the regions of larger fuel consumptions. These regions in red also represent minimum time of flight, between 140 and 180 days. This can be seen by comparing Fig. 9(a) with Fig. 9(b). This last one shows that the longer transfer time is near γi≈-90°and γi≈90°in the order of almost 300 days. The results for the four solar sail configurations given in Subsection2.5are shown in Fig.9(c).Note that the minimum Δvare reached for a transfer time between 270 and 300 days, for Cases 2 and 4. Such minimums can also be checked in Table 5, where the lowest values of Δvare shown for each case. Optimizing the transfer using a linear attitude with free end points makes larger reductions in the fuel consumption during the transfer.Case 1 is represented by the blue line of Fig. 9(c), where γi=70.74°and γf=-70.74°The black line represents Case 2, where γi=90°and γf=65.84°the values of γ that result in the lowest fuel consumption. Case 3 (γ=0°is represented by the green line.The purple line represents Case 4 (γ=90°).

3.4. Transfers from L1 to AEP C

The transfers are now between the Lagrange pointL1and the artificial equilibrium pointCshown in Figs. 2(a) and (b). The spacecraft will be moved fromz=0 to a positivezregion.However,in this transfer,Δvis smaller than the one necessary to move the spacecraft fromCtoD. The results found for these points are presented in Figs. 10 and 11. The best results with respect to the Δvcosts for this transfer are found in the bottom left and top right of the plot of Fig. 11(a), where the lowest values are found. It represents the region of minimum Δvas a function of γiand γf, in the order of 0.5 m/s, represented by the blue regions. The red and orange regions represent the larger fuel consumptions,as well as the minimum time of flight, around 100 days, as can be seen by comparing with the results of Fig. 11(b). A particular region of low fuel consumption and long transfer time can be seen for a low rate of change of γ during the transfer,for γ near±90°.The results for the four solar sail configurations given in Subsection2.5are shown in Fig. 11(c). The minimum Δvare reached for a transfer time between 240 and 300 days, for most cases, as can be checked in Table 6. Case 1 is shown by the red line,where γi=90°and γf=70.74°while Case 2 is indicated by the green line, where γi=59.79°and γf=90°Table 6 shows the lowest values of Δvfound for each solar sail configuration and the corresponding time required by the transfer.As usual,very large savings in Δvare obtained by optimizing the maneuvers.

Fig. 9 Transfers from point C to D.

Table 5 Transfers from C to D.

3.5. Transfers from L2 to AEP A

This transfer is now between the Lagrange pointL2and the artificial equilibrium pointAshown in Figs. 2(a) and (b).The trajectories for the transfer between these points are shown in Fig. 12, while the Δvcosts involved are shown in Fig. 13. The larger values for Δvare in red in Fig. 13(a), from 1.2 to 2 m/s. It represents minimum time of flight, around 100 days, as can be seen when comparing it with Fig. 13(b).On the other side, the best results with respect to the Δvcosts for this transfer are found in the top right of the plot of Fig.13(a)in the order of 0.8 m/s,represented by the dark blue region.This same region is represented in red in Fig. 13(b). The minimum Δvare reached for a transfer time between 200 and 250 days,for most cases.This can be checked in Table 7,which shows the lowest values of Δvfound for each solar sail configuration and the corresponding time required by the transfer.The results for the four solar sail configurations given in Subsection2.5are shown in Fig.13(c).Case 1 is represented by the red line,where γi=90°and γf=57.35°.Case 2 is shown by the green line, where γi=71.88°and γf=71.88°(the value of γ that results in the lowest fuel consumption).Case 3 can be seen in the blue line.Case 4 is shown by the purple line. In this situation,Case 2 does not give very large savings when compared with the maneuver shown in Case 1. The advantage of Case 1 is that the spacecraft departs and arrives at the equilibrium points with the correct attitude. The advantage of Case 2 is that attitude maneuvers are not required during the travel(γi=γf). Thus, either option could be chosen, depending on the type of spacecraft and mission. Both options provide fuel savings in comparison with Cases 3 and 4,as shown in Table 7.

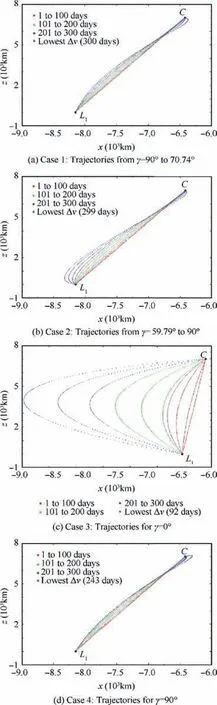
Fig. 10 Trajectories for L1 to C.

Table 6 Transfers from L1 to C.

Fig. 12 Trajectories from point L2 to A.

4. Conclusions

The artificial equilibrium points allow a spacecraft to park closer to the body, so improving the quality of the data coming from the mission. It is also possible to find points that are out of the plane of the primaries, so allowing polesitter-like orbits for privileged observation perspectives of the asteroid. This is very important, because it gives the whole picture of the surface of the celestial body, since the asteroid rotates. In this work, we compute the AEPs considering a spacecraft equipped with a solar sail in orbit in the Sun-Ida system. Besides finding these new points, maneuvers to transfer the spacecraft between them are also made. In particular, the present paper focuses on transfers that use a bi-impulsive control, which is a simple and usual technique to maneuver a spacecraft, but that includes the effect of a solar sail during the transfer to help to minimize the costs of the transfer. Several different forms are studied to make a bi-impulsive transfer between AEPs, using different configurations of the solar sail during the trip, by varying its attitude. The results show that it is possible to make these transfers between the new equilibrium points to consume less fuel, which can improve the duration of the mission and even make new maneuvers around the target body. On the other hand, the results also show that transfers with longer duration are also an option. These possibilities offer a large range of locations for the spacecraft, which give more applications to a mission.

Fig. 13 Transfers from point L2 to A.

Table 7 Transfers from L2 to A.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The authors acknowledge financial support from CAPES -Coordination for the Improvement of Higher Education Personnel;from CEFET-MG-Federal Center for Technological Education of Minas Gerais; from CNPQ - National Council for Scientific and Technological Development (Nos.406841/2016-0 and 301338/2016-7); from FAPESP - Sa˜o Paulo Research Foundation (Nos. 2016/24561-0, 2019/18480-5, and 2018/07377-6).