Time-domain nonlinear aeroelastic analysis and wind tunnel test of a flexible wing using strain-based beam formulation
Yang MENG, Zhiqiang WAN, Changchuan XIE, Chao AN
School of Aeronautic Science and Engineering, Beihang University, Beijing 100083, China
KEYWORDS Flexible wings;Flutter;Geometric nonlinearity;Gust response;Wind tunnel test
Abstract A theoretical formulation for time-domain nonlinear aeroelastic analysis of a flexible wing model is presented and validated by wind tunnel tests.A strain-based beam model for nonlinear structural analysis is combined with the Unsteady Vortex Lattice Method(UVLM)to form the complete framework for aeroelastic analysis.The nonlinear second-order differential equations are solved by an implicit time integration scheme that incorporates a Newton-Raphson sub-iteration technique. An advanced fiber optic sensing technique is firstly used in a wind tunnel for measuring large structural deformations.In the theoretical study,the nonlinear flutter boundary is determined by analyzing the transient response about the nonlinear static equilibrium with a series of flow velocities.The gust responses of the wing model at various gust frequencies are also studied.Comparisons of the theoretical and experimental results show that the proposed method is suitable for determining the nonlinear flutter boundary and simulating the gust response of flexible wings in the time domain.
1. Introduction
In recent years, High-Altitude Long-Endurance (HALE)Unmanned Aerial Vehicles (UAVs) have attracted lots of attention. Featured by the lightweight design and high aspect ratio, wings of this kind of aircraft are flexible and produce large deformations in flight. The large deformation may lead to significant changes in structural dynamics and aeroelastic characteristics of the aircraft. Many of the previous studies1-10have highlighted the effects of geometric nonlinearity caused by the large deformation on dynamic stability, Limit Cycle Oscillation(LCO)and flight dynamics.It has been proved that the linear theory fails to model the large deformation and reflect the resulting effects accurately. In the early 1990s, van Schoor and von Flotow1first studied on a typical flexible aircraft to investigate the uncommon aeroelastic characteristics.They concluded that the aircraft dynamics highly depends on the flight conditions. However, the method is linear and the geometric nonlinearity due to large deformation was not considered.Patil and Hodges3,4firstly took the structural geometric nonlinearities into an aeroelastic analysis.They developed a fully-coupled formulation that uses a mixed variational formulation for nonlinear structural analysis and finite-state inflow theory for unsteady aerodynamics to investigate the effects of structural flexibility on trim analysis and flight dynamics.Besides, the static or dynamic structural deformation caused by gusty environment or maneuver may lead to excessive loading or even failure, as learned from the mishap of NASA’s Helios.11Thus, an appropriate nonlinear aeroelastic formulation must reflect and accurately model the geometric nonlinearities in both structural and aerodynamic aspects.
As suggested in NASA’s report,11it is necessary to ‘‘develop more advanced, multidisciplinary time-domain analysis methods appropriate to highly flexible, morphing vehicles”.Full-scale CFD/CSD coupling computations of the complete aircraft are not suitable for aircraft design in preliminary stage,optimization and control law design. It is desirable to develop a high-fidelity and low-order model for nonlinear aeroelastic analysis.A recent review written by Xiang et al.12summarized the research techniques in dealing with nonlinear aeroelastic problems. They emphasized the significance of high computational efficient methods and three-dimensional effects in both structural and aerodynamic models. Liu et al.9combined structural nonlinear Finite Element Method (FEM) with the steady Vortex Lattice Method (VLM) to simulate the static deformation of a flexible wing in given conditions and validated the theoretical results by a wind tunnel test.By introducing unsteady effects, they further studied the nonlinear flutter and gust response of a high-aspect-ratio wing and compared the theoretical results with the wind tunnel test.13In the most recent research, Liu and Xie14established a unified theoretical framework for aeroservoelastic stability analysis and highlighted the necessity to consider the geometric nonlinearities when dealing with aeroservoelastic problems. To further reduce the structural order and increase the computational efficiency, modal approaches have been used for solving geometrically nonlinear problems in which the approximate displacements are expressed by several linear modes and high-order modes.15-18Even though the geometric nonlinearities are properly captured, the main disadvantages of this method root in that the approximation needs to be determined by prior computations of nonlinear static deformations.
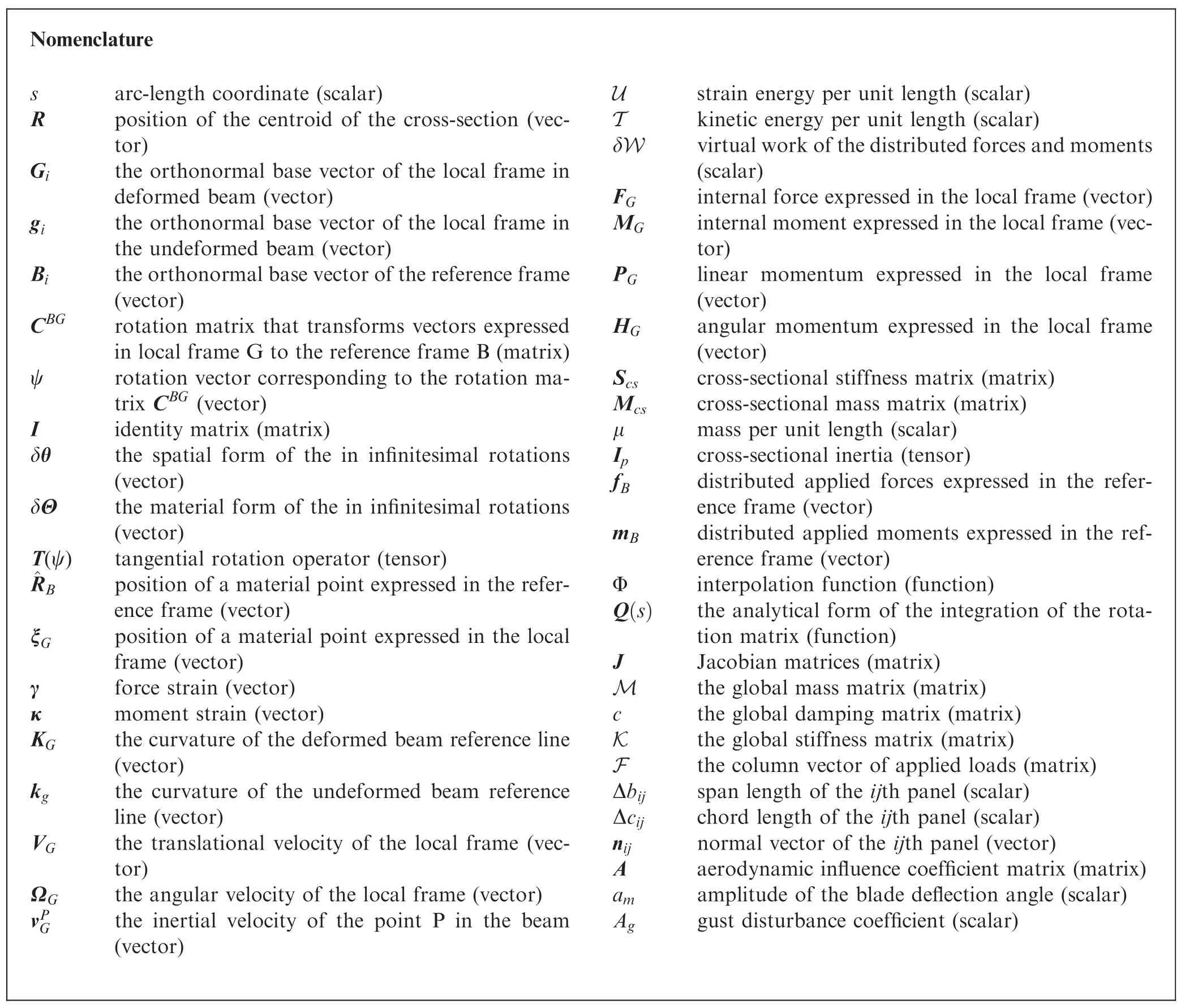
Nomenclature sarc-length coordinate (scalar)Rposition of the centroid of the cross-section (vector)Githe orthonormal base vector of the local frame in deformed beam (vector)githe orthonormal base vector of the local frame in the undeformed beam (vector)Bithe orthonormal base vector of the reference frame(vector)CBGrotation matrix that transforms vectors expressed in local frame G to the reference frame B (matrix)ψrotation vector corresponding to the rotation matrix CBG (vector)Iidentity matrix (matrix)δθthe spatial form of the in infinitesimal rotations(vector)δΘthe material form of the in infinitesimal rotations(vector)T(ψ)tangential rotation operator (tensor)^RBposition of a material point expressed in the reference frame (vector)ξGposition of a material point expressed in the local frame (vector)γforce strain (vector)κmoment strain (vector)KGthe curvature of the deformed beam reference line(vector)kgthe curvature of the undeformed beam reference line (vector)VGthe translational velocity of the local frame (vector)ΩGthe angular velocity of the local frame (vector)vPGthe inertial velocity of the point P in the beam(vector)Ustrain energy per unit length (scalar)Tkinetic energy per unit length (scalar)δWvirtual work of the distributed forces and moments(scalar)FGinternal force expressed in the local frame(vector)MGinternal moment expressed in the local frame(vector)PGlinear momentum expressed in the local frame(vector)HGangular momentum expressed in the local frame(vector)Scscross-sectional stiffness matrix (matrix)Mcscross-sectional mass matrix (matrix)μmass per unit length (scalar)Ipcross-sectional inertia (tensor)fBdistributed applied forces expressed in the reference frame (vector)mBdistributed applied moments expressed in the reference frame (vector)Φinterpolation function (function)Q(s)the analytical form of the integration of the rotation matrix (function)JJacobian matrices (matrix)Mthe global mass matrix (matrix)cthe global damping matrix (matrix)Kthe global stiffness matrix (matrix)Fthe column vector of applied loads (matrix)Δbijspan length of the ijth panel (scalar)Δcijchord length of the ijth panel (scalar)nijnormal vector of the ijth panel (vector)Aaerodynamic influence coefficient matrix (matrix)amamplitude of the blade deflection angle (scalar)Aggust disturbance coefficient (scalar)
By taking advantage of the slenderness, flexible wings can usually be modelled as beams. Patil19simulated the gust response of flexible aircraft by coupling the intrinsic beam formulation with two-dimensional (2-D) airfoil model. In Tang’s research,20responses of a suspended wing model in a gusty environment were studied by combined Hodges-Dowell equations for dynamics of beams with the 2-D ONERA model.The theoretical results show good quantitative agreement with those in the experiment. By the similar method to that used by Patil,19Zhang and Xiang21further studied the occurrence and sustaining mechanism of the LCO. Different from the displacement-based method or the mixed variational formulation,Cesnik and his co-workers6,22-25developed a strain-based beam model and the corresponding modal approach to model the flexible wings.The unsteady aerodynamic loads were calculated by the 2-D finite-state inflow theory. The main advantages of the strain-based formulation consist of two aspects:the inverse of a constant stiffness matrix for static problems and fast convergence rates for dynamic problems. Su and Song26further developed a real-time simulation platform for nonlinear aeroelastic analysis of flexible wings.These formulations, however, do not account for three-dimensional flow effect. The accuracy of the above 2-D airfoil models, such as the ONERA model and finite-state inflow theory, depends on some empirical parameters. Wang and Chen27,28replaced the two-dimensional airfoil model3by three-dimensional UVLM for nonlinear gust response analysis. Palacios et al.7further investigated the numerical efficiency and the significance of three-dimensional flow effect on flexible wings with large deformation. Although the 2-D unsteady airfoil loads can match a wide range of the expected motions of the flexible aircraft, they may lose accuracy for low-frequency and largeamplitude wing dynamics. Besides, the three-dimensional tip effects,which cannot be taken account for in 2-D aerodynamic models, can have effectively influence at low frequencies.
This paper presents a nonlinear aeroelastic analysis by coupling the nonlinear, geometrically exact, strain-based beam model with the UVLM. Different from the derivation of strain-based beam formulation in Ref. 24, the proposed beam formulation follows from the basic principles presented by Hodges29and the analytical relations between the moment strains and the rotation matrix. According to kinematic relations of the geometrically exact beam, the derivative of the rotations with respect to a certain parameter (e.g. arc length coordinate) equals the product of a rotation matrix and the skew-symmetric matrix of the derivative of the moment strains with respect to the same parameter. The resultant differential equations cannot be integrated directly in an analytical form.The key to obtaining the analytical solution of rotations based on the moment strains is to assume constant strains in the element. Finally, all the variables including velocity, angular velocity, displacement and rotations can be expressed by strains. UVLM is then used for calculations of the unsteady aerodynamic loads and coupled with the nonlinear beam model for time-domain simulations. The nonlinear secondorder differential equations are solved by an implicit time integration scheme that incorporates a Newton-Raphson subiteration technique.To validate the theoretical analysis,a flexible wing model is deliberately designed and tested in a wind tunnel with a gusty environment.Advanced fiber optic sensing system is implemented for measuring large structural deformations.Comparisons of the theoretical and experimental results show that the proposed theoretical method is effective and has reasonable accuracy in solving nonlinear aeroelastic problems.
2. Theoretical formulations
2.1. Structural dynamic modelling
2.1.1. Finite rotations and kinematics
As shown in Fig. 1, for a given arc-length parameters∈[0,L]⊂R, the deformed beam is defined by the combination of a beam reference line and cross-sections connected by the beam reference line,. The vector R(s,t) denotes the spatial position of the beam reference line.The orthonormal base vectors {Gi(s,t)}i=1,2,3define the local coordinate system attached to the cross-sections.G2(s,t)and G3(s,t)are two orthonormal unit vectors in the cross-section,G1(s,t)is perpendicular to the cross-sectional planes.It is noted that G1is not necessarily tangent to the beam reference line.For convenience,what follows the local bases of the initial undeformed configuration are denoted as {gi(s)}i=1,2,3. It is obvious that gi(s)=Gi(s,0).
A cantilevered wing is taken as the object in this study.It is convenient to introduce three fixed orthonormal base vectors,{βi}i=1,2,3,to define a fixed reference inertial coordinate system.The rotation matrix CBGrepresents the relationship between the local and the reference frames as well as the coordinate transformation between the components of the two representations.

Here,subscripts B and G indicate the corresponding frame in which the vector is projected.Meanwhile,one can define the rotation vector, ψ according to the Euler’s rotation theorem and express the rotation matrix CBGby the rotation vector ψ 30:

in which I is the identity matrix,and ψ=||ψ||is the 2-norm of the rotation vector. The skew-symmetric matrix,, is

The variation of the rotation matrix is shown as

Fig. 1 Kinematic description of a three-dimensional beam.

where δθ and δΘ are the infinitesimal rotations in spatial and material form, respectively. They can be related by

By making use of Eq. (2), the infinitesimal rotations are given by
in which T(ψ) is called the tangential rotation operator31and
Following the kinematic description by Hodges,29the position vector of a material point in the beam,,has the following explicit form:
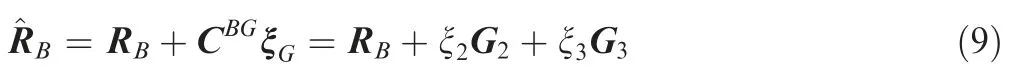
where ξG= [0 ξ2ξ3]Tdenotes the coordinate components expressed in the local frame,G. In present work, the warping effect is ignored and ξ2,ξ3keep constant. The relations between the variations of kinematic and strain variables are expressed as32

where γ and κ denote the force strain and the moment strain,respectively. The operator (°)′denotes the derivative ofs.These virtual relations can be easily integrated to obtain the following strain-configuration relations:

where KG, kgare the curvature of the deformed beam and the undeformed beam, respectively. The vector e1equals[1 0 0]T. Following Eqs. (5) and (7), the curvature vector KGis expressed by the spatial variation of the rotation matrix CBG:

Similarly, the inertial velocities of the material point P in the beam,, can be obtained by the time derivative of the position vector, ^RB, and expressed as

where VGis the translational velocity of the local frame and ΩGis the angular velocity of the local frame. They can be expressed as

2.1.2. Dynamic equations of motions (EOM)
From Hamilton’s principle, the variational formulation is derived as

in whicht1andt2are two arbitrary fixed time,Lis the beam length, T is the kinetic energy per unit length, U is the strain energy per unit length and δW is the virtual work of the applied load per unit length. According to Hodges,29the variations of internal and kinetic energies per unit length are

where the internal force FG, the internal moment MG, the linear momentum PGand the angular momentum HGare the derivative of the energies per unit length as follows:

where f is the distributed force and m is the distributed moment. Subscripts indicate the corresponding coordinate system.
Using the relations in Eqs.(17)-(22),the variational formulation in Eq. (16) becomes
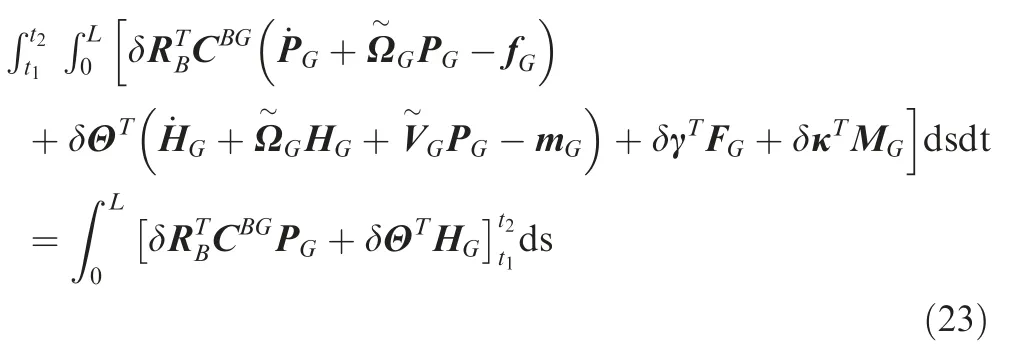
2.1.3. Constant-strain element
To solve the governing EOM Eq.(23),displacements and rotations are often chosen to be the primary interpolated variables.35By contrast, there is no restriction in additive-type interpolation by taking strains as the interpolated variables.Besides, the objectivity of the interpolation of finite rotations will not be an issue in a strain-based formulation. In present work, the strains are assumed constant within an element resulting in analytical expressions of the displacements and rotations by the interpolated strains.
By using the interpolation functions Φ(s), the force and moment strains can be approximated by discretized strains within the element:

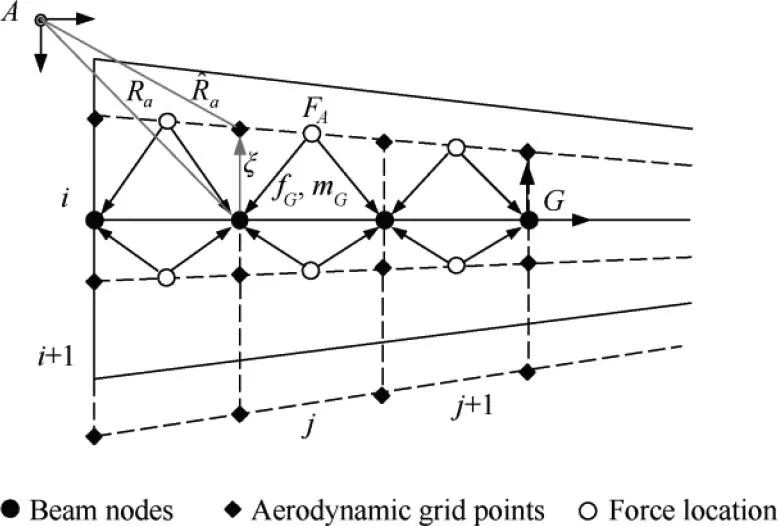
γiand κiare the constant strains with the segmentSi-1≤S Using the analytical relationships expressed in Eqs. (26)and (28), the variations of RBand Θ in Eq. (23) can be obtained. Before deriving these variations, variations of CBG(s) and Q(s) are prepared. By taking variation of Eq. (26), one obtains The variation in the second term is given by the definition of the directional derivative: where the scalar coefficients αiand βiare given by Note that δCBGand δare both third-order tensor. By multiplying δCBGby an arbitrary vector u, the variation δκ is extracted according to the rules of the vector product and we have where AC(s;κi,u)is independent of the unknown variables and can be given by whereAQ(s;κ,u) is independent of the unknown variables and can be given in a closed form: The variation of the derivative of the infinitesimal rotation δθ is given by Eq. (10): By integrating Eq.(41)with respect tosand using Eq.(29),one obtains Making use of Eq. (7), one can obtain the variation of the rotation vector ψ: where δRB0is corresponding to the boundary conditions. Substituting (39) into (44), the variation of RBcan be written as Eqs.(42)and(45)present a recursive procedure to calculate the infinitesimal rotation and the variation of the position vector within theith element. Without loss of generality, the reference frame is often chosen to be the local frame ats=0.Thus, we have relations=I and RB0=0. Finally, one can obtain where the barred vectors denote the column vectors consisting of all the discretized variables including positions, rotations and strains. The sub-matrices of the Jacobian matrices in the above equation are easily deduced from the prepared variations and expressed as follows: wherejrepresent nodal numbers corresponding to the nodal vectors RB(j-1),θj-1,ψj-1withj=1,2,...,n+1,andirepresent element numbers corresponding to the element strain vectors γiand κiwithi=1,2,...,n. Similar expressions for the temporal derivatives of the position and orientation vectors can be obtained as 2.1.4. Discrete form of EOM For simplicity, the beam reference line is assumed to go through the cross-sectional mass centers,i.e.=0.Substituting Eqs.(13),(14)and(19)into the governing Eq.(23),the following expression can be obtained: The inertia properties and the distributed loads are assumed to change linearly within an element. Using the relations in Eqs. (46) and (48), the discrete form of the EOM is written as In static analysis,the time-dependent terms in the resultant nonlinear second-order differential equations are omitted. A direct advantage of this formulation in dealing with static problems is the constant stiffness matrix. For nonlinear transient problems, the resulting equations will be solved using the implicit Newmark integration scheme incorporating Newton-Raphson iterations for solving nonlinear equations.36The basic idea is to firstly provide the predictions of the state variables and their time derivatives at each time step and employ a Newton-Raphson sub-iteration technique to correct the predictions. The unsteady aerodynamic loads are calculated by the UVLM and combined with the strain-based beam model for nonlinear aeroelastic analysis. Fig. 2 shows the lifting surface represented by a certain number of vortex ring elements covering both the wing surface and the wake. The leading segment is located at the quarterchord line. The no-penetration boundary condition is satisfied at the collocation point, which is placed on the center of the 3/4 chord line.The lifting-surface coordinate system is denoted asA. The x-axis is in the direction of the coming flow. The yaxis points to the right side of the wing. The z-axis is determined by the right-hand rule.All the variables discussed below are expressed in this coordinate system.U(t),V(t),W(t)represent the components of the flow velocity projected in the aerodynamic coordinate system. Γij,nij, Δbij, Δcijrepresent the vortex strength, normal vector, span length, chord length of theijth lattice, respectively. The counterivaries from 1 toMalong the chordwise direction and the counterjhas values between 1 and N along the spanwise direction. With the no-penetration boundary condition, the normal flow velocity across the thin wing’s surface must be zero and we have in which Φ denotes the full potential function,v represents the velocity of movement at the collocation point,and n represents the normal vector of the bound vortex lattice. Eq. (51) is further expressed as37 in which A is the aerodynamic influence coefficient matrix,which is obtained via Biot-Savart law, Γ represents the vortex circulation,V(t) is the velocity due to the wing’s motion or unsteady coming flow including the gust excitation and Vwis the velocity induced by the wake vortices. In this work, the fixed-wake model is used in the time-domain analysis, as shown in Fig.3.It can improve the computing efficiency compared to the free-wake model and provide satisfying accuracy in the response analysis. As the product[V(t)+Vw]·n is known,the right-hand side(RHS) of Eq. (52) at each time step is given by After determining the aerodynamic influence coefficient matrix, the following algebraic equations are obtained based on the boundary condition at each collocation point: whereKis the counter of collocation points vertically,Lis the counter of vortex rings horizontally andmequalsM×N. By solving the algebraic equations above and using the Bernoulli equation, the pressure difference on theijth bound vortex is obtained: where τiand τjrepresent the tangential vectors of theijth lattice. By setting a steady flow and keeping the lifting surface stable, the UVLM can be easily extended to calculate the steady aerodynamic loads. Fig. 2 Description of UVLM model. Fig. 3 Fixed wake model. As the beam model for nonlinear structural analysis is a space curve and the aerodynamic grid for aerodynamics calculation is surface in space, a mapping procedure between these two kinds of meshes is needed for aeroelastic analysis. Firstly,a mapping relationship between the nodal displacements and velocities of the beam and those of the grid points is developed. The positions of aerodynamic grid points in the aerodynamic frame can be expressed by the positions of the beam nodes and the local distance vector from the relevant node to the grid point, as illustrated in Fig. 4. In this paper,the spanwise aerodynamic mesh coincides with the finiteelement discretization of the beam. With the assumption of rigid cross-sections, the distance vector, ξ, remains constant when the beam deforms.Finally,the position ^Rand the velocityof the aerodynamic grid points, both expressed in theAframe, are given by Secondly, the aerodynamic forces are transformed to the forces and moments acting on the beam by maintaining the equivalent resultant force and resultant moment within a beam element. The total force is evenly distributed to two adjacent nodes. The nodal forces and moments acting on theJth node are Fig. 4 Mapping relationship between aerodynamic mesh and beam discretization. The static equilibrium serves for the initial condition in both gust response and nonlinear flutter analysis. The static aeroelastic characteristics are investigated prior to the timedomain dynamic analysis. A loosely-coupled strategy is applied to solve the static aeroelastic problem. The mapping relations defined in Eq. (56) are used to update the lifting surface according to the structural deformations before each computation of steady aerodynamic loads. Then, the calculated aerodynamics are applied to the beam nodes in the manner of Eqs.(57) and (58). The nonlinear static structural deformations and aerodynamic load distributions can be obtained after several iterative computations.Based on the static equilibrium state, the time-domain analysis is implemented by a looselycoupled scheme in which structural information and aerodynamic forces are exchanged at each time step. Specifically,the aerodynamic loads are firstly computed by UVLM and transformed to nodal forces and moments at the beginning of time stepn. The implicit Newmark scheme with a Newton-Raphson sub-iteration technique is introduced to solve the nonlinear second-order differential equations and calculate the nodal positions and velocities at then+1th time step. The system matrices including the mass matrix, the stiffness matrix and the damping matrix as well as the unsteady load are kept unchanged within a time step. This assumption will make sense with an appropriate time step. The procedure for the time-domain analysis is shown in Fig. 5. Taking the static equilibrium state as the initial condition,one can determine the values of concerned variables at each time step with various gust inputs. If the gust excitation is replaced by a linear dynamic perturbation such as a small velocity disturbance, the nonlinear flutter boundary can be obtained from the time history or phase-plane plots of the resulting responses. To validate the proposed strain-based beam model and the complete framework for nonlinear aeroelastic analysis, a wing model is designed and manufactured for wind tunnel tests. Fig. 5 Flowchart of nonlinear aeroelastic analysis in time domain. The wing model is deliberately designed to produce large deformation and notable features of geometric nonlinearity within the working range of the wind tunnel. Parameters of the wing model are listed in Table 1. The wing stiffness is mainly supplied by a rectangular steel ruler, which is located at the half chord line. The width and height of the beam cross-section are 35 mm and 1.5 mm, respectively. The material density is 7.75×103kg/m3, and the elastic modulus is 210 GPa. The wing shape is maintained by wooden wing ribs and plastic heat shrinkage film. The wing was divided into eight sections,each of which attaches to the steel ruler by a single point. 3 mm gaps were left between the adjacent sections for reducing the effect of the additional stiffness.An aluminum bar,which is 200 mm in length and 62 g in weight,is mounted on the wingtip to regulate the structural dynamic characteristics leading to a desirable flutter speed. Figs. 6 and 7 show the sketch and the test model for the wind tunnel test,respectively. Table 2 listed the first five natural modes of the wing model with a fixed root. The results are obtained from the strainbased formulation and solved in MSC. Nastran shows good agreements with the modal test results. The natural frequency of the first bending mode is quite low,indicating high flexibility of the wing. Measuring structural deformations, especially large deformations, is usually a big challenge during wind tunnel tests for aeroelastic purpose.In Ref.13,a camera measurement system is used to capture the structural displacements. However, it is found that the spanwise deflections will go beyond the marked range when the vertical deflections are quite large. In this paper, an advanced fiber optic sensing system is introduced to measure the structural deformation in an indirect way.Fiber Bragg Grating(FBG)sensors with different characteristic wavelength (called Bragg wavelength) are attached to the surface of the wing beam using epoxy adhesive, as shown in Fig. 8. TheX, Y, Zaxes are defined as spanwise, chordwise,and vertical directions, respectively. The FBG sensors are attached to different locations so that strain values at these locations can be obtained. Rotations and displacements of the wing beam along the wing span can be calculated by numerical integration of the measured strains with the Strain-Displacement Transformation (SDT) algorithm.38,39 As shown in Fig. 9, A 3-axis digital accelerometer(ADXL345)is located at approximately two-thirds of the span from the wing root to measure the vertical and chordwise acceleration. Table 1 Parameters of wing model. Fig. 6 Sketch of flexible wing model. Fig. 7 Wind tunnel test of wing model. Fig. 8 Installation of FBG sensor and accelerometer. Table 2 First five natural modes and frequencies (in Hz) of wing model. Wind tunnel tests, including static aeroelastic test, gust response test and flutter test, were all performed in a 3 m×3 m low-speed wind tunnel.As shown in Fig.10,the wing model is fixed to a suspension system vertically. The suspension system is designed rigid compared to the flexible wing model.The wing root can be rotated from a 0°Angle of Attack(AOA)to 5°AOA taking the undeformed wing as reference.A six-component balance was set at the wing root to measure the forces and moments. Fig. 9 Relative locations of FBG sensors attaching to structure surface. As shown in Fig. 11, a gust generator is installed in the wind tunnel to create the expected gust condition in gust response test.The distance between the wind model and the gust generator is 2000 mm.The gust generator consists of an iron frame,two rectangular blades and a servo motor which links to the blades by a planar link mechanism. There is no difference between these two blades, each of which has the chord length of 300 mm, and the span of 2000 mm. Distance between these two blades is 600 mm. The airfoil is NACA0015. Each of the blades can deflect with a range from-7°to+7°.With continuous sinusoidal signals given to the servo motor, an approximately sinusoidal lateral gust is generated, and the gust velocity can be expressed as whereamrepresents the amplitude of the deflection angle andAgrepresents the gust disturbance coefficient, which depends on the wind speedVand the gust frequencyf. Fig. 10 Wing model installation in wind tunnel. Fig. 11 Gust generator in wind tunnel. Before the aeroelastic analysis, geometrically nonlinear static solutions and transient responses of a cantilever beam model and the wing model are firstly studied and compared to those calculated by the static solver in MSC.Nastran. 4.1.1. Nonlinear static solutions Fig. 12 shows a slender cantilever isotropic beam subjected to a concentrated tip load. The axial and lateral components of the tip force are zero, and the vertical component isFz. The properties of the cantilever beam are the same as those of the rectangular steel ruler described in Section 3.1. The beam is discretized into 25 elements in both strain-based formulation and MSC.Nastran. Fig. 13 shows the vertical and axial tip displacements with respect to varying tip force from 0 to 3(N). The results show very good agreement with those calculated by Nastran. As mentioned before, the stiffness matrix keeps constant and needs only one-time inverse computation in the proposed formulation. By contrast, the inverse computation is required at each iteration due to the updated stiffness matrix in the displacement-based method. This makes the strain-based formulation more efficient in dealing with geometrically nonlinear static problems. The same tip forces are also applied to the wing model described in Section 3.1. The vertical and axial tip displacements with respect to tip loads are plotted in Fig. 14. The results calculated by strain-based formulation show good agreement with those solved in Nastran. 4.1.2. Transient response The same cantilever beam model as in the static case is used for the transient response. A sinusoidal vertical force instead of the static force is given by Fig. 12 Cantilever beam subjected to tip loads. Fig. 15 plots the responses of the tip displacements calculated by the strain-based method and the dynamic solver in MSC.Nastran (SOL 400). The time steps in the strain-based method and Nastran are both set as 0.002 s. Here,UxandUzrepresent the axial displacement and vertical displacement,respectively.Excellent agreements can be observed between the two sets of results. Fig. 16 shows the responses of the tip displacements of the wing model under the same sinusoidal vertical forces. The results further demonstrate the accuracy of the presented strain-based method in solving dynamic problems. Fig. 13 Tip displacements with different tip forces (cantilever beam model). Fig.15 Tip displacements of cantilever beam under dynamic tip loads. Fig. 16 Tip displacements of wing model under dynamic tip loads. As previous studies show,2the nonlinear flutter boundary depends on the flight condition and can be determined by a linear dynamic perturbation analysis about the nonlinear static equilibrium. This study will determine the nonlinear flutter boundary by analyzing the transient response about the nonlinear static deformation with a series of flow velocities. The linear flutter results are obtained from MSC.Nastran (SOL 145) prior to the nonlinear flutter analysis. The first five natural modes are used for linear flutter analysis. The linear flutter speed is independent of structural deformation and loading conditions.As theV-gandV-fcurves plotted in Fig.17 show,the critical flutter speedVFis 31 m/s and the flutter frequency is 14.2 Hz.The result exhibits a typical twist/bending coupling flutter. Fig. 17 Linear flutter analysis results. Fig.18 Wingtip displacements with varying flow velocities from 10 m/s to 18 m/s. Fig. 19 Displacements along wing span for α=3° and V=18 m/s. Fig. 20 Bending curvatures about Y axis along wing span for α=3° and V=18 m/s. To investigate the characteristics of nonlinear flutter, the wing was suspended vertically under the 3° AOA. Fig. 18 presents the linear results calculated by Nastran, the nonlinear results by the presented method and the test results of wingtip displacements with varying flow velocities from 10 m/s to 18 m/s. The displacements obtained from the strain-based method, which includes the geometrically nonlinear effect,show good agreement with those measured in the wind tunnel test.However,the linear static aeroelastic solutions in Nastran(SOL 144) exhibit large differences from both the nonlinear results and test results. The linear results are bigger than the other two sets of results, and the differences increase with velocity growing up.It shows that the linear theory fails to predict the structural deformation for geometrically nonlinear problems accurately.Fig.19 shows the deformed configuration of the wing at a certain state (V=18 m/s, α=3°). The maximum tip displacement is approximate 20% of the wing span.The large deformation can result in significant changes in dynamic characteristics. Test results obtained by fiber optic sensing technique are also presented for comparison and show little difference with the theoretical results.Fig.20 presents the bending curvatures aboutY-axis along the wing span at the same state. The curvatures calculated by the strain-based method are generally in good agreement with the experimental results except the third point. The deviation is mainly due to the measurement error of the third fiber optic sensor, which further leads to the error of the displacements as shown in Fig. 19. In general, the proposed method is proved to be suitable for dealing with nonlinear static aeroelastic problems. Time-domain analysis is then implemented by taking the deformed shape obtained in the static aeroelastic analysis as the initial condition. The responses (from 0 s to 30 s) of the vertical displacement, chordwise displacement as well as twist angle of the wingtip are plotted in Fig. 21. The responses are calculated by giving an initial small velocity disturbance of the element bending strains.The plots of time history at speed 17.5 m/s and 17.6 m/s under 3° AOA show that the nonlinear flutter boundary is about 17.6 m/s, which is much lower than the linear flutter speed. As can be observed from the time history, the amplitude of oscillation initially increases slowly before the 17th second. It then shows exponential increase around the 20th second, but eventually falls into a limited amplitude oscillation.A typical phenomenon is that the chordwise oscillation becomes unstable and participates in the nonlinear flutter. To further analyze the characteristics of nonlinear flutter, the responses in the time domain are transformed into the frequency domain through the Fast Fourier Transform (FFT), as shown in Fig. 22. One can basically find a certain flutter frequency of 7.5 Hz. It can be concluded that chordwise bending mode is coupled with the torsion mode and further causes a substantial decrease in the flutter speed. Fig. 22 FFT of time domain responses. Fig. 21 Time history of wingtip displacement for α=3°. Figs. 23 and 24 show the experimental results of the acceleration response and corresponding FFT results, respectively.The nonlinear flutter speed is approximately 18.5 m/s. As can be observed from the FFT of accelerations, the flutter frequency is 7.6 Hz. Both the flutter speed and frequency show good agreement with the theoretical results,which proves that the presented method provides an acceptable way for predicting nonlinear flutter boundary. Besides, the experimental data indicate that the structural dynamic characteristics can be affected by the large deformation under aerodynamic loads and reflected in the decline of the chordwise mode frequency and eventually the decline of the flutter speed.Both the numerical and test results show that geometrically nonlinear aerolastic analysis is necessary for very flexible wings. Fig. 23 Wind tunnel test results of accelerations under α=3°. Fig. 24 FFT of accelerations for V=18.5 m/s. The nonlinear response of the wing in a gusty environment simulated by the strain-based formulation is plotted and compared to the test results.In these tests,the wing was installed in the same state as in flutter test and the gust generator oscillates to generate continuous sinusoidal gust. Wingtip vertical displacements in the test were obtained from the SDT scheme based on the fiber optic strain data. With a fixed wind speed of 14 m/s,the time history of bending curvatures aboutY-axis at different positions(s=0.1,0.3,0.5,0.7,0.9) under varying gust frequencies from 1 to 3 Hz are plotted in Fig.25.The absolute values of bending curvatures tend to be smaller when approaching to the wingtip. However, the oscillating amplitudes do not necessarily obey the same rule. With the increase of gust frequency, the oscillating amplitudes of bending curvatures near the root decrease obviously, which results in the decrease of the response amplitude of tip vertical displacement. Despite the phase differences, the bending curvatures obtained by the theoretical analysis are generally in good agreements with the test results. The relative deviations tend to be larger when approaching to the wingtip. This is mainly because the absolute values of bending curvatures near the tip are small,which are more sensitive to environmental noise.However,the structural deformations are more sensitive to the root strains rather than the strains near the tip. Thus, the influence of the deviations mentioned above on the calculated structural deformations is acceptable. Fig. 26 plots the time history and FFT of tip vertical displacement under varying gust frequencies from 1 to 3 Hz.For better observation of the oscillating amplitudes, the zero-frequency components are not plotted here. The oscillating amplitudes vary with different gust frequencies. When the gust frequency equals 1 Hz, which is close to the frequency of the first vertical bending mode,the response amplitude is much larger than that at the other two frequencies. From the FFT results, one may find that the main resonant frequencies of the wind tunnel test are not the same as the gust frequencies.This is mainly due to the limitation of the accuracy of the gust generator. Oscillating amplitudes read from the plots of FFT results are presented in Table 3.Despite the phase differences,the stable oscillating amplitudes in the test are quite close to those in the theoretical analysis and the test results, proving that the presented method has reasonable accuracy. Fig. 25 Time history of bending curvatures about Y axis at different positions along wing span: (a) 1Hz, (b) 2Hz, (c) 3Hz. Fig. 26 Time history and FFT of tip vertical displacement for V=14 m/s under different gust frequencies: (a) 1Hz, (b) 2Hz, (c) 3Hz. Table 3 Oscillating amplitude under different gust frequencies. (1) A theoretical framework for nonlinear aeroelastic analysis of flexible wings in the time domain was developed and validated by the correlative wind tunnel tests in present work. The nonlinear structural dynamic equations of motions are established based on the geometrically exact beam model with constant-strain elements.Different from the displacement-based method, strains are chosen to be the primary variables and analytically integrated to obtain structural displacements and rotations.A direct advantage of this formulation in dealing with static problems is the constant stiffness matrix. The unsteady aerodynamic loads calculated by the UVLM were combined with the strain-based formulation for nonlinear aeroelastic analysis. Nonlinear time-domain analyses were performed and compared to the wind tunnel test. (2) A flexible wing model equipped with a novel fiber optic sensing system for measuring structural deformation was tested in a wind tunnel to present typical geometrically nonlinear phenomena and validate the proposed theoretical formulation. Both the experimental and theoretical results of nonlinear flutter analysis demonstrate that the geometric nonlinearity can cause significant changes in the structural dynamic characteristics and must be considered in a nonlinear flutter analysis. The result also demonstrates that the chordwise bending mode might participate in the nonlinear flutter. (3) To study the nonlinear gust response,a gust generator is installed in the wind tunnel to produce continuous sinusoidal gust. Gust responses with a fixed wind speed under different gust frequencies were simulated by the theoretical analysis and compared to the test results.The stable oscillating amplitudes obtained from the theoretical analysis are quite close to the test results, proving that the presented method has reasonable accuracy. The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. This study was co-supported by the National Key Research and Development Program (No. 2016YFB0200703) and Beijing Advanced Discipline Center for Unmanned Aircraft System.









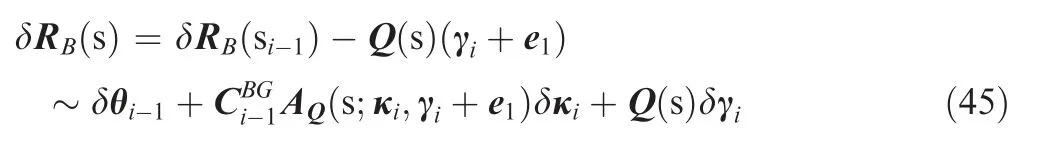





2.2. Unsteady aerodynamics







2.3. Coupling of strain-based beam with UVLM


2.4. Time-domain analysis methodology
3. Experimental design

3.1. Wing model
3.2. Measuring techniques





3.3. Suspension system

3.4. Gust generator



4. Results and analysis
4.1. Validation of strain-based beam formulation





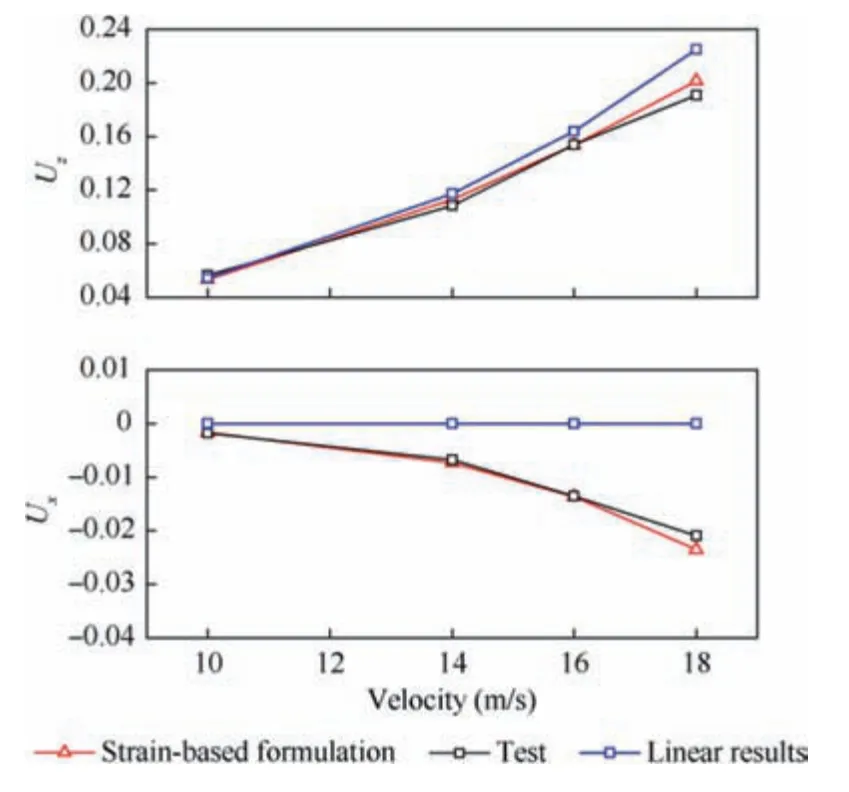
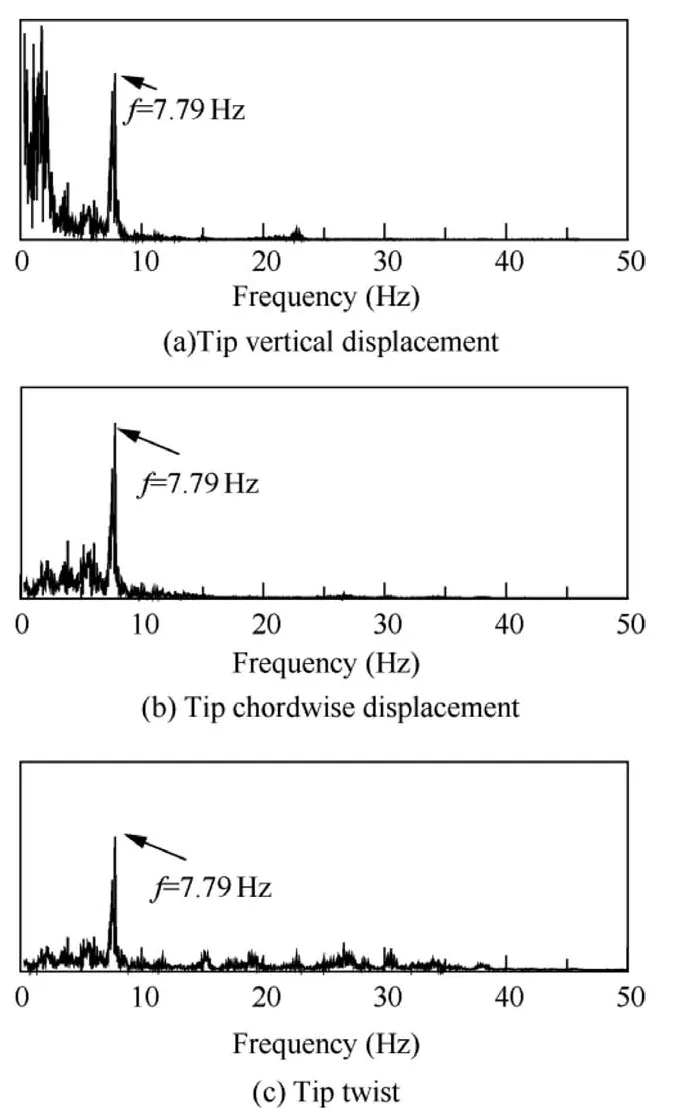
4.2. Flutter analysis and test results






4.3. Gust responses and test results



5. Conclusions
Declaration of Competing Interest
Acknowledgements
 CHINESE JOURNAL OF AERONAUTICS2021年1期
CHINESE JOURNAL OF AERONAUTICS2021年1期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Tangling and instability effect analysis of initial in-plane/out-of-plane angles on electrodynamic tether deployment under gravity gradient
- Aerodynamic periodicity of transient aerodynamic forces of flexible plunging airfoils
- Effects of swirl brake axial arrangement on the leakage performance and rotor stability of labyrinth seals
- Experimental and computational investigation of hybrid formation flight for aerodynamic gain at transonic speed
- Tomography-like flow visualization of a hypersonic inward-turning inlet
- Hypersonic reentry trajectory planning by using hybrid fractional-order particle swarm optimization and gravitational search algorithm
