Stationary non-Gaussian random vibration control:A review

Ronghui ZHENG, Guoping CHEN, Huaihai CHEN

State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

KEYWORDS non-Gaussian random;Kurtosis;Skewness;Power spectral density;Vibration control

Abstract This paper presents a review of the various methods for the stationary non-Gaussian random vibration control.Random vibration tests can be divided,according to the number of exciters,in single-shaker tests and multiple-shaker tests.In the stationary non-Gaussian random vibration test, the time and frequency domain characteristics of the responses should be controlled independently and simultaneously. Skewness and kurtosis are usually selected as the non-Gaussian time control references(targets)while power spectral density is the frequency domain control procedure before it recalls the concepts of non-Gaussianity. Then, the generation of a one frame stationary non-Gaussian random signal for both the single and multiple shakers are reviewed.The commonly used methods for the single non-Gaussian random signal generation in the random vibration test are memoryless nonlinear transformation, phase modification and Filtered Poisson process.For the multiple-shaker case,the sequential phase modification and memoryless nonlinear transformation are used to generate one frame coupled multi-channel non-Gaussian random signal.In order to obtain a stationary and consecutive dynamic input,the time domain randomization procedure is introduced with high computational efficiency and its influences on the skewness and kurtosis are analyzed.Finally,two existing problems in the non-Gaussian random vibration control are addressed.

1. Introduction

In recent years,there is an increasing interest in non-Gaussian random vibration control for replicating a measured dynamic environment or arranging a fatigue test.1-7In a traditional stationary Gaussian random vibration test,only response spectral density in the frequency domain needs to be controlled. The time-domain features of responses are approximately stationary Gaussian due to the linear experimental setting and stationary Gaussian input.8-11

In general, skewness and kurtosis are commonly used to characterize the non-Gaussian distribution.Skewness is a measure of the asymmetry of the probability distribution while kurtosis is a measure of the tailedness of the distribution.Skewness and kurtosis are associated with the third and the fourth moment of the probability density distribution respectively. Theoretically, the probability density distribution function is the best reference definition to depict the non-Gaussian characteristics for a stationary and ergodic stochastic process.12However, in engineering practice, it is not easy to impose a probability distribution reference in the control apparatus due to its multifarious shape. Furthermore, the higher order moments do not carry explicit physical meanings and need substantial measurement information to be estimated accurately.13,14

In a non-Gaussian random vibration test scenario, a non-Gaussian random signal should be generated first.Many methods are available for the creation of a non-Gaussian random signal in the Refs. [15-20] and among them, three methods are mostly employed in random vibration tests which are memoryless nonlinear transformation, phase modification and Filtered Poisson process.Memoryless nonlinear transformation is a classic method to convert a Gaussian random signal to a non-Gaussian random signal in the time domain. The term memoryless means that the transformed data are only determined by the current corresponding data.The key idea of this method is to find a monotonic nonlinear transformation function to modify the amplitudes of the signal in the time domain.Therefore,the obvious drawback of the memoryless nonlinear transformation is that the Fourier amplitudes of the transformed signal are altered compared with the original signal,which introduces some distortions to the power spectral density and leads to a significant loss in the dynamic range.21,22This disadvantage can be overcome by an improved memoryless nonlinear transformation method where an iterative process is used to keep Fourier amplitudes unchanged.22,23Phase modification consists of manipulating the Fourier phase angles of the signal to achieve the desired non-Gaussian random signal. An interesting kurtosis formula expressing via the Fourier amplitudes and Fourier phase angles was derived by Steinwolf et al.24-26.It reveals that the Fourier phase angles have a great impact on the time-domain characteristics of the signal and it shows how a Gaussian and a non-Gaussian random signal can possess the same power spectral density. The last popular method is called Filtered Poisson process where a filter is firstly designed by a certain power spectral density and then a constructed shot noise passes through the filter to obtain the desired non-Gaussian random signal.27,28In addition, an amplitude modulation function can be used to generate a burst non-Gaussian random signal but it is actually a non-stationary random signal.1,29

It has shown that a stationary non-Gaussian random input may not imply a non-Gaussian output for a linear time invariant system in some cases.30-33However, in a non-Gaussian random vibration test, we expect the non-Gaussian behavior at the response control point and usually do not directly generate a stationary non-Gaussian random signal as a dynamic input. In fact, the input signal should be calculated by the input-output relationship and specified reference values. In theory, the statistical features of the measured response coincide with the references where the goal of the random vibration control is achieved. In multi-shaker stationary non-Gaussian cases, the control of multi-output non-Gaussian responses becomes more complicated than the single input single output case due to the coupling problems caused by inherent multiinput multi-output physical system and time-frequency features interactions.23,34The Fourier amplitudes are used to control the power spectral densities while the skewnesses and kurtoses are determined by the Fourier phase angles. Therefore,the Fourier amplitudes and phase angles of the responses should be controlled independently and simultaneously to satisfy the specified references.It was found that the multi-output reference skewnesses and kurtoses cannot be defined arbitrarily because the cross spectral densities have a non-negligible restriction on the settings.34

MIL-STD-810H points out that the ability of modern control systems to account for non-Gaussian features affect the development of laboratory vibration tests.14Although some commercial products for the single input single output non-Gaussian random vibration test by kurtosis control have emerged,the non-Gaussian random vibration control still does not have a uniform standard. This paper reviews the various stationary non-Gaussian random signal generation methods for both the single and multiple shakers random vibration control.It attempts to provide a stationary non-Gaussian random vibration test scenario that can be employed in engineering practice. The remainder of the paper is organized as follows.First of all, for a better understanding of non-Gaussian random vibration control, a general procedure for the stationary non-Gaussian random vibration tests is succinctly introduced in Section 2. Section 3 gives some basic but necessary definitions of the non-Gaussian random signal. The generations of the single and multiple channel one frame non-Gaussian random signals are presented in Section 4 and Section 5 respectively. Procedures for the generation of a multi-shaker continuous dynamic input are provided in Section 6. Discussion is given in Section 7. Finally, conclusion is presented in Section 8.

2. Stationary non-Gaussian vibration control procedure

A general procedure for the single input single output stationary non-Gaussian random vibration test is depicted in Fig. 1.The stationary non-Gaussian random vibration test usually consists of four key parts which are the determination of reference values, identification of unit under test, generation of drive input and control of response output. The detailed steps are described in the following sections and this section gives an overview of the stationary non-Gaussian random vibration test.

Fig. 1 General procedure for stationary non-Gaussian random vibration control.

The reference values are composed of the reference spectrum and reference skewness and kurtosis which are induced from the measured field data or can be set empirically by user.At present,there is no available standard induction method for the measured non-Gaussian random vibration data. In most cases,the user sets a reference kurtosis value and the reference skewness defaults to zero.This is because the encountered non-Gaussian dynamic environments are usually zero mean and symmetric. For the single input single output case, the reference skewness and kurtosis settings have no coupling problem with the reference spectrum definition. But for the multi-input multi-output case,the reference spectral densities have a significant impact on the definition of the reference skewnesses and kurtoses due to the coupled time domain and frequency domain characteristics of the signal.

The system identification is commonly conducted in the frequency domain where the Frequency Response Function(FRF) of the unit under test is estimated by using a low level excitation. A time domain transfer matrix can alternatively be used to characterize the input-output relationship.35,36However, its inverse estimation is computationally intensive because the time domain transfer matrix has a large dimension,especially increasing the number of spectral lines and control points. Therefore, it seems impractical to realize a random vibration control in the time domain unless there is a special requirement to perform it in the time domain.12,37The frequency response function estimation has a direct effect on the spectral control result, particularly in resonance frequencies.33,38

The time domain drive signal is generated by the reference values and frequency response function combined with the inverse Fourier transform. The reference values are first used to generate a reference signal which satisfies the predefined reference spectrum and reference skewness and kurtosis;then the frequency response function is utilized to obtain the desired drive signal. Consequently, the statistical features of the measured response signal will be in accordance with those of the reference signal. In a stationary random vibration test, the dynamic input should be continuous and stationary for a linear time-invariant system. If the junction between two frames is discontinuous, an impact may emerge which may result in the failure of the test and in a worst case also in damage to the experimental equipment. Therefore, the time domain randomization is usually applied to obtain a continuous and stationary dynamic input,39but it also has an influence on the non-Gaussianity of signal.

The drive input determines the response output and conversely the response output is used to update the drive input. The deviations between the responses and references are calculated to correct the drive input with control algorithms in a closed loop equalization way. The control algorithms should be stable and convergent to ensure the reliability of the equalization process.40,41The control accuracy and closed loop speed are the two main performances of the equalization process. The control accuracy indicates the match between the control results and the references;the closed loop speed refers to the time between two consecutive adjustments of the drive input. On the other hand, the response skewness and kurtosis control and response spectrum control should be independent and simultaneous. The Fourier amplitudes derived from the reference spectrum are utilized to control the response spectrum and the Fourier phase angles are supplemented to control the response skewness and kurtosis.

3. Preliminary non-Gaussian definitions

Some preliminary definitions of the non-Gaussian random vibration are introduced in this section. Let us start with the cumulant concept. For a zero mean stationary random signalz(t), thekth cumulant can be expressed as42

where i is the imaginary unit and ω is the circular frequency.Ψ is the second characteristic function and it can be obtained from the first characteristic function Φ as

whereE[·] represents the mathematical expectation andp(z) is the probability density function of the signalz(t).In this paper,the mean value of the random signal is zero. Thekth moment ofz(t) is given by

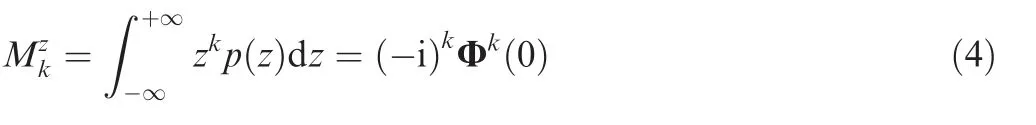
The cumulant and moment have a relationship and they can be expressed and transformed from each other.According to Eq. (1), the first four cumulants can be obtained as42

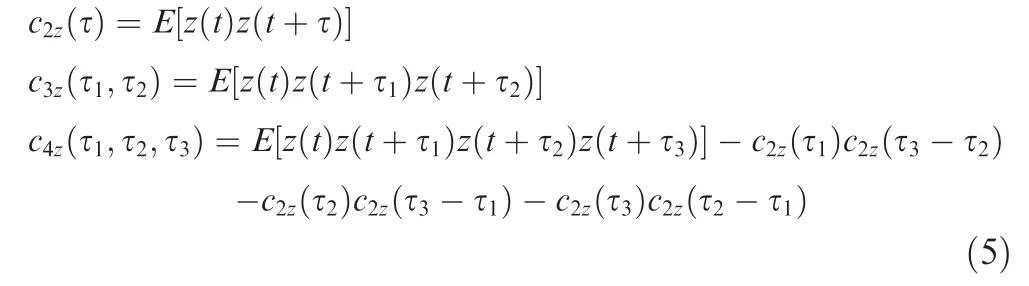
The skewness and normalized kurtosis of the signalz(t)can be expressed as

For a stationary Gaussian or mesokurtic random signal,the skewness and kurtosis equal zero and three respectively.A random signal with kurtosis greater than three is said to be leptokurtic or super-Gaussian and with kurtosis less than three is said to be platykurtic or sub-Gaussian. Fig. 2 shows the different probability distributions of three zero mean random signals with the different kurtoses but a same standard deviation σ. The two non-Gaussian random signals are generated by the memoryless nonlinear transformation which is elaborated in Section 4. It can be seen that the super-Gaussian random signal has the most distribution at the mean and beyond±3σ while the sub-Gaussian random signal has the opposite properties.

Another important definition in random vibration tests is the crest factor (CF) which is expressed as43

where σzis the standard deviation ofz(t).There are some relationships between the crest factor and skewness and kurtosis.When the skewness of the random signal is zero, the absolute values of positive and negative crest factors are approximately equal. The time domain amplitudes of a standard Gaussian random signal are symmetrically distributed and reside in large part(～99.7%)inside a range of three times the standard deviation. For a symmetrical non-Gaussian random signal with a kurtosis value higher than three, a larger part of the amplitudes of the signal exceed three (or more) times the standard deviation.

The coskewness and cokurtosis concepts are used in the multiple channel non-Gaussian random signals analysis.For two stationary random signalsp(t) andq(t), the skewness and kurtosis of summed random signalp(t)+q(t) are given as

Fig. 2 Three probability distributions with different kurtoses(S=0).

whereSppq,Spqq,Kppqq,KpppqandKpqqqare coskewness and cokurtosis terms.Sp,SqandKp,Kqare the skewness and kurtoses ofp(t) andq(t) respectively. σpand σqare the standard deviations ofpandqrespectively. σpqis the covariance. Ifp(t) andq(t) are independent, the Eqs. (9) and(10) are reduced to

It is clear that coskewness and cokurtosis are related to the correlation between the two random signals.

In addition, according to Eqs. (6) and (7) and using the Duhamel integral, the skewness and kurtosis of the response output in a linear time invariant system can be obtained as44,45

wherez(t)is regarded as a drive input.It can be observed that the output skewness and kurtosis depend not only on the inherent system characteristics but also on the features of the input signal.Furthermore,it also explains that why the second order spectrum (power spectral density) is not enough for description of the skewness and kurtosis. From Eqs. (13) and(14), it can be seen that the output skewness and kurtosis are related to the third order spectrum (bispectrum) and fourth order spectrum (trispectrum) of the drive input, respectively.

4. Single channel one frame generation

This section reviews four methods for the generation of one frame single channel stationary non-Gaussian random signal with the desired power spectral density,skewness and kurtosis.Commonly used methods in random vibration tests are the memoryless nonlinear transformation, phase modification and Filtered Poisson process.

4.1. Memoryless nonlinear transformation

The memoryless nonlinear transformation is a classical method to generate a non-Gaussian random signal. The main idea is to find a monotonic nonlinear transformation functiong(·). It can be expressed as

wherex(t)is a Gaussian random signal with a specified power spectral density. The term memoryless refers to the fact that the value ofy(t) at an arbitrary instanttdepends only on the value ofx(t) att. The relationship of the probability density functions of two random signals follows

4.1.1. Hermite polynomial function

The Hermite polynomial function for the memoryless nonlinear transformation proposed by Winterstein can be expressed as46,47

and the Gaussian random signalx(t)has a zero mean and unit variance. The parameterh0is given as

For the parametersh3andh4, three different approximate solutions called first order,second order and third order models can be obtained. The first order model is given as

The transformed non-Gaussian random signaly(t) also possesses zero mean and unit variance and only skewness and kurtosis values are used for the transformation process.From Fig. 3, it can be seen that the three models have some differences in the transformation accuracy where the second and third models are more accurate than the first model.Nevertheless, the practical kurtosis transformation range is not wide and up to about 15.

4.1.2. Cubic polynomial function

The second common nonlinear transformation function is the cubic polynomial function of the form

Fig. 3 Kurtosis transformation accuracy of three different models (S=0).

The monotonicity condition makes the parameters satisfy the following constraints

In this form, the first four moments are used to determine these four parameters using Eq. (17) with a nonlinear optimization method.

4.1.3. Hyperbolic function

A nonlinear transformation function has the form of hyperbolic sine and its inverse as22,23

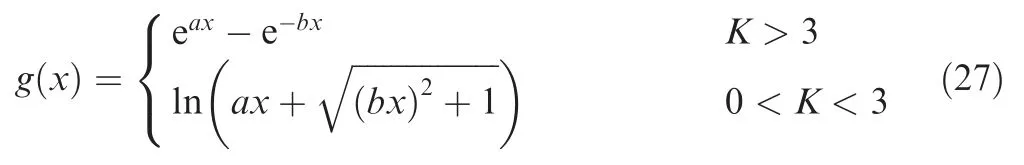
In a case when the parametersaandbare equal,the skewness ofy(t) is zero. A nonlinear optimization or an iterative approach can be used to determine the two parameters. Note that the mean of the signal is assumed zero in this work. In order to remain the variance unchanged before and after transformation, the standard deviation ofy(t) can be rectified by

where σyis the standard deviation of（t）after the transformation but before the rectification.σxis the standard deviation ofx(t).It is found that the Taylor expansion of Eq.(27)is a Polynomial form, i.e.

It has only two parameters to control the skewness and kurtosis. If Eq. (28) is not adopted, two additional parameters should be supplemented to control the mean and standard deviation (d=0 if the mean is zero), such as

When the parametersaandbare equal, an approximate closed solution for kurtosis control in Eq. (27) is given as

Note that the amplitudes of×in Eq. (27) should be normalized asx～=x/|x|maxbefore the parametersaandbare determined by Eq. (31). The mean and variance ofy(t) can be modified using Eq. (28). The transformation accuracy is given in Fig. 4 and it shows a good kurtosis transformation result.

4.1.4. Sarkani transformation function

A nonlinear transformation function proposed by Sarkani has the following form48

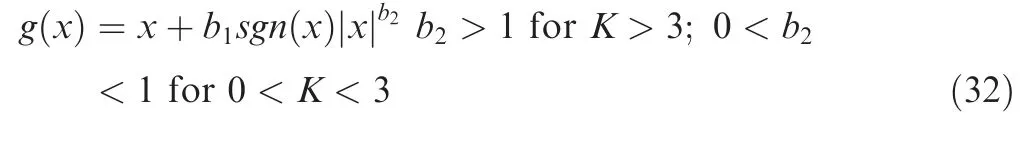
Fig. 4 Kurtosis transformation accuracy of Eq. (31) (S=0).

Fig.5 Output kurtosis with two parameters in Eq.(32)(S=0).

The two parameters are confined to positive values to satisfy the monotonicity condition. Fig. 5 shows the output kurtosis changes with the two parameters and it is found that whenbequals 1, the transformed signal is approximately Gaussian.Only a non-Gaussian random signal with zero skewness can be generated with this nonlinear transformation function. The two parameters are used to control the kurtosis ofy(t). The mean and variance ofy(t) can be modified using Eq.(28).

4.1.5. Smallwood transformation function

An inverse function of Eq.(15)given by Smallwood is used for the non-Gaussian random signal generation.17It is expressed as

Fig. 6 Improved memoryless nonlinear transformation method.

The optimization method is used to find the most adequate parametersc1,c2,c3,c4, α and β for the given skewness and kurtosis values. The parameterc2is found to be necessary to force the mean to zero in some cases and it is the only parameter allowed to be negative.

4.1.6. Improved nonlinear transformation method

The memoryless nonlinear transformation method is computationally efficient. However, the memoryless nonlinearity has a whitening effect49and the power spectral density is altered to a certain degree after the transformation which is reflected in a loss of the dynamic range.21,22This is because both the Fourier amplitudes and Fourier phase angles are modified to obtain the desired non-Gaussian features during the transformation process.To overcome this disadvantage,the improved nonlinear transformation method(see Fig.6)can be used to guarantee the Fourier amplitudes preservation22,23.Therefore,it is,in essence, a kind of phase modification method.

The fundamental principle of the memoryless nonlinear transformation method is to modify the amplitudes of the random signal in the time domain.It is an intuitive way to control the skewness and kurtosis. As shown in Fig. 7, for kurtosis greater than three,the smaller amplitudes of the random signal are further reduced whereas few large amplitudes are increased.Therefore,the kurtosis of the random signal is tuned to increase.Conversely,for kurtosis less than three in this case,all the amplitudes of the random signal are increased and have a tendency to be equal.

Fig. 7 Three memoryless nonlinear transformation functions.

4.2. Phase modification

4.2.1. Steinwolf analytical formula

There are many phase modification methods,among which the Steinwolf analytical formula is the most used one.24-26The analytical expressions of skewness and kurtosis explain the basic principle of the phase modification method. Because the power spectral density is only related to the Fourier amplitudes, the Fourier phase angle tuning process does not affect the power spectral density but it affects the time domain characteristics.

According to the definition in Eqs.(6)and(7)and by using some integral operations, the skewness and kurtosis can be expressed by the Fourier amplitudesAand phase angles φ as

whereNis the length of the signal.If the Fourier phase angles are uniformly distributed on the range[-π,π],the synthesized random signal is approximately Gaussian.If the arguments of cosine functions are set to zero by virtue of one of the phase angles being expressed via the others, then the members of the summation are forced into their maximum possible values and therefore it results in a tendency for the skewness and kurtosis to increase. It is noted that the skewness and kurtosis modification processes affect each other and an iterative tuning process is required to achieve the desired result. In addition,the Fourier phase angles are complex conjugate symmetric.The phase modification method is computationally intensive if the reference kurtosis is large or skewness and kurtosis are considered simultaneously.

4.2.2. Direct formula method

The discrete form of the random signalz(t) can be written as

Each amplitude of the random signal in the time domain is related with all the Fourier amplitudes and phase angles in the frequency domain. As mentioned above, for a non-Gaussian random signal with kurtosis greater than three, some of the amplitudes exceed three or more times the root mean square level.Some amplitudes ofzkcan be tuned to increase its absolute values to increase the kurtosis.

Eq. (37) shows that eachzkis composed ofNcosine functions whose values are influenced by the Fourier phase angles φn. If the subscriptkofzkis specified aspand the Fourier phase angles are modified to make the values of the cosine functions approach to 1 or -1, the absolute value ofzpincreases and a peak in time history atppoint is produced.Thus, the kurtosis of the signal increases. This is an intuitive kurtosis tuning method and it can be used only for the generation of a non-Gaussian random signal with kurtosis greater than three.

Therefore, the direct formula method for kurtosis tuning can be expressed as

The positionpcan be randomly selected from 1 toNor an absolute large amplitude can be chosen, and then the sign of thezpis checked. According to Eq. (37), ifzpis greater than zero, the value of the cosine function is set to 1 by means of a modification of the Fourier phase angles, sozpincreases in a positive direction which results in a tendency for a kurtosis increase. Similarly, ifzpis negative, the value of the cosine functions is set to -1 to produce a peak in negative direction for, again, a kurtosis increase. The skewness can also be controlled by modifying some of amplitudes of the random signal.

4.2.3. Other methods

A non-uniform phase distribution method proposed by Hsueh and Hamernik is to use on-band and off-band Fourier phase angles with a Gaussian or uniform distribution for kurtosis tuning.50More generally,the Fourier phase angles in on-band segment can be set to zeros that an extreme peak is produced in the middle of the random signal.Smallwood proposed a two β distributions phase modification method to generate non-Gaussian random signal with kurtosis greater than 3.19The first β distribution with two parameters are used to pick the random phase angles for kurtosis control while the second one is to determine the random circular shifts for periodicity control.The random signals with kurtosis larger than 3 can be generated with this non-uniform phase distribution method. Seong and Peterka constructed the Fourier phase by adding the four phase angles that are parametrized with four scalar parameters.51The non-Gaussian features are obtained by a direct control of the individual spikes such as the frequency of occurrence.

4.3. Filtered Poisson process

4.3.1. Smallwood method

A Filtered Poisson process,also called a generalized shot noise process, is characterized by pulses of random shape or of deterministic shape and random magnitude arriving at random times.A method with the Filtered Poisson process proposed by Smallwood is introduced.52The shot noise processs(t) can be expressed as

where τkare independent random times governed by an exponential distribution with an average rate of λ occurrences per second.h(t) is calculated from a given power spectral density with the inverse Fourier transform as

An independent amplitude parameterBis supplemented to the Eq. (39) and the output random signalz(t) can be expressed as

IfBand τ are independent,and the mean of τ is long compared to the duration ofh(t), then one can have

Three amplitude parameter forms combined with their first four moments are presented. For example, ifBfollows a normal distribution described with a mean μBand standard deviation σB, we have

Therefore, combining the Eqs. (6), (7) and (44), the unknown parameters can be determined according to the specified skewness and kurtosis.

4.3.2. Van Baren method

Van Baren generated the non-Gaussian random signal by using the shot noise process but with a different definition of target non-Gaussian random signal as52

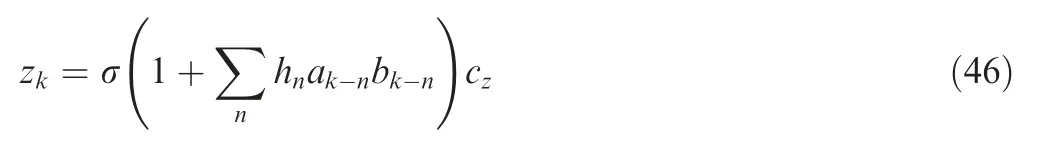
wherehis the filter impulse response function obtained from a given power spectral density.ais the arbitrary independent identically distributed random sequence.bis the shot noise sequence.cis the unit variance, zero mean and independent identically distributed Gaussian random sequence.σ is the normalization factor that is used to guarantee the unit variance of the signal. The solution for the kurtosis control is available in the patent.

4.4. Time series

Consider a general autoregressive moving average series model

wherexandyare the input and output random time series respectively.aandbin Eq. (47)are the model constant coefficients,pandqare the model orders.Research shows that there is a linear relationship of skewness and kurtosis between the stationary input and output random signals.53,54In fact, if a linear time invariant system is used to filter the input random signal, the output can be written as a form of linear convolution

wherehis the impulse response function of the system and it can be obtained from the specified power spectral density function.

In such a model, if the input is an independent identically distributed stationary random process, the linear relationship of skewness and kurtosis between the input and output usually follows

where the parametersAt,BtandCtare associated with the designed linear system. Therefore, it requires a non-Gaussian input to obtain a desired non-Gaussian output. The Johnson transformation system can be used to generate a zero mean non-Gaussian white noise sequence as the input random signal. The unbounded Johnson system is given as55

It is an inverse hyperbolic sine form and four parameters are used to determine the first four moments. Similarly, the parametersaJandbJcan be ignored and Eq. (28) is used to correct the standard deviation. For a first order model of autoregressive moving average series, the three parameters given by Davies et al.56(b0=1) are

If more orders are involved, it is complex to determine model parameters for generating a desired non-Gaussian random signal for vibration testing purpose.Furthermore,a non-Gaussian random signal should be generated first, which makes the synthesis procedure complicated.

4.5. Brief summary

We evaluate these generation methods for the single channel one frame non-Gaussian random signal. As listed in Table 1,it can be concluded that among these methods the improved memoryless nonlinear transformation is a best choice to generate a desired one frame non-Gaussian random signal. As analyzed above, the improved memoryless nonlinear transformation is a kind of phase modification method. For the multi-channel coupled non-Gaussian generation,the phase modification exhibits an obvious advantage over other methods which is explained in the next section.

Table 1 Comparison of five non-Gaussian generation methods.

5. Multiple channel one frame generation

For a multi-input multi-output random vibration test,not only the auto power spectral densities are defined,but also the cross power spectral densities need to be considered.57The auto power spectral densities represent the vibration levels at the control points while the correlations among such points are characterized by the cross power spectral densities. The difficulty of multi-shaker non-Gaussian random vibration control lies in the complex coupling problems due to the inherent multi-input multi-output physical system and the presence of the cross power spectra. The inherent physical coupling refers to the fact that the response at a control point is affected by all the inputs. This section utilizes the sequential phase modification23and memoryless nonlinear transformation16to generate multi-channel one frame non-Gaussian random signal.

5.1. Sequential phase modification

For anninputnoutput linear time-invariant dynamic system(nis a positive integer,n≥2), the positive definite reference spectral matrix at each spectral line can be expressed as

where the diagonal elements are auto power spectra and the off-diagonal elements are cross power spectra.γ2and α are the coherence and the phase difference with the ranges of[0,1)and[-π,π]respectively.The Cholesky decomposition is performed to the reference spectral matrix as

where Lris a lower triangular matrix and the superscript ‘H’denotes the complex conjugate transpose.

Due to the lack of Fourier phase information for the inverse Fourier transform,a random phase matrix Θ with uniform distribution is introduced as34

wherelr,jk(j,k=1,2,...,n;j≥k) are the elements of Lr. Each column is coupled with an independent noise source and each row must be summed to guarantee the cross power spectral information.34,39In the sequential phase modification,the random phase angles must be manipulated from θ1to θnsequentially to avoid cross couplings. The improved memoryless nonlinear transformation can be used to modify the random phase angels. If θ1is modified to make the skewness and kurtosis of channel one satisfy reference values, the random signals of the first column in U are all determined due to the modified θ1. Subsequently θ2is modified to make channel two satisfy the reference requirements. The random signal of the channel two is a summed signal and only θ2can be used to modify to control the skewness and kurtosis. Eqs. (11)and (12) can be used to determine the modification of θ2.Therefore, the diagonal random phase angles can be modified sequentially for each channel to obtain the non-Gaussian control.

It is clear that the reference spectra are used to provide the Fourier amplitudes and the reference skewnesses and kurtoses are used to determine the Fourier phase angels.From Eq.(54),the time domain random signal u can be obtained by the inverse Fourier transform as34

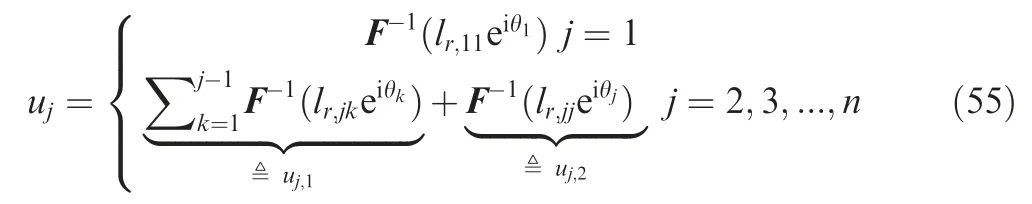
where F-1denotes the inverse Fourier transform operation.The key idea of the sequential phase modification method is to sequentially manipulate the random phase angles θ, that is to manipulate the skewnesses and kurtoses of the diagonal random signalsuj,2.The skewness and kurtosis ofuj,2that need to be adjusted can be expressed as34

Sj,1andSj,2are the skewnesses ofuj,1anduj,2andKj,1andKj,2are the kurtoses ofuj,1anduj,2, respectively. σj,1and σj,2are the standard deviations ofuj,1anduj,2respectively.SjandKjare thejth reference skewness and kurtosis respectively.

5.2. Memoryless nonlinear transformation

The sequential phase modification method consists in modifying the Fourier phase angles and therefore the power spectral densities remain unaltered. This subsection presents a memoryless nonlinear transformation method where all the channels are transformed to the desired non-Gaussian random signals simultaneously.

After supplementing the uniform distributed random phase angles to the matrix U, the inverse Fourier transform is performed and then the rows of the resulting matrix are summed to form a vector of coupled random signals. It can be expressed as55

where Δfis the frequency resolution.Because of the uniformly distributed random phase angles,the generated random signals in Eq.(59)are approximately Gaussian.The memoryless nonlinear transformation method is then used to all channels to obtain the desired non-Gaussian random signals as5

The improved nonlinear transformation method cannot be used here otherwise the cross spectral densities would be affected. The reason is that every channel random signal(j≥2) expressed in Eq. (59) is coupled with more than two independent random signal sources. The advantage of this method is the high computational efficiency. The obvious drawback is that the power spectral densities are changed to some extent.

6. Continuous input random signal generation

The Sections 4 and 5 elaborate the generation of the one frame single and multiple stationary non-Gaussian random signals.Such generated random signal satisfies the predefined reference spectrum and reference skewness and kurtosis simultaneously and therefore it is called the reference signal.The reference signal and the frequency response function are then used to generate a desired drive input. This section discusses the random vibration control based on the time domain randomization technique. Because the single input single output is a special case of the multi-input multi-output random vibration control,we only present the method to generate the multi-input drive signals for multi-exciter stationary non-Gaussian random vibration test.

6.1. Time domain randomization

The time domain randomization method is to use one frame random signal to compose the continuous random signals with a high efficiency.39There are usually four steps in the process as shown in Fig.8.A circular shift of one frame non-Gaussian random signal is performed first to obtain a reconstructed random signal and then a random reverse operation is used.These two steps are repeated several times to generate many frame random signals which are later windowed and overlapped to compose stationary and continuous random signals.

The influences of these steps in stationary non-Gaussian random vibration control are analyzed here. The circular shift step does not change the skewness and kurtosis of the signal because the amplitudes of the time domain data are not changed but a linear phase shift is introduced into all the frequency components. The random reverse step has an influence on the skewness control. If the reference skewness is set to zero, this step should be used to ensure the symmetric features of the signal. If not, this step should be ignored. The windowing and overlapping steps have a linear effect on skewness and kurtosis of the signal. The skewness and kurtosis of the signal before and after the time domain randomization process can be expressed as58

wherewis the window function andTis the time of one frame random signal.lis the overlap factor. Smallwood suggested a useful class of windows39and its discrete form is given by

Ifm=1,g0=0.5 andg1=0.5, the Hanning window is obtained and an overlap factor of 3 makes the output signals stationary.

6.2. Multi-input drive generation

For the multi-input drive generation, the one frame non-Gaussian random signal achieved by the two methods described in Section 5 is utilized to generate the continuous random signals in different ways.The time domain randomization procedure is suitable for the first case.34The Fourier drive spectral matrix is given as

For the first drive generation, it has

After modification of the random phase matrix Θ as described in Section 5.1, the matrix X is then transformed to a time domain matrix by the inverse Fourier transform. The circular shift and random reverse steps are performed to all columns of the resulting matrix and different columns should have different circular shifts, then each row of the matrix is summed to guarantee the cross spectral densities. Finally, the windowing and overlapping steps are used to compose a continuous drive input.

The time domain randomization cannot be used in the second case where the one frame non-Gaussian random signal is obtained by the memoryless nonlinear transformation method.But a similar procedure can be used to generate the continuous random signals. The one frame non-Gaussian random signal should be generated in succession as described in Section 5.2 instead of the circular shift and random reverse steps; in the meantime, the drive signals are obtained by the generated non-Gaussian random signals and frequency response functions with the windowing and overlapping operation.23

In the closed loop equalization process,the drive input signals are usually updated according to the deviations between the responses and references by the control algorithms as

where Lnew, Snewand Kneware used to update the drive input in Eq.(64).Lyand Loldare the Cholesky decomposition of the present and last response spectra respectively.Syand Syare the present response skewnesses and kurtoses respectively. SRefand KRefare the reference skewnesses and kurtoses respectively. Soldand Koldare the last response skewnesses and kurtoses respectively. ηL, ηSand ηKare spectral, skewness and kurtosis convergence coefficients respectively.

7. Discussion

7.1. Kurtosis performance

Currently, the kurtosis is usually chosen as the non-Gaussian control target and the skewness is set to zero. However, a potential problem is that the performance of the generated non-Gaussian random signal may be different as shown in Fig. 9. The two segment non-Gaussian random signals have the same length and the same kurtosis but they show different time domain features due to the uncontrolled higher moments.If the crest factor is set as an additional parameter to control the kurtosis performance of the signal, it may be better than the method that only kurtosis is controlled.When the skewness is set to zero, the crest factor in Eq. (8) can be written as

However, on the other hand, if the crest factor is considered it will make the non-Gaussian random vibration control schedule more complicated. Therefore, in general,when using a different non-Gaussian random signal generation method, a different control result with a different kurtosis performance may be obtained. This difference may have a significant influence on the subsequent structural behavior evaluation, such as the fatigue life. The problem should be further investigated.

Fig. 9 Two random signals with a same standard deviation(σ=1) and a same kurtosis (K=8).

7.2. Reference kurtoses

In multi-exciter non-Gaussian random vibration control test,the reference spectral densities have a significant impact on the definition of the reference kurtoses.This is because the time domain and frequency domain characteristics of the signal are coupled in the multi-point case.Here,we setn=2 as an example.The power spectral densities of two channel and coherence and phase coefficients are all set to constants at each spectral line. The matrix U can be expressed as

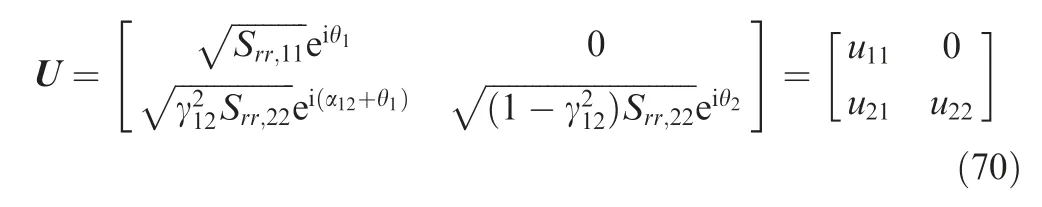
It is obvious that theu21andu22in Eq. (70) are mutually independent due to the different random phase sources.According to Eq. (57), we have

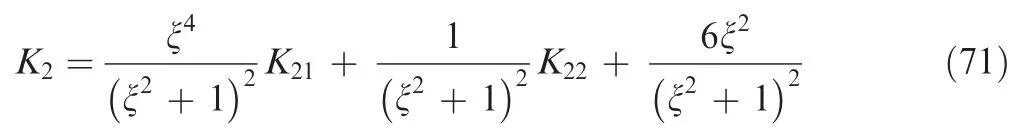
whereK2is the reference kurtosis of a random signal of the channel two that it is the summation ofu21andu22.K21andK22are the kurtoses ofu21andu22respectively. ξ is given by

If the coherence coefficient is one,u22equals zero.It means that when the kurtosis of channel one is determined, the kurtosis of channel two is also determined due to the fixedu21.From Eq.(71),the kurtosis valueK2depends on the parameter ξ and kurtosis valueK22. The contribution ofK22toK2is related to the parameter ξ. A large value ξ makes 1/(ξ2+1)2very small so that the contribution ofK22is limited, as shown in Fig. 10. It is a special two-output case where the reference values are all set to constants.For a general multi-output case,the parameter ξ is expressed by an integral form that is associated with the auto power spectral density,coherence and phase coefficients as34

Fig.10 Relationships between coherence and ξ and 1/(ξ 2+1)2.

The above analysis is in connection with the sequential phase modification. When it comes to the memoryless nonlinear transformation method as described in Section 5.2,the reference kurtosis setting has no restrictions but the price of the spectral changes. In terms of the actual physical situation, it is improper to set the reference kurtoses arbitrarily with the memoryless nonlinear transformation method.In fact,no matter what method is used,the core principle is to adjust the diagonal phase angles or adjust the diagonal random signal sources in Eq.(70).In this way,it can be ensured that the power spectral densities and kurtoses are controlled independently and simultaneously.

8. Conclusion

In applications to non-Gaussian random vibration tests, the skewness and kurtosis are usually regarded as the non-Gaussian control references in the time domain.There are several methods to generate a stationary non-Gaussian random signal, among which the memoryless nonlinear transformation, phase modification and Filtered Poisson process are the most used. Since the power spectral density is related only to the Fourier amplitudes,the skewness and kurtosis can be modified by manipulating the Fourier phase angles. Therefore, the time-frequency characteristics of the output signals can be controlled independently and simultaneously. In the multishaker case, the sequential phase modification is employed to overcome the coupling caused by the cross spectral densities.As alternative, the memoryless nonlinear transformation can be used to generate the multi-channel non-Gaussian random signal but with the disadvantage of spectral distortion.

Although the non-Gaussian random vibration control has made progress, some problems still remain. At present, the skewness and kurtosis are the desired non-Gaussian features,usually kurtosis in particular. However, due to the uncontrolled higher moments,there may be different kurtosis performances using different non-Gaussian generation methods.The reference multi-output kurtoses definition is also challenging due to the presence of the cross spectral densities.Some studies have been done to implement a stationary non-Gaussian random vibration test both in the single and multiple shakers case.In general, it needs more efforts to improve the non-Gaussian random vibration control theory, and to develop more accurate non-stationary random vibration control methods.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This study was co-supported by the Priority Academic Program Development of Jiangsu Higher Education Institutions,china.