Micro-mechanical model for predicting the elasto-plastic behavior of composites based on secant formulation method

Junho LIANG, Xinhi HE, Wenlong TIAN

a School of Materials Science & Engineering, Xi’an Polytechnic University, Xi’an 710048, China

b Shaanxi Key Laboratory of Surface Engineering and Remanufacturing, Xi’an University, Xi’an 710048, China

c School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an 710072, China

KEYWORDS Elasto-plastic behavior;FE homogenization;Mean-field homogenization;MT-DI model;Secant formulation

Abstract To predict the Elasto-Plastic Behaviors(EPBs)of aligned inclusions reinforced composites,this paper develops an interpolative Mori-Tanaka/Double-Inclusion(MT-DI)homogenization model with the secant formulation,and gives the numerical implementation algorithms of the developed MT-DI model with the secant formulation.The Finite Element(FE)homogenization method is implemented to provide the‘‘exact”EPBs of the composites and thus validate the MT-DI model with the secant formulation.The MT-DI model with the 2nd-order secant formulation is validated to provide the more accurate predictions,while the MT-DI model with the 1st-order secant formulation always gives the stiffer predictions. The results show that using the macro-stress and macrostrain as the inputs, the MT-DI model with the secant formulation gives the identical predictions.The predictions of the MT-DI model with the secant formulation vary between those of the MT and DI models with the secant formulation.Meanwhile,the MT-DI model with the secant formulation does not predict the accurate EPBs for the phases of the composites.

1. Introduction

The accurate characterization of the thermo-mechanical behaviors of composites involved in the processing procedure and product service is of significance. This is due to the fact that it benefits the applications of the existing composites,but also provides a basis for the design of new composites.1In tandem with this, one of the most important thermomechanical behaviors of composites is the Elasto-Plastic Behavior(EPB),which could be accurately estimated by using the numerical simulation methods. The prior arts on the modeling and prediction of the EPBs of composites are mainly classified into the following categories:(A)asymptotic homogenization method,2-4(B) Finite Element (FE) homogenization method,5-7(C)mean-field homogenization method8-10and(D)model reduction method.11-13In this work, the mean-field homogenization method is employed to predict the EPBs of composites due to its high computational efficiency and acceptable prediction accuracy.

For the mean-field homogenization method,various meanfield homogenization models have been developed to predict the thermo-mechanical properties of composites. The Mori-Tanaka(MT)model14and the Double-Inclusion(DI)model15are the most widely used mean-field homogenization models and provide perhaps the best predictions of the thermomechanical properties of composites.However,it is found that the ‘‘exact” thermo-mechanical properties (It assumes that they are provided by using the FE homogenization method)of composites vary between those predicted by using the MT model (lower bound) and the DI model (upper bound) for the composites with high inclusion volume fraction.16Therefore, the quadratic interpolative MT-DI model on the basis of the MT and DI models is proposed to predict the more accurate thermo-mechanical properties of the composites with high inclusion volume fraction.16,17

To predict the EPBs of composites, the tangent or secant stiffness tensor to linearize the EPBs of the phases of composites is generally introduced in the mean-field homogenization method. Originating from the seminal work of Hill,18the tangent stiffness tensor method (known as the tangent formulation method as well) linearizes the constitutive law of the relevant phase of composites to the incremental form and introduces the consistent elasto-plastic tangent tensor to compute the EPBs of composites.19,20The tangent formulation method has been widely used for predicting the EPBs of composites by combining with the mean-field homogenization models. Pettermann et al.21introduced the tangent formulation method and developed an incremental MT model to predict the EPBs of aligned inclusions composites, and the method was validated by the FE homogenization method.Doghri and Ouaar22adopted the MT and DI models with the tangent formulation to successfully determine the EPBs of spherical particles composites. However, the mean-field homogenization models with the tangent formulation generally overestimate the flow stress of the relevant phase of composites and thus provide the stiffer EPBs of composites,due to the anisotropic nature of the consistent tangent stiffness tensors.23

The limitation of the tangent formulation method advances the development of the secant formulation method to deal with the EPBs of composites,24,25in which the secant stiffness tensor of the relevant phase of composites is introduced to compute the EPBs of composites. The EPBs of composites predicted by the secant formulation method are much closer to the ‘‘exact” EPBs of composites. However, the overestimation of the flow stress of the relevant phase still exists,since the plastic strain of the relevant phase is determined based on the equivalent stress calculated from the volumetric average of the 1st-order moment of the stress of the relevant phase. This equivalent stress is,however,lower than the average equivalent stress because of the existing large stress gradient in the relevant phase.To overcome this problem,the secant formulation method is modified and the equivalent stress of the relevant phase is computed from the volumetric average of the 2ndorder moment of the stress of the relevant phase.26Gonza´lez et al.27introduced the MT model with the modified 2ndorder secant formulation to investigate the EPBs of composites, and the method was turned out to provide the excellent prediction of the EPBs of composites.

In this work,an interpolative MT-DI model with the secant formulation is developed to predict the EPBs of aligned inclusions composites, and the numerical implementation algorithms of the developed MT-DI model with the secant formulation are detailed. To validate the MT-DI model with the secant formulation, the FE homogenization method is implemented to provide the ‘‘exact” EPBs of the composites.Meanwhile,the capability of the MT-DI model with the secant formulation at both the composite and phase (i.e., matrix and fiber) levels is assessed.

2. Mean-field homogenization method

2.1. General mean-field homogenization theory

Given a Representative Volume Element (RVE) ω of aligned ellipsoidal inclusions composites, the RVE ω consists of the matrix(phase 0,ω0)and the inclusions(phase 1,ω1).The volume fraction of the matrix and inclusions arev0=V0/Vandv1=V1/V=1-v0, whereV0,V1andVare the volumes of the matrix, inclusions and RVE, respectively. The common interfaces between the matrix and inclusions are perfect.

Regarding the micro-field μ(x)of the material point x in the RVE, the following volume average functions are defined firstly:

where 〈·〉 means the average amount; μ0and μ1are the microfields of the matrix and inclusions, respectively. The averages over the RVE, matrix and inclusions are then related by

On the one hand, given that the RVE is imposed a macroscopic linear displacement boundary condition, the average strains of the RVE, matrix and inclusions are related through the strain concentration tensors A0, A1and Aεas28

where ε0, ε1and ε are the strains of the matrix, inclusions and RVE, respectively; A0and A1take the form of Aεand have

where I is the fourth-order unit tensor. The stiffness tensor C of the composites is then computed as

where C0and C1are the stiffness tensors of the matrix and inclusions, respectively.

On the other hand, given that the RVE is subjected to a macroscopic uniform tensile boundary condition, the average stresses of the RVE, matrix and inclusions are analogically related through the stress concentration tensors B0and B1:

where σ0,σ1and σ are the strains of the matrix,inclusions and composites, respectively. The expressions of B0and B1are given as

where M0=(C0)-1and M1=(C1)-1are the compliance tensors of the matrix and inclusions, respectively. For the specified homogenization model, the compliance tensor M of the composites is then derived as

2.2. Interpolative MT-DI model

The fundamental solution of the Eshelby’s single inclusion problem29consisting of an infinite matrix with the stiffness C0and an ellipsoidal inclusion (ω1) with the stiffness C1, is the basis of the various mean-field homogenization models.In the Eshelby’s single inclusion problem, the strain of the inclusion is proved to be uniform and associated with the remote uniform strainimposed on the boundary of the infinite matrix by

where Hεis the strain concentration tensor of the inclusion:

where S is the Eshelby’s tensor, which is computed using the matrix Poisson’s ratio ν0and the inclusion aspect ratio α,and its explicit components for various inclusions are given in Ref.23.

For aligned ellipsoidal inclusions composites, the MT model14is one of the most widely used homogenization models, and the strain concentration tensorof the MT model is identical with that of the Eshelby’s single inclusion problem:

The interpolative DI model15is another most widely used homogenization model and the corresponding strain concentration tensoris formulated as

Based on the DI and MT models,the quadric interpolative MT-DI model is proposed to more accurately predict the elastic properties of the composites:16

3. Secant homogenization approach

For aligned ellipsoidal inclusions composites, the mechanical properties of the inclusions are modeled as elastic:

where the mechanical property of the matrix is modeled as elasto-plastic (σ0（x）=σ0（ε0（x）） with x ∈ω0, and follows the von Mises yield criterion with the isotropic hardening law:

On the other hand, the inclusions are elastic and the average stress and strain tensors 〈σ1〉 and 〈ε1〉 of the inclusions are formulated as

and

wherek1is the secant bulk modulus of the inclusions;μ1is the secant shear modulus of the inclusions.

In the secant formulation method,the average stress tensor〈σ〉of the composites can be computed successively and univocally (historically independent) from the average strain tensor〈ε〉, or vice versa:

where Csand Msdesignate the secant stiffness and compliance tensors of the composites, respectively. Therefore, the secant formulation method is limited to monotonic and proportional loading and thus cannot be applied to the load reversal or cyclic loading cases.

The equivalent stress (Eq. (20)) of the matrix is calculated using the volumetric average of the 1st-order or 2nd-order moment of the stress σ0of the matrix:

According the Hill-Mandel principle,28the average stress and strain of the composites are identical to their macrostress and macro-strain, which reads as

4. Numerical implementation algorithm

4.1. Strain based implementation algorithm

4.2. Stress based implementation algorithm

5. Results and discussion

The FE homogenization method is employed to validate the MT-DI model with the secant formulation in terms of the determination of the EPBs of aligned inclusions composites,due to its excellent prediction accuracy,23,30and the FE homogenization of the EPBs of the composites is implemented in the ABAQUS/Standard.31To predict the EPBs of the composites, the RVEs characterizing the micro-structures of the composites should be generated firstly.Here,the modified random sequential absorption technique32,33is used for generating the RVEs of the composites, and the periodic RVEs of the composites are preferred, as diagrammatically shown in Fig. 1(a). Fig. 1(b) illustrates the generated periodic RVE of the composites, in which the volume fractionv1, aspect ratio α and semi-minor axisbof the inclusions are 20.0%, 2.0 and 2.5 μm,respectively.To avoid the distorted elements,the minimum separation distance (i.e. 0.05b) between the inclusion and matrix and between the inclusions is recommended.32,33The inclusions are meshed by using the 4-node linear tetrahedron elements, while the matrix is meshed by using the modified 10-node quadratic tetrahedron elements to better capture the strain gradient in the matrix and minimize the volumetric locking during deformation of the matrix. Regarding the boundary condition, the periodic boundary condition34,35is adopted and the numerical implementation algorithm of the periodic boundary condition is detailed in our previous work.35

The studied composites are the aligned ellipsoidal SiC inclusions (aspect ratio of 2.0) reinforced aluminum alloy matrix composites (SiC/Al composites).22The mechanical properties of the matrix and inclusions are given as follows:elastic modulusE0=75.0 GPa, Poisson’s ration ν0=0.30,k=400.0 MPa,n=0.25, σ0，y0=75.0 MPa andE1=400.0 GPa, ν1=0.20, and the matrix and inclusions are perfectly bonded.

Fig. 1 A RVE of the composites reinforced by elliptical inclusions with volume fraction of 20.0%, aspect ratio of 2.0 and length of semi-minor axis of 2.5 μm.

Using the MT-DI model with the macro-stress and macro-strain as inputs, the uniaxial tensileand shearEPBs of the composites with the different inclusion volume fractions(v1)are simulated and given in Figs.2 and 3,respectively. The results demonstrate that the identical predictions of the EPBs of the composites are obtained by using the macro-stress and macro-strain as inputs. Therefore, all the simulations hereafter is numerically implemented by using the macro-strain as input, unless otherwise indicated. For the composites withv1of 0.20 and 0.50, the uniaxial tensile and shear EPBs predicted by using the MT,MT-DI and DI models are given in Fig. 4, which shows that the predictions of the MT-DI model vary between those of the MT and DI models,and are close to those of the MT model whenv1is lower.

Regarding the uniaxial tensile and shear EPBs of the composites withv1of 0.20, the predictions of the MT-DI model with the 1st-order and 2nd-order secant formulations are illustrated in Fig. 5, in which the ‘‘exact’’ predictions of the FE homogenization method are plotted as well.It can be seen that the predictions of the MT-DI model with the 2nd-order secant formulation method agree well with the ‘‘exact” result, while the MT-DI model with the 1st-order secant formulation method always predicts the stiffer EPBs of the composites.Meanwhile,the modeled biaxial tensile and tensile/shear EPBs of the composites are presented in Fig. 6, which demonstrates that the MT-DI model with the 2nd-order secant formulation provides the wells predictions of the EPBs of the composites.

Fig.2 Uniaxial tensile and shear EPBs of the composites simulated by MT-DI model(1st-order method)with macro-stress and macrostrain as inputs.

Fig 3 Uniaxial tensile and shear EPBs of the composites simulated by MT-DI model(2nd-order method)with macro-stress and macrostrain as inputs.

whereVRVEis the volume of the RVE;neintis the number of the integration points in the elemente(with the volume ofis the von Mises equivalent stress at the Gauss point yI;IVOL(yI)is the volume of the integration point positioned at yI. Analogously, the volumetric averages of the 1storder and 2nd-order moments of the matrix stress are computed as

Fig. 4 Uniaxial tensile and shear EPBs of the composites with v1 of 0.20 and 0.50 simulated by MT, DI and MT-DI models.

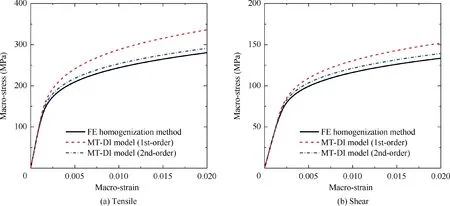
Fig. 5 Uniaxial tensile and shear EPBs of the composites predicted using MT-DI model and FE homogenization method.

Fig.6 Biaxial tensile and tensile/shear EPBs of the composites predicted using MT-DI model with 2nd-order secant formulation and FE homogenization method.

Regarding the mean-field homogenization models, the agreement of the predictions of the EPBs at the composite level does not guarantee that the stress and strain fields at the phase level can also be accurately computed. The average stresses and strains of the matrix and inclusions predicted by using the MT-DI model and the FE homogenization method are illustrated in Figs. 8 and 9. Fig. 8 indicates that the average stresses of the matrix obtained by the FE homogenization method agree well with those obtained by the MT-DI model with the 2nd-order secant formulation and deviate from those obtained by the MT-DI model with the 1st-order secant formulation,and the average strains of the matrix predicted using the MT-DI model with the 1st-order and 2nd-order secant formulations and the FE homogenization method are identical.For the inclusions (see Fig. 9), the predictions of the FE homogenization method are closer to those of the MT-DI model with the 2nd-order secant formulation than the 1storder secant formulation. Therefore, the MT-DI model with the 2nd-order secant formulation provides the more accurate predictions of the EPBs of the composites than the MT-DI model with the 1st-order secant formulation, as aforementioned.

The variation of the matrix average plastic strain regarding the macro-strain for the uniaxial tensile and shear loading conditions is plotted in Fig. 10. The MT-DI model and the FE homogenization method give the identical predictions of the average plastic strains of the matrix. Fig. 11 presents the matrix equivalent plastic strain, and shows that the difference of the predictions of the FE homogenization method and the MT-DI model is significant. Both the phenomena stem from the fact that the MT-DI model cannot adequately simulate the strain localization in the matrix,while the FE homogenization method can provide the local strain field of the matrix,as shown in Fig. 12.

The equivalent stress of the matrix and inclusions are given in Figs.13 and 14.It reveals that the predictions of the matrix provided by the FE homogenization method are close to those of the MT-DI model, while the predictions of the inclusions provided by the FE homogenization method are quite different from those of the MT-DI model, especially for the MT-DI model with the 1st-order secant formulation. In conclusion,the MT-DI model is capable of predicting the accurate EPBs of the composites,but not the same accurate EPBs for the constituents of the composites. Nevertheless, this can be relieved to a certain extent by using the 2nd-order secant formulation.

Fig. 8 Predicted average stresses and strains of the matrix using MT-DI model and FE homogenization method.

6. Conclusions

In this work, an interpolative MT-DI model with the secant formulation method is developed to predict the EPBs of aligned ellipsoidal inclusions composites, based on the wellestablished MT and DI models.The numerical implementation algorithms of the MT-DI model with the secant formulation using the macro-stress and macro-strain as inputs are detailed,respectively. The FE homogenization method is employed to provide the ‘‘exact” EPBs of the composites, and thus to validate the MT-DI model with the secant formulation. The following conclusions can be drawn:

Fig. 11 Evolution of equivalent plastic strain in the matrix as a function of applied strain predicted using MT-DI model and FE homogenization method.

Fig. 12 Total strain and plastic strain fields of the matrix predicted by FE homogenization method.

Fig. 13 Matrix equivalent stresses regarding macro-strain predicted using MT-DI model and FE homogenization method.

Fig. 14 Equivalent stresses of the inclusions regarding macro-strain predicted using MT-DI model and FE homogenization method.

(1) Compared with the results of the FE homogenization method, the MT-DI model with the 2nd-order secant formulation is validated to accurately predict the EPBs of composites.

(2) The MT-DI model with the secant formulation implemented by using the macro-stress and macro-strain as inputs gives the identical estimations of the EPBs of composites.

(3) The MT-DI model with the 2nd-order secant formulation predicts the more accurate EPBs of composites than the MT-DI model with the 1st-order secant formulation.

(4) The MT-DI model gives the accurate predictions of the EPBs of composites but does not give the accurate predictions for the matrix and inclusions.

Acknowledgements

The authors acknowledge the financial support from the Natural Science Basic Research Program of Shaanxi(No.2019JQ-857), the Doctoral Scientific Research Foundation of Xi’an Polytechnic University (No. BS201863), the China Textile Industry Federation Science and Technology Guidance Project(No. 2019002), and the Tianyuan Open Fund Project (No.tywl2019-14).

Appendix A. Determination of 2nd-order von Mises equivalent stress

Appendix A.1. Secant stiffness tensor method

Then, the required derivation can be computed from Eqs.(A.5)-(A.12). Consequently, the 2nd-order equivalent stress in the matrix (Eq. (A.13)) is computed by combining all the expressions sequentially.