Application of complex nonlinear modes to determine dry whip motion in a rubbing rotor system

Pingcho YU, Ynhong MA, Jie HONG, Guo CHEN

a College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China

b School of Energy and Power Engineering, Beihang University, Beijing 100083, China

c Collaborative Innovation Center of Advanced Aero-Engine, Beihang University, Beijing 100083, China

KEYWORDS Complex nonlinear mode;Dry whip;Existence boundary;Response characteristics

Abstract Dry whip motion is an instability of rubbing rotor system and may cause catastrophic failures of rotating machinery. Up to now, the related mechanisms of the dry whip is still not well understood.This paper aims to build the relationship between the complex nonlinear modes and the dry whip motion,and propose an effective method to predict the response characteristics and existence boundary of the dry whip through complex nonlinear modes.For the first time,the paper discusses how to use the complex nonlinear modes to predict the dry whip systematically, and as a consequence, the mechanism of the relationship between the complex nonlinear mode and the dry whip is revealed.The results show that the Backward Whirl(BW)mode motion of the rubbing rotor system dominates the response characteristics and the existence boundary of dry whip. The whirl amplitude and whirl frequency of dry whip are equal to the modal amplitude and modal frequency of the BW mode at the jump up point where the modal damping is equal to zero.The existence boundary corresponds to the critical rotation speed where the minimum of the modal damping of the BW mode motion is exactly equal to zero.Moreover,the proposed nonlinear modal method in this article is very effective for the prediction of dry whip of the more complicated practical rotor system, which has been verified by applying the predicted method into a rubbing rotor test rig.

1. Introduction

The rub-impact between rotor and stator is a common phenomenon in rotating machinery such as aero-engines and ground gas turbine plants.It can introduce high impact forces and friction effect into rotor system,which may result in severe vibration and even catastrophic failures in the worst case scenario.1-3During the past decades, a significant amount of researches have been done on the mechanisms and the complicated phenomena of rub-impact. These studies include the thermal effects,4-6the possible dynamic behaviors and corresponding response characteristics,7-9the constraint effects,10as well as dry-whip and its stability.11,12Among the different dynamic responses of the rubbing rotor, the dry whip is the most destructive motion to rotating machinery. During dry whip, the rotor undertakes very large deformation and is subjected to high-frequency stress,which will initiate the break or the fatigue damage of the shaft and cause the failure of the machine.13

A lot of scholars have been dedicated to the characteristics of dry whip,and the determination of the exist condition of the dry whip is an important research topic. The exist condition gives the boundaries by which the dry whip starts to exist.Black14developed a general model to investigate dry-friction backward whirl.He concluded that dry-friction whirl was only possible in the frequency band, extending from an individual rotor/stator natural frequency to the next higher combined system frequency. Zhang15extended the Black’s model to a rotor with a long-cantilevered disk,and gave a stability condition for the onset of back whirl in the form of a critical initial backward speed. Lingener16and Crandall17revisited the work of Black, and found a good correspondence between the derived condition and the experimental one in the case of small ratios of rotor radius to radial clearance.Bartha18did in a similar way to determine the critical impact velocity through simulations and tests. However, he concluded that Black’s whirl model may predict erroneous whirl ranges when applied to his experimental apparatus. Following the work of Black and Bartha, Childs and Bhattacharya19performed the numerical and experimental analysis on the dry whip and pointed out that the accurate whirl-range predictions require an accurate rotor-stator model, which can include multiple modes of the rotor/stator system. Therefore, a more accurate simulation model using beam finite element method to consider multimode was constructed to investigate the multimode dry whip characteristics,and the simulation results were validated effective by comparing with experimental data.20Furthermore,Childs and Kumar21presented a new rotor-stator model with considering the rubbing contact at two locations and developed the analytical solutions of dry whip and dry whirl.

Besides the exist boundary, another emphasis of the researches is the global responses of the rubbing rotor and the onset condition of the dry whip with imbalance.The onset condition is the boundary where dry whip can be directly triggered by imbalance.13At these aspects, Jiang did a lot of researches using the analytical method. For example, he built a rotor/stator rubbing model with the stator being modeled as an added stiffness. Based on the model, the physical reason for the onset of dry whip with imbalance was revealed, meanwhile the onset boundary of dry whip with imbalance was derived through the multiple scale method.13Then he proposed an analytical method to determine the global response characteristics of the above model and gained five types of the coexistences of the different rotor responses.22Moreover,the dynamic behavior and response boundary of the more complicated rotor/stator models, which consider the inertial motion of the stator and the cross-coupling stiffness, were investigated through the analytical and numerical methods11,23,24.

From the literatures described above,there have made great progress in the response characteristics of dry whip through numerical method or experiment method. However, the main drawback of the numerical and experiment methods is that a lot work is inevitable in order to determine the boundary of dry whip. In addition, as other rubbing responses may coexist with the dry whip motion at certain parameter regions, sometimes it’s not easy to obtain the dry whip response using simulation or experiment. To overcome these problems, Jiang did lots of work using analytical tools,22-24but his analytical method is mainly limited to two or four Degree-of-Freedom(DoF)rubbing systems and is difficult to extend to more complex rotor system.In recent work25we found that the instability of complex nonlinear modes is the inherent reason of dry whip.This discovery motivates us to think about if we can predict the response of dry whip from the point of nonlinear mode view.

This paper attempts to build the relationship between the complex nonlinear modes and the dry whip motion, and then to investigate how to predict the response characteristics and existence boundary of the dry whip through complex nonlinear modes. The main advantage of the proposed nonlinear modal method used to predict the dry whip is that it deals only with the so-called free vibration,which are more convenient in comparison with analyzing the nonlinear excited vibration. More importantly, we verify that the proposed prediction methods in this paper are also suitable for complex rotor system with a large number of DoFs. The paper is organized as follows:in Section 2 the mathematical model of a rubbing rotor system and its non-dimensional form are presented.In Sections 3 and 4, the relationship between nonlinear modes and dry whip motions are discussed,and the methods using complex nonlinear modes to predict dry whip motions are proposed. In Section 5, the proposed methods are applied to predict the response characteristics and existence boundary of dry whip of a test rotor to verify its effectiveness.

Fig. 1 Schematic representation of a Jeffcott rotor with a circular rigid stator.

2. Mathematical model

In this paper,we first use a simple rubbing rotor system to discuss the relationship between the nonlinear modes and dry whip motion, and to demonstrate how to apply complex nonlinear modes to predict dry whip motion.As shown in Fig.1,the rubbing rotor system consists of a Jeffcott rotor and a stator,which is modeled with an added stiffness.This model is widely used in the mechanism study of the rotor dynamics10,11,26due to its simplicity and its ability to reveal the basic mechanical characteristics. Although this model has only one node, with two degrees of translational freedom(one for each radial direction),it may exhibit a rich variety of phenomena,due to the presence of nonlinearities.The rotor has a massless shaft carrying a midspan disk with massm.The mass center of the rotor is located at a distanceefrom its geometrical center.The stiffness of shaft isk.The rotation speed of the rotor is ω-.The stator has a rigid ring with mass neglected.The rigid ring is supported elastically,the stiffness of the support iskc, and the damping is ignored. The clearance between the rotor and the stator isr0.

The governing equations of the above rotor/stator system can be written as follows,

The prime indicates the differentiation with respect to the new time scale τ.

3. Prediction method of the response characteristics of dry whip

3.1. Complex nonlinear modal characteristics of the rubbing rotor system

Based on the definition of complex modes for linear systems and the definition of nonlinear normal modes given by Rosenberg27and Shaw28et al., Laxalde and Thouverez29built the complex nonlinear modes concept. These complex nonlinear modes are actually an extension of the nonlinear normal modes and the linear complex modes, and the definition is a periodic or pseudo-periodic oscillation of the autonomous system with a phase difference between its degrees of freedom.Based on this definition, the solution method of the complex nonlinear modes is established based on the harmonic balance method.The basic process is given in Appendix of this article.First, we must discuss the nonlinear modal characteristics of the rubbing rotor system, as it is the basis on which the relationship between nonlinear modes and dry whip is built.

Ignoring the unbalance excitation term on the right side of the Eq. (4), the modal characteristics are calculated using the solution method in Appendix. The calculation parameters are as follows: ξ = 0.05, γ = 0.04,R0=1.05, μ=0.2,Rdisk=20R0,Ω=0.2,the number of harmonic termskis chosen as 3.

Fig.2 shows the motion orbits of the Forward Whirl(FW)and Backward Whirl (BW) mode motions of the rubbing rotor. Since the orbits of the mode motions at each modal amplitude are all similar, only mode motions with modal amplitude being 4 are presented as an example. The results show that the mode motion of the rubbing rotor system is a plane motion, which is distinct with the mode motion of the general vibration system. The orbits of the mode motions are all circular with two possible whirl direction, i.e. FW and BW. Besides, the calculation results listed in Table 1 reflect that the amplitude of the harmonic term withk>2 is less than that of the harmonic term withk=1 for both FW and BW mode motions, which indicates only fundamental component exists in the frequency domain of the mode motion. As a consequence, it is concluded that harmonic termk=1 being retained is sufficient in the calculation of the nonlinear modes for the rubbing rotor.

The modal frequency and modal damping of the FW and BW mode motions are extracted into Fig. 3. Several phenomena are obtained:

(1) At any certain modal amplitude, the magnitudes of the modal frequencies for FW mode motion and BW mode motion are identical, and only their symbols which represent whirl directions are opposite. When the modal amplitude is less than the rotor-to-stator clearance, the modal frequencies are equal to those of the linear rotor system without rubbing. Once the modal amplitude exceeds the clearance,both the magnitudes of modal frequencies increase with the increase of the modal amplitude. The reason is that the stiffness of the rotor system enhances due to the additional constraint caused by rubbing. Moreover, one can see that the magnitude of the modal frequency is at the range of [0.2, 1.01],the minimum of the modal frequency is equal to the modal frequency of the linear rotor system without rubbing, while the maximum of the modal frequency is approximately equal to the modal frequency of the linear rotor/stator system. The linear rotor/stator system refers to the dynamical system in which rotor touches the stator through the linear stiffnesskcand the friction at the contact point is ignored. The magnitudes of the modal frequencies for the linear rotor/stator system are about 1.02, which are approximately equal to the results shown in Fig. 3(a). Besides, the comparison with other parameters is also performed,as shown in Table 2,which indicates the correctness of above conclusion.Therefore, we concluded that the maximum of the modal frequency can be estimated by the linear rotor/stator system.

Fig. 2 Mode motions of rubbing rotor with modal amplitude being 4.

Table 1 Values of harmonic terms for mode shapes of rubbing rotor.

Fig. 3 Modal characteristics vs. modal amplitude for rubbing rotor.

Table 2 Comparison of modal frequency for rubbing system and linear rotor/stator system under different parameters.

(2) When no rubbing occurs,the modal damping is equal to original damping of the rotor system. Once the rubbing occurs,the modal damping starts to change.For the FW mode motion,the modal damping always increases with the increase of the modal amplitude. While the modal damping of the BW mode motion firstly decreases, then jump up to a positive value and increases with the increase of the modal amplitude. One can see that the modal damping of the FW mode motion is always greater than zero, while the modal damping of the BW mode motion may be less than zero.Therefore,it is summarized that the FW mode motion is stable all the time and the BW mode motion may be unstable under some certain modal amplitudes according to the stability condition given in Eq. (A7).

(3) The modal damping of the rubbing rotor system is closely related to the system’s original damping and the work done by the friction force. The related mechanism can be explained in terms of work done by friction force.The work done by friction force is Pr=-μsign（Vrel）ωFnR,whereFnis the rubbing normal force, μ is the friction coefficient, Vrel=ωR+ΩRdiskis the relative velocity at the rubbing point,Ris the whirl amplitude or the modal amplitude, ω is the whirl speed,and its value is equal to the modal angular frequency of the corresponding mode, the positive value means the mode is the forward whirl mode while the negative value means the mode is the backward whirl mode, Ω is the rotation speed. For the FW mode motion, the modal angular frequency ω is always greater than zero, then the relative velocity Vrel=ωR+ΩRdiskis also greater than zero,thusPris less than zero.That means the friction force always does negative work on the FW mode motion and dissipates energy of the rotor system, leading to the increase of the rotor’s modal damping. For the BW mode motion, the modal angular frequency ω is always less than zero. The relative velocity Vrel=ωR+ΩRdiskis greater than zero at lower modal amplitude, at that timePris greater than zero, meaning that the friction force does positive work on the BW mode motion and increases the energy of the rotor system, which is contrary to the case of FW mode motion and makes the modal damping reduce at that time. As the modal amplitude reaches the value that makeVrel<0,Prwill be less than zero,then the friction force does negative work on BW mode motion, thus the modal damping increases as the modal amplitude increases in that case.

3.2. Vibration response of the rubbing rotor system with unbalance excitation

Considering the unbalance excitation, simulations using Newmark method are run with a varying values of rotation speed.The rotor and rubbing parameters are same with those in Section 3.1.The results are shown in Fig.4.In the simulation,the initial conditions used at each step are given by the final steady-state solution of the previous one.Meanwhile sufficient time for each rotation speed Ω is calculated in order to reach the steady-state responses, and results of last fifty revolutions are saved. The simulations are performed twice. In the first round, simulations are made with progressively greater values of Ω, whereas in the second progressively smaller values of Ω are used.

The results in Fig. 4 can be summarized as follows:

(1) During the sweep-up, one can observe the response sequence of the rotor system is: no rub motion →full annular rub →partial rub →dry whip. No rub motion occurs when Ω<0.16. If Ω is at the region of 0.16-0.25, full annular rub will appear. For the partial rub,the region of Ω is 0.25-0.46. When Ω>0.46, the dry whip is generated. During the sweep-down, the rotor starts with no rub motion, then transfers into the dry whip at Ω≈0.86. The dry whip remains until a small value of Ω ≈0.04, where eccentricity suddenly drops leading to the no-rub motion.

(2) There are several coexistence regions of one more motion types. For example, full annular rub and dry whip coexist at the region of 0.16-0.25, whereas partial rub and dry whip coexist at the region of 0.25-0.46.Which kind of motion type occurs actually in the coexistence regions is depended on the external loadings and initial conditions of the rotor system. Besides, it should be noted that the dry whip can exist in a really large region of the rotation speed,and the region of dry whip for above parameters is Ω>0.04. The lowest rotation speed for the dry whip existing is called the existence condition of the dry whip, and the existence condition for above case is Ω=0.04.

Fig. 4 Response curve of rubbing rotor obtained by numerical integration.

Fig. 5 shows the response characteristics of the dry whip with Ω=0.46. It can be seen the rotor undertakes very large deformation which is far greater than rotor-to-stator clearance. Meanwhile, the frequency responses show that there exists a super-harmonic frequency content with very large amplitude. Moreover, the rotation frequent content can also be observed in the frequency response, however its amplitude is very little and can be ignored compared with the superharmonic frequency. Therefore, it can be inferred that the super-harmonic component dominates the motion of the rotor system with BW direction.

3.3. Prediction method of the response characteristics based on nonlinear modes

As the dry whip is dominated by the super-harmonic frequency content with BW direction, there might exist certain relationship between the dry whip and BW mode motion of the rubbing rotor. In order to study this problem, the response characteristics of the dry whip with different rotation speeds are firstly calculated using Newmark method,which are shown in

Fig. 5 Response characteristics of dry whip with Ω=0.46.

Fig. 6 Response characteristics of rubbing rotor with different rotation speeds.

Fig. 6. The calculation parameters are same with those in Section 3.2. It can be seen that the vibration amplitude and whirl frequency of the dry whip are about 4.6 and 0.143 respectively when Ω=0.2, while the vibration amplitude and whirl frequency increase slightly when Ω=0.3 and they are about 6.65 and 0.149 respectively.

The modal frequency and modal damping of the BW mode motion with the variation of the modal amplitude at above rotation speeds are also calculated based on the method in Section 3.1,as shown in Fig.7.The results show that the range of modal amplitude with β<0 increases with the increase of the rotation speeds, while the modal frequencies are not changed with the variation of rotation speeds. In addition, the modal characteristics at different modal amplitudes are distinct, indicating the energy dependence or amplitude dependence of the complex nonlinear modes of the rubbing rotor.

Using the vibration amplitudes of the dry whip at these rotation speeds (Fig. 6), the modal frequency and modal damping of the rubbing rotor system with certain dry whip motion can also be obtained, which are marked with point‘‘A”and‘‘B”in Fig.7.Meanwhile,the response characteristics of dry whip and corresponding modal characteristics are also extracted in Table 3. One can observe that the magnitudes of modal damping under these vibration amplitudes are approximately equal to zero (Fig. 7(a)), meanwhile the modal frequencies are identical to the whirl frequencies of the dry whip.Therefore,it is inferred that the main frequency content of the dry whip is the BW mode motion of the rubbing rotor system under the corresponding vibration amplitude. That means the BW mode motion of the rubbing rotor system dominates the dry whip.

Since the dry whip of the rubbing rotor system is dependent on the BW mode motion, we can infer that the response characteristics of the dry whip could be predicted by the BW mode motion. In fact, Fig. 7(a) indicates that the average amplitude of the dry whip at a certain rotation speed just corresponds to the modal amplitude at the jump up point with the modal damping being approximately zero under this rotation speed.Meanwhile, the whirl frequency of the dry whip can be obtained according to the modal frequency curve and the modal amplitude at the jump up point. Taking the case of Ω=0.2 as an example, a qualitative explanation is given to validate this conclusion from the view point of stability of the BW mode motion. Three kinds of cases are considered in the following analysis:

Case 1: Assume that the amplitude of the dry whip is at point ‘‘C” (Fig. 7(a)) where the modal damping is less than zero, then the BW mode motion here is not stable, consequently the amplitude of the dry whip will increase until the amplitude reaches the jump up point ‘‘A”. The BW mode motion which dominates the dry whip will maintain a kind of dynamical stability at neighborhood of the jump up point‘‘A”,i.e.if the amplitude exceeds the modal amplitude at point‘‘A”,the modal damping β>0 and the motion amplitude will decrease with the effect of the damping dissipation until β reaches 0, while if the amplitude is slightly lower than the modal amplitude at point‘‘A”,then the motion amplitude will increase because of the instability until β also reaches 0.

Case 2: If the amplitude of the dry whip is at point ‘‘D”(Fig. 7(a)) where the modal damping is greater than zero, the amplitude of the dry whip will decrease because of the damping dissipation until the amplitude reaches the jump point‘‘A”.Then BW mode motion will maintain the dynamical stability as described in the Case 1.

Fig. 7 BW modal characteristics of the rubbing rotor with different rotation speeds.

Table 3 Modal characteristics and response characteristics of rubbing rotor with different rotation speeds.

Case 3: If the amplitude of the dry whip is at point ‘‘E”where the modal damping is also greater than zero,the amplitude of the dry whip will decrease until the amplitude reaches zero, which is different with the Case 2. That means the dry whip cannot happen in this case.

The above analysis indicates that the dry whip with amplitude being unequal to that at the jump up point may be unstable (Case 1 and Case 2) or cannot appear (Case 3). The stable dry whip can only happen with the amplitude being at the jump up point where β ≈0.Therefore,the amplitude and whirl frequency of the dry whip at a certain rotation speed can be determined only through the calculation of modal characteristics under this rotation speed, and response calculation of the dry whip by time-consuming numerical method is no longer needed.

In addition, the results in Table 3 also show that as the rotation speeds increase, the whirl amplitudes increase significantly,and the whirl frequencies of dry whip also increase,but the variation is very little.

According to above analysis, the prediction method of the response characteristics of the dry whip based on complex nonlinear modes is proposed, and its basic process is shown in Fig. 8:

Step 1. For certain rotation speed, the curves of modal damping and modal frequency vs. the modal amplitude are calculated based on the solution method in Appendix.

Fig.8 Process of prediction method for response characteristics of dry whip based on complex nonlinear modes.

Step 2. The amplitude corresponding to the jump point of modal damping is extracted according to the curve of modal damping vs. the modal amplitude, and this value is approximately equal to the amplitude of dry whip.

Step 3. The modal frequency corresponding the amplitude obtain in Step 2 is extracted according to the curve of modal frequency vs. the modal amplitude, and this value is the whirl frequency of dry whip.

Table 4 Modal characteristics of rubbing rotor at jump up point with different stiffness ratios.

Fig. 9 Influence of stiffness ratios on BW modal characteristics of the rubbing rotor.

3.4. Influence laws of the key parameters on response characteristics

The influence of rotor/stator stiffness ratios γ on the response characteristics of the dry whip is studied based on the proposed method in Section 3.3. The rotor/stator stiffness is defined as γ =k/kc, wherekis the rotor’s stiffness andkcis the stator’s stiffness. It reflects the strength of the additional constraint caused by rub-impact. Fig. 9 presents the modal damping and modal frequencies of the BW mode motion with different stiffness ratios,meanwhile the modal amplitudes and modal frequencies at the jump up point which represent the whirl amplitude and whirl frequencies of dry whip are extracted into Table 4. The rotation speed in the calculation is 0.3, the stiffness ratios are 0.04, 0.20 and 0.40 respectively,and the other parameters are same with those in Section 3.2.

The results show that the magnitudes of modal frequency increase, whereas the magnitudes of the modal damping decrease as the stiffness ratio increases. Meanwhile the region of modal amplitude with β<0 decreases with the increase of stiffness ratio.Moreover,according to the results in Table 4,it can be seen that the modal amplitudes at the jump up point decrease and the modal frequencies at the jump up point increase with the increase of stiffness ratio.This indicates when the stiffness ratio enhances, the whirl amplitudes of dry whip will decrease whereas the whirl frequencies will increase.

Fig. 10 and Table 5 exhibit the influence of friction coefficients on the modal characteristics of the BW mode motions.The friction coefficients are 0.15, 0.30 and 0.50 respectively,the rotation speed is 0.3, and the other parameters are also used those in Section 3.2.The results show that the magnitudes of the modal damping increase significantly with the increase of friction coefficient. However, the modal frequencies under different friction coefficients are nearly identical, which indicates the influence of friction coefficients on modal frequencies is little.Besides,one can note that the modal amplitudes at the jump up point with different friction coefficients are also very identical, the modal frequencies increase slightly with the increase of friction coefficients but the change is extremely limited. Therefore, it is concluded that the whirl amplitude and whirl frequencies of the dry whip are almost unchanged with the variation of friction coefficient.

4. Prediction method of the existence boundary of dry whip

The analysis in Section 3.3 shows that the dry whip is dominated by the BW mode motion whose modal amplitude is corresponding to the jump up point of the modal damping curve and modal damping is about zero. It means that the dry whip cannot appear if the region of β<0 does not exist.Therefore,it is inferred that the existence boundary of the dry whip corresponds to the critical rotation speed where the minimum of the modal damping of the BW mode motion is exactly equal to zero,such as the blue curve in Fig.11.The qualitative analysis with three cases is given to explain the conclusion using the modal results shown in Fig. 11.

Case 1 with Ω=0.02:Fig.11 shows that the modal damping under any modal amplitude is greater than zero, meaning that the BW mode motion with any modal amplitude will attenuates to zero, consequently dry whip cannot exist in this case.

Case 2 with Ω=0.20: It can be seen that there exists the region with β<0. As described in Section 4.2, a stable dry whip can happen at the jump up pointCwhen the original vibration amplitude is higher than the modal amplitude of pointB.

Case 3 with Ω=0.04:The minimum of the modal damping in that case is exactly equal to zero.If the rotation speed is disturbed and slightly greater than 0.04, then the region with β<0 appears and dry whip can happen as described in Case 2.While if the rotation speed is less than 0.04,then the modal damping will be always greater than zero and dry whip cannot happen as described in Case 1.

Table 5 Modal characteristics of rubbing rotor at jump up point with different friction coefficients.

Fig. 10 Influence of friction coefficients on BW modal characteristics of the rubbing rotor.

Fig. 11 Modal damping of BW mode motion with different rotation speeds.

According to above analysis, the prediction method of the existence boundary of the dry whip based on complex nonlinear modes is proposed, as shown in Fig. 12. The main idea of this method is to seek the critical rotation speed where the minimum of the modal damping of the BW mode motion is exactly equal to zero. Firstly, given a large enough rotation speed region[Ω1,Ωu],and make sure that the minimum of the modal damping (βmin) with rotation speed Ω1is greater than zero,while the minimum of the modal damping with rotation speed Ωuis less than zero. Secondly, using the bisection search method to narrow the rotation speed region until finding the critical rotation speed where the minimum of the modal damping of the BW mode motion is exactly equal to zero, this critical speed corresponds to the boundaries by which the dry whip starts to exist.

In order to validate above predicted method, the existence boundaries of the dry whip with different stiffness ratios γ are determined by the complex nonlinear modes and numerical simulations respectively. Fig. 13(a) presents the modal damping curves with different stiffness ratios, and the rotation speeds under which the minimum of modal damping is exactly equal to zero are marked in the figure and listed in Table 6.Fig. 13(b) shows the response curves of the rubbing rotor system with different stiffness ratios,and the existence boundaries of the dry whip are also marked and listed in Table 6.One can observe that the existence boundaries obtained by the complex nonlinear modes are consistent with those of the numerical results, which proves the efficiency of the complex nonlinear modes to predict the existence boundary of dry whip.

Based on the proposed prediction method of complex nonlinear method,the existence boundaries of dry whip under different stiffness ratio and friction coefficient are obtained, as shown in Fig. 14. One can see that the existence boundaries of dry whip increase with the increasing stiffness ratio and the decreasing friction coefficient, which means decreasing the friction coefficient or increasing the stiffness ratio may improve the stability of the rotor system.

Fig. 12 Process of prediction method for existence boundary of dry whip based on complex nonlinear modes.

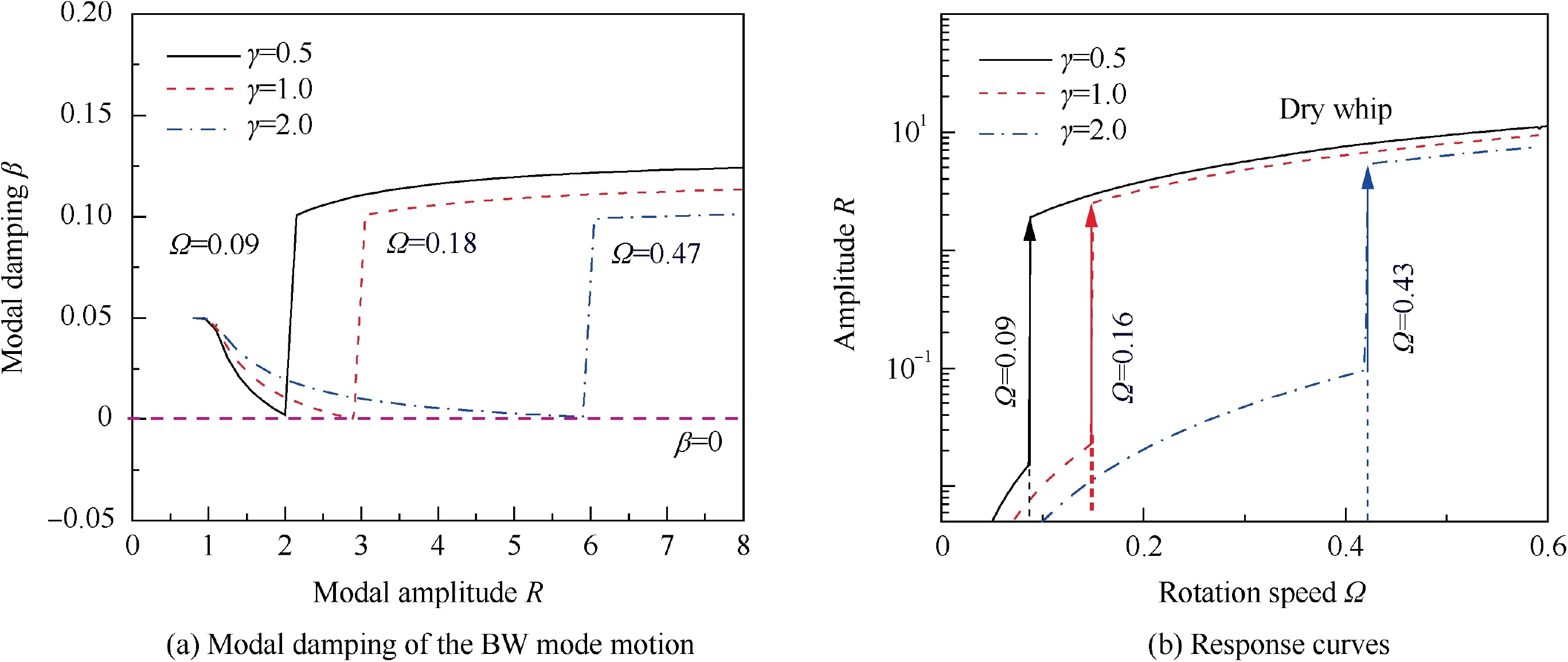
Fig. 13 Comparison of mode and response results for rubbing rotor with different stiffness ratios.

Table 6 Comparison of existence boundary obtained by numerical simulation and complex nonlinear modes.

5. Verification of the theoretical analysis based on experiment

Above sections present the methods those are used to predict the response characteristics and existence boundary of the dry whip. In this section, the proposed methods are applied for the prediction of the dry whip of a rubbing rotor test rig in Refs. 30,31. The comparison between the theoretical result and experiment result is performed to verify the effectiveness of the proposed method. One important point that we must highlight is that the rotor test rig belongs to a complex system with lots of DoFs, which shows that our proposed method is not limited to the simple system in Fig. 1.

5.1. Overview of the test rig

Fig. 15 shows the test rig designed by Yu and Muszynska et al.30,31The test rig is mainly used to study the full annular rub. A shaft with the diameter and length of 0.01 m and 0.56 m, respectively, is supported by two brass bushing bearings and driven by a 75 W motor. One or two disks were attached to the shaft in the midspan. A seal was located at the outboard side of the shaft. The seals used in the experiments were either tightly or flexibly fitted with an ‘‘O-ring’’in the seal support. The rotor was originally centered in the seal and well balanced. A known mass unbalance was then added to one of the disks at the radius of 0.03 m.

Four transducers are displaced along the axial position of the rotor shaft and are utilized to measure the orbit of the rotor.Transducers 1 and 2 are located near the seal,and transducers 3 and 4 are close to the rotor midspan.In addition,one speed transducer and one Keyphasor® transducer are applied for the speed and phase measurement.

Fig. 14 Existence boundary of dry whip with variation of key parameters.

Fig. 15 Rotor/seal full annular rubbing test rig.

5.2. Modeling of the test rig

5.2.1. Identification of the rotor parameters

The structure of above rubbing rotor system is shown in Fig. 16. Parameters including the length and the diameter of the shaft are marked in the figure. The support stiffnessk1andk2are equal to 1.75×105N/m. These parameters are found directly in Ref. 31.

Finite Element Method(FEM)is used to get the dynamical equation of the rotor system. The shaft is modelled by the beam element. The disk is modelled by the mass element.The support is modelled by the spring element.The dynamical matrix of the mass element, beam element and spring element can be referred to 32. The final dynamic model we built consists 8 nodes and 32 DoFs, as shown in Fig. 17. For this FE model, the mass of the disk and the damping of the system should be identified according to the experimental results,because these two parameters are not given in the reference.Fig. 18(a) exhibits experimental results about the vibration amplitude vs. the rotation speed during the start-up and shut down process of the rotor. The 1.1 g of unbalance mass is applied to the disk. According to the resonance speed (1460-1490 r/min)shown in experimental result,the mass of the disk is identified,which is 1.17 kg.Meantime,the damping ratio of the rotor system is identified through the half-power method,which is 0.011. The final parameters of the rotor system is shown in Table 7.Simulation of the unbalance response is performed based on the FE model and the parameters shown in Table 7. The simulated result is exhibited in Fig. 18(b). As we can see, the simulated result is good agreement with the experimental result,indicating that the correctness of the given rotor parameters.

Fig. 16 Structural sketch of rubbing rotor system.

Fig. 17 Finite element sketch of rotor system.

Fig. 18 Comparison of experimental and simulated results (1 mils=25.4 um).

5.2.2. Identification of the rubbing parameters

In addition to the rotor parameters, the rubbing parameters such as the rubbing stiffness, friction coefficient and the clearance ratio (C/R,Cis the rotor-to-stator clearance,Ris the radius of the rotor at the contact point)also need to be known.The above rubbing parameters are also identified according to the rubbing experimental results. Fig. 19 shows experimental results about the vibration amplitude of the rotor system during the start-up process when the rotor/seal rub-impact occurs.The rotor orbits at several rotation speeds are also given in the figure. Meantime, the corresponding frequency components are shown in Fig.20,which is directly obtained in the Ref.31.The experimental results show that the rotor starts to rub with seal at about 1500 r/min. At that time, the rotor is in the condition of partial rubbing with forward whirl direction.When the rotation speed is 1550-1650 r/min, the whirl direction changes and the rotor is in the state of partial rubbing with backward whirl direction. When the rotation speed reaches 1700 r/min, the backward whirl full annular rubbing(dry whip) appears, and the whirl frequency is about 38.3 Hz. After that, the whirl frequency hardly change with the increase of the rotation speed, and the rotor is always in the state of the dry whip motion (see Fig. 20).

Fig.19 Vibration amplitude of rotor during start-up process when rub-impact occurs,result is given in Ref.31,unbalance mass is 0.5 g.

Fig. 20 Spectrum cascade of rotor vibration response during start-up process when rub-impact occurs, result is given in Ref.31.

Fig. 21 Simulated vibration amplitude during start-up process using above rubbing parameters and rotor parameters.

Table 8 Identified rubbing parameters.

According to above experimental results, the rubbing parameters are identified through lots of numerical simulations, which can be seen in Table 8. Based on above identified rubbing parameters and rotor parameters, the vibration response of the rotor system with rub-impact is simulated through Newmark method, as shown in Figs. 21 and 22.Fig.21 presents curves of the vibration amplitude vs.the rotation speed, and Fig. 22 presents the response in frequency domain of dry whip motion. From the simulated results, the vibration amplitude at different rotation speeds, the whirl frequency in the case of dry whip motion, the rotation speeds under which the rub-impact begin to appear and the dry whip motion begin to appear are all coincident with the experimental results, which shows the correctness of the rubbing parameters and rotor parameters.

Fig. 22 Simulated response in frequency domain when rotation speed is 1700 r/min.

Fig. 23 Backward whirl mode of the test rotor with rub-impact.

Table 9 Response characteristics of dry whip obtained by theoretical prediction and experiment.

5.3. Comparison of the theoretical prediction and the experimental result

The predicted method for the response characteristics of the dry whip is firstly verified. Based on the FE model and the identified system parameters, the backward whirl modal frequency and modal damping at different rotation speeds are calculated through solution method in Section 3, as shown in Fig. 23. Then the whirl frequencies and whirl amplitudes at these rotation speeds can be obtained, which are listed in Table 9. Meantime, the experimental results for the whirl amplitudes at these rotation speeds are also can be obtained through Fig. 19, which are also listed in Table 9. It should be noted that the experimental results about the whirl frequencies cannot be obtained precisely.Ref.31 only pointed out that the whirl frequencies of the dry whip motion are nearly equal to 38.3 Hz, therefore we assumed that the whirl frequencies at these rotation speeds are basically equal to 38.3 Hz.

According to the results in Table 9, following conclusions can be drawn:①The whirl amplitudes of the dry whip motion increase with the increase of the rotation speeds, and the predicted values at these rotation speeds are nearly equal to values of the experimental results.②The whirl frequencies predicted by the proposed method is about 38-39 Hz at these rotation speeds,while the experimental results about the whirl frequencies are about 38.3 Hz. As we can see, the predicted results about the whirl frequency are also coincident with the experimental results. Therefore, we can conclude that the proposed method is effective in the prediction of the response characteristics of the dry whip motion.

Furthermore, the predicted method for the existence boundary of the dry whip is verified. Fig. 24 shows the backward whirl modal damping of the rotor system when rotation speeds are 100-500 r/min. According the conclusion in Section 5 that the existence boundary of the dry whip corresponds to the critical rotation speed where the minimum of the modal damping of the BW mode motion is exactly equal to zero,we can predict that the rotation speed under which dry whip can appear is at the region of 100-300 r/min. Fig. 25 shows the experimental results of the rotor system during the start-up/run-down processes. It can be seen that the rotor keeps the state of dry whip during run-down process until the rotation speed decrease to about 150 r/min,which indicates that the existence boundary of the dry whip obtained by experiment is about 150 r/min. By comparing the predicted result and the experimental result about the existence boundary of the dry whip motion, we can see that they are coincident.Therefore, it is concluded that the proposed method is also effective in the prediction of the response characteristics of the dry whip motion.

Fig. 24 Curves of backward whirl modal damping at different rotation speeds.

Fig. 25 Spectrum cascade of the rotor system during start-up/rundown processes, results in Ref. 30.

6. Conclusions

The article demonstrates how to use the complex nonlinear modes to predict the response characteristics and the existence boundary for the dry whip systematically. From the point of response view, the response of dry whip for the rubbing rotor mainly consists of BW mode motion.The BW mode motion at the jump point where the modal damping is zero dominates the dry whip, and can be used to predict the response characteristics of dry whip. The whirl amplitude and whirl frequency of the dry whip are approximately equal to the modal amplitude and modal frequency of the BW mode motion at the jump up point.Both the rotation speed and stiffness ratio have a significant influence on the whirl amplitude and whirl frequency of the dry whip, however the friction coefficient does not. From the point of modal view, the existence boundary of the dry whip can also be predicted by the BW mode. It corresponds to the critical rotation speed where the minimum of the modal damping for the BW mode is exactly equal to zero.The critical speed for the existence boundary of dry whip increases for the increasing of the stiffness ratio and the decreasing of the friction coefficient.

Based on the test rig of a rotor/seal rubbing system in Refs.30,31,the verification of the proposed method for predicting the existence boundary and response characteristics of the dry whip motion is performed. The comparison between the theoretical results and the experimental results show that the complex nonlinear modal analysis is very effective for the prediction of dry whip.As the proposed methods are based on the modal analysis,it only deals with the free vibration of the rubbing rotor system without excitation,the time-consuming nonlinear response calculation is no longer needed, therefore, it is more efficient and accurate. Moreover, the success of the proposed method in applying the test rig demonstrates that it is also suitable for complex rotor system with a large number of DoFs.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors would like to acknowledge the financial support from the National Natural Science Foundation of China(No.52005252),the Fundamental Research Funds for the Central Universities (No. NT2020018), and the National Science and Technology Major Project (2017-IV-0008-0045).

Appendix.Solution method of the complex nonlinear modes:

The motion equation of the general discrete, autonomous,non-conservative mechanical system is stated as follows:

where M、D、K denote the mass matrix,damping matrix and stiffness matrix respectively. g is the nonlinear force vector.

The complex nonlinear modes are actually an extension of the nonlinear normal modes and the linear complex modes.The definition of complex nonlinear mode is an periodic or pseudo-periodic oscillation of the autonomous system with a phase difference between its degrees of freedom. According to the definition, the complex nonlinear modes of Eq. (A1)are sought in the form of a decaying multi-harmonic form,given by the following equation:

The decay of the solution can be neglected during the periodTused in the projection as fully explained in Ref.33,which allows to use the orthogonality of the projection basis.Following complex algebraic equations are obtained according a subsequent Fourier-Galerkin projection procedure coupled through the projection of the nonlinear forces 〈g，ek〉,as shown in Eq. (A4).

Another problem is that the nonlinear rubbing forces are the explicit function of the displacement only in time domain.Therefore,the frequency-domain components of the nonlinear rubbing forces cannot be derived from the frequency-domain components of the displacement directly. An alternating frequency-time domain scheme is adopted to address this issue,33,34as shown in Eq. (A6). This method only requires to know the nonlinear law in the time domain, and the direct(FFT) and inverse (IFFT) Fourier transforms to determine〈g，ek〉 at each step of the solution.

Eventually,the nonlinear algebraic equations can be solved using the Newton method. As the method is a local convergence algorithm,the initial value is very important and chosen as the eigen-solution of the corresponding linear system without rub-impact in this paper. In addition, since the Newton method only handles real arithmetics, the actual variables of the problem are the real and imaginary parts of the unknownssolved is actually ∀k∈［1 ，l］:［Re（rk） lm（rk）］T=0, where rkis defined in Eq. (A4).

The stability of the nonlinear mode motion is determined by the real parts of the corresponding eigenvalues and its stable condition can be expressed as,