Reliability and global sensitivity analysis for an airplane slat mechanism considering wear degradation

Changcong ZHOU, Haodong ZHAO, Qi CHANG, Mengyao JI, Chen LI

Institute of Aircraft Reliability Engineering, Northwestern Polytechnical University, Xi’an, 710072, PR China

KEYWORDS Slat mechanism;Roller wheel;Wear degradation;Reliability;Sensitivity

Abstract This paper focuses on the issue of reliability and global sensitivity analysis for an airplane slat mechanism considering the uncertainties in the wear process of mechanical components.First,the multi-body kinematic model of the slat mechanism is built in the ADAMS software.The geometrical sizes of the roller wheels after wear degradation are considered as input variables and the angle the slat should turn is considered as the output response.To accurately identify the influential roller wheels to the reliability and robustness of the slat mechanism, the failure probability based sensitivity and variance-based sensitivity indices are introduced. Comprehensive analysis of the results have shown that the reliability analysis and global sensitivity theory can help engineers find significant parts by their contributions,thus provide guidance for mechanical design and maintenance.

1. Introduction

As one of the important devices in a civil airplane, the slat mechanism plays a crucial role in ensuring the flight safety.1The slat mechanism studied in this work is comprised by the airfoil, curved rail, rack, pinion, roller wheels and wing rib.During the stage of takeoff and landing, the slat mechanism is designed to function properly under complex environments,to provide extra lift for the airplane.In this process,the airfoil must be rotated to a specific position as required. Therefore,we must ensure that the angle error of the slat rotation is less than a permissible threshold.

However, extensive existence of uncertainties both in the environment and geometrical properties puts the reliability and robustness of the slat mechanism to harsh tests.2The situation can become more severe for civil commercial airplanes,of which the takeoff and landing are much more often than military airplanes.It is worth mentioning that the degradation of mechanism components is an important factor influencing the motion performance.3During the service of civil airplane,repeated external loads lead to the degradation of mechanism parts,such as wear of roller wheels,which may further result in malfunction of the whole mechanism. With this respect, it is meaningful to study the impacts of worn parts on the output performance of mechanisms, and take corresponding measures. For a simple planar mechanism, kinematic equations can be directly established to explicitly obtain the movement characteristics. However, for many complex mechanisms used in engineering, it is usually very difficult to get the explicit kinematic equations. In this work, the multi-body dynamical model of the slat mechanism is built in ADAMS, which is a commercial software for dynamical simulation, to simulate the mechanism performance and build the implicit relationship between model inputs and outputs.

Apart from considering the issue of mechanism reliability and robustness when uncertainties are involved, it is also meaningful to find out how the input uncertainties affect the output performance.This can be done by the so-called‘‘sensitivity analysis”.4Sensitivity is the science that studies how the uncertainty in the output can be apportioned to the inputs,and can be generalized into two categories: local sensitivity and global sensitivity.5Local sensitivity is mainly referring to the derivatives of output characteristics to input parameters, and global sensitivity studies the effect of the whole range of inputs. Global sensitivity analysis plays an important role in identifying and representing uncertainties in engineering. The last few decades have witnessed a rapid development of global sensitivity theory, and many researchers have proposed different sensitivity indices, as well as corresponding computing techniques.6,7Among these different indices, the variance based ones have attracted increasing interests as they are able to capture the influence of the full range of variation of each input factor, and reflect the interaction effects among input factors.8Furthermore,variance is a significant index of robustness. Those input parameters with great impacts on output variance are believed to have evident effects on the system robustness. Variance based sensitivity analysis has been acknowledged as a versatile and effective tool in the uncertainty analysis. In addition, failure probability based sensitivity index reflects the impact of the input variable uncertainty on the failure probability of the mechanism.9The global sensitivity ranking results can provide meaningful information for reliability design accurately. However, reliability and global sensitivity analysis requires thousands of model calls, which will result in a time-consuming calculation process, thus it is usually unacceptable for engineering applications. For relieving the computational cost, we introduce the surrogate model to approximate the relationship between the inputs and output for the slat mechanism.Artificial neural networks are designed by researchers from many scientific disciplines to solve a variety of problems in pattern recognition, prediction, optimization, etc.10Compared with other surrogate models, the artificial neural networks have shown many advantages both in accuracy and efficiency.

In this work,we focus on the function reliability of the slat mechanism with uncertain parameters and worn mechanical components. First, we establish the dynamic model of the slat mechanism in the ADAMS software, and then we introduce the Archard theory to describe the wear degradation process of roller wheels.11The variance based sensitivity index and failure probability based sensitivity index are then introduced to explore the impacts of input parameters on the output variance and failure probability of the slat mechanism respectively. To reduce the computational burden,the artificial neural network is employed to approximate the relationship between worn sizes of roller wheels and angle of slat rotation.Analysis results show that the global sensitivity does provide useful information for engineers.

The remainder of this paper is organized as follows. Section 2 introduces the slat mechanism and wear degradation process of roller wheels. Section 3 discusses the reliability and sensitivity model for the slat mechanism, of which the results are presented and discussed in Section 4.Section 5 gives conclusions.

2. The slat mechanism with wear of roller wheels

The slat mechanism studied in this work is shown in Fig. 1,which is built in ADAMS. It is comprised by airfoil, curved rails, racks, pinions, roller wheels and wing ribs. The roller wheels of the slat mechanism are designated byr1-r12. The driving force is delivered by the rack and pinion, and the trajectory is constrained by the slide and roller wheels. Whether the slat mechanism can function properly will directly affect the flight safety. During the repeated movements of the slat mechanism, the weight itself and aerodynamic loads could result in considerable pressure at the contact surface of roller wheels and slide. Compared with the material of slide, the material of roller wheels is more vulnerable to wear. Thus,how the worn roller wheels affect the performance of slat mechanism becomes the focus of this work.

During the stage of takeoff and landing of the civil airplane,the slat mechanism at the front of wing will undergo repeated extension and extraction. Due to the external aerodynamic load and self-weight,the stress at contact area of roller wheels and slide is often large,ultimately leading to wear of the roller wheels. At present, the Archard model is popular to estimate the wear extent, of which the formulation is shown as follows,11,12

whereVis the wear volume,Pis the normal pressure at the contact surface,Lis the relative slip distance,His the Brinell hardness of material,andKis the wear coefficient.The relative slip distance can be obtained by geometrical relationship as follows,

In Eqs (2) and (3),bandris the height and radius of the roller wheel respectively,r0is the radius of the slide, φ is the angle rotated by the slide,andnis the number of times of wear.

Combining Eqs. (1)-(3) the geometrical abrasion for the radius of the roller wheel by wear can be obtained as follows,

For convenience of description, the geometrical abrasions are designated byΔr1～Δr12. The wear coefficientKis set as 1.0×10-4. The angle φ is measured by ADAMS, which is 70 degree. Other wear parameters involved in Eq. (4) are considered to obey the normal distribution, with the distribution information listed in Table 1.

Generate the samples of wear parameters according to the distribution information,and obtain the samples of the normal pressurePthrough the ADAMS model. The relationship between wear timesnand vertical pressurePis built and shown in Table 2. Note that the vertical pressure measured in the roller wheel designated asr1,r3,r5,r7,r9,r11is rather small compared with the rest of roller wheels, thus we do not consider their wear abrasions, which is why only the pressure of roller wheel designated asr2,r4,r6,r8,r10,r12is shown in Table 2.By Table 2,the samples of Δr2,Δr4,Δr6,Δr8,Δr10,Δr12can be obtained through Eq. (4) at given value ofn, as long as the samples of the inputs are first obtained with the information in Table 1.

The purpose for the rest of this work is to study the reliability and sensitivity of the slat mechanism when considering the random uncertainties of these geometrical abrasions, i.e.Δr2, Δr4, Δr6, Δr8, Δr10, Δr12. Obviously, these geometrical abrasions are random variables, as they are the functions of the random wear parameters shown in Table 1. Samples of the geometrical abrasions can be obtained by a combination use of Tables 1 and 2 and Eq. (4) It should be noted that as long as their samples can be obtained, it is not necessary to get the exact probability distribution of Δr2, Δr4, Δr6, Δr8,Δr10,Δr12,as only the Monte Carlo simulation method is used in this work to estimate the reliability and sensitivity.The output response that we are interested in is the angle turned by the slat mechanism, which is denoted as θ.

Fig. 1 Dynamic model of slat mechanism.

Table 1 Distribution information of wear parameters.

Table 2 Linear regression function of vertical pressure on the roller wheels.

3. Reliability and sensitivity model of the slat mechanism

Mechanism safety mainly considers two aspects, one aspect is reliability and the other is sensitivity.13Reliability analysis aims at calculating the failure probability or reliability of the mechanism, while the sensitivity analysis aims at studying the influence of the distribution parameters or uncertainty of the input variables on the statistical characteristics of the output performance.One essential step of reliability design is sensitivity analysis, which gives the relative sensitivity of each input parameter that affects mechanism reliability.

Sensitivity analysis can be categorized into local sensitivity analysis and global sensitivity analysis.14Global sensitivity is also defined as importance measure in many literatures. Compared to local sensitivity analysis, global sensitivity provides a more comprehensive impact of input uncertainty on output performance. The most widely used ones are the variance based sensitivity index and failure probability based sensitivity index. The variance based sensitivity index reflects the effect of input uncertainty on the output variance, which can be used to measure the robustness of the output performance. At the same time, failure probability based sensitivity index reflects the impact of the input uncertainty on the failure probability of the mechanism. Both sensitivity indices fall in the common rationale defined by Borgonovo et al.7A detailed description of reliability analysis and the two global sensitivity indices for the slat mechanism are presented as follows.

3.1. Reliability analysis model for the slat mechanism

According to the discussion in Section 2, the relationship between input variables, i.e. the geometrical abrasions of six roller wheels, and output responses, i.e. the angle turned by the slat, can be expressed as follows,

whereθistheangleturnedbytheslat,Δrm（m=2，4，6，8，10，12） is the geometrical abrasions ofith roller wheel.

To avoid bewilderment in the following sections, we also useYto denote the output response, i.e. θ for the slat mechanism, andXito denote the input, i.e. Δrmfor the slat mechanism. Note thati=m/2, which means we are usingX1,X2,X3,X4,X5,X6to denote Δr2, Δr4, Δr6, Δr8, Δr10, Δr12, respectively.Thus,the input-output response function in Eq.(5)can be rewritten as

During the takeoff and landing stage of the airplane, the slat mechanism is designed to function properly under complex environments. For the function reliability of slat mechanism,we must ensure that the angle error of the slat rotation is less than a certain boundary value which is defined as failure threshold value. For the slat mechanism, the limit state function is defined as

where X =［X1，X2，X3，X4，X5，X6］T, ε is failure threshold value of slat mechanism, θ0is the design angle of the slat rotation.Failure threshold value represents the upper limit we can allow for the angle error of the slat rotation.A smaller failure threshold means a higher requirement for the accurate movement of the slat mechanism.Thus,the failure domain for the slat mechanism can be shown as,

Furthermore,the failure probability for the slat mechanism can be obtained as,

IF（X）is the indicator function of failure domain,fXdenotes the joint probability density function,Rdenotes the whole input space, andE［·］ is the expectation operator. According to the Monte Carlo method in reliability theory, we can use the expectation of the indication function to estimate the failure probability, which is

whereNis the number of total samples, andNfis the number of samples falling into the failure domain.

3.2. Variance based sensitivity index

For an input-output response function asY=h（X）, where X=［X1，X2，...，Xk］T, Sobol15proposed that it can always be decomposed into summands of different dimensions,which is

whereh0denotes the mean value ofh（X）. Global sensitivity based on variance is to quantify the contribution of an individual input variable to the output variance, and Sobol proposed the variance decomposition equation based on Eq. (12),

Viis the first order variance contribution ofXi,and can be formulated as

where X-idenotes the vector of all input variables exceptXi,i.e.X-i=［X1，...，Xi-1，Xi+1，...Xk］T.Vijand higher order variance terms in Eq. (13) denote the contribution to the output variance of variable interaction brought by the form of the response function.When only the first order variance contribution is considered,the variance decomposition can be reformulated as

The first order variance contributionViis also referred to as the main effect ofXion the output variance, and it measures the first order effect ofXion the output, ignoring the interactions betweenXiand the other variables. When taking the interactions into consideration, the total contribution ofXiis measured byEX-i（VXi（Y|X-i））. According to the known identity:

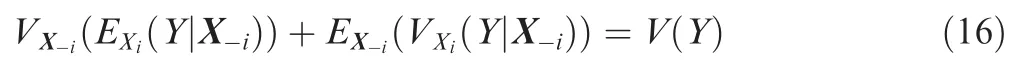
VX-i（EXi（Y|X-i）） can be seen as the first order effect of X-i,thusV（Y）minusVX-i（EXi（Y|X-i））should give the contribution of all terms in the variance decomposition which includesXi.To normalize the variance contribution, the main effect index is defined as

The variance based sensitivity index δican reflect the impact of geometrical changes of roller wheels due to wear on the robustness of the slat mechanism. Those significant roller wheels can be identified by such analysis, and extra attention can be paid to these wheels.

3.3. Failure probability based sensitivity index

According to the existent literature,16the failure probability based sensitivity index of the input variableXiis defined as

wherePfis the unconditional failure probability,PfYXiis the conditional failure probability withXibeing fixed at a realized value.The failure probability based sensitivity indexcharacterizes the average impact ofXion the failure probability of the mechanism as it varies within its range of distribution.

The exact expression of the failure probability is the integral of the joint probability density function of the input variables in the failure domain, which can be rewritten as the mathematical expectation of the failure domain indicator function,as is shown in Eq.(9)Similar to the unconditional failure probability, the conditional failure probability based on the realized value ofXican be expressed as

Based on Eqs. (18) and (19), we can get the relationship between failure probability based sensitivity index and variance-based sensitivity index of failure domain indicator function as17

As can be seen from the above equation,the failure probability based sensitivity index can be easily converted to the corresponding variance based sensitivity index of indicator function. Therefore, the calculation method of variance based sensitivity index can be used to compute the failure probability based sensitivity index.

3.4. Computational strategy based on artificial neural network

Since the focus of this work is to apply the reliability and global sensitivity to the slat mechanism, the straightforward Monte Carlo method is used to estimate the failure probability and sensitivity indices.However,as the computational time of directly calling ADAMS model of the slat mechanism is pretty long, surrogate model between the output response, i.e. the angle turned by the slat, and the geometrical abrasions, i.e.Δr2, Δr4, Δr6, Δr8, Δr10, Δr12, is established by use of artificial neural network in this section.

The theory of artificial neural networks is proposed in the research of modern neurobiology and human information processing by cognitive science, and they can obtain a variety of complex information processing functions by simulation of the neurons in the network structure and characteristics. Artificial neural network has the capability of establishing a functional relationship between two data spaces during the learning process and generalize these data during a recall process.That is to say,in one of their basic applications and after successful training, they can offer the correlating mathematical relationship between multi-dimensional input or output data sets as18:

whereqis the relationship function, X=［X1，X2，...，Xk］ and Y=［Y1，Y2，···，Yl］ are real input vector and real output vector,kis the input dimension, andlis the output dimension.Artificial neural networks are consisted of input layers,implicit layers and output layers, and each layer consists of some neurons,which is also called processing elements. A typical structure of artificial neural networks is shown as Fig. 2. More introduction of artificial neural networks can be seen in Ref.19,20,21A multi-layer feed-forward neural network structure, trained by back-propagation, is used in this study. And the specific architecture employed in this work is the same with that employed in Ref.22for the sake of accuracy and efficiency.

In this work, the surrogate model between θ and Δrm（m=2，4，6，8，10，12） is first established by use of artificial neural network. In this work, the number of samples used to train the artificial neural network is 1000. Then the failure probability and global sensitivity indices presented in previous sections are estimated by the Monte Carlo method.

4. Discussion of reliability and sensitivity results

According to Section 2,we can obtain the wear radius of roller wheels under different wear times,which is shown in Fig.3.As can be seen, the wear of the roller wheelr2andr6are significantly more obvious than the others, and the wear speed of the roller wheelr6is increasing dramatically. The result coincides well to the pressure that each roller wheel bears, which can be seen from Table 2.

The failure probability of the slat mechanism is different when it takes different failure threshold values. A smaller failure threshold value usually means a larger failure probability.As shown in Fig. 4, the failure probability of slat mechanism decreases as failure threshold value increases both at the takeoff stage and landing stage. When the same failure threshold value is taken, the probability of failure becomes larger as the wear times increases.This is consistent with the actual engineering experiences.

Since the service of civil airplane often spans a very long period, e.g. a quarter-century, the robustness of slat mechanism may suffer from the degradation of parts, such as the wear of roller wheels. Besides, the variation extent of wear abrasions also changes as the working environment of the slat mechanism is so complex. Thus, it is necessary to study the change of global sensitivity indices with the increase of wear times and abrasion variation. Furthermore, as the environment (e.g. aerodynamic load) of takeoff and landing stage is different, the sensitivity analysis should be separately considered.

Fig. 2 General structure of artificial neural network.

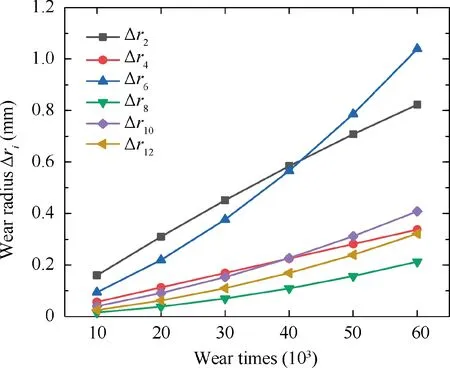
Fig. 3 Wear radius of roller wheels under different wear times.

As shown in Fig. 5, the left side shows the variance-based sensitivity result at the takeoff stage, and in the right side is the result at the landing stage. It can be seen that the global sensitivity index varies with the wear times,and the global sensitivity ranking may change in different wear times. When the wear times is less than 40000,based on the variance-based sensitivity index, the importance of the worn roller wheels can be ranked in the descending order as Δr2,Δr4,Δr6,Δr8,Δr10,Δr12.However,the ranking will become Δr6,Δr2,Δr4,Δr8,Δr12Δr10when the wear times reaches 60000.Overall,it is clear that the roller wheels designated asr2,r4,r6are more important than the rest.

Both different failure threshold values and different wear times have a significant impact on the failure probability.Therefore,the failure threshold value is fixed as 0.8 to calculate the failure probability based sensitivity index in different wear times and the result is shown in Fig.6.Note that we only show the sensitivity index results of roller wheels during 50000 to 51000 wear times. Then, the number of wear times is fixed at 50000 to calculate the failure probability based sensitivity index in different failure threshold values, and the result is shown in Fig. 7.

Fig.4 Failure probability varying with different failure threshold values at the takeoff stage as shown in left side,and that at the landing stage as shown in the right side.

Fig.5 Variance-based sensitivity index at the takeoff stage as shown in the left side,and that at the landing stage as shown in the right side.

As can be seen from Fig. 6, according to the results of the variance-based sensitivity index,the importance ranking of the worn roller wheels can be ranked in the descending order as Δr2, Δr6, Δr4, Δr8, Δr10, Δr12. And in Fig. 7, the failure probability based sensitivity index of all six roller wheels first increases and then decreases when the failure threshold value increases from 0 to 1.2.However,the global sensitivity ranking does not change substantially.

Now let us have a brief review of the reliability analysis results in Fig. 4 and the global sensitivity analysis results in Figs. 5-7. According to the results in Fig. 4, the failure probability of slat mechanism gradually decreases with the failure threshold value increases. Therefore, it is necessary to select a reasonable failure threshold value based on the demand for the output performance of the slat mechanism in the process of reliability analysis. According to Figs. 5-7, sensitivity indices of Δr2,Δr4and Δr6are obviously larger than the others.It means that the roller wheel designated asr2,r4andr6have the most obvious impact on the movement reliability and robustness of the slat mechanism. The analysis indicates that those roller wheels tied with higher sensitivity should be paid extra attention to as the service of the aircraft continues, and proper maintenance or even replacement is necessary at essential time. From the above analysis, it can be seen that the global sensitivity index does provide more underlying information for us.

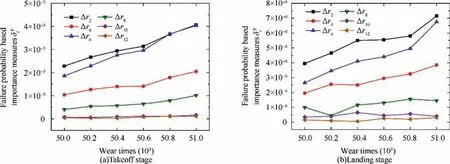
Fig.6 Failure probability based sensitivity index at the takeoff stage as shown in the left side,and that at the landing stage as shown in the right side.

Fig.7 Failure probability based sensitivity index varying with different failure threshold values at the takeoff stage as shown in the left side, and that at the landing stage as shown in the right side.

5. Conclusions

In this work, the reliability and sensitivity issue of the slat mechanism is studied. Due to the wide existence of uncertainties, the geometrical sizes of roller wheels after wear degradation also exhibit random uncertainties, which can affect the reliability and performance of the mechanism. Reliability model for the slat mechanism has been established,considering the accuracy requirement of the mechanism. Then sensitivity indices based on failure probability and variance are introduced,to study the effects of the worn roller wheels on the reliability and robustness of the mechanism. Results have shown that the mechanism reliability decreases as the wear times increases,and it is also relevant to the failure threshold values.The global sensitivity index results show that some roller wheels have obviously larger impacts on the mechanism reliability and robustness than the others,which means these roller wheels should be emphasized both in design and maintenance.This work proves that reliability and global sensitivity analysis can be of significant use in the aeronautical applications.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (NSFC51975476), the Natural Science Basic Research Plan in Shaanxi Province (2020JM-135) and Aerospace Science and Technology Foundation of China.