A review of topology optimization for additive manufacturing: Status and challenges

Jihong ZHU,Hn ZHOU,Chung WANG,Lu ZHOU,Shngqin YUAN,Weihong ZHANG

a State IJR Center of Aerospace Design and Additive Manufacturing, Northwestern Polytechnical University, Xi’an 710072, China

b MIIT Lab of Metal Additive Manufacturing and Innovative Design, Northwestern Polytechnical University, Xi’an 710072, China

c Institute of Intelligence Material and Structure, Unmanned System Technologies, Northwestern Polytechnical University, Xi’an 710072, China

KEYWORDS Additive manufacturing;Aerospace applications;Hierarchical structure;Manufacturing constraints;Material feature;Topology optimization

Abstract Topology optimization was developed as an advanced structural design methodology to generate innovative lightweight and high-performance configurations that are difficult to obtain with conventional ideas. Additive manufacturing is an advanced manufacturing technique building asdesigned structures via layer-by-layer joining material,providing an alternative pattern for complex components. The integration of topology optimization and additive manufacturing can make the most of their advantages and potentials,and has wide application prospects in modern manufacturing.This article reviews the main content and applications of the research on the integration of topology optimization and additive manufacturing in recent years, including multi-scale or hierarchical structural optimization design and topology optimization considering additive manufacturing constraints.Meanwhile,some challenges of structural design approaches for additive manufacturing are discussed,such as the performance characterization and scale effects of additively manufactured lattice structures, the anisotropy and fatigue performance of additively manufactured material, and additively manufactured functionally graded material issues, etc. It is shown that in the research of topology optimization for additive manufacturing,the integration of material,structure,process and performance is important to pursue high-performance,multi-functional and lightweight production.This article provides a reference for further related research and aerospace applications.

1. Introduction

Topology optimization1is an advanced structural design method which can obtain the optimal structure configuration via reasonable material distribution satisfying specified load conditions, performance and constraints. Compared to sizing and shape optimization,topology optimization is independent of the initial configuration and has a broader design space.Consequently, it has been developed as a mainstream structural design technique for high-performance, lightweight as well as multifunctional structures and been widely used in aerospace,2,3automotive,4architecture,5etc.A typical example of topology optimization solution is the leading edge droop nose ribs for Airbus 380, as shown in Fig. 1, which achieved structural weight saving design meeting all mechanical performance requirements.6Fig. 2 shows a typical topology optimization design of an aircraft pylon, which satisfied stiffness,strength and weight requirements.2Since Bendsøe and Kikuchi7proposed the seminal work, topology optimization has been developed rapidly. Apart from compliance-based structural topology optimization, periodic microstructure topology optimization for prescribed performance (e.g. negative Poisson’s ratio, extreme thermal expansion, etc.),8-14heat conduction structural topology optimization,15-18layout optimization of complex multi-component system,19-21concurrent optimization of microstructure and macrostructure22-31etc.have also attracted attentions of numerous researches.

Over last three decades, several topology optimization methods have been proposed, among which the densitybased method, the evolutionary structural optimization(ESO), the level set method (LSM) are the most representatives. In density-based method, a 0-1 discrete optimization problem is transformed into a continuous optimization problem in order to relax the binary design form. Originally, the homogenization method was utilized to map specified microstructure controlled by density variable to effective properties,but it is difficult to implement for mathematical complication.7Subsequently, Bendsøe and Kikuchi32proposed an alternative approach named solid isotropic material with penalization (SIMP). Compared to homogenization, element elastic modulus penalized exponentially in terms of density variables. SIMP has soon become the most popular topology optimization and been embedded in commercial software to solve engineering problems for its concise form.

The ESO method,first proposed by Xie and Steven,33gradually remove inefficient material via heuristic strategies until meeting prescribed material volume requirement,yet the effective solutions can be hardly obtained in some cases. To overcome this shortcoming, the bi-directional evolutionary structural optimization (BESO) method, an extension of ESO with allowing to add as well as remove material to modify structure,was proposed34-36and this method was proved to be reliable by Huang and Xie.37

Different from the above methods, LSM adopts highdimensional level set functions to describe structural boundary.38,39The optimum configuration with smooth structural boundary can be obtain via iteratively solving the Hamilton-Jacobi equation to update level set functions.Recently,Zhang et al.40,41proposed a feature-driven optimization method(FDO) derived from LSM, where complex engineering structure are explicitly decomposed into a set of simple geometric features (e.g. superellipse). Compared with density-based method,not only the number of design variables can be greatly reduced, but also zigzag boundary can be avoided in the optimum solutions. Guo et al.42,43proposed moving morphable components (MMC) and moving morphable voids (MMV).Literatures2,44,45summarized the progress and applications of topology optimization in detail.

Topologically optimized structures are generally characterized with complex geometric configuration. Therefore it is difficult to manufacture these innovate structures via conventional processes (e.g. machining, cast), thus additional treatments are often necessary to improve manufacturability which hardly realizes the full potential of topology optimization, as shown in Fig. 3.

Fig. 1 Topology, sizing and shape optimized A380 droop nose ribs.6

Fig. 2 Topology optimization design of aircraft pylon.2

2. Direct applications of topology optimization and additive manufacturing

Additive manufacturing (AM), also known as 3D printing,manufactures parts via joining material layer-by-layer. AM opens the possibility to manufacture complex structures especially for topology optimization structures.Without additional tools, molds and complicated procedures, AM is flexible for any complicated structures, which not only saves cost of production but shortens the manufacturing cycle especially in rapid prototyping and small batch production. In addition,AM’s potential for complex structures also promotes the design of integral structures that reduces the number of parts and assembly processes. Over last several decades of studies and applications, quite a lot of AM techniques have arisen including stereolithography (SLA),46selective laser sintering(SLS),47selective laser melting(SLM),48fused deposition modeling (FDM),49etc. AM materials cover metal, polymer, composite, biomaterial etc. AM parts ranges from micro-nano components to large structures of meters.Due to powerful personalized manufacturing capabilities, AM has broken the shackles of conventional manufacturing techniques and played a significant role in advanced manufacturing industry, which has broad application prospects in aerospace, mechatronics,medicine and civil engineering.3,50-53

For topology optimized structures,AM allows engineers to get rid of the limitations of conventional manufacturing techniques and pay main attention to design lightweight and highperformance structures. In turn, topology optimization is an effective approach for additively manufactured products with lightweight and innovative configuration. The integration of topology optimization and AM is an important way to achieve matching of structural design and manufacturing.

As shown in Fig. 4, topology optimization and AM were adopted to develop a cable mount on the front spar of the vertical stabilizer. Compared with the conventionally produced component consisting of more than 30 individual parts, this integrated solution merely consisting of a single part not only realized 30% weight reduction, but also significantly reduced construction and installation times. The antenna bracket for RUAG’s sentinel satellite (Fig. 5) is another representative example of successful application of topology optimization and AM. The optimized component’s minimum rigidity requirements exceeded by more than 30%and weight reduced to 940 g from 1.6 kg. Moreover, many competitions such as‘‘Backbone cup” sponsored by Northwestern Polytechnical University (NWPU), ‘‘Tiangong cup” sponsored by China Aerospace Science and Industry Corporation Limited(CASIC) and 3D printed structural optimization design competition sponsored by Commercial Aircraft Corporation of China Ltd(COMAC),were held in order to inspire researchers and engineers to design innovative structures and promote application of topology optimization and AM.

Fig. 3 A topology optimization design cannot be fabricated as an integrity in NC machining, which have to be segmented then assembled (https://whuborhub.wordpress.com/2014/10/16/thesis-summary/).

Fig. 4 A cable mount on the front spar of the vertical stabilizer for Airbus A350 XWB (https://www.eos.info/en/3d-printingexamples-applications/innovation-stories/airbus-a350-xwb-3d-printedcable-mount).

Fig. 5 Antenna bracket for RUAG’s sentinel satellite (https://www.eos.info/en/3d-printing-examples-applications/innovation-stories/ruag-aerospace-3d-printed-satellite-components).

Fig.6 shows a typical optimization design and AM process for an aerospace bracket developed by NWPU and CASIC.Three key steps, i.e. topology optimization as well as reconstruction, sizing optimization and fabricated part via SLM are involved in this procedure. Generally, topology optimization is used for structural conceptual design while sizing and shape optimization are used for structural detailed design.

Besides enormous manufacturing potential, AM leads to new structural design constraints and manufacturing defects,such as accuracy, structural connectivity, additional support structure, surface roughness, material properties, etc. Design for additive manufacturing (DAM)54-57requires to deeply integrate product design and manufacturing via considering AM process constraints and real material properties during AM, and takes full advantage of AM to maximize product performance.

In mainstream structural design and manufacturing pattern, topology optimization is generally regarded as a conceptual design method. Manufacturing constraints, detailed engineering features and subsequent sizing and shape optimization are considered and added in the reconstructed structure that may be inconsistent with the topologically optimized configuration. Consequently, this sequential design procedure cannot completely exploit the potential of topology optimization and AM versus more advanced design approaches need be explored to pursue efficient and innovative structures.

Fig. 6 Aerospace bracket designed by topology optimization and manufactured by AM.3

3. Hotspots in topology optimization for AM

The reconstruction of topology optimized schemes, direct additive manufacturing for applications are the main means to achieve rapid optimization design and manufacturing in the industry. In order to further take full advantages of both topology optimization and AM,the current research on topology optimization for AM mainly concentrates on two aspects:one is to design high-performance as well as additive manufacturing multi-scale/multi-hierarchical structure,and the other is to integrate AM design constraints into topology optimization to achieve product design and manufacturing integration.

3.1. Optimization design of multi-scale/multi-hierarchical structure

As a class of lightweight and multifunctional (specific strength,58heat,59energy dissipation,60vibration,61etc.)structures, lattice structures as well as porous microstructures have attracted more and more attention from researchers62-67.Fig.7 shows several lattice structures with different configurations. Not only complicated procedures but long working hours are required to manufacture lattice structures via conventional techniques (machining, welding, weaving, etc.).62As a type of self-supporting structures, complex lattice structures as well as hierarchical structures can be additive manufactured such as SLM quickly and accurately.63,64Fig. 8 exhibits a satellite bracket filled with lattice developed by Northwestern Polytechnical University, of which the dynamic response is reduced by 25%and the weight is reduced by 17%compared with the original design.

3.1.1. Hierarchical lattice structural optimization

In recent years, the optimization design of multi-scale or hierarchical lattice structures has been a key research field in the integration of topology optimization and AM and attracted widespread attention from researchers,which include:(1)hierarchical structural design derived from mapping combined with density-based method, (2) hierarchical structural design based on large scale strut-sizing optimization, (3) concurrent optimization of macrostructure and microstructure based on homogenization.

The mapping combined with density-based method is a degenerate SIMP method, and the density distribution tends towards continuousness and gradient when canceling exponential penalization. Although the computational procedure is easy to implement,the lattice configuration is generally simple to some extent. Zhang et al.68proposed a variable-density hexagonal cellular structural optimization design method.More specifically, homogenization method was first implemented to obtain the equivalent material constitutive law to represent cellular structures.Thereafter,topology optimization was conducted to obtain the optimum density distribution,which was mapped into explicit cellular structure in the later construction stage. Fig. 9(a) shows optimal density distribution and mapped lattice structure of a half simply supported beam. In the researches of Jing et al.,69an irregular cellular structural modeling technique based on tangent circles was proposed, which automatically generate the main outline of irregular cellular structure.

Likewise, all cellular structures could be determined according to topology optimized solution.Panesar et al.65conducted SIMP topology optimization to obtain multiple lattice structures, including uniform lattice structure, graded lattice structure (also called solid-lattice hybrid structure) and scaled lattice structure. The finite element analysis results show that the mechanical performance of lattice solution is worse than solid solution, but graded lattice solution and scaled lattice solution can improve significant mechanical performance compared with uniform lattice structure. Although the density mapping-based method is easy to implement, it is hard to obtain hierarchical structure with multiple lattice configurations.

Fig. 7 Typical lattice samples.

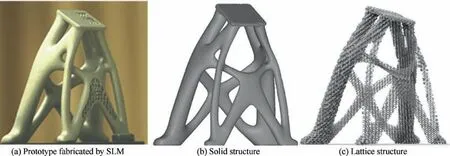
Fig. 8 A satellite bracket filled with lattice.

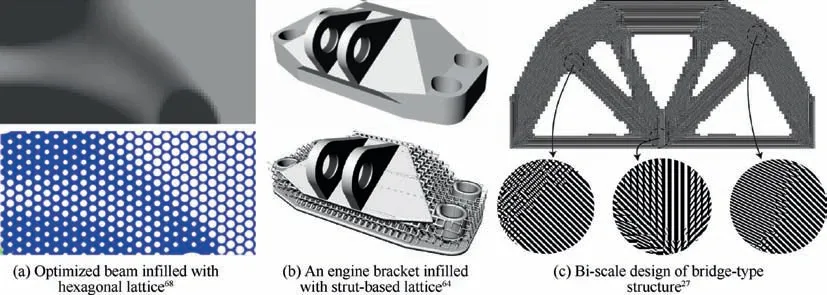
Fig. 9 Some topology optimization examples for hierarchical structures.

For truss-based lattice structure,lattice unit cell only serves as an auxiliary modeling tool, while each strut is utilized as basic unit in numerical analysis procedure. Strut-sizing optimization is implemented to obtain graded hierarchical structures. As presented in literature,70,71a so-called size matching and scaling (SMS) method focusing on the sizing optimization of struts was utilized to design mesoscale lattice structure. In this method, lattice structural topology was generated via a set of pre-defined lattice configuration and struts’size was directly determined by stress distribution of solidbody finite element analysis. It is worth noting that this method could directly generate a lattice structure based on a heuristic strategy with higher computing efficiency and less computing costing, but could hardly get the optimum configuration.

Chen et al.72combined meshing technique and pre-defined lattice cell units based on element type, element nodes and their connect relationships to model a large-scale parametric lattice structure.Moving iso-surface threshold method and sizing optimization algorithm were implemented to modify struts’cross-sectional areas to obtain optimum graded lattice structure. Since pure lattice structures without functional solids and surfaces are difficult to assemble for practical structures,Tang et al.64proposed a lattice-skin structural optimization design method, in which only functional volumes with lattice were optimized. Meanwhile, functional volumes with solids as well as functional surfaces were preserved, as shown in Fig. 9(b).

Another representative approach for hierarchical structures is multi-scale concurrent topology optimization of material and structure, in which the homogenization method plays a significant role in bridging microstructures and material properties, thus both microstructure and macrostructure can be optimized to obtain higher-performance scheme. Rodrigues et al.30proposed a hierarchical algorithm to optimize material distribution and local microstructures.And this algorithm was extended to 3D structural optimization by Coelho et al.29hereafter. However, two independent computational procedures were executed to determine macrostructure and microstructure respectively, which cannot realize concurrent multiscale structural optimization. Liu et al.28and Chen et al.23proposed a concurrent topology optimization strategy for macrostructure and microstructure. Uniform microstructure hypothesis was formulated to guarantee manufacturability as well as low computational cost. Moreover, literatures73-76reported the above hypothesis was utilized for thermomechanical design and dynamic response design.

To pursue higher-performance structures, concurrent topology optimization of material and structure based on FE2nonlinear multiscale analysis work was proposed by Xia and Breitkopf.24,27As shown in Fig.9(c),cellular material varied from point to point at the macro scale to adapt the macroscopic structural physical response, which not only lead to intensive computational cost but weaken manufacturability.To balance computational cost and design freedom, Wang et al.22,25proposed a hierarchical structural optimization method with parameterized lattice microstructure, in which two types of design variables were introduced into densitybased topology optimization to determine both macrostructure and pointwise lattice microstructure concurrently. More specifically, parameterized interpolation for lattice material(PILM), i.e. a series of polynomial functions bridging lattice control variables and effective mechanical properties, were constructed before optimization to save computational cost.An optimized three-point bending beam and additive manufactured samples were shown in Fig.10.Both numerical simulation and mechanical experiment demonstrated that nonuniform lattice structure is better than uniform lattice structure. In this method, parametrized lattice ensured both the connectivity of adjacent microstructures and manufacturability.

3.1.2. Hierarchical stiffened thin-wall structural optimization

Hierarchical stiffened thin-wall consisting of major stiffeners and minor stiffeners is a kind of widely used lightweight structural configuration in aerospace structures,e.g.launch vehicles and aircraft wings,77as shown in Fig. 11 and Fig. 12. Since increased global dimensions and multiple local features, bulking analysis and structural optimization generally suffer from heavy computational costs. The minor stiffeners are smeared to improve computing efficiency and the major stiffeners are retained to accurately predict the dominated partial overall bulking mode and overall bulking mode.78,79Thus, Smeared Stiffener Method (SSM) and asymptotic homogenization method were adopted to convert minor stiffeners and corresponding skin into an equivalent unstiffened skin.Hao et al.79and Wang et al.78,80proposed a hybrid optimization framework of hierarchical stiffened shell to explore loading efficiency. Notably, imperfection sensitivity should be taken into consideration during optimization due to the bulking load deviations between imperfect shell structures and perfect shell structures.81Hao et al.82also developed a hybrid optimization of cylindrical stiffened shells with reinforced cutouts by curvilinear stiffeners. More specifically, the near field around the cutout which would be filled with curvilinear stiffeners was first determined as design domain via an adaptive method and a bilevel optimization strategy was adopted to design the curvilinear stiffener layout, number, section profile and location.

3.2. Topology optimization considering AM constraints

Typical AM constraints includes minimum length constraints,connectivity constraints and overhang constraints.83As shown in Fig.13,the downward face becomes rougher and eventually the part will fail with overhang angle decreasing. The critical overhang angle and strut diameter of Ti-6Al-4V part fabricated by SLM were measured via experiment in.84How to integrate these AM constraints into topology optimization is a hot issue in recent research.

3.2.1. Length scale constraints

Limited by the manufacturing accuracy of 3D printing equipment,topology optimized structure could hardly be additively manufactured directly. Consequently, imposing length scale constraints in topology optimization is crucial to avoid unmanufacturable geometric feature such as small holes,thin-walls, tiny-hinges, etc. For density-based topology optimization,density filtering is an effective approach to constraint minimum length scale.85-87For instance, Heaviside step filter introduced by Guest et al.85and modified Heaviside filter introduced by Sigmund86ensure minimum length scale on the solid phase and void phase, respectively. Wang et al.87put forward a general filtering formulation called threshold projection,which can constraint minimum length scale of both solid and void. Zhou et al.88proposed density gradient approach to impose minimum length scale by identifying solid and void phase. Yang et al.89analyzed and compared three gradient operators including the orthogonal central difference scheme, Prewitt operator and Sobel operator. It is found the Prewitt operation considering boundary modification could calculate density gradient more accurately.

Moreover, minimum length scale was also found imposing in LSM-based topology optimization.90-93For example, in MMC topology optimization framework, minimum length scale of each component can be controlled by dimensional variables. Special treatments are required to control the minimum length scale on the intersection regions of components.92,93Liu90proposed a piecewise length scale control method for LSM-based topology optimization. The topology design can be decomposed into several strip-like components and each component’s length scale can be dynamically constrained according to real-time status.Xia and Shi91characterized structural length scale as the size maximal inscribable ball and introduced structural skeleton obtained via fast marching method to eliminate invalid tiny geometric features. Based on the above concepts,length scale control could be explicitly formulated as distance constraints from boundary to skeleton.Length scale control technique in topology optimization has been relatively mature and been integrated into the commercial software such as Altair OptiStruct. As shown in Fig. 14,unmanufacturable branches disappears when imposing the minimum length scale.

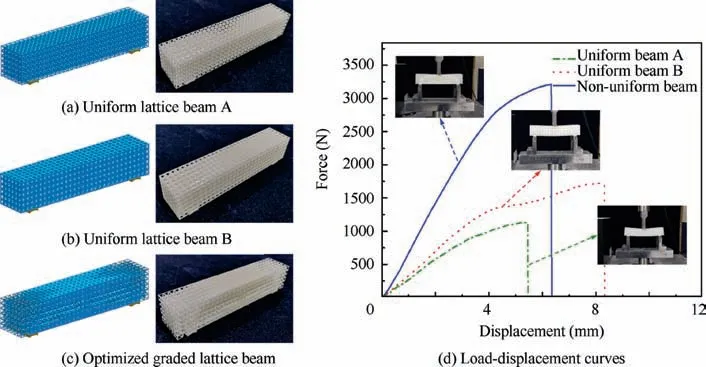
Fig. 10 Three-point bending beam infilled with uniform and graded lattice.22

Fig. 11 NASA Space Launch System rocket and stiffened shell.80

Fig. 12 Lattice infilled shell designed and fabricated by Shanghai Institute of Astronautical System Engineering, Northwestern Polytechnical University and Bright Laser Technologies Co.

3.2.2. Connectivity constraints

During AM process,it’s impossible to remove unmelt powders and supports in enclosed voids. Thus, eliminating enclosed voids is quite crucial to ensure structural manufacturability.Liu et al.94and Li et al.95proposed a so-called virtual temperature method to convert connectivity constraints to an equivalent maximum temperature constraints. The void region is filled with high heat conductive material and continuously heated, while the solid is filled thermal insulation material.Since enclosed voids lead to local high temperature,constraining the maximum temperature can force to eliminate enclosed voids. But extra finite element analysis procedure increases computational cost. Zhou and Zhang96proposed an effective approach to eliminating enclosed voids in feature-driven topology optimization by bonding design variables related to center points of void features outside the design domain. Another representative approach to avoiding enclosed voids is selectively creating tunnels that connect voids with structural boundary during topology optimization process.97This approach can generate a material distribution which is similar to free topology optimization, as shown in Fig. 15.

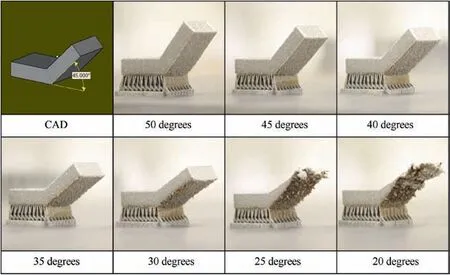
Fig. 13 Manufacturability of cantilever structures with decreased overhang angles (https://www.additivemanufacturing.media/blog/post/7-helpful-numbers-quantify-design-rules-for-am).

Fig. 14 Topology optimization of C-clip in Altair OptiStruct.

3.2.3. Self-support structural design

In AM process,additional supports are required to avoid overhang structures collapsing, as shown in Fig. 16(a). Supports should be removed generally through machining after manufacturing, as shown in Fig. 16(b). Additional supports reduce material efficiency and their removal increases postprocessing time and difficulties.

Many investigations have been made to slim down additional supports during additive manufacturing process. Morgan et al.99pursued the optimum building orientation to minimum the volume of additive supports via single objective optimization technique. To further reduce the additional supports, Hu et al.100proposed an orientation-driven shape optimization approach to achieve self-supporting structure.Global rigidity energy is formulated as objective to minimize the shape variation. But this approach is only applicable for the case where the initial design is allowed to be adjusted.

Fig. 15 Topology optimization of a platform.97

Fig. 16 Additively manufactured upright.98

Designing innovative and efficient support structure instead of conventional supports is another case for slimming down supports. Mezzadri et al.101formulated the generation of supports as a topology optimization problem with length scale control and manufacturability constraints.The optimized supports as shown in Fig. 17(a) employ less material than those generated in existing software. Zhou et al.102proposed a tree-like support generation approach based on the L-system and octree as shown in Fig. 17(b). These supports are easier to remove and require less material as well as building time.

Integrating overhang constraints into topology optimization to pursue self-supported structure is one of current research hotspots. Fig. 18 exhibits a comparison of non-selfsupporting design and self-supporting design.Similar to length scale constraints,overhang constraints can also be imposed via density projection in density-based topology optimization.103Only those should be projected to solid and satisfy overhang constraints are preserved via a combination of a local projection. This merely requires a series of projection operations without additional explicit geometric constraints.This method was extended to design 3D self-supported structures by Johnson and Gaynor.104Additionally,an improved overhang mapping procedure was adopted to exactly impose allowable overhang angle via adjusting the spacing of the design points.And adjoint approach to sensitivity analysis was adopted to speed up the calculation procedure, which could be easily applied to large scale structural optimization problem. Similarly, an AM filtering procedure was proposed in Langelaar’s work,105,106which acted as a simplified layer-wise printing simulation to exclude unprintable parts from the optimum resolution. And this layer-wise filtering concept was also further applied and studied in literatures.107-110

Based on Heaviside projection-based aggregations,Qian111and Wang112explored an effective overhang angle constraint approach, which transformed pointwise overhang angle constraints into two integral inequalities, i.e. directional gradient based global constraint to eliminate internal supports and gradient-based global constraint to avoid external supports. Moreover, Mass and Amir113proposed an alternative two-step approach using a virtual skeleton. Overhang constraints are converted into a combinatorial optimization problem. Truss optimization is firstly implemented to obtain a discrete skeleton that satisfies overhang constraints. Then the optimum discrete pattern is mapped to a continuum structure and density-based topology optimization is implemented to relax stress concentration around intersection of bars.

For LSM-based topology optimization, overhang constraints could also be directly imposed via explicit geometric constraints. Allaire et al.114adopted anisotropic perimeter functions to penalize overhang features.While these geometric constraints could not avoid unprintable V-shape regions within critical overhang angle. To overcome the limitation,an alternative mechanical overhang constraint formulation based on simplified layer-wise printing process was proposed.114,115The self-weight manufacturing compliance of intermediate shape during the layer-by-layer assembly was selected to estimate whether the final shape could be manufactured smoothly. However, these mechanical constraints could not eliminate completely plat overhang features due to that each layer was assumed to be deposited instantaneously. A combination of geometric constraints and mechanical constraints was developed to pursue self-support structures effectively.114Guo et al.116proposed two effective approaches based on MMC and MMV frameworks respectively.The treatment of geometric constraints includes two parts, i.e. the constraint on each void feature to obtain a printable shape, and the constraint on any different voids from intersecting during optimization procedure.Zhang and Zhou117proposed an analogous approach based on polygon void features, which are easier to impose geometric angle constraints. The difference is that polygon fusion algorithm is formulated to eliminate unprintable V-shape region caused by intersecting polygons.

3.3. Remarks

A summary collection of research about topology optimization for AM is shown in Table 1. Note that there are still lots of related study not included in this section due to limited space.Topology optimization for AM reveals abroad engineering application prospects of pursuing high-performance and lightweight structures. It is highly convinced that more and more industrial structures will be designed and fabricated with the help of the integration of topology optimization and AM in the future. However, practical industrial structures are generally characterized with irregular shape and large geometric dimensions, which leads to their numerical simulation and optimization cost-prohibitive in term of time and computing burden. Fortunately, the development of massively parallel computing versus high-performance simulation118,119makes it applicable for large-scale engineering structures. Moreover,most researches were subjected to ideal material model, e.g.isotropic material, which hardly exists in practical structures,especially additively manufactured structures. In this regard,some challenges for further integration and application of topology optimization and AM are presented in the following section.

4. Challenges for future integration and application

In recent years,AM integrated with topology optimization has become a hotspot in the field of mechanical design and manufacturing. Numerous achievements have been made in engineering applications and academic research. However, due to the feature of additively manufactured structures and their optimization design, more challenges are encountered. On the one hand,facing the requirements of multiscale and multifunctional structures, topology optimization and its numerical design schemes have many contents to be developed. On the other hand, AM itself shall be improved by predicting and controlling its material mechanics behaviors, fabricating more complicated functional structures etc.to realize the integration of material, structure, process and performance.

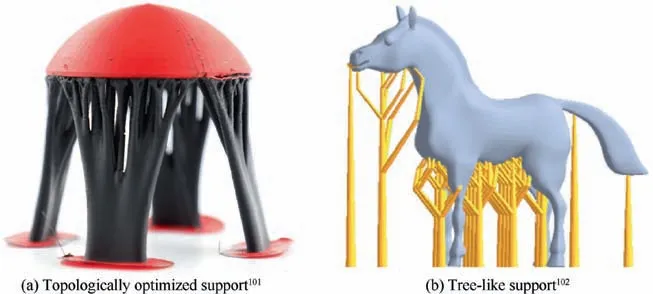
Fig. 17 Innovative support structures.

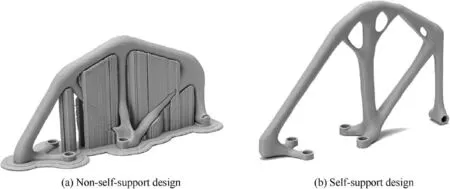
Fig. 18 3D printed topologically optimized industrial frame.109

4.1. Effective properties prediction of lattice structure

In large-scale hierarchical structural analysis and topology optimization for additive manufacturing,homogenization theory plays a significant role in bridging microscale and macroscale.Homogenization120relies on an asymptotic expansion of the governing equations to realize structural analysis at separate scales.With the help of homogenization,not only material effective properties but also physical field (e.g. stress) on the microscopic scale can be simulated. Thus homogenization is widely used in multi-scale structural analysis of composite material121,122and structural design of periodic microstructures.9,14

To overcome the difficulties of numerical calculation and sensitivity derivation,an equivalent energy-based homogenization was also proposed to predict the effective properties of microstructure.13The stress and strain tensors of the equivalent homogenous medium are equal to the average stress and strain tensors of the periodic microstructures. The strain energy density in microstructure is equal to that in the equivalent homogenous medium. Only four simple load cases are required to calculate stiffness tensor for 2D orthotropic microstructure and nine are required for 3D cases. Moreover,the energy-based approaches to predict effective coefficient of thermal expansion and thermal conductivities are also proposed in literatures.123,124

Homogenization is based on periodic hypothesis and scale separation hypothesis,8while additive manufactured lattice and hierarchical structures are always non-periodic and scale-dependent. Thus, how to characterize the microstructures’ equivalent performance is an essential challenge. As shown is Fig. 19, Dirichlet bulk modulus and Neumann bulk modulus converge on the homogenized bulk modulus of periodic composite only when the scale factor converges to infinity.125Many efforts have been done trying to solve this challenge. Yan et al.126used the extended multiscale finite element method to study the scale effect of lattice microstructure and minimize the weight of scale-related lattice structure.Wu et al.127developed an approximation of reduced substructure with penalization model to optimize scale-related hierarchical structure, which regards each lattice unit cell as a substructure.

The beam element approach, which employs 3D beam elements for modeling the lattice structure,72,128,129is an alternative approach without scale effect. Dong et al.128proposed a hybrid elements model to simulate elastic properties of solidlattice hybrid structures.In his method,Timoshenko beam elements and 3D solid elements are applied to mesh lattice part and solid part respectively. Rigid Body Elements (RBEs) are applied to create connection between beam elements and solid elements. Fig. 20 shows a topologically optimized solid-lattice structure. Although beam element model can save computational cost and avoid poor elements, it suffers from two deviations, i.e., overestimation of material volume at overlapping domains and underestimation of both stiffness and strength in the vicinity of the vertices.130

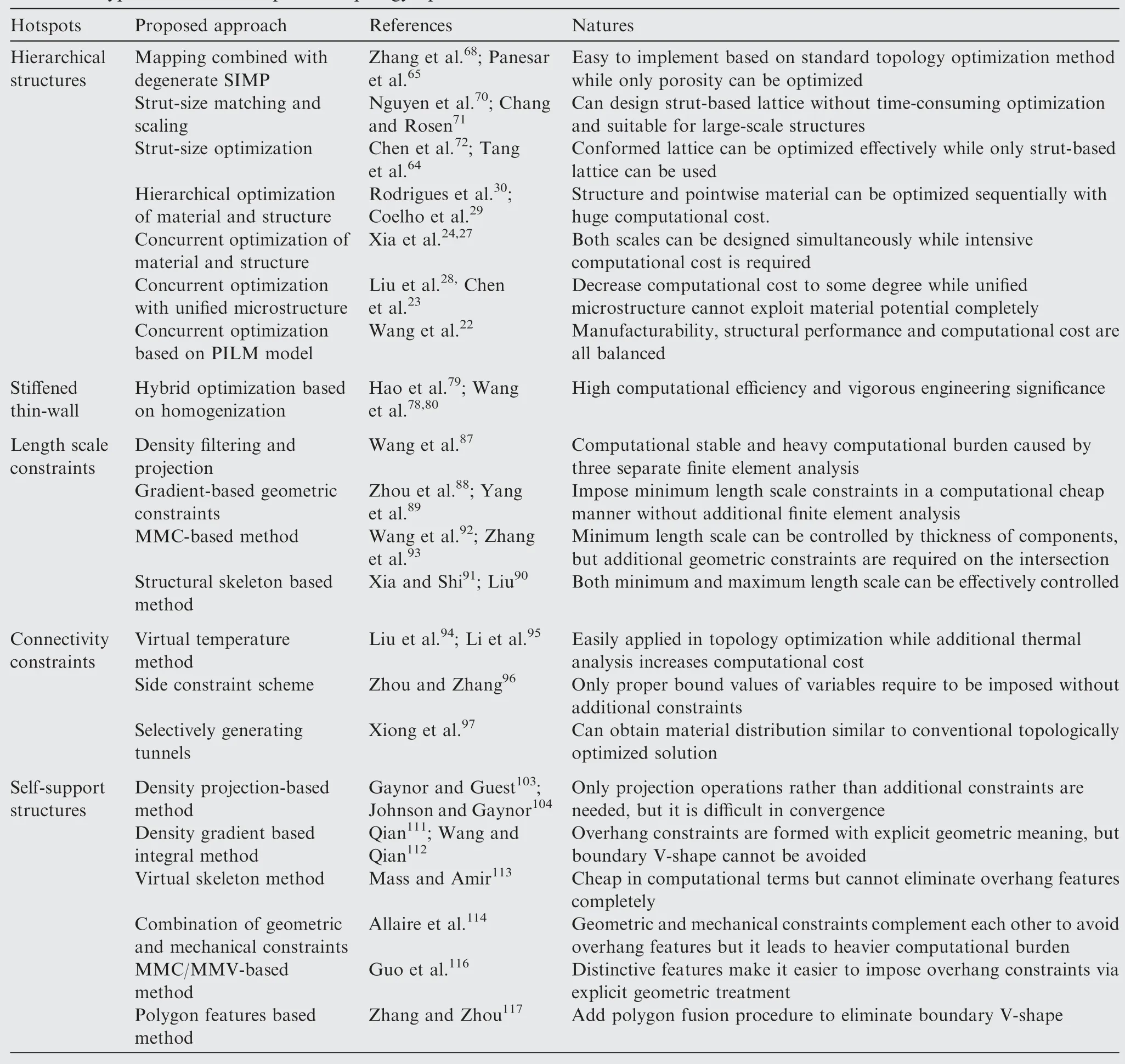
Table 1 Typical research hotspots in topology optimization for AM.

According to Luxner et al.,130material distribution around vertices could be approximated by a sphere whose radius equal to strut radius and material stiffness within the spherical domain was magnified by 1000 times to compensate these deviations. Labeas and Sunaric131and Smith et al.132adopted another compensation approach to approximating the deviations derived from material aggregation, i.e., reasonably increasing the cross-section at the end of each strut. Although abovementioned approximations can compensate deviations to some extent, they are generally empirical and their analysis accuracy closely depends on the complexity of the vertices.

Meng et al.133proposed a systematic inverse approach to accurately modelling additively manufactured lattice core based on variable cross-section beam elements. To be specific,each idealized uniform beam was substituted by three beams consisting two enhanced tapered beams close to intersecting nodes and one uniform beam in-between. The proposed variable cross-section beam could be characterized by four geometric parameters. These parameters can be obtained via solving a minimum approximation problem. Notably, since the four geometric parameters can be identified by real experiment data, this approach can also take geometric accuracy and structural defects derived from AM process into consideration.

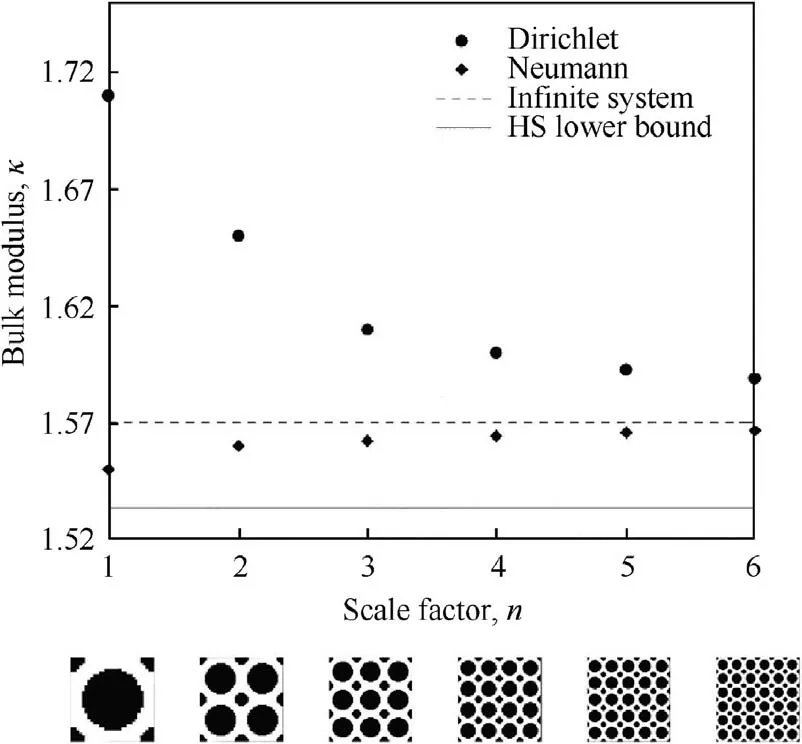
Fig.19 Equivalent Dirichlet and Neumann bulk modulus of the stiff composite with increasing scale factor.125

Fig. 20 A topologically optimized solid-lattice hybrid structure(http://fea.ru/news/6697).

4.2. Material anisotropy in additive manufacturing

The mechanical properties anisotropy in AM material is an essential challenge for structural design and application.Plenty of experimental observations demonstrate that the as-built material microstructures are diverse in horizontal plane perpendicular to the building direction and vertical plane parallel to the building direction.134-137The anisotropy of mechanical properties is mainly caused by the anisotropy of microstructure. As shown in Fig. 21(a), the material microstructures of the cold sprayed copper deposits exhibit an equiaxed shape in horizontal plane, while a lens-like shape is exhibited in vertical plane. As a result, the microhardness in horizontal plane is lower than in vertical plane.135According to in Fig. 21(b),during Ti-6Al-4 V additive manufacturing process, the priorβ grains grow in a columnar way almost parallel to building direction,which affects the fracture mechanisms and the crack propagation in the parts.136Similarly, the microstructure of 17-4 PH stainless steel specimen manufactured via SLM is characterized by complex directional or columnar lath martensite parallel to the building direction,137as shown in Fig.21(c).

Besides metal material, additively manufactured polymer material also exhibits the anisotropy of both microstructure and mechanical properties.Yang et al.67found that SLA manufactured material is almost transversely isotropic in elastic behavior and its mechanical properties, including elastic modulus,yield strength and fracture strain,in horizontal plane are better than that along building direction, as shown in Fig. 22.

However,the idealized isotropic material models have been mainly applied in topology optimization, ignoring the effects of material anisotropy on structural design as well as performance. To overcome this challenge, we can (1) optimize additive manufacturing process parameters, such as building direction136,138and nozzle scanning strategy135together with the structural configurations,(2)improve additive manufacturing process, e.g. employ secondary processes consisting of selective laser erosion and laser re-melting,139(3) introduce the real anisotropic material model into topology optimization67to pursue higher-performance additively manufactured structures.

4.3. Structural fatigue performance in additive manufacturing

Both long-life aircrafts and reusable space vehicles require structures with high fatigue performance. But the fatigue life and fatigue strength of additively manufactured material are significantly lower than those of corresponding wrought material,140for instance,the fatigue performance of SLM manufactured 17-4 PH stainless steel is weaker than its wrought form according to Fig. 23(a),140which not only limits additively manufactured material’s application in aerospace field but also brings new challenges for further research on topology optimization for additive manufacturing.

Defects produced in additive manufacturing process including un-melt regions due to lack of fusion as shown in Fig.23(b)and pores due to entrapped gas as shown in Fig. 23(c) are the main cause of fatigue failure.138These defects typically serve as crack initiation sites under cyclic loading. The location, size and shape of void defects significantly affects the fatigue performance of additively manufactured material.The high stress concentrations mainly occur around void defects of large size and irregular shape closing to surface, which are detrimental to fatigue performance. Researches138,140show that the location of void defects is the leading contributor for fatigue failure in most cases.

The main factors that affect additively manufactured parts’fatigue performance also includes geometry,building direction and surface roughness. The part geometry as well as the number of parts manufactured per build operation directly affects inter-layer time interval,which is closely related to thermal history experienced during manufacturing. The distinct thermal history leads to various microstructural features including grain structure and defect distribution. In the study of direct laser deposited 316L stainless steel,141longer inter-layer time interval and larger cooling rates along each layer lead to finer grain structure, higher yield and tensile strength as well as lower elongation to failure.But longer cooling time diminishes the initial layer temperature and laser melting pool, which is easier to produce un-melted regions and weaken fatigue performance.The microstructural anisotropy of additively manufactured material, including grain and defect directionalities,also leads to anisotropic fatigue performance. For instance,selective laser melted 17-4 PH stainless steel138and Ti-6Al-4V142exhibit better fatigue performance perpendicular to the building direction than parallel.To improve the fatigue performance of as-built parts, hot isostatic pressing (HIP),142the most effective post-manufacturing treatments to remedy defects produced in additive manufacturing process is applied.Via a combined action of high temperature and high pressure,HIP can eliminate part of void defects and homogenize the microstructure, which significantly improve fatigue performance. In addition, surface treatment (e.g. machining, polishing) can also improve the fatigue performance of additively manufactured parts.143However,affected by the defects distribution and cutting thickness, machining may resurface the inner defects occasionally, which leads to poorer fatigue performance instead.140

Due to geometric difference,experimental samples and real parts experience different thermal history and produce different microstructures and defect distribution. Thus, the fatigue performance of real parts cannot be accurately characterized by that of experimental samples. Moreover, the postmanufacturing treatments to improve fatigue performance also depends on material properties.For instance,HIP is less effective to improve fatigue performance of 316L stainless steel due to its high ductility.144

Fig. 21 Some additively manufactured material microstructures.

Fig. 22 Load-displacement curves of tensile samples with different building directions fabricated by SLA in tensile experiments.67

Moreover, efficient structural configuration can notably r educe stress level subject to dynamic loads to ameliorate fatigue performance. Generally, fatigue-related topology optimization can be formulated as two optimization problems,i.e. fatigue performance such as fatigue life is considered as optimization objective functions and constraints respectively.Since the difficulty of sensitivity analysis and high nonlinearity of damage with regard to design variables,taking fatigue performance into topology optimization is still a crucial challenge. Holmberg et al.145proposed an efficient fatigueconstrained structural optimization procedure including two separate steps,i.e. fatigue analysis and topology optimization.Fatigue analysis was first performed to obtain critical fatigue stress, which was subsequently set as an upper bound of fatigue stress level during topology optimization.To pursue structures with prescribed high-cycle fatigue life, Oest and Lund146directly treated fatigue damage accumulation subject to proportional loads as constraints. Palmgren-Miner’s linear damage hypothesis, S-N curves and Sines fatigue criterion were utilized to save computational costs during optimization. For non-proportional loads, Zhang et al.147formulated loading history as a linear combination of a set of simple unit loads,which could efficiently compute pointwise stresses and sensitivities via linear superposition. Zhao et al.148constructed dynamic-fatigue-constrained topology optimization model with dynamic random loads, where fatigue constraints could be expressed as the peak value of the period fluctuating dynamic stress. And a constraint-limit-variant method was proposed to solve this highly nonlinear optimization problem.

Consequently, establishing an effective model relating material, structure, process and fatigue performance remains a challenging topic and is crucial for pursuing reliable engineering structures with high fatigue performance.

4.4. Design and manufacturing of functionally graded material

Functionally graded material (FGM) is an advanced composite material composed of two or more materials,whose compositions or properties vary gradually along one or more directions to adapt to extreme loading circumstance. FGM has wide engineering application prospects and is also a new direction for the integration of multi-phase material additive manufacturing and topology optimization.

Fig. 24(a) shows a typical FGM form with grain size gradually changing. Compared to conventional composite material, FGM can effectively relax or even avoid interfacial stress due to steep shifts in material properties via changing each material phase distribution gradually. As shown in Fig. 24(b), a C/SiC FGM designed by Kim et al. effectively relaxed the residual thermal stress between the carbon fiberreinforced carbon composites and the SiC coating layer, and increased the oxidation resistance.149-152

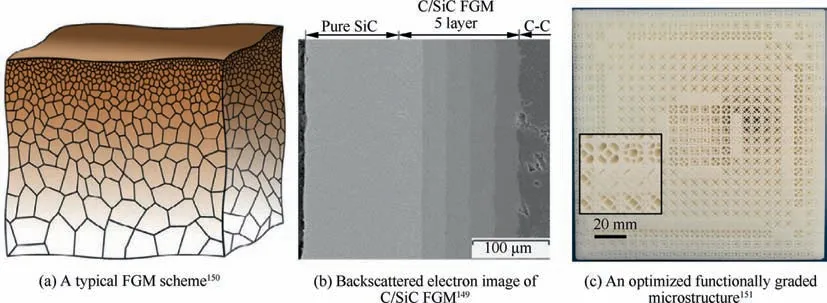
Fig. 24 Illustrations of FGMs.

At present, the design of FGM mainly focuses on twophase materials.Material composition usually changes according to preset direction and mode, which hardly fully realizes FGM’s potential. Literature152gives a detailed review of FGM’s design method for basic engineering structures (e.g.beam,plate,shell).The development of topology optimization further enriches FGM’s design method. Liu et al.151utilized topology optimization to conceive tailored FGM with specific stiffness-related and failure-related mechanical properties.SLA is adopted to manufacture these optimized functionally graded structures as shown in Fig.24(c).Concurrent optimization of material properties and structural topology is an effective approach for high-performance FGM. Xia and Wang153integrated two design variables, i.e. the material distribution and the structural boundary, into a compliance optimization.Lieu and Lee154proposed a multi-material topology optimization approach in the framework of isogeometric analysis,which utilizes bivariate B-spline basic functions to describe material distribution. Apart from single stiffness-related design, Banh and Lee155proposed a multi-material topology optimization design dependent on crack patterns, which concurrently optimizes both material distribution and structure to prevent the propagation of crack.

Multi-material AM is the most ideal manufacturing method for FGM,156,157but there still exists plenty of problems to be further investigated, including multi-material fusion mechanism, material properties and manufacturing process limitations. Mixed metal powders repeatedly experience complex thermal history including melting, molten pool flowing and crystallizing under the action of laser. And structural defects such as pores, un-melted regions and cracks are sensitive to AM process parameters, which significantly affects FGM’s performance. Due to diversity thermodynamic properties of multi-materials, constant laser power easily causes material with high melting points or low laser absorption rates to fail to melt sufficiently. Consequently, it is necessary to dynamically adjust the laser parameters to adapt to the gradient changes of the material distribution.158In addition, thermal histories (e.g. cooling rate) usually severely affects microstructural feature such as grain morphology and defects, which in turn affects FGM’s performance such as strength and hardness.The thermal history is not only related to process parameters(e.g.laser power,scanning speed,scanning path),but also closely related to geometric model and deposition height.159For complex multi-material AM systems, how to accurately control thermal history is still a complicated and challenging research topic.

Simultaneously design and 3D printing integral components consisting of functional electronic device and substrate structure are challenging applications of multi-material functional structural design and AM. Sun et al.160fabricated 3D interdigitated Li-ion micro-battery on a sub-millimeter scale via accurately depositing cathode and anode inks with the assistance of fine deposition nozzles, as shown in Fig. 25.The printed micro-battery was characterized by high-aspect ratio electrodes in interdigitated architectures and exhibited higher areal energy and power densities than its rechargeable counterparts.Du et al.161utilized a 3D solution printer to first fabricate n-type flexible tungsten carbide/polylactic acid thermoelectric composites with favorable stability in air atmosphere, which has significant potential for flexible thermoelectric devices. Yu et al.162also proposed an AM process for carbon-nanotubes-based microsupercapacitors. The printed multi-layer carbon nanotubes and the PVA-H3PO4electrolyte solution were packaged as the final microsupercapacitors, which exhibited an excellent areal capacitance and cycle stability. Benefit from AM’s rapid development, 3D printed circuit board (PCB) has already realized commercialization. Fig. 26 shows complex multilayer PCBs fabricated via AM system. Recently, HENSOLDT utilized dielectric polymer ink and conductive ink developed by Nano Dimension to achieved the world-wide first 10-layer PCB with highperformance electronic structures soldered to both sides.

The integration of topology optimization and AM for complex multi-material functional system remains a promising and challenging topic, which holds considerable significance for structural and functional integrated components in engineering applications.

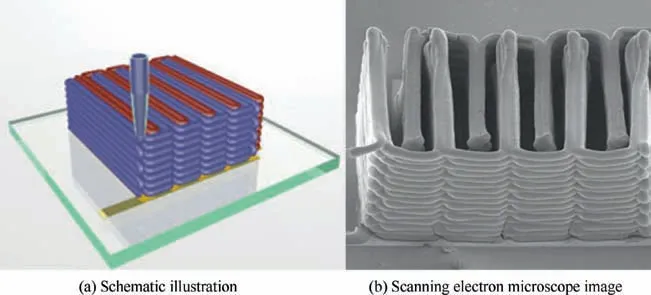
Fig. 25 3D printed interdigitated Li-ion micro-battery.160

Fig. 26 3D printed complex multi-layer PCBs (https://www.3dprintingmedia.network/electronics-additive-manufacturing/).

5. Conclusions

The deep integration of Topology optimization and AM is an efficacious approach to pursuing next-generation highperformance,multi-functional and lightweight structures.This article briefly recalls the structural optimization design methods for AM and corresponding applications in recent years.To cope the limitation of sequential structural design procedure, two primary topology optimization techniques for AM,i.e. structural design based on innovative configurations (e.g.lattice, hierarchical structures and stiffened thin-wall) and topology optimization based on AM constraints (e.g. length scale, connectivity and overhang constraints) are reviewed and summarized. Not only powerful and flexible manufacturing capabilities are fully exploited to accurately fabricate lattice and hierarchical structures with complex geometric configuration, but also topologically optimized structures can suffice AM design rules without additional structural adjustment in the reconstructing procedure.

Structural optimization for AM is and will be still a hot and attractive issue. And further researches need to be carried out to optimize and design practice industrial structures.This article also presents the current research challenges including characterizing accurately the performance of scale-related lattice structures with as little computational costs as possible, effect of AM process on material anisotropy and fatigue performance, and design and manufacturing of FGM and complex multi-material functional system. To cope these challenges,the further study directions should include the follows.

(1) How to systematically and accurately characterizes complex lattice structures especially surface-based lattice still requires further attention and study.And efficient modelling approach can promote hierarchical structural optimization to pursue higher performance.

(2) The prompt development of advance manufacturing technologies, e.g. multi-axis AM system163and additive and subtractive combined manufacturing technology,164,165further improve the manufacturing capability for complex structures. The emerging manufacturing technologies relax conventional AM’s constraints such as overhang constraints but yield new constraints and challenges. One of the challenges is how to efficiently program feasible sequence of material deposition or different process.163,165Integrating these new challenges into topology optimization to obtain more efficient design is a promising study direction.

(3) During AM procedure, material experiences complex thermal history which is affected by material properties,process parameters and structural configuration. Any variation of these factors makes an impact on the final product performance including mechanical performance and fatigue performance. Thus, developing an effective model to accurately predict product performance and considering it into structural optimization are important routes to realize the integrated design of material, process, structure and performance.

(4) Complex integral functional parts consisting multiple functional components and load-carrying structure can significantly decrease the number of parts(e.g.connectors)and shorten production cycle. How to pursue highperformance and lightweight integral functional parts via topology optimization and AM is a promising issue and possesses extensive engineering application prospects.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work is supported by National Key Research and Development Program (2017YFB1102800), Key Project of NSFC(51790171, 51761145111) and NSFC for Excellent Young Scholars (11722219).