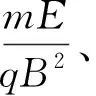非相对论下均匀斜交电磁场中正电荷的运动状况分析

邵 云，徐诗烨

(南京晓庄学院 电子工程学院，江苏 南京 211171)

目前已有不少学者对于非相对论下均匀斜交电磁场中正电荷的运动进行了研究，如文献[1-4]等，但是若从物理图像和便于理解的角度来说，仅有少数文献做到了这一点，如文献[1]等.多数文献(包括本文未引用的一些文章)均采用了求解微分方程组的方法，虽然求解并不复杂，但是其后续的物理分析却相当费力：图像不够清晰且不容易获得较全面的结论.此外，包括文献[1]在内的大多数文献的内容都显得不够完整，它们或者缺少系统的动力学分析[1]，或者缺少必要的计算过程、作图、分析探究等，甚至原理的阐述也存在错误[1].本文将总体沿袭文献[1]从物理图像上进行分析的思路，对均匀斜交电磁场中正电荷的运动状况进行更深入细致的研究，力求形成既形象又完整的认识.

1 正电荷在均匀斜交电磁场中的动力学分析

如图1所示，为便于分析与计算，设磁场B沿z轴正方向，电场E在yz平面内，与磁场方向成α夹角；并设开始时(t=0)点电荷+q位于坐标系的原点O处，初速度为v0(图中未画出).将E、v0分别在平行与垂直于磁场的方向进行投影，得

E=E//+E⊥

(1)

v0=v0//+v0⊥

(2)

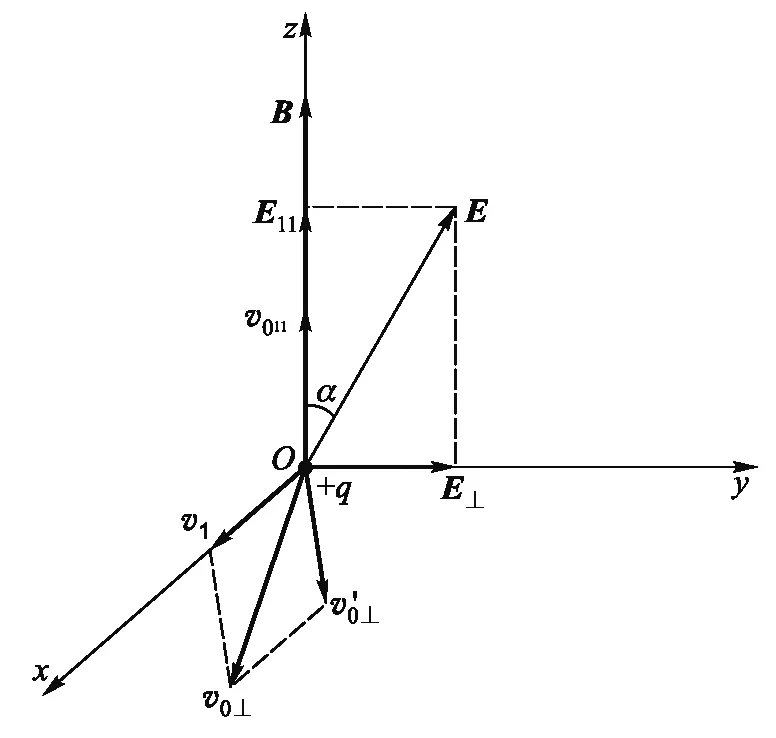
图1 均匀斜交电磁场中点电荷+q的初速度分解

设点电荷+q的质量为m，则它在图1所示均匀电磁场中的动力学矢量方程为

(3)

其中点电荷在任意时刻的速度矢量v亦可分解为

v=v//+v⊥

(4)

将式(1)、式(4)代入式(3)得

(5)

其中已考虑到v//×B=0.鉴于(v⊥×B)⊥B始终成立，因此式(5)可分解为

(6)

(7)

式(6)意味着点电荷+q沿磁场方向做匀加速直线运动.对于式(7)，可设计一个沿x轴正方向的恒定速度v1，如图1中所示，使得

E⊥+v1×B=0

(8)

易见v1的大小为

(9)

于是式(7)可修改为

(10)

再设

v′⊥=v⊥-v1

(11)

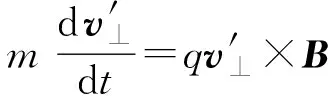
(12)

显然，v′⊥表达的是一个在洛伦兹力的作用下在xy平面内的匀速率圆周运动，如图2所示.至此，我们已将速度矢量v分解成

v=v//+v⊥=v//+v1+v′⊥

(13)

即将点电荷+q在电磁场中的运动分解为：沿磁场B方向的匀加速直线运动，见式(6)；沿x轴方向速度为v1的匀速直线运动；xy平面内的匀速率圆周运动，见式(12).

图1和2中已标出匀速率圆周运动速度v′⊥的初矢量v′0⊥，它不仅依赖于电荷的初速度v0(或v0⊥)，还依赖于引入速度v1，可称之为xy平面内的“相对初速度”.若设v0=v0xi+v0yj+v0zk，结合图1、图2，便得速率：

(14)

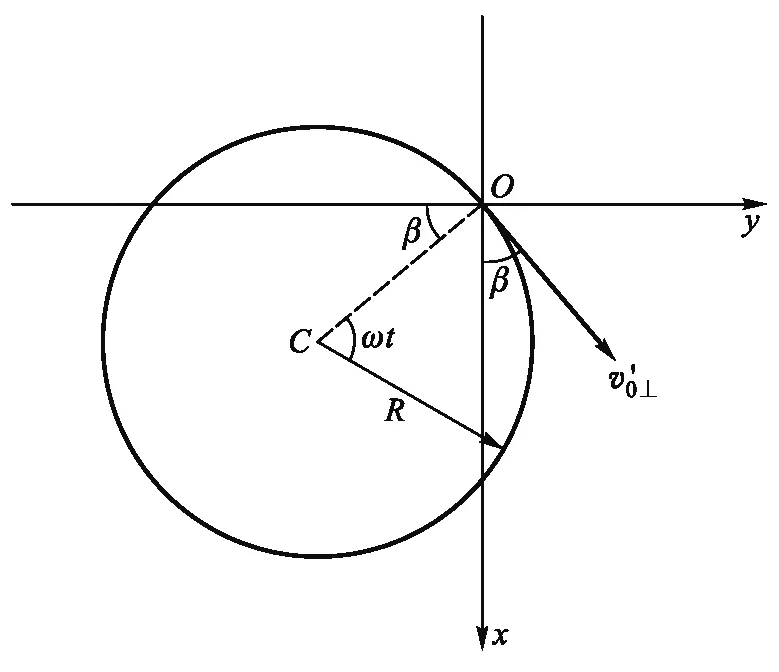
图2 点电荷+q在xy平面内的分运动之一——匀速率圆周运动

以及v′⊥与x轴正方向的初始夹角：

(15)

2 正电荷在均匀斜交电磁场中的运动学方程

根据速率表达式(14)可得图2中匀速率圆周运动的半径为

(16)

圆频率为

(17)

圆心C的坐标为

xC=Rsinβ

(18)

yC=-Rcosβ

(19)

设点电荷+q在任意t时刻的实际空间坐标为(x,y,z)，结合初始条件及图1，由式(6)可得点电荷在z方向上的运动方程为

(20)

结合初始条件及图2，由式(11)又可得点电荷在xy平面内的运动方程为

x(t)=v1t+xC+Rsin(ωt-β)

(21)

y(t)=yC+Rcos(ωt-β)

(22)

这里需要说明一下，点电荷在xy平面内的初速度分量v0x、v0y已融入圆周运动诸参量，故而它们未在式(21)、(22)中显现.将式(9)、(15)—(19)代入式(21)、(22)，整理可得

(23)

(24)

式(20)、(23)、(24)便构成了点电荷+q在均匀电磁场中的整个空间运动方程.

倘若点电荷+q的初速度v0=0，则运动方程式(20)、(23)、(24)分别简化为

(25)

(26)

(27)

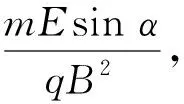
3 正电荷在xy平面内的投影运动轨迹及分析

鉴于点电荷+q在磁场方向也即z轴方向做简单而独立的匀加速直线运动，见式(20)，因此我们只需考察它在xy平面内的投影运动，即可了解不同初速度情形下各种运动的差别.

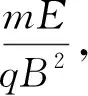
(28)

(29)

下面将取不同的初速度分量v0x、v0y(单位为E/B)分别讨论点电荷在xy平面内的投影运动轨迹.

1)v0x=0，v0y=0

这实际上是电荷的初速度沿磁场方向的情形，此时式(28)、(29)简化为

x(t)=0.5(t-sint)

(30)

y(t)=0.5(1-cost)

(31)

正如上文所言，此时电荷在xy平面内的轨迹为一圆滚线，如下文图3所示.

2)v0x=v1=0.5，v0y=0

这时电荷在xy平面内的初速度恰为v1，式(28)、(29)简化为

x(t)=0.5t

(32)

y(t)=0

(33)

显然，这时电荷在xy平面内因受力平衡而沿x轴做速度为v1的匀速直线运动.

3)v0x=1.5v1=0.75，v0y=0

这时式(28)、(29)简化为

x(t)=0.5t+0.25sint

(34)

y(t)=-0.25(1-cost)

(35)

4)v0x=0.5v1=0.25，v0y=0

这时式(28)、(29)简化为

x(t)=0.5t-0.25sint

(36)

y(t)=0.25(1-cost)

(37)

5)v0x=2v1=1，v0y=0

这时式(28)、(29)简化为

x(t)=0.5(t+sint)

(38)

y(t)=-0.5(1-cost)

(39)

可见此时电荷在xy平面内的轨迹也是一圆滚线，形状与1)情形相同.

6)v0x=-v1=-0.5，v0y=0

这时电荷在xy平面内的初速度沿x轴负方向，式(28)、(29)简化为

x(t)=0.5t-sint

(40)

y(t)=1-cost

(41)

这时电荷在xy平面内的初速度沿y轴正方向，式(28)、(29)简化为

(42)

(43)

8)v0x=v1=0.5，v0y=2v1=1

这时电荷在xy平面内的初速度沿0.5i+j方向，式(28)、(29)简化为

x(t)=0.5t+1-cost

(44)

y(t)=sint

(45)

将上面1)～6)6种情形下电荷在xy平面内的轨迹一同绘于图3，而将6)～8)3种情形(v′0⊥相等)下的轨迹绘于图4.

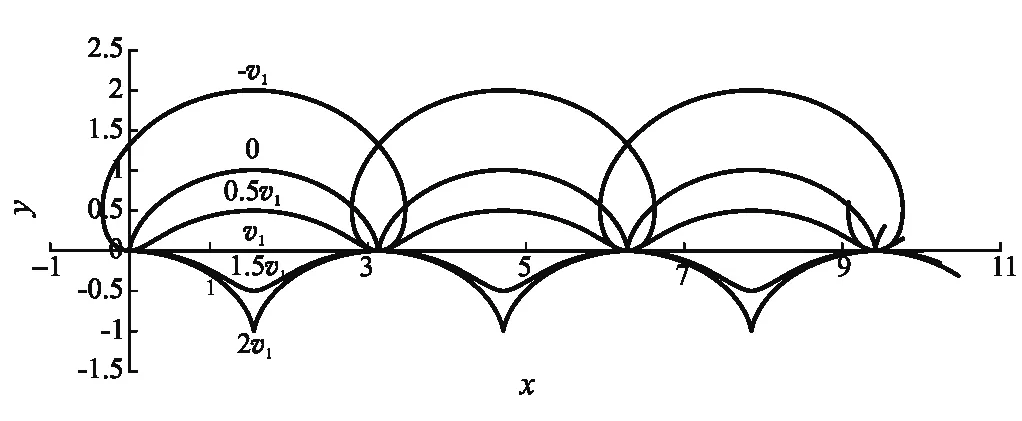
图3 v0y=0而v0x取几个典型值时点电荷+q在xy平面内的投影运动轨迹

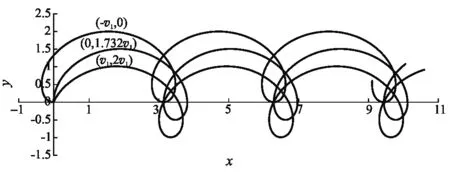
图4 v′0⊥相同而v0x、v0y取不同值时点电荷+q在xy平面内的投影运动轨迹

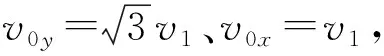
图3中的短幅圆滚线、圆滚线、长幅圆滚线轨迹分别对应于“相对初速度”大小也即圆周运动速率v′0⊥v1这三种情形，其中原因不言而喻.

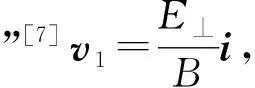
(46)

式(46)右边()内便是上文所述长度单位，因此图3、图4中共同周期Δx的数值为π.

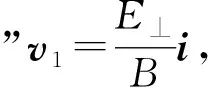
4 正电荷的空间运动轨迹

根据运动方程式(20)、(23)、(24)可作出点电荷+q在空间的运动轨迹.为了一般起见，取初速度分量v0x=v0y=v0z=2v1=1 (E/B)作为特例，α依然取30°，则上述运动方程式可“约化”并简化为

(47)

x(t)=0.5t+0.5sint-cost+1

(48)

y(t)=0.5cost+sint-0.5

(49)

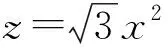
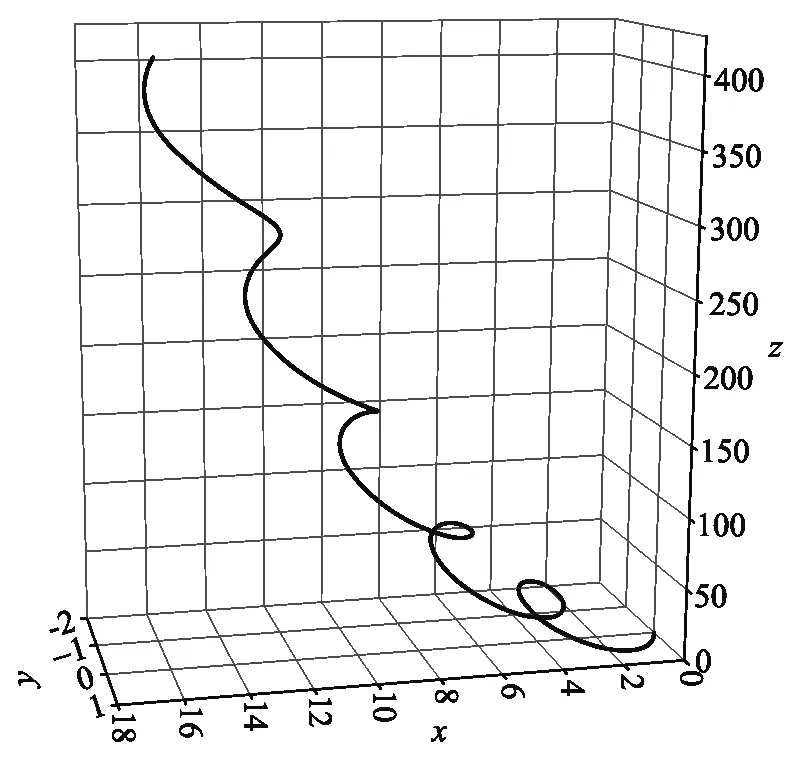
图5 初速度分量取v0x=v0y=v0z=2v1=1 (E/B)时点电荷+q 的空间轨迹

(50)

由第3节的结论可知，除了初速度分量v0x=v1=0.5 (E/B),v0y=0的情形下电荷的空间轨迹是2维曲线外，其他初速情形下的空间轨迹皆与图5中类似.

5 关于均匀正交电磁场(E⊥B)情形下3种特殊情况的讨论

对于常见的均匀正交电磁场情形，参见图1，有α=90°，则式(20)、(23)、(24)约简为

z(t)=v0zt

(20′)

(23′)

(24′)

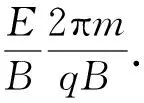
5.1 E⊥B,v0//E的情形

此时有v0x=v0z=0,v0y=v0，将其代入式(20′)、(23′)、(24′)，化简可得

(51)

按照第3节中的分析，由于这时图1中的“相对初速度”也即图2中的圆周运动速率

由图3、图4可知，此时点电荷+q的空间轨迹与图4中标记为(0,1.732v1)的投影轨迹类似，均为xy平面内的长幅圆滚线.

5.2 E⊥B, v0//B的情形

此时有v0x=v0y=0,v0z=v0，将其代入式(20′)、(23′)、(24′)，化简得

(52)

其中后两分式其实就是上文第2节中式(26)、(27)令α=90°.于是可见，点电荷+q在xy平面内做类似于图3中标记为0的严格圆滚线运动，在z轴方向则做v0速度的匀速运动.

5.3 E⊥B, v0//(E×B)的情形

此时有v0x=v0,v0y=v0z=0，代入式(20′)、(23′)、(24′)整理得

(53)

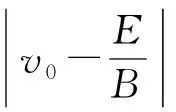
本节的内容在文献[3]中曾有类似的讨论，结果一致.虽然本节运动方程式(51)—(53)都比较简单，并且通过观察也能发现电荷在xy平面内的运动是两种运动的叠加[7]，但是其中的物理机制、图像却不甚明朗，仍需借助第1—3节中的分析结论(包括图1—4)来阐述.

6 总结与说明

不同于多数文献所采用的直接求解微分方程组的思路，本文采用的是速度矢量分解和代换的分析方法，将点电荷+q在均匀斜交电磁场中的运动分解为：沿磁场方向的匀加速直线运动;垂直于电、磁场方向的匀速直线运动;垂直于磁场方向的匀速率圆周运动，进而分析得到电荷的运动方程.该方法物理图像清晰，容易掌握，更便于后续的运动状况分类及分析，见本文第3节.

本文引入代换式(11)即v⊥=v1+v′⊥，将电荷在xy平面内的投影运动进行分解的物理本质是：采用速度为v1的平动参考系来平衡电场力E⊥q，消去E⊥的影响[8]，于是就只剩下图2中洛伦兹力作用下的匀速率圆周运动了.