平行板电容器的尺寸效应
曹小鸽,杨 杨
(1. 西安交通大学城市学院 电信系,陕西 西安 710018;2. 西安交通大学城市学院 物理教学部,陕西 西安 710018)
对于真空中的极板面积为S、极板间距为d的平行板电容器,教科书中给出的电容公式为
(1)
其中的ε0是真空电容率.在推导这个公式时,需假定两个极板相距很近,忽略其边缘效应,将两个极板近似为无限大带电平面,两个极板之间形成的是匀强电场,从而得到式(1).但实际的平行板电容器的大小终究是有限的,极板间的电场也并不是理想的匀强电场,故其电容和C0会有一定的偏差.目前计及边缘效应的平行板电容器的研究已有很多.文献[1-3]研究了一边有限宽、另一边无限长的长方形极板的情形,文献[4,5]则研究了正方形极板的情形,这些研究均基于Schwarz-Christoffel变换.文献[6]用有限元仿真的方法研究了圆极板的情形,文献[7]也给出了少量的数值结果.本文分别对圆形极板和矩形极板的平行板电容器做了近似计算与有限元仿真,研究其电容随尺寸大小变化的规律,即所谓尺寸效应.
1 平行圆形板电容器的尺寸效应
考虑一个真空中的平行圆形板电容器,极板半径为R,极板间距为d.建立如图1所示的坐标系,下极板在xy平面内,原点为下极板的中心,上极板在z=d平面内,z轴为两极板的中轴线.
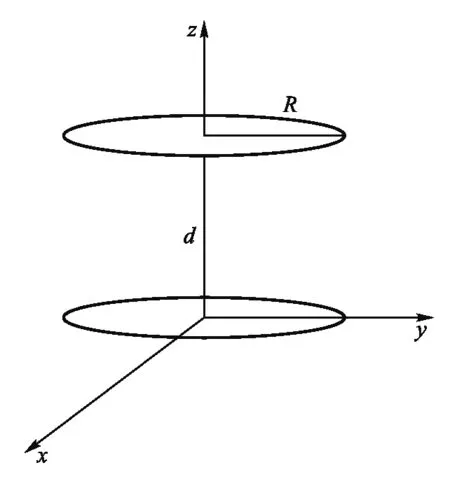
图1 平行圆形板电容器
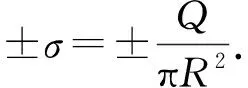
(2)
带负电的上极板在中轴线上产生的场强方向也沿着z轴的正方向.若场点距下极板为z,则其距上极板为d-z,根据场强叠加原理,两极板间中轴线上z处的总场强为
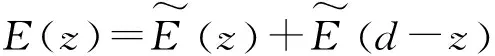
(3)
将场强沿中轴线积分,可得两极板间的电势差为
(4)
根据定义,平行圆形板电容器的电容为
(5)
将分母有理化,整理可得
(6)
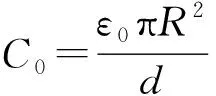

图2 平行圆形板电容器的f随d/R变化的曲线
注意,式(6)是根据电荷在极板上均匀分布这一假设而导出的.实际上,由于边缘效应,电荷不可能是严格的均匀分布,式(6)仍然是一个近似的结果.接下来我们用Ansoft软件进行仿真,并将结果与式(6)比较.设定圆形极板的半径R=50 mm,厚度为0.1 mm,材质为铜,两极板上所带电荷分别为±1×10-5C,极板间为真空.给定极板间距d后,即可用有限元法算出两极板间的场强分布和电势分布,进而得到两极板间的电势差,最终根据定义求出实际电容.我们改变极板间距d,算出相应的电容,将结果绘制到图2中(○号).文献[7]中给出了圆形板电容器的5组数据,也绘制到图2中(△号)作为参考.此外,圆形板电容器的电容还可用克希霍夫公式[4]近似描述,即
(7)
我们也将相应结果绘制到图2中(虚线).可见,当d/R较小时,仿真结果与文献[7]的数据以及克希霍夫公式符合得很好.仿真结果表明,f确实随d/R的增大而增大,其数值比均匀带电近似的结果为大.通过比较可知,我们采用均匀带电近似导出的结果能正确地反映电容随尺寸变化的趋势,较之C0更为精确,但与实际电容相比仍偏小.当d/R较小时,均匀带电近似的精度不及克希霍夫公式;当d/R大到一定程度后,均匀带电近似的精度会优于克希霍夫公式.
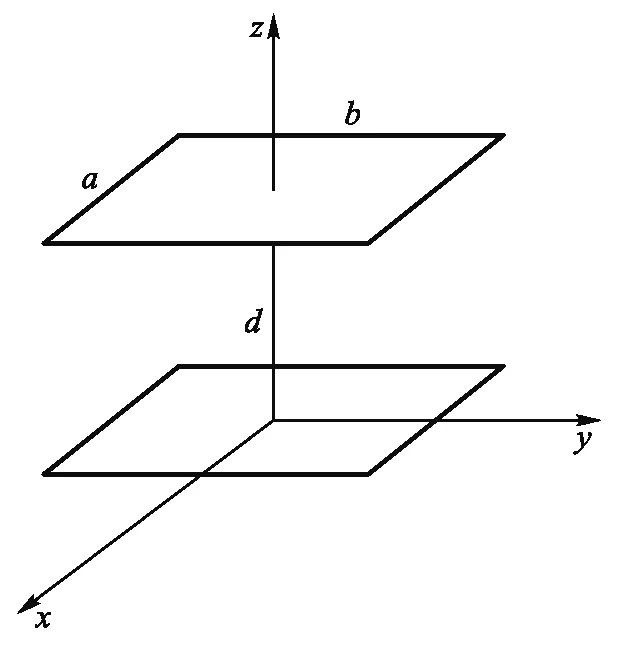
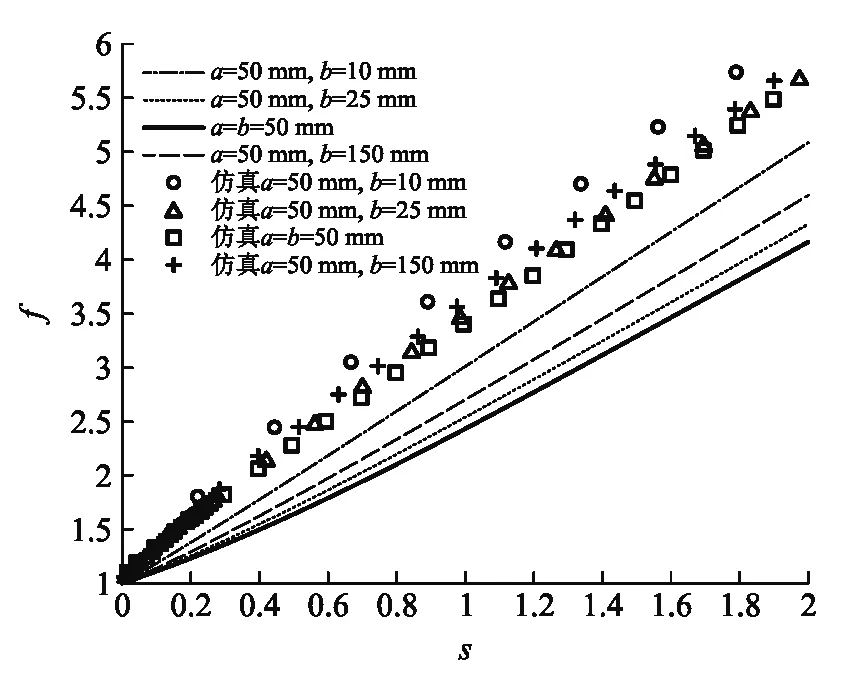
图3所示是d=30 mm时圆极板内侧表面附近的场强E随极板半径r的变化关系,而表面附近的场强和极板上的电荷面密度成正比,所以曲线也反映了电荷面密度的变化趋势.根据图3所示,在r<35 mm的区域内,电荷近似为均匀分布;在35 mm 图3 圆极板内侧表面附近的场强随极板半径的变化关系 考虑一个平行矩形板电容器,矩形极板的两个边长分别为a和b,极板间距为d.建立如图4所示的坐标系,下极板在xy平面内,x轴和y轴分别与下极板的两条边平行,原点在下极板的中心,上极板在z=d平面内,z轴为两极板的中轴线. 图4 平行矩形板电容器 (8) 带负电的上极板在中轴线上的场强方向也沿z轴正方向.和圆极板的情形类似,根据场强叠加原理,两极板间中轴线上z处的场强为 (9) 将场强沿中轴线积分,可得两极板之间的电势差为 (10) 根据定义,可求出平行矩形板电容器的电容为 (11) (12) 这个积分无法求出解析形式,只得作数值计算.矩形极板的对称性不及圆形极板,我们定义这样一个无量纲的相对尺寸参数: (13) 图5 平行矩形板电容器的f随s变化的曲线 注意,式(12)是一个无量纲的积分,其中的被积函数是关于x′和y′对称的,把参数s代入该式的两个积分上限可得 (14) 由于边缘效应,电荷在极板上不可能是严格的均匀分布,式(11,12)只是近似的结果.接下来我们用Ansoft软件进行仿真,并与均匀带电近似的结果比较.我们把矩形极板的边长分别设定为均匀带电近似中的4组数值,极板厚度为0.1 mm,材质为铜,两极板上所带电量为±1×10-5C,极板间为真空.我们改变极板间距d,求出相应的电容,将结果绘制于图5中.仿真结果表明,f确实随s的增大而增大,其数值比均匀带电近似的结果为大,而且仍然是c越大的曲线越低.通过比较可知,我们采用均匀带电近似导出的结果能正确地反映电容随尺寸变化的趋势,较之C0更为精确,但与实际电容相比仍偏小.实际电容较大的原因在于极板上的电荷分布中间少、边缘多,和圆极板的情形是类似的. 本文研究了平行圆形板和矩形板电容器的电容随其尺寸变化的规律.我们一方面假设极板上的电荷均匀分布作近似计算,另一方面用Ansoft软件作有限元仿真,并将两种结果进行对比.均匀带电近似的计算较简便,而且能够正确地反映电容的变化趋势,尤其是圆形板情形还得出了解析式.有限元仿真得到的电容更大,原因在于极板上的电荷分布中间少、边缘多.本文的结果对静电场部分的教学有参考价值,对平行板电容器的制作也有一定的理论指导意义.
2 平行矩形板电容器的尺寸效应

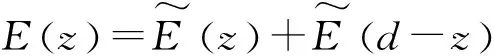
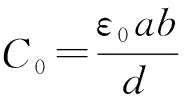
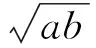

3 结论

