不同冷却工况下的磨削钛合金温度场模型及验证
王晓铭 张建超 王绪平 张彦彬 罗 亮 赵 伟 刘 波 聂晓霖 李长河
1.青岛理工大学机械与汽车工程学院,青岛,266520
2.迈赫机器人自动化股份有限公司智能制造技术研究院,潍坊,262200
3.宁波三韩合金材料有限公司,宁波,315040
4.烟台海英机械有限公司,烟台,265299
5.四川明日宇航工业有限责任公司,什邡,618400
6.南京科润工业介质股份有限公司,南京,211106
0 引言
钛合金磨削加工中,高温和高应力导致的低表面质量和砂轮磨损是限制其进一步工程化应用的技术瓶颈[1-2]。传统磨削加工普遍采用冷却液浇注式供给实现润滑和冷却,然而,高昂的处理费用和环境、健康危害违背了可持续制造的发展理念[3]。干磨削是在磨削过程中不使用冷却润滑介质的一种加工方式,避免了切削液带来的危害,但是由于缺少冷却和润滑,工件表面烧伤与砂轮磨损严重[4]。微量润滑是将润滑介质雾化、以微液滴的形式喷射至磨削区,降低了砂轮磨粒/工件的摩擦磨损,得到较好的工件表面质量[5]。通过微量润滑供给系统将纳米流体(高热导率的固体纳米粒子与基础润滑介质的混合物)喷射至砂轮/工件界面,可以大幅提高基液的抗磨减摩能力与换热性能[6-8]。笔者将低温风冷与纳米流体微量润滑方式相结合,提高了冷却介质在磨削区的强化换热能力,降低了工件的表面温度。
国内外学者对不同冷却工况下的磨削温度预测模型开展了广泛研究。ANDERSON等[9]研究了基于不同热源模型的干式浅磨削和深磨削的磨削温度场有限元模型。HADAD等[10]建立了磨削液浇注式对流换热冷却的二维瞬态热传导有限元模型。毛聪等[11]通过有限元仿真研究了工件表面热载荷改变对工件表面温升的影响,依据微量润滑雾化机理对磨削区传热系数数学模型开展了研究[12]。YANG等[13]对不同冷却条件下的微尺度颅骨磨削温度场进行研究,建立了微磨削下的热流密度模型、对流传热系数模型和工件内热传导模型。然而,新工艺的换热机制引起的边界条件改变使得上述模型并不能满足低温风冷纳米流体微量润滑沸腾换热工件表面温度精准预测的需求。
笔者将抗磨减摩性能优异的纳米流体微量润滑与换热能力良好的低温风冷相结合,在保证磨削界面润滑的前提下,提高冷却介质的热交换能力,降低工件表面温度。同时,基于沸腾换热的四个阶段,建立了三种冷却方式下的温度场模型,并开展了磨削温度场的数值仿真与实验验证。
1 平面磨削温度场模型
1.1 磨削区热量分配
图1所示的平面磨削中,磨削工件输入的能量作用于磨削区所产生的总热流密度为[14]
(1)
(2)
式中,P为功率,W;A0为磨削接触面积,mm2;Ft为切向磨削力,N;vs为砂轮的圆周速度,m/s;lc为工件和砂轮的接触弧长,mm;b为磨削宽度,mm;ds为砂轮当量直径,mm;ap为磨削深度,μm。
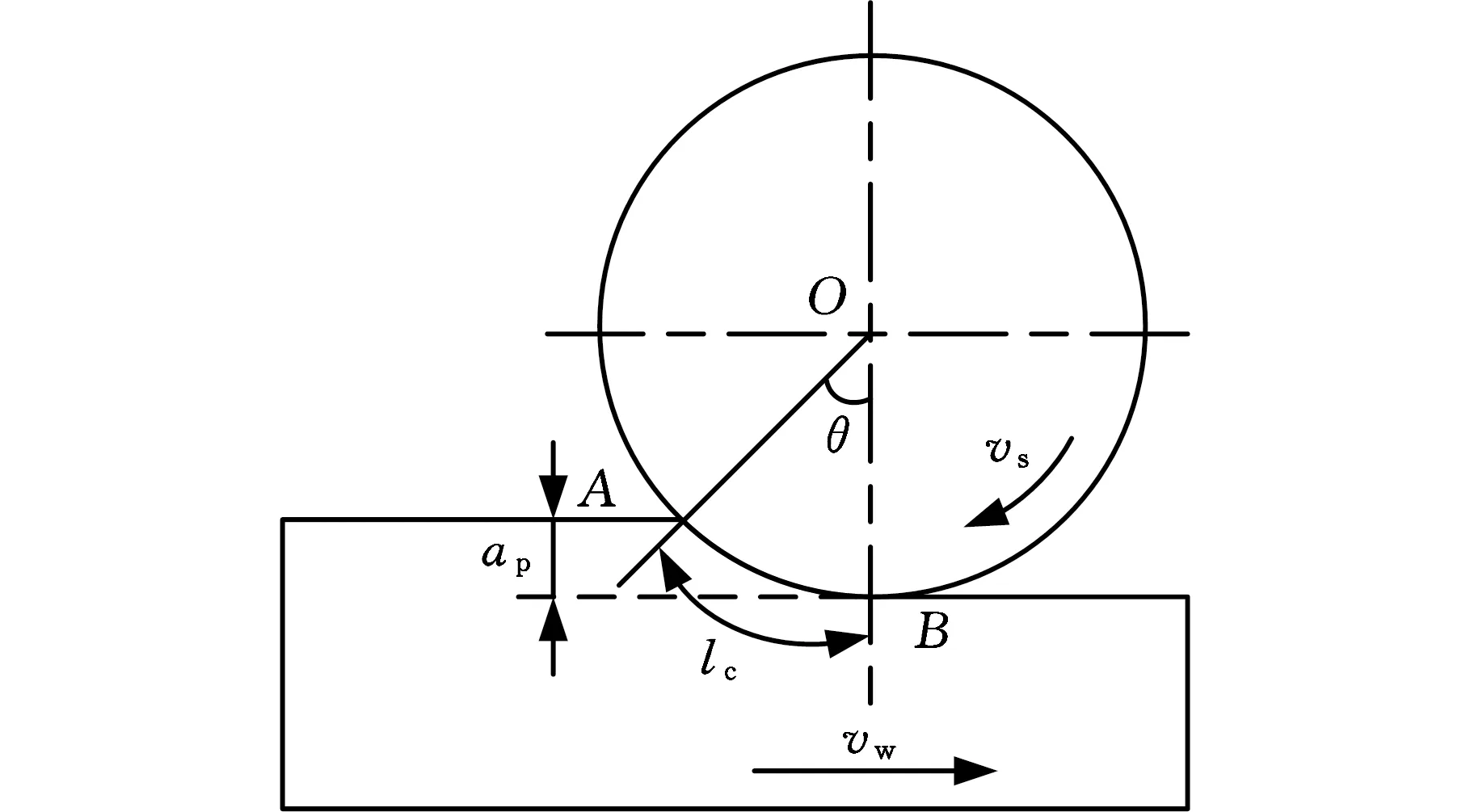
图1 磨削接触模型
磨削产生的热量将分散至工件、磨屑、磨粒、环境空气与磨削液,定义能量比例系数R为传入工件的热量与磨削总热量的比值。在有切削液参与的情况下,进入磨削区的切削液会在砂轮/工件界面间形成一层液膜,将传入液膜的热量归为分散至砂轮的热量,由此得到的能量比例系数为
(3)
式中,λ为热导率,W/(m·K);ρ为密度,g/cm3;v为速度,m/s;c为比热容,J/(kg·K);下标g、w、f、s分别表示砂轮磨粒、工件、润滑基液、砂轮;Ar为砂轮与工件的实际接触面积;A为名义接触面积。
将纳米粒子添加到冷却介质后,冷却介质的换热性能会显著提高,由式(3)可以得到纳米流体微量润滑磨削下的能量比例系数:
(4)
式中,φ为纳米粒子的体积分数;下标n代表纳米粒子。
根据不同的磨削深度可将磨削热源模型分为矩形分布热源、三角形分布热源、圆弧分布热源。小切深和光整加工中,切削深度小,磨削接触弧长比磨削宽度小,热源模型为矩形分布热源。随着磨削深度逐渐增大,接触弧长增大,热源强度在接触弧上不再均匀分布,可将磨削区看作无限个沿接触区不断增大的三角形分布热源。在缓进磨削和高效深磨等大切深(切深为0.1~30 mm)磨削加工中,磨削深度与接触弧长进一步增大,流入工件的热流密度沿热源面呈抛物线分布[15]。在本研究中,切削深度为10 μm,需要充分考虑热源强度在接触弧长的非均匀分布,综合上述三种热源的使用范围,本研究采用图2所示的三角形分布热源[16]。
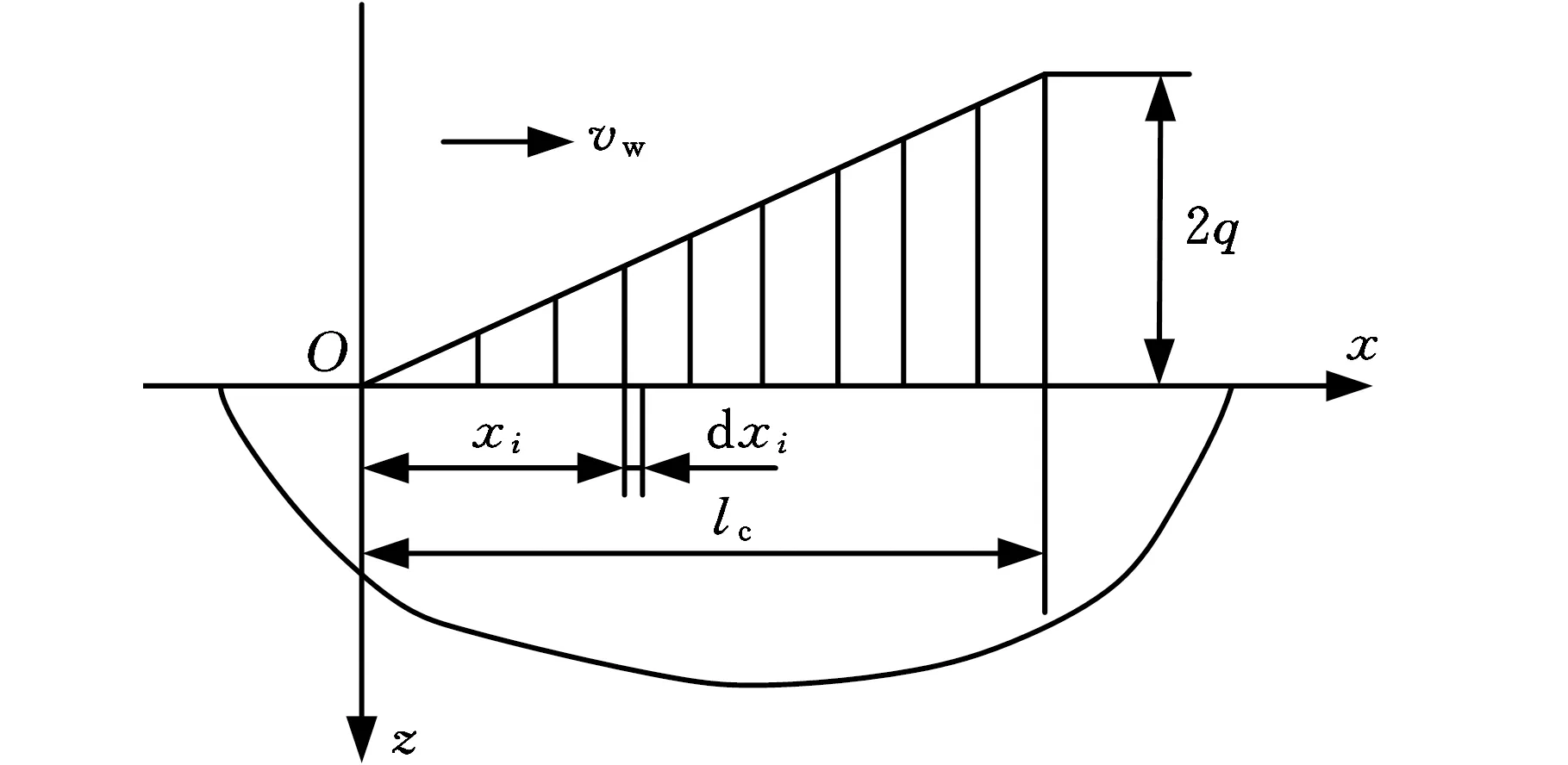
图2 三角形分布热源
热源内点xi的热源强度q(xi)可表示为
q(xi)=2q(1-xi/lc)
(5)
式中,q为流入工件的平均热流密度,W/m2。
如图3所示,磨削温度场的建立需要综合考虑磨削区热分配比例系数模型、冷却介质传热系数模型、工件材料内部热传导微分方程,以及初始条件、边界条件。

图3 温度场建模路线
1.2 磨削温度场传热系数模型
传热系数是表征冷却介质在磨削区热交换能力的最直接参数。低温风冷方式没有液体冷却介质,不产生沸腾换热,换热为冷空气与工件表面的强化对流换热。强化对流换热中对流传热系数ha为
ha=λaNu/l
(6)
Nu=0.906Re1/2Pr1/3
Re=vaρal/μaPr=μaca/λa
式中,λa为气体热导率,W/(m·K);Nu为努赛尔数;Re为雷诺数;Pr为普朗特数;va为空气的流动速度;ρa为空气的密度,kg/m3;μa为空气的动力黏度,Pa·s;ca为空气的等压比热容,J/(kg·K);l为磨削区换热宽度,mm。
纳米流体微液滴输运至砂轮/工件界面后,受磨削区高温的影响,微液滴温度迅速升高,甚至超过基础油的沸点。当沸点温度与工件表面温度差ΔT超过最小过热度ΔTs时,换热状态转变为沸腾换热。沸腾换热包括四个阶段:自然对流、核态沸腾、过渡沸腾和膜态沸腾[12]。由下式[17]可以确定微液滴所处的换热阶段:
(7)
(8)
式中,σ为表面张力,N/m;r为凹液面半径,mm;Ts为饱和温度,℃;B0为常数;ΔTmin为膜态沸腾换热的最小过热度,℃;Kg为气膜传热系数,kW/(m·s·K);g为重力加速度,m/s2;ζ为潜热,kJ/kg;ρg为气膜密度,kg/m3;pl为液体密度,kg/m3;μl为液体动力黏度,Pa·s;ps为饱和蒸汽压力。
1.2.1自然对流阶段的沸腾传热系数
工件表面温度与微量润滑基油沸点的差值小于最小过热度时,换热以对流换热为主。冷却介质通过微量润滑装置喷射到产热区时,单个液滴的铺展半径为[18]
(9)
式中,Vl为单个雾滴的体积,m3;θn为接触角,(°);d0为雾滴的直径,μm。
依据YANG等[19]针对无沸腾传热系数的研究可知:
(10)
式中,Nl为所喷射出的雾滴数量,Nl=qV/V1;qV为磨削过程冷却介质供给量,μm3/s;t为磨削过程总时间,t=a/vw;a为工件的长度,μm;vw为工件的进给速度,μm/s;hn1为无沸腾传热系数;cl为液滴比热容,J/(kg·K);h′a为空气的常温对流传热系数,W/(m2·K);ρl为纳米流体的密度,kg/m3。
1.2.2核态沸腾与过渡沸腾阶段的沸腾传热系数
ΔTs<ΔT<ΔTs+50 ℃时,冷却介质处于核态沸腾换热阶段;ΔTs+50 ℃<ΔT<ΔTmin时,冷却介质处于过渡沸腾换热阶段。在临界热流密度点,传热系数会达到峰值[20]:
(11)
式中,hfa为汽化潜热,kJ/kg;Tl为纳米流体的温度,K;Tn2为核态沸腾末点温度。
1.2.3过渡沸腾与膜态沸腾阶段的沸腾传热系数
工件表面温度与微量润滑基油沸点的差值大于膜态沸腾换热的最小过热度ΔTmin时,纳米流体换热进入膜态沸腾换热阶段,膜态沸腾起始点处的传热系数为[20]
(12)
式中,We为韦伯数;vn为雾滴撞击换热面的垂直速度;pa为雾化喷嘴的压力,Pa;po为大气压力,Pa;ε为辐射系数;Tne为壁面温度;λv为蒸气的热导率,W/(m·K);cv为蒸气的比热容,J/(kg·K);μv为蒸气的动力黏度,Pa·s。
沸腾换热传热系数的求解需确定微液滴的热-物理属性:Ts=105 ℃,σ=2.02×10-2N/m,ps=0.1 MPa,Vl=2.14×10-12m3,θn=51.86°,d0=160 μm,Nl=7800,qV=2.2×1010μm3/s。cl=1870 J/(kg·K),h′a=278 W/(m2·K),ρl=665 kg/m3,rsurf=1.2×10-4m,hfa=384.3 kJ/kg,Tl=1.2 ℃,Tn2=157.4 ℃,vn=10.8 m/s,po=110 kPa,pa=600 kPa,λv=0.026 24 W/(m·K),μv=0.018 448 Pa·s,cv=1004 J/(kg·K)。不同工件表面温度对应的传热系数如图4所示,传热系数最大值对应临界热流密度点。
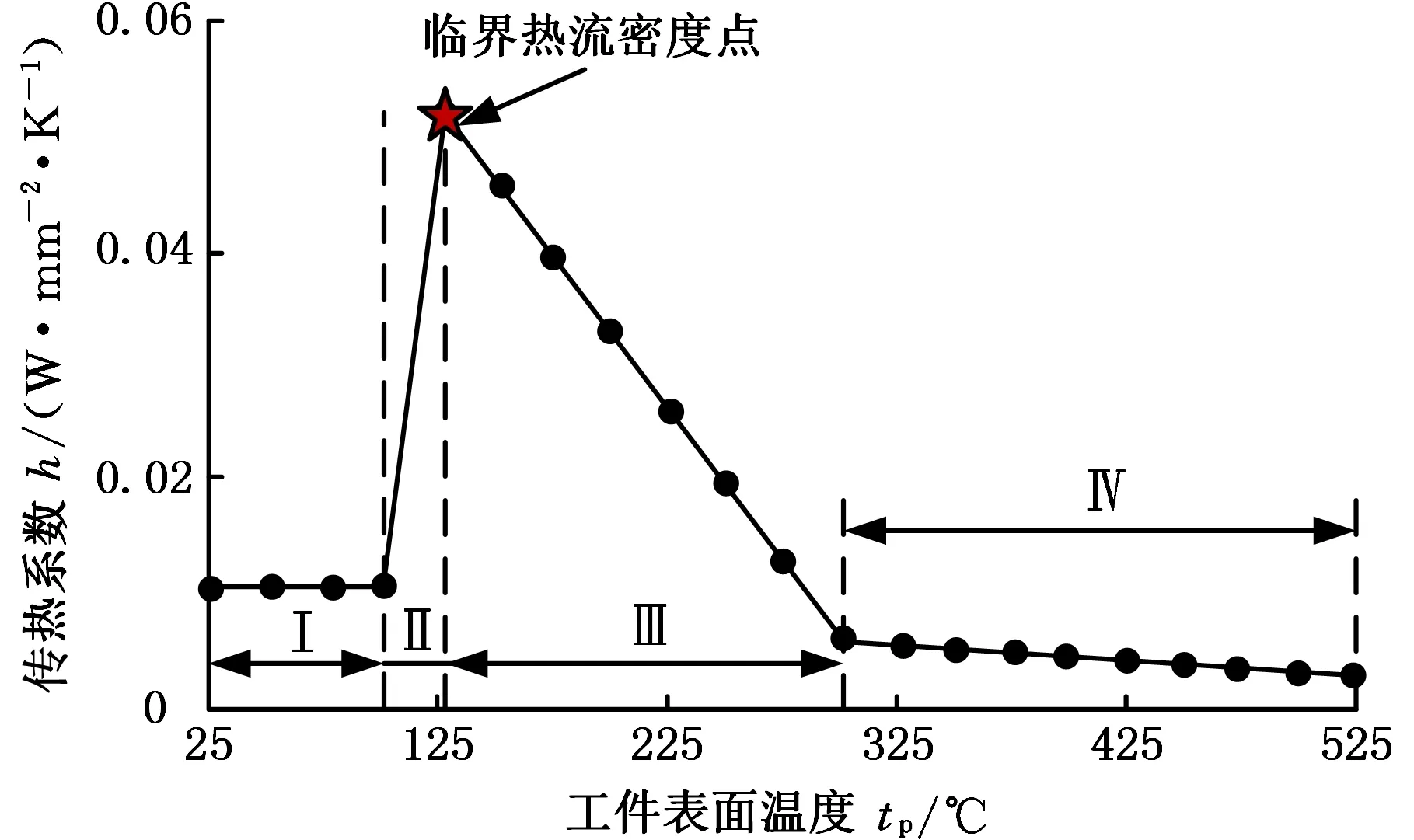
Ⅰ.自然对流 Ⅱ.核态沸腾 Ⅲ.过渡沸腾 Ⅳ .膜态沸腾
得到3种冷却方式下换热状态各阶段端点的传热系数后,依据图4所示各阶段传热系数的变化规律,代入工件表面温度即可求出各冷却方式的传热系数,如表1所示。
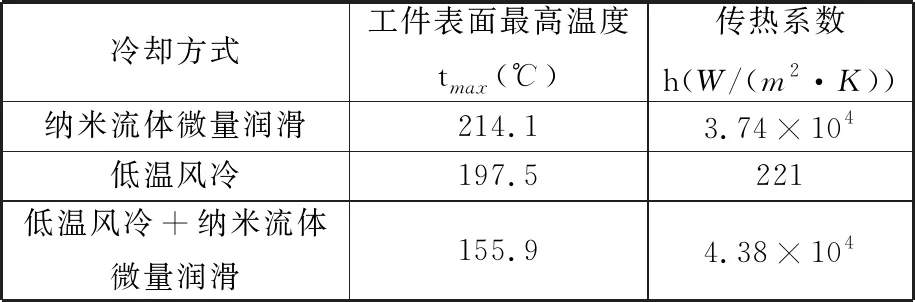
表1 三种工况工件表面温度及传热系数
1.3 磨削温度场数学模型
1.3.1热传递模型
热源在砂轮轴向分布均匀,假设砂轮轴向无热交换,因此,磨削温度场可简化为二维传热。依据傅里叶传热定律及热力学第一定律,建立二维无内热源瞬态温度场的热平衡微分方程[21]:
(13)
式中,T为工件的瞬态温度,℃;Kp为工件的传热系数,W/(m2·K);α为热扩散率,m2/s。
1.3.2建立差分方程
利用有限差分法将二维矩形工件离散为图5所示的均匀平面网格,网格的长和宽均为Δl。节点的温度代表所属网格的温度。选取任一点(i,j),依据热力学第一定律,该节点将与其相互接触的节点发生热传导,在热传导达到平衡时,达到稳定温度。

图5 均匀平面网格
建立以二阶差商为基础的有限差分方程组:
(14)
式中,T(i,j)为点(i,j)的温度;Tt+Δt(i,j)为点(i,j)在t+Δt时刻的温度;Δt为时间增量;O(*)为无穷小量。
将式(14)代入二维热传导方程,得到各网格节点处的差分方程:

(15)
1.3.3温度场边界条件
选取工件上的点(i,1)分析边界条件。如图6所示,磨削过程中,工件与砂轮的接触界面各节点之间的热传递、热量输入、节点自身温升,以及工件磨削表面与冷却介质、环境空气的换热遵守能量守恒定律:
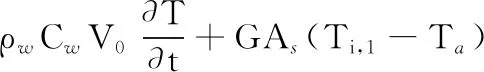
(16)
G=[1/h+ΔZ/(2Kp)]-1
(17)
q(i-1,1)→(i,1)=Kp(T(i-1,1)-T(i,1))
(18)
q(i+1,1)→(i,1)=Kp(T(i+1,1)-T(i,1))
(19)
q(i,2)→(i,1)=Kp(T(i,2)-T(i,1))
(20)
式中,G为综合传热系数;Ta为冷却介质的温度;T(i,1)、T(i-1,1)、T(i+1,1)、T(i,2)分别为点(i,1)、(i-1,1)、(i+1,1)、(i,2)的温度;V0为单个网格的体积;As为单位网格的表面积;ΔZ为网格宽度。
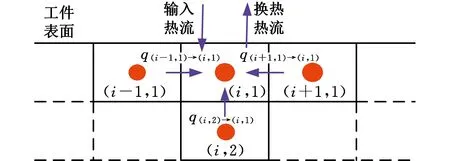
图6 点(i,1)的热传递状态
将式(18)~式(20)代入式(9),得出经过时间Δt后,点(i,1)的温度:
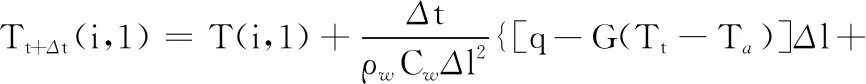
(21)
同理,可以通过热量平衡方程求解其他边界温度。
2 实验材料与方法
2.1 实验设备
实验采用K-P36精密数控平面磨床、SiC砂轮(外径300 mm、宽度20 mm、内径76.2 mm)。如图7所示,纳米流体通过上海金兆节能科技有限公司的微量润滑供给装置KS-2106输运并经喷嘴雾化喷射至磨削区,VC62015G型涡流管为低温冷风供给设备。采用JC2000C1B接触角测量仪对纳米流体的接触角进行测量,测量原理如图8所示,采用DN15型涡街流量计测量气体流量,采用YDM-Ⅲ99三向磨削测力仪记录和测量磨削力,采用MX100型热电偶测量和记录温度,采用夹式热电偶测量工件表面温度,测量方式如图9所示。

(a)微量润滑供给设备
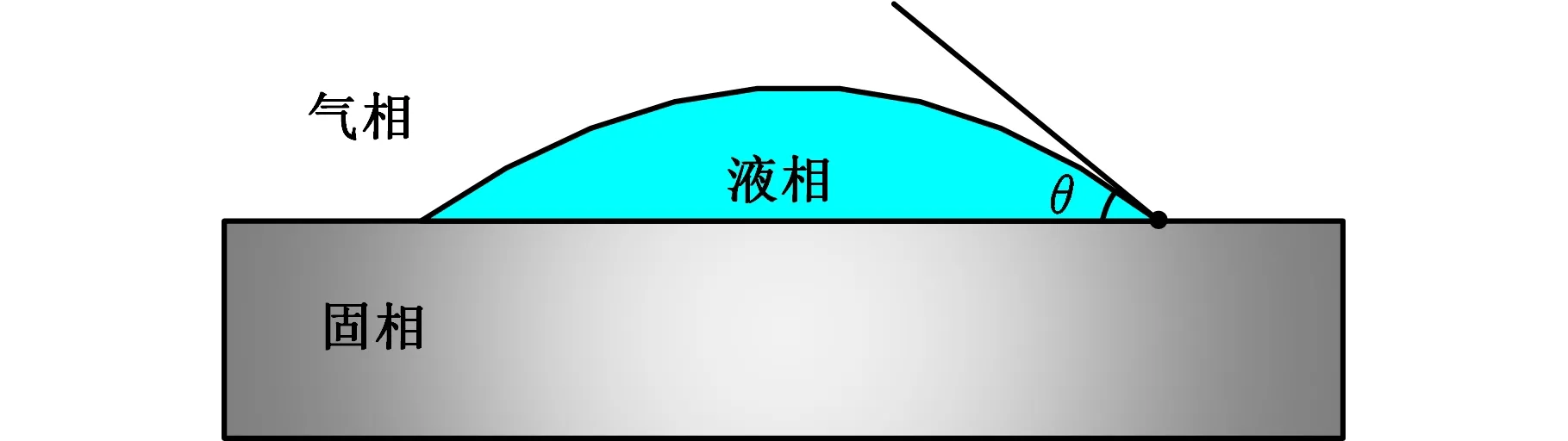
图8 接触角测量原理

图9 磨削温度测量方式
2.2 实验设计
在3种冷却方式下进行平面磨削,记录每个行程中的温度变化。磨削实验参数如表2所示。喷嘴出口出流体温度及气体流量如表3所示。每组实验前进行砂轮修整,以保证实验磨削条件相同。砂轮修整参数如表4所示。
2.3 实验材料
工件材料为Ti-6Al-4V,尺寸80 mm×20 mm×40 mm。基础油为上海金兆KS-1008合成脂。Al2O3纳米粒子兼具优良的润滑和摩擦学性能[22],因此选用体积分数为2%的Al2O3纳米粒子流体。表面活性剂十二烷基硫酸钠(SDS)加入纳米流体后,它在几乎不影响纳米流体摩擦性能的同时可以有效提高其分散与稳定性[23]。纳米流体的具体制备过程如下:①将体积分数2%的Al2O3纳米颗粒加入KS-1008合成脂基油,再加入体积分数0.1%的SDS分散剂。②用玻璃棒搅拌后,在超声振荡器中振动2 h,制备出具有高分散性能和高悬浮稳定性的纳米流体。
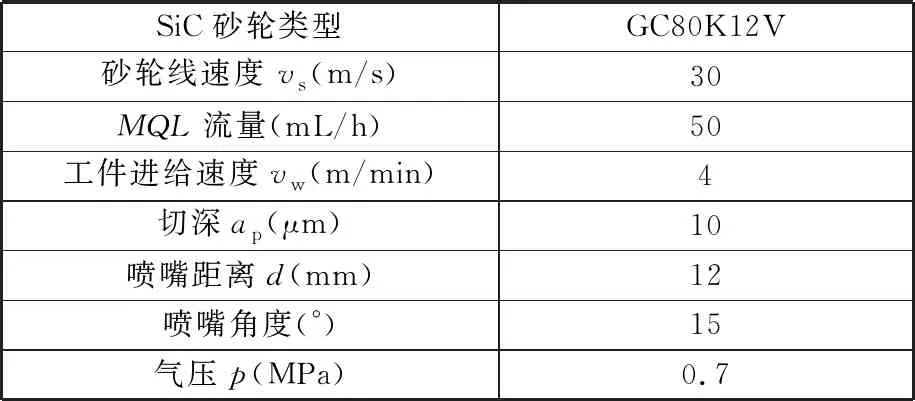
表2 磨削实验参数

表3 喷嘴出口出流体温度及气体流量

表4 砂轮修整参数
3 结果与讨论
3.1 工件表面温度
在3种冷却工况下进行连续磨削实验,并将10组顺磨进程温度曲线峰值作为工件表面的最高温度。低温风冷+纳米流体微量润滑的工件表面温度为155.9 ℃,比低温风冷的工件表面温度降低了41.6 ℃,降幅达21%;比纳米流体微量润滑的工件表面温度降低了58.2 ℃,降幅达27.2%。
3.2 仿真与实验结果对比
图10所示为3种冷却方式下的工件表面温度随时间变化的仿真结果。表5所示为工件表面温度仿真与实验结果,仿真与实验具有相同的变化趋势:砂轮磨削至测量点处时,工件表面温度急剧升高;砂轮离开该点后,工件温度缓慢降低,直至最终接近环境温度;仿真温度略高于实验温度,但误差小于5%。产生误差原因如下:模型假设进入工件的热量不与外界环境发生热交换,但在实验中,工件表面的热量不仅会在二维平面内进行热量传递,还有一部分通过工件的侧向向外传递;工件表面的热量还会分散至残余冷却介质及空气。
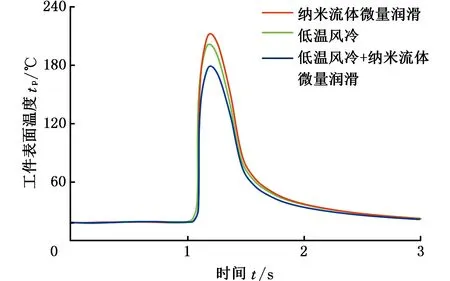
图10 工件表面温度随时间变化的仿真结果

表5 工件表面温度的仿真结果与实验结果
4 结论
(1)介绍了磨削区沸腾换热自然对流、核态沸腾、过渡沸腾和膜态沸腾的四个阶段的对流传热机理,建立了温度场有限差分模型。
(2)实验结果表明,低温风冷+纳米流体微量润滑的冷却效果最优,工件表面最高温度均值为155.9 ℃,分别比纳米流体微量润滑和低温风冷的工件表面温度下降了58.2 ℃和41.6 ℃。
(3)在数值模型的基础上对3种不同冷却条件下工件表面温度的变化进行了仿真分析,仿真与实验得到相同的规律。低温风冷+纳米流体微量润滑、低温风冷和纳米流体微量润滑三种冷却方式的工件表面最高温度相对误差分别为4.9%、4.2%和4.4%。

