摆线传动接触载荷与效率的关联模式及试验验证
宿月文 郭彩霞
宝鸡文理学院陕西省机器人关键零部件先进制造与评估省市共建重点试验室,宝鸡,721016
0 引言
摆线针轮传动具有较大的变速范围、较小的振动和噪声、高过载能力、结构紧凑等特点[1-2],被广泛用于减速电机和机器人关节减速器等领域。
近年来,针对摆线针轮传动的性能问题,国内外研究者围绕摆线针轮传动效率、多齿接触、齿廓修形、传动精度等问题进行了大量的研究。MACKIC等[3]研究了几何参数对摆线传动效率的影响,并对设计参数进行了优化。BLAGOJEVIC等[4-5]构建了单摆线轮的动力学模型,发现摆线轮和针齿的接触、摩擦对动力学性能有显著影响,其中摩擦对传动效率影响明显,而接触刚度和阻尼对动态特性有重大影响。GORLA等[6]研究新型摆线传动结构,并对传动效率进行了分析,发现在增加负载时,传动效率增加,即在高负载和高温情况下效率可达95%,其原因为高温导致润滑剂黏度下降,摩擦降低。ZHU等[7]认为轴承对摆线传动效率有影响,其计算结果显示考虑轴承时,传动效率会下降4%。SENSINGER[8]将摆线减速器效率与谐波和行星齿轮传动效率相比较,结果显示摆线减速器的效率更高。
摆线针轮传动具有多齿啮合接触的特点。MALHOTRA等[9]推导出摆线轮齿受力公式及传动效率,并讨论设计参数对接触应力的影响。TRAN等[10]研究了摆线轮与针齿的接触力和传动效率的理论公式,并以试验验证了传动效率的理论值。LITVIN等[11]提出齿面接触分析(TCA)理论,并计算运动误差。DO等[12]总结并对比了摆线齿轮传动的接触分析的几种方法,如TCA[13]、加载接触分析(LTCA)[14]、有限元分析(FEA)[15]、弹性多体系统(EMBS)[16]。其中,TCA方法无法很好地考虑轮齿的弯曲,EMBS方法使用少量模态的有限元模型和接触算法来模拟全弹性齿轮接触,具有较高的效率与精度。何卫东等[17]采用有限元法研究了摆线轮齿接触问题和时变啮合刚度。杨玉虎等[18]建立了考虑轴承刚度、轮齿啮合刚度及各构件弹性的有限元接触模型,分析了轴承刚度对摆线减速器整机扭转刚度的影响。XU[19]基于多体动力学和弹性接触理论提出了一种可精确预估摆线针齿动态啮合对数、确定接触点位置并获取接触载荷的动力学分析方法,可高效准确地完成齿廓修形和负载变化条件下的受载针齿数的预估及载荷计算。综上所述,摆线针轮传动的多齿啮合接触和传动效率的评估是摆线减速器传动设计与分析的关键问题。
为了揭示摆线针轮传动效率与设计、运行参数之间的关系,本文基于牛顿力学和弹性接触理论框架提出了一种摆线针轮传动效率理论模型。该模型通过负载反求摆线轮接触关系与载荷,并将传动效率描述为接触载荷的函数,最后通过专用的试验台对所提出的传动效率计算模型进行对比分析。
1 摆线轮动力学方程
摆线减速器如图1所示,主要包含4个部件,即输入轴、摆线轮、针齿销和输出轴。其运动原理如图2所示,O点为输入轴轴心,O1点为摆线轮中心,OO1为曲柄, 其长度为偏心距ec。输入轴为定轴转动,带动曲柄旋转并驱动摆线轮运动,摆线轮既绕O1点自转,又绕O点公转。因此,可定义OXY为固定坐标系,O1X1Y1为摆线轮坐标系。

图1 摆线减速器结构简图
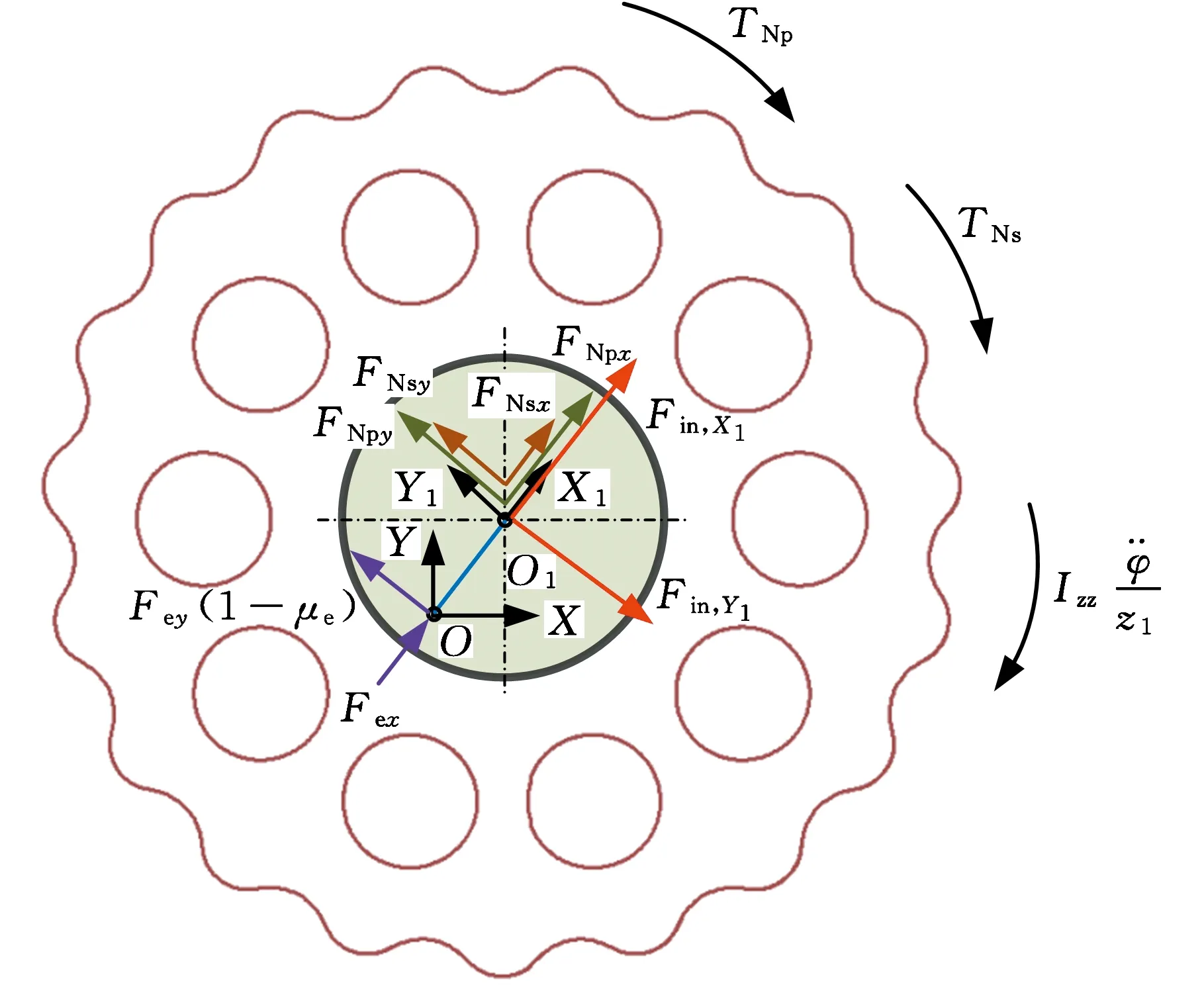
图2 摆线轮受力图
假定所有构件均为刚体,将轴承视为理想转动副。那么摆线轮质心的加速度:
aO1=aO+aO1/O,n+aO1/O,t
(1)
(2)
式中,aO为O点的加速度,由于定轴转动,因此aO=0;aO1/O,n、aO1/O,t分别为O1点在OXY坐标系下的法向加速度和切向加速度;φ为曲柄转角。
摆线轮的惯性力:
(3)
式中,mcy为摆线轮质量。
假定图2中FNpx和FNpy分别是摆线轮和针齿啮合力的合力在X、Y轴的分量;FNsx和FNsy分别是摆线轮和输出销轴的接触力的合力在X、Y轴的分量;Fex和Fey(1-μe)是输入轴与摆线轮之间的作用力,μe为轴承摩擦因数;TNp是摆线轮和针齿销作用力对O1点的合力矩;TNs是摆线轮和输出销轴的接触力对O1点的合力矩。则根据力平衡原理,得到
(4)
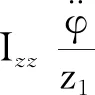
(5)
式中,Izz,os为输入轴转动惯量;z1为摆线轮齿数;TL为负载。

(6)
将式(6)的前三个方程重组并以矩阵形式表达如下:
(7)
根据式(7),有
(8)
另外,由输出端力矩平衡原理,得到输出力矩等于负载,即
Tout=TL=TNs
(9)
摆线轮的输入力矩Tin可表示为
Tin=Fey(1-μe)ec
(10)
综合式(8)和式(10)得
(11)
假定ωin和ωout分别为减速器输入、输出角速度,那么减速器的瞬时传动效率可表示为
(12)
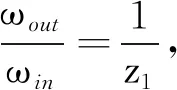
(13)
考虑到减速器的输入速度和输出负载是给定的,通过求解摆线轮与针齿以及输出销轴的接触载荷,即可得到减速器的瞬时功率。
2 摆线轮接触载荷计算
2.1 摆线传动的几何模型
摆线轮齿廓的精度对传动性能有重要影响。为了补偿误差、改善润滑,常常对标准摆线齿廓进行修形以形成必要的齿隙。常见的修形方法有等距修形、移距修形和转角修形法。综合上述三种修形方法,可得到通用的摆线轮齿廓[20]。
如图3所示,摆线轮齿廓上任一点在其自身坐标系O1X1Y1下的参数化坐标表达为rgc=(xgc,ygc,0,1)T,其中,
(14)
(15)
式中,Rz为针齿分布圆半径;rz为针齿半径;iH=Nb/Ng,Nb为针齿数,Ng为摆线轮齿数;φ为啮合相位转角;ΔRz为移距修形量;Δrz为等距修形量;Δδ为转角修形量。
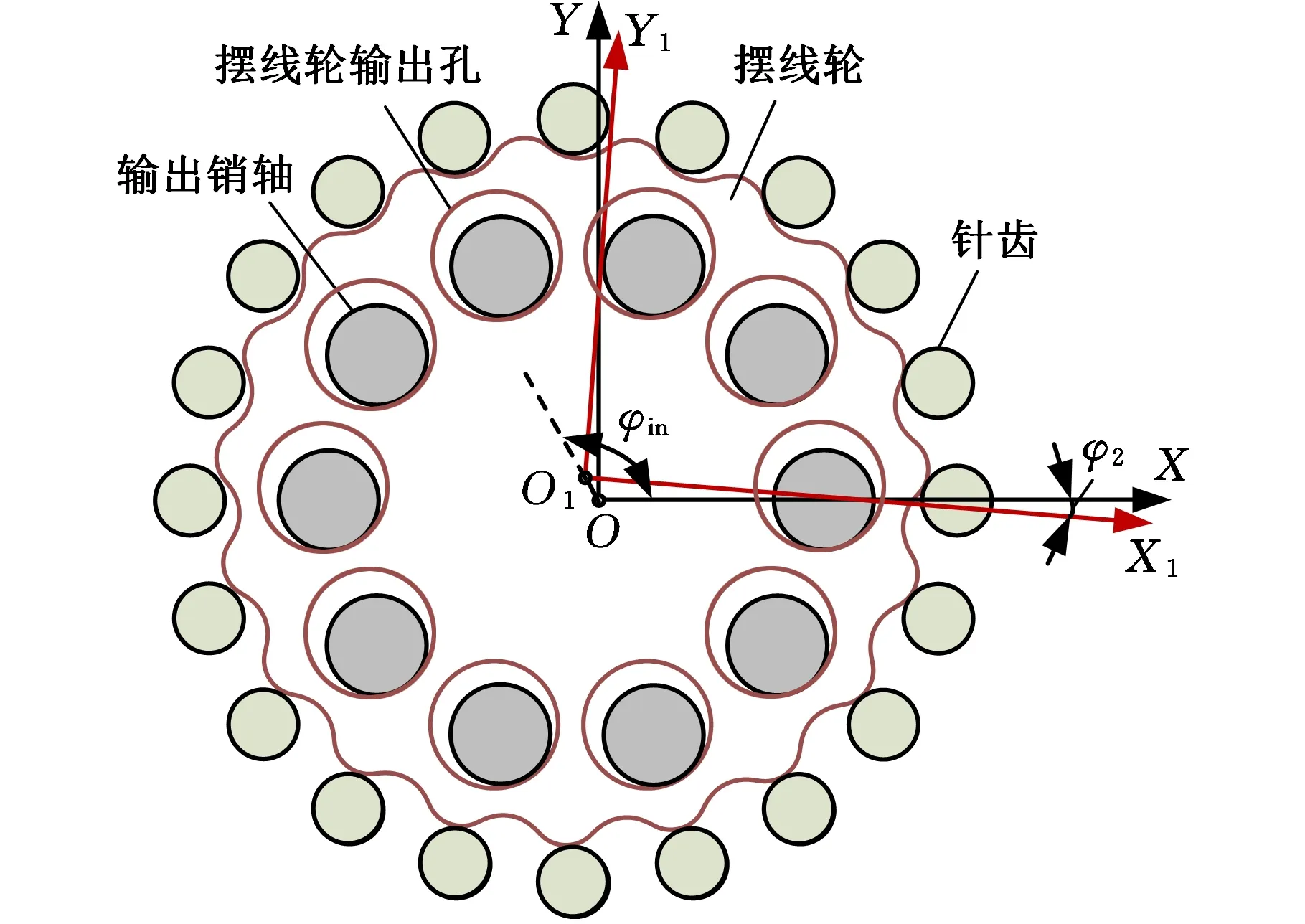
图3 单级摆线传动机构几何模型
齿廓上任一点的外法向矢量:
(16)
由于针齿固定,则在固定坐标系OXY下针齿几何位置可表达为
(17)
式中,Rp为针齿分布圆半径;rp为针齿半径;Np为针齿数;i为针齿的位置序号。
针齿表面任一点的外法向矢量:
(18)
2.2 摆线传动的接触位置判定
2.2.1摆线轮与针齿的接触判定
为了实现摆线轮与针齿及输出机构销轴的接触判定,需要将摆线轮齿廓和输出孔的坐标转换到固定坐标系下。设定坐标系Sc相对于Sf的转角为φ2,则摆线轮平面运动所对应的平移旋转复合坐标转换矩阵:
(19)
式中,φ2为摆线轮转角;φin为曲柄转角。
那么在固定坐标系下的摆线轮齿廓方程:
gcf=Tfcrgc
(20)
同理,将原摆线轮坐标系下摆线轮齿廓任一点法矢量ngc,经坐标变换得到固定坐标系下的相应法向矢量:
ngf=Tfcngc
(21)
摆线轮齿廓与针齿的接触需满足:①两个齿面接触点坐标相等;②两个齿面接触点的法向量相等。接触条件的数学表述为
rpf(β)=gcf(φ,φ2,φin)
(22)
npf(β)=ncf(φ,φ2,φin)
(23)
式(22)和式(23)中,φin为已知曲柄转角;φ、φ2、β为未知量。由式(22)可得到关于X、Y坐标的2个方程,加上式(23)共3个方程。求解这3个方程即可得到3个未知变量,进而确定接触点初始位置。
2.2.2摆线轮与输出机构销轴的接触判定
摆线轮上输出孔的中心在坐标系XcYcZc下的几何位置参数化表达如下:
(24)
式中,Rs为摆线轮上输出孔分布圆半径;Ns为输出孔(销轴)数;j为各孔的位置序号。
将其转化到固定坐标系下:
rsf=Tfcrsc
(25)
输出机构旋转轴与固定坐标系相同,因此,输出机构上销轴的中心位置为
(26)
式中,Rso为摆线机构销轴分布圆半径。
输出机构销轴与摆线轮孔的接触可通过圆柱内接触的形式来表达,即针对每一对销轴与孔,其接触状态的判定依据如下:
|rsof-rsf|≤|rsc-rso|
(27)
式中,rsc为摆线轮输出孔的半径;rso为输出机构销轴的半径。
2.3 摆线轮载荷分析
摆线针轮传动中,摆线轮齿与针齿的啮合属于多齿啮合,且不同齿的接触位置与接触载荷不同。假定啮合点接触可简化为两圆柱外接触,则接触力可表示为[21]
(28)
(29)
式中,δNpi为接触变形;E*为复合弹性模量;B为摆线轮宽度;Rcq为摆线轮接触点处等效曲率半径。
由图4可知,接触变形δNpi表示为
δNpi=rz-|rpi-gcf|
(30)
式中,rpi为接触针齿的位置矢量。
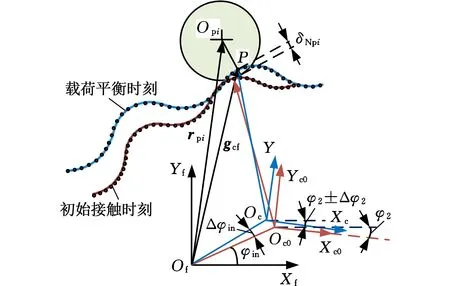
图4 摆线轮-针齿的接触变形分析
此外,摆线轮与输出机构销轴的接触属于圆柱内接触,其接触力与接触变形的关系[22]如下:
(31)
ΔR=rco-rso
式中,rco为摆线轮输出孔半径;δNsi为接触变形量。
由图5可知,接触变形δNsi表示为
δNsi=|rsc-rso|-|rsof-rsf|
(32)

图5 摆线轮-输出销轴的接触变形分析
2.4 摆线轮接触载荷的确定
由2.2节和2.3节可得到接触点初始位置,以及接触变形和接触力的关系。在给定负载的前提下,根据静力平衡原理,以φ2为基础并叠加微小变化量Δφ2,通过反复微调摆线轮转角φ2±Δφ2,以及摆线轮中心位置,以得到新的接触点位置和接触载荷,最终得到给定负载TL作用下的所有接触载荷的准确分布。具体流程见图6。

图6 摆线轮接触载荷分布的确定方法
假定Nbc为处于接触的针齿数,若Nb为偶数,则Nbc=Nb/2;若Nb为奇数,则Nbc= (Nb-1)/2。根据各接触针齿作用力,可得到任一时刻针齿对摆线轮的合力在X、Y方向的分量:
(33)

此外,单个针齿对摆线轮的接触力对其质心的等效力矩:
(34)
式中,diy、dix分别为第i个针齿力在X、Y方向的力臂。
所有针齿对摆线轮的接触力等效力矩之和:
(35)
假定Nsc为处于接触的销轴数,若输出销轴总数Ns为偶数,则Nsc=Ns/2;若Ns为奇数,则Nsc= (Ns-1) /2。进而可得到输出摆线轮输出孔和输出机构销轴的合力:
(36)
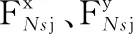
任一配对的摆线轮输出孔与输出销轴之间的接触力对其摆线轮质心的等效力矩为
(37)
式中,djy、djx分别为第j个针齿力在X、Y方向的力臂。
则所有对摆线轮的接触力等效力矩之和:
(38)
基于图6所示的流程,可得到任意时刻摆线轮的接触载荷分布(图7),以及曲柄转角φ′in和摆线轮自转角φ′2。
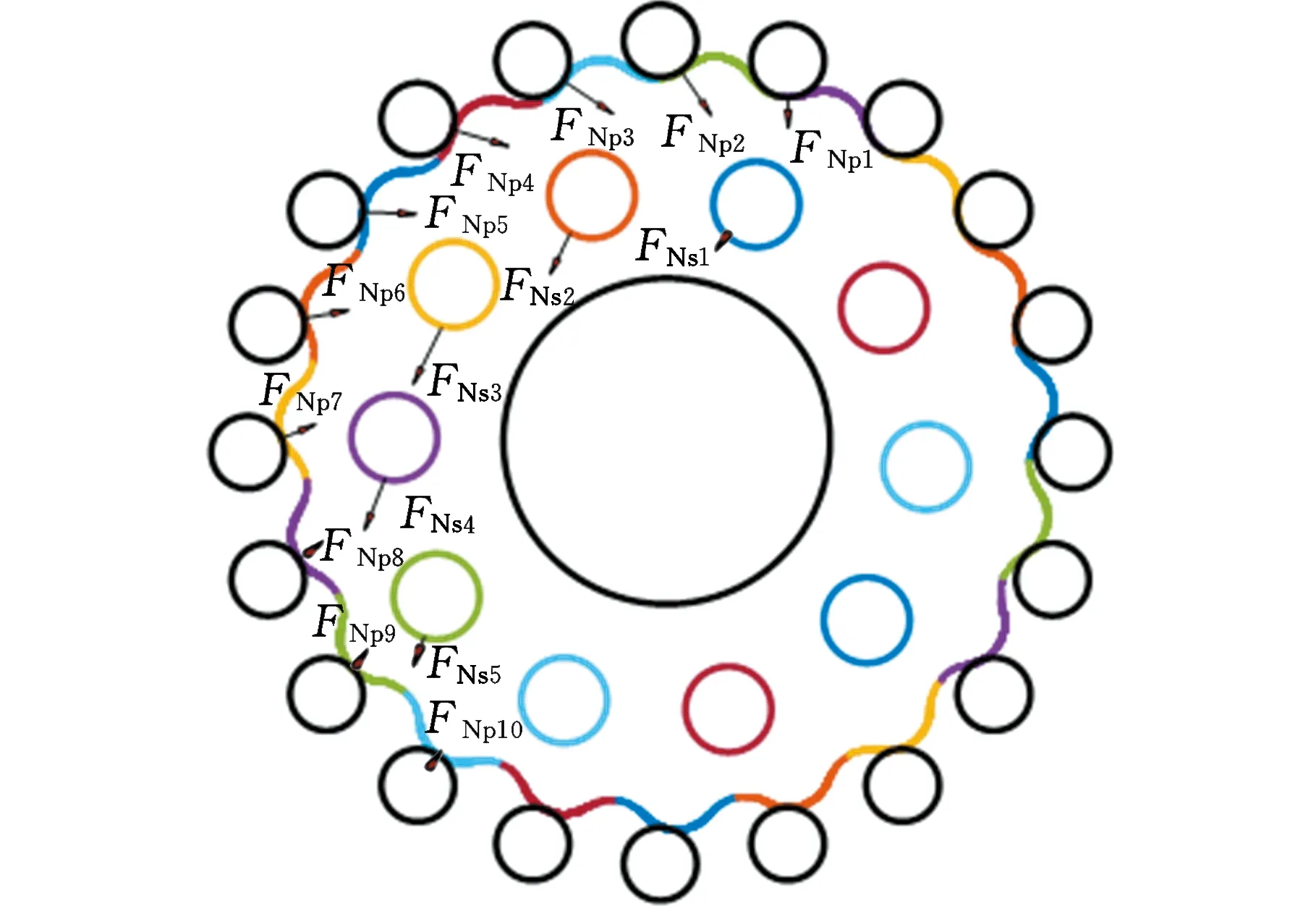
图7 不同时刻的摆线轮接触载荷分布
3 单级摆线传动性能分析
3.1 传动性能分析模型的参数设置
基于上述方法,以某一摆线针轮传动系统为例,建立该类系统的刚体接触多体动力学模型。模型中,针轮上均匀分布20个针齿。摆线轮在曲柄轴驱动下以及受针摆接触作用后将产生公转和自转运动。摆线针轮传动系统的几何结构参数见表1。
传动效率和振动是摆线针轮减速器的重要性能。传动效率是功率损耗评估、功率密度设计和摩擦学设计的重要参数,而转矩、转速的波动导致振动噪声加剧,传动精度降低。本文根据式(11)和式(13)计算输入力矩和传动效率,并将其作为主要参数来评估加速器性能。图8与图9分别为输入转速为1000 r/min时的输入力矩Tin、输出转速ωout(ωout=dφ′2/dt)随时间变化的情况。
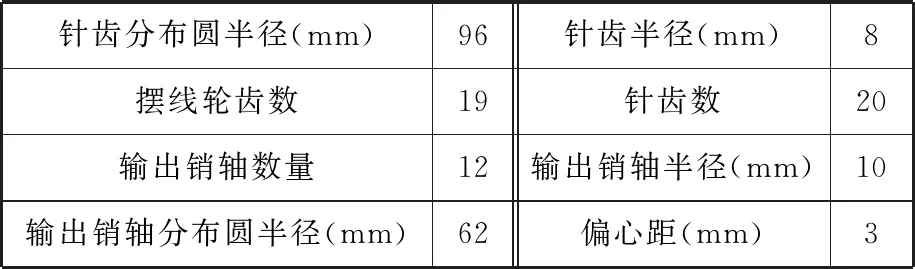
表1 摆线针轮机构主要结构参数
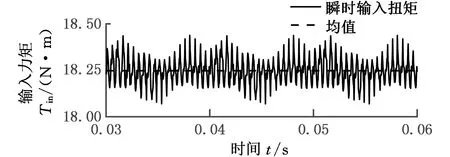
图8 输入力矩变化情况
以图8所示的力矩的波动情况为指标进行振动特性分析,定义输入力矩对均值的最大偏移量作为考察指标,即
(39)
其中,Tin(t)是来自仿真的输入力矩的瞬时值。同时,引入傅里叶变换以考察输入力矩对均值的偏移量的频域特性,即最大振动频率对应的最大偏移量:
(40)
式中,F(·)表示傅里叶变换。
下文将基于本文所提方法以及给定设计参数,针对不同的针齿半径、摆线轮齿数及输出销轴数量对传动特性的影响进行分析。
3.2 针齿半径对传动特性的影响
由图10可见,针齿半径越大,摆线传动效率越高。同时,针齿半径增大会导致扭矩非周期性和谐波比增大,但是其影响并不显著。工程实际中,针齿半径增大将导致总体结构尺寸增大。
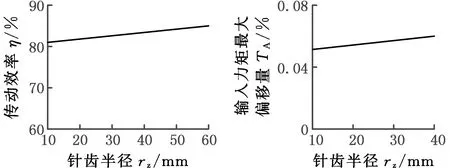
(a)传动效率(b)输入力矩最大偏移量
3.3 摆线轮齿数对传动特性的影响
图11所示为摆线轮齿数变化对传动特性的影响。摆线轮齿数越大,传动效率越高,而扭矩非周期性和谐波比随着齿数增大而下降。摆线轮齿数的变化不仅影响自身几何尺寸,还可导致减速器减速比的变化。

(a)传动效率(b)输入力矩最大偏移量
3.4 输出销轴数量对传动特性的影响
图12所示为输出销轴数量对传动特性的影响。可见,当输出销轴数量大于5时,传动效率大体上不再随输出销轴数量的变化而变化;同时,扭矩非周期性和谐波率基本保持恒定,且处于较低的水平。减速器具有更多输出销轴数时,可以更有效地分配传动力,使得输出力矩更为均匀。相反,设计较少的输出销轴,将无法有效实现负载的平均分配,导致机构振动的增大和效率的降低。
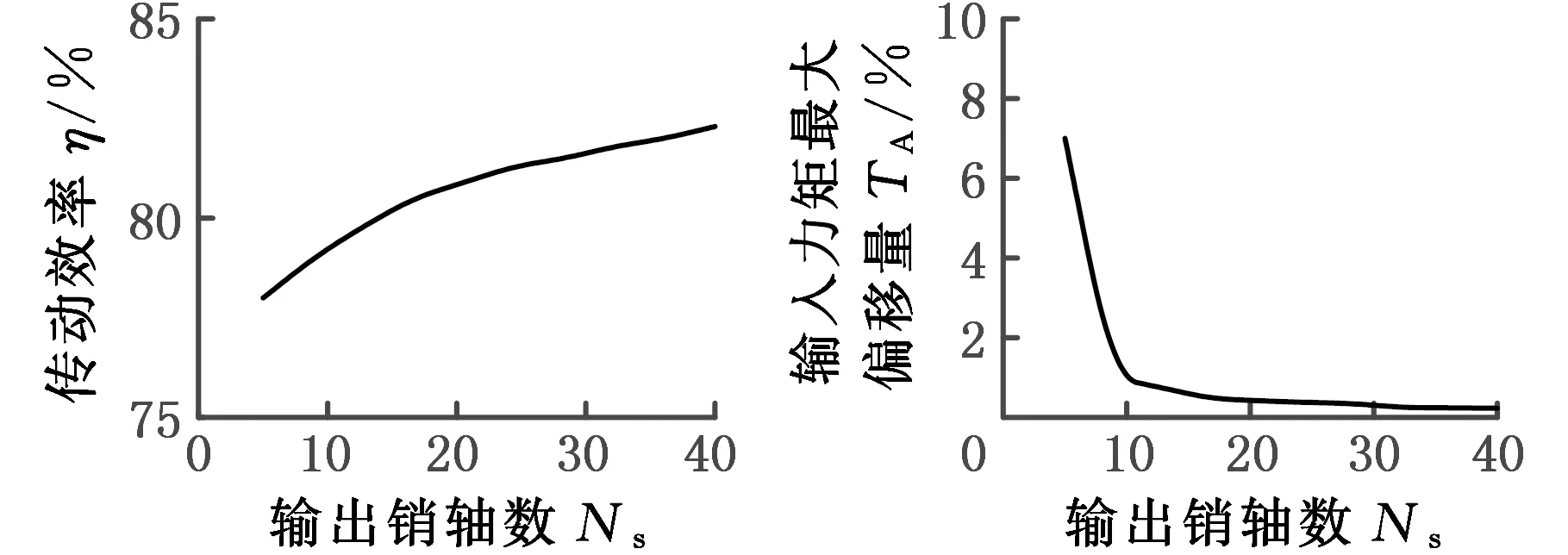
(a)传动效率(b)输入力矩最大偏移量
4 试验方法
4.1 试验台构成
摆线针轮减速器试验基于一体化设计的专业测试装置进行,该装置满足输出功率不超过1.8 kW、输出转矩不超过1000 N·m、额定转速1500 r/min、最高转速不超过3000 r/min的减速机效率测试。为满足不同类型减速器效率试验,减速器安装采用固定底座+安装盘方式,更换方便;试验台架加载采用伺服加载电机作为负载,负载可以任意调节。
图13为试验台架整体图。主轴方向由左至右依次为驱动伺服、轴承座、输入端扭矩转速传感器、轴承座、被测减速器、后端轴承座、后端扭矩转速传感器、轴承座、增速器和加载电机。

图13 专用试验台
4.2 试验台运行结果与理论对比
在被测减速器的输出轴上加载恒定扭矩进行测试,从0增加到既定速度1000 r/min并保持恒定20 s,然后再次降至0,在这20 s内获得的扭矩和速度值取平均值。根据式(12)计算即时效率。
图14显示了不同负载情况下传动效率的理论计算值和测试值。由图可见,理论模型得到的传动效率不随着负载的增加而变化,且只在较大负载的情况下理论值才与测试值接近。观察测试值可发现,传动效率数据存在两个区域,即负载较小时(小于150 N·m),传动效率变化幅度相当大;而在负载较大时,随着负载的增加,传动效率变化较为缓慢,此时效率值已逼近饱和值。
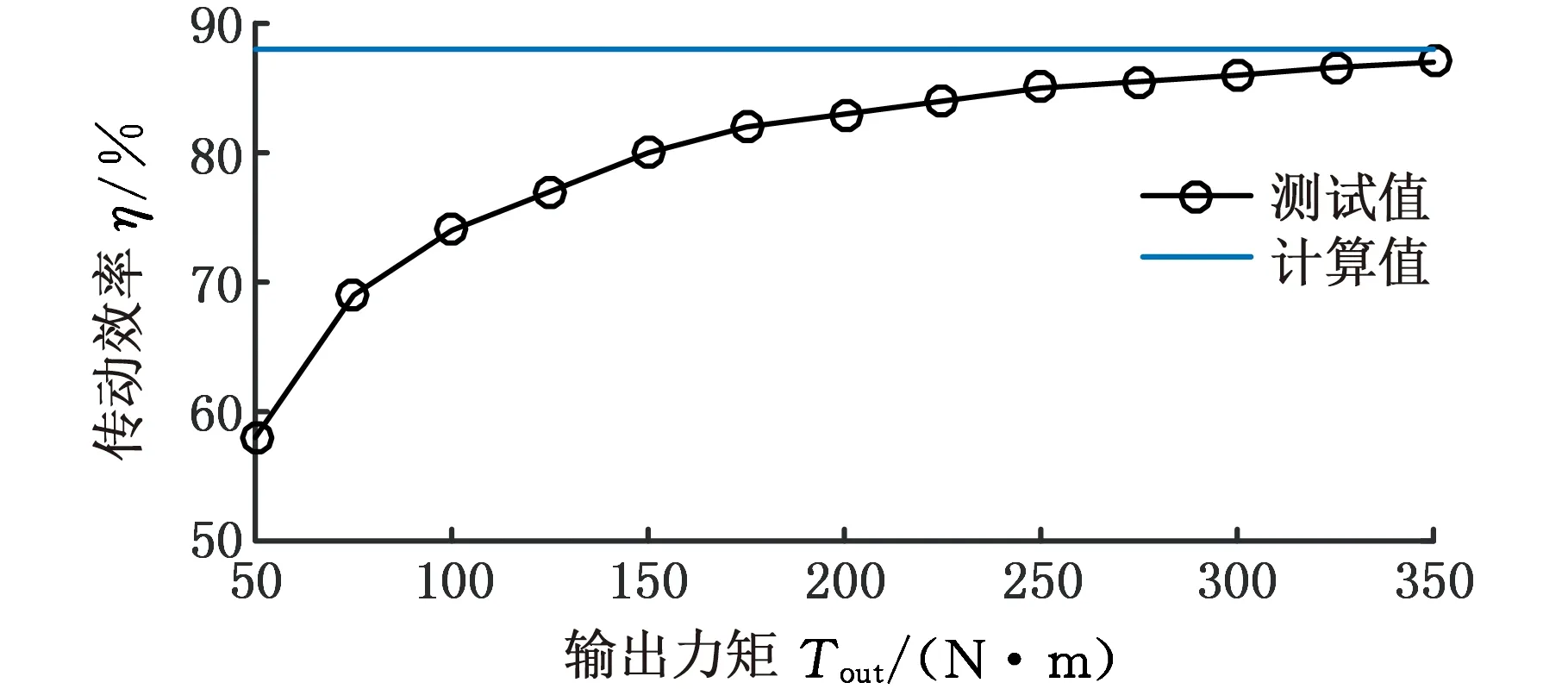
图14 传动效率的理论计算值和测试值(ωin=1000 r/min)
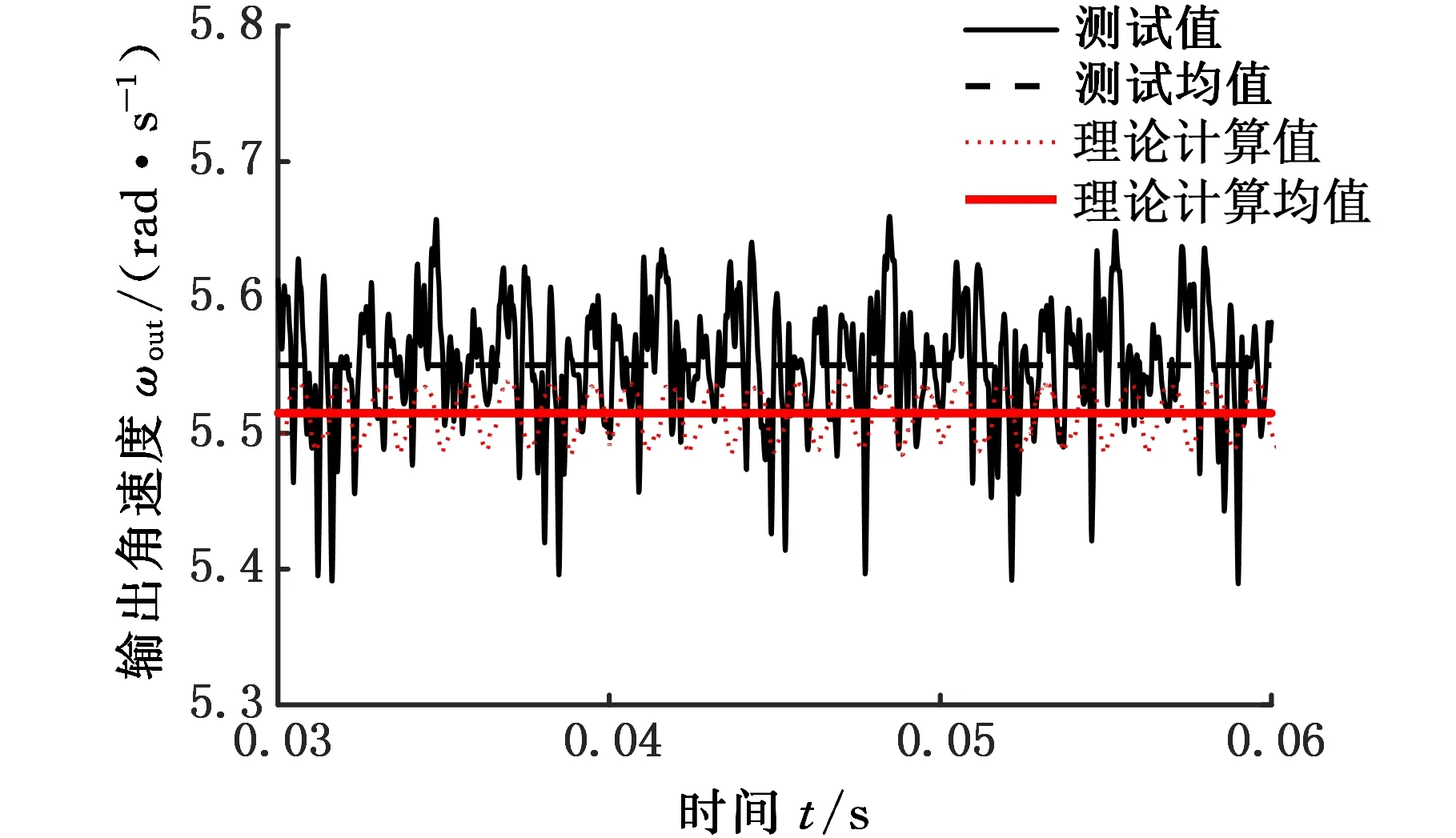
(a)Tout =70 N·m

(a)Tout =70 N·m
为了进一步分析所提方法在不同负载时表现的差异性,由传动效率理论计算式(12)可知,在负载和输入转速给定的情况下,理论效率主要受输出转速和输入力矩影响。图15显示了负载为70 N·m和300 N·m时的输出转速,两种情况下其理论均值和测试均值无明显差异。图16显示了对应两种负载时的输入力矩,在负载为70 N·m时,其理论均值显著低于测试均值,而在负载为300 N·m时,其理论均值与测试均值差异很小。可见在低负载时,输入力矩的理论值显著低于测试值,导致此时的理论效率高于测试效率。
因此,理论模型存在缺陷,即仅在高负载情况下是有效的。这可能是因为理论模型忽略了摆线轮轴承的摩擦效应,即理论模型未考虑摩擦力矩,导致其计算输入力矩值偏低,未考虑轴承摩擦功耗,导致其理论效率偏高。由于摆线传动功率损耗主要由于针齿与摆线轮齿的啮合摩擦,高负载时轴承功耗占比较小,故理论效率与测试效率接近;在低负载时,轴承功耗占比相对较高,不可忽略,导致理论效率与测试效率差异明显。
5 结论
(1)针对单级摆线减速器,基于牛顿法和接触力学,提出了一种简明的瞬时传动效率计算方法,即以任一时刻摆线轮接触分析获取其所受接触载荷的合力和合力矩来描述传动效率,并通过试验对该方法进行了验证。
(2)理论计算结果表明,传动效率不随负载变化而变化。但是试验结果表明,负载较低时,传动效率偏低,随负载增大而快速上升;负载较高时,传动效率变化不大,趋于稳定值。理论传动效率与测试值在高负载时差异不大,但在低负载时差异明显,其原因为输入力矩的理论值显著低于测试值,导致此时的理论效率高于测试效率。
(3)所提方法在低负载时误差明显,在高负载时与测试值较为接近,其主要原因为该方法未考虑摆线轮轴承的摩擦效应,如摩擦力与摩擦力矩。由于针齿与摆线轮齿的啮合摩擦是主要功率损耗原因,高负载时轴承功耗占比较小,故理论效率与测试效率接近;在低负载时,轴承功耗占比相对较高,不可忽略,导致理论效率与测试效率差异明显。
(4)研究中忽略了轴承润滑、摩擦及动力学效应,后续研究必须详细构建考虑轴承环节的动力学模型,建立完备的摆线针轮传动效率评估模型,以实现对传动效率和振动特性的准确计算。

